自动控制原理课程中描述函数法的教学探讨

余 洁

（上海电力大学自动化工程学院 上海 200434）

“自动控制原理”课程是自动化专业、电类相关专业的专业基础课，是学好后续专业课程的重要基础。“自动控制原理”的控制系统包括线性控制系统及非线性控制系统。实际的系统没有纯粹的线性系统，组成控制系统的元件其静态特性都有着不同程度的非线性。因此，掌握非线性系统分析方法是相当重要的。“自动控制原理”中非线性控制系统的内容主要包括:典型非线性特性，描述函数分析方法和相平面析法，利用非线性改善系统性能等。其中描述函数法计算复杂，常被学生反映理解、掌握困难。本文作者根据自己一线教师的教学实践，在本篇论文中探讨了新的教学策略。

一、描述函数法

描述函数法是分析非线性系统的一种近似方法，是频率法在非线性系统分析中的推广[1]。其思想是用谐波分析的方法，忽略由于对象非线性因素所造成的高次谐波成分，而仅使用一次谐波（基波）分量来近似描述系统特性。

（一）基本原理

假设非线性系统的结构图如图1所示，图中N及G(s)为非线性元件模型及线性部分的传递函数，r(t)，y(t)为系统的激励及响应。x1(t)，x2(t)为非线性元件的输入输出。

图1

假设非线性系统满足如下条件：

①非线性元件N不是储能元件；

②非线性元件N的非线性特性是斜对称的，f(x1(t))=-f(x1(t))。

③系统的线性部分具有较好的低通滤波器性能，当非线性元件输入正弦信号x1(t)=Asinωt时，系统的响应x2(t)的高次谐波在通过线性部分后将大大衰减，输出信号可近似认为只有基波分量。

根据上述假设条件，x2(t)仅考虑基波部分

仿照幅相频率特性的定义 ，建立非线性特性的描述函数.其数学表达式为

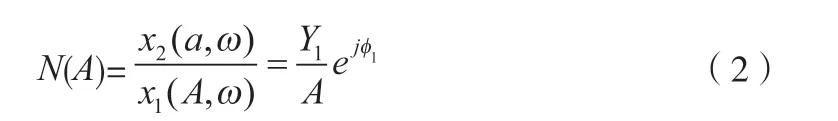
式中:N(A)——非线性部分的描述函数；A——非线性部分正弦输入信号的振幅；Y1——非线性部分输出信号中基波分量的振幅；φ1——输出信号中基波相对正弦输入信号的相位移；A1——基波中余弦分量的振幅；B1——基波中正弦分量的振幅；

（二）描述函数进行稳定性分析

非线性控制系统图1所示。图中非线性元件的描述函数为N(A)，则非线性系统的闭环频率响应可近似的写为：

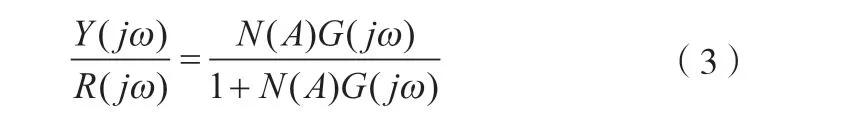
由式（3）可以求得非线性系统的特性方程为

即

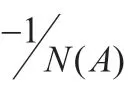
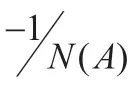
图2

二、教学方法的探讨

为了使学生能够理解和掌握描述函数法，课堂教学应从几个方面进行改进。

（一）教学过程将仿真与理论相结合

结合Matlab验证相关理论有助于培养学生“眼见为实”的科学精神。仿真包括负倒描述函数曲线及线性部分奈奎斯特曲线的绘制，自激振荡的验证两个方面。以下用一个案例进行阐述。

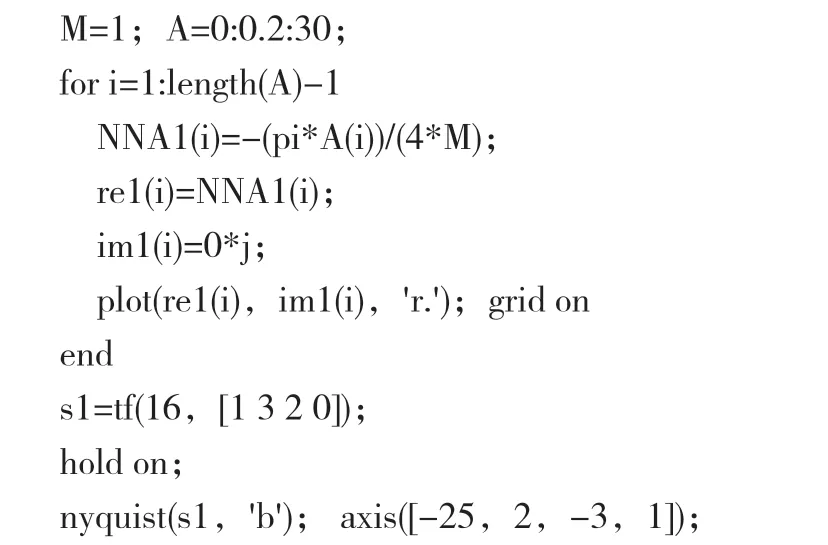
得出结论，存在相交情况，为稳定的自激振荡；

②调节线性部分的开环根增益K=32，分析K对自激振荡的振幅及频率的影响，如图3。由图可知，系统2（K=32）时，自激振荡的频率不变，但是振幅会增加一倍。

图3 自激振荡的判定

③在SIMULINK环境中，搭建系统框图[4]，完成自激振荡频率及振幅的判断。图4为系统1（K=16）的仿真框图，参数设置和结果。

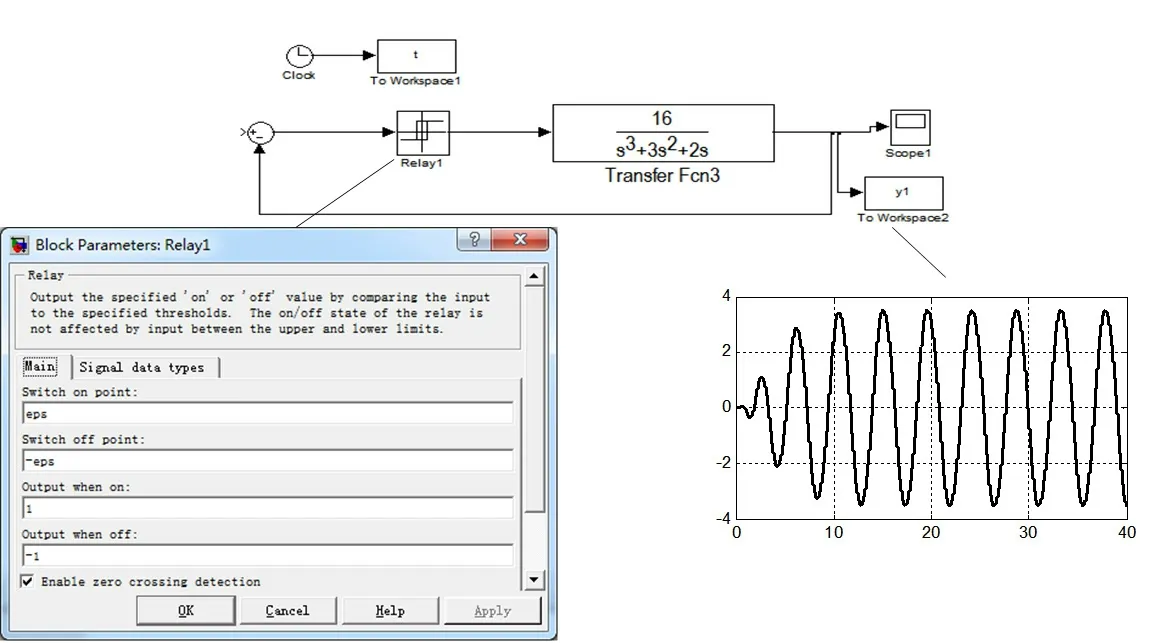
图4 SIMULINK验证框图

采用上述的教学方法，学生易于理解，理解的更为深入。

（二）引入复杂工程案例，培养学生解决工程实际问题的能力

教学过程应紧密围绕以学生为中心，以毕业要求为导向的OBE理念，结合电力系统及控制系统中的复杂工程案例，加强知识点与工程应用的有机联系，培养学生运用基本理论解决工程实际问题的能力。在教学实践中，作者以张绍和等发表的“用描述函数分析多机电力系统静态稳定的一种方法”及廖幻年等发表的“基于描述函数法的滚动通道自持振荡研究”[5]两篇论文涉及的工程案例展开案例教学，提出问题引发讨论，展开如何结合描述函数法的概念解决复杂工程问题的启发性教学，为学生利用描述函数法解决实际问题提供思路，构建基本框架。

实践表明，结合工程案例，对教学中涉及的概念、性质及理论的运用从工程化的角度进行分析和阐述，对提高学生的分析问题、解决问题的能力都有极大的帮助，也能提高学习的乐趣，达到学以致用的目的。

（三）将“课程思政”融入教学，激发学生积极向上的学习热情和爱国情怀

在“描述函数法”课程教学中应融入思想政治教育，以“坚持立德树人”为根本任务，用好课堂主渠道，向学生传递严谨专业的科学精神以及敬业奉献的职业精神。

首先，非线性系统不满足叠加定理，稳定性除与系统的结构形式和参数有关外，还与外作用及初始条件有关。对于相同结构和参数的非线性控制系统，运动的最终状态可以完全不同。这都造成了非线性系统稳定性判定的困难。描述函数法的提出是基于一定条件下的简化分析方法，教学中启发学生，对于学习、生活要讲究方式方法，常规方法不行就换个角度，不要一条道走到黑，换一个角度解决问题，或许会柳暗花明。

其次，描述函数法判定系统的稳定性时，负倒描述函数曲线可以看作是判定稳定的边界。从这一角度启发学生，凡事都有底线，做事做人应遵循原则、守住底线，要做一名具备道德意识、法律意识，遵守社会公德，遵守行业的标准、规范的接班人。

同时，结合描述函数法在电力系统中的应用进行引导教育，引导学生应当多关注国家能源政策的发展动向及发展趋势，为今后从事电力相关科学研究储备关键技术，为国家能源的未来发展做出自己的贡献。

三、结论

本文针对描述函数法的课堂教学提出了教学改进方法，并给出了较为具体的教学实施策略。在教学实践中通过采用以上教学方法，促进学生对知识点的融会贯通，提高课程的教学质量。