分析化学“去公式化”新课程体系
邵利民
中国科学技术大学化学系,合肥 230026
理、工、农、医、师范类高校中,分析化学(定量化学分析部分)是多个专业都会开设的一门基础课。这些专业包括化学、化工、材料、环境、食品、生物、医学、药学、地学等,也从一个侧面反映了该课程的重要性。
从课程内容看,分析化学包括定量化学分析和仪器分析。大多数国内高校中,这两部分内容分别设课,课程名多为“分析化学”和“仪器分析”,或者“分析化学I”和“分析化学II”。本文探讨定量化学分析部分,仍然采用“分析化学”这一名称,既是遵循惯例,也是便于叙述和理解。
分析化学课程的主要内容是化学平衡的定量解析,以及在此基础上建立的滴定分析方法。课程包含较多的滴定分析内容,然而并不意味着课程旨在介绍滴定分析技术,实因滴定分析是化学平衡定量解析知识的绝好载体。
分析化学课程具有鲜明特色,是“四大化学”之一的重要基础课。大学基础课不仅介绍特定知识,更重要的是帮助学生建立科学思维方式和培养逻辑推理能力。然而,分析化学传统课程体系却偏离了这种目标,并随计算机技术的快速发展而日益严重。
1 传统课程体系的特点和局限性
分析化学传统课程体系具有悠久的历史,而且明显受到早期计算工具的限制。计算工具的影响甚至左右了传统课程体系的问题求解思路和策略。
传统课程体系包含大量的、简单的计算公式。只要记住这些公式,使用普通工具就能够完成运算,这一特点可概括为“记忆换运算”。公式推导过程中引入近似手段,以获得简单形式,这一特点可概括为“近似换简化”。为了控制近似手段导致的误差,引入适用条件以限制公式的适用范围,但是也进一步加重了记忆负担。
通过“记忆换运算”和“近似换简化”,传统课程体系成功克服计算困难,并将误差控制在允许范围之内。这在计算工具欠发达年代是一个巨大成就。但是,曾经的计算困难在当前发达的计算技术面前已经不复存在。当计算不再困难,传统课程体系的优势就渐失支撑,缺点则愈发明显,并且有三个层级的表现。
在第一层级,传统课程体系的缺点影响了学与教的积极性。学生感受最直接、反映最强烈的是记忆负担过重;尤其当他们意识到计算可以方便地通过软件完成、大量记忆付出不再必要时,学习积极性就更为受挫。对于教师,诸多公式的介绍和推导占用了本不富裕的课时,而这些课时的必要性难以得到有效支撑(因为计算确实不再困难)。传统体系也限制了教学研究思路。很多教研的目标仍然是推导出公式,结果是:通用的公式很复杂,简单的公式不通用,陷入难以走出的困境。
在第二层级,传统课程体系的缺点导致学生对课程的误解。大量的简单公式是为了解决计算困难,这是技术措施的特征;公式推导时引入的近似手段缺乏通用性,在某些情况下失效,这是技术措施的特征;复杂问题因为没公式可用而无法解决,这仍然是技术措施的特征。可见,传统课程体系凸显了分析化学的技术性,使学生误认为分析化学仍然是一种技术,而非科学。分析化学当然是一门科学,具有完整、自洽的理论,只是大量公式割裂了化学平衡理论的内在统一性,错误地暗示了理论的不完善。对于实用性技术,如果不再出现需求,它就失去发展动力,甚至可能被取代。科学则不同,不以实用为目的,自然就没有“过时”“无用”之说。
在第三层级,传统课程体系的缺点不利于学生培养科学思维。大量公式将学习重点集中在问题的求解层面而非分析层面。按图索骥式的公式套用尽管方便,却降低了深入探索的必要性。如果探索环节得不到加强,那么学生主动思考、刻意训练的积极性就会下降。另外,传统体系极其倚重近似手段,在获得简单算式的同时,也传递这样一种理念:对于复杂问题,不按照一般思路抽丝剥茧,而是通过近似处理,将之简化为一个较简单的问题,最终得到近似结果。近似手段是一种捷径,捷径虽然有用,但不是解决科学问题时的首选。低年级本科生的科学思维方式还未成熟,此时强调近似手段,不利于他们的发展。
传统课程体系中的近似手段其实很简单——推导时忽略某些很小的项(以简化计算),但是很难运用,因为很小的项并不意味着它对最终结果的影响一定小。这种影响需要通过误差传递来研究,而误差传递比较繁琐,所以人们一般通过实例进行验证。近似值的验证往往需要与准确值比较;既有准确值,而且得到准确值目前并不困难,那么近似值便失去价值,近似手段似乎成了屠龙之技。
综上所述,分析化学传统课程体系的突出问题不在于化学平衡知识,而是过时的解决策略和计算方法。因此,教学改革不能固守传统体系、删减课程内容,而应当建立不依赖公式的新课程体系。
2 “去公式化”课程体系的理论框架
多年来,我们致力于分析化学课程改革,对化学平衡进行了系统深入的研究,最终提出“去公式化”新课程体系。新体系中,化学平衡和滴定分析的各类计算均可以按照一个统一模式来完成,这就是图1所示的理论框架。

图1 “去公式化”课程体系的理论框架
理论框架通过I、II两步实现“去公式”,因为不同类型的问题都遵循相同的基本等量关系;通过II、III两步实现“去近似”,因为推导过程中不再使用近似手段。
分析化学课程中各类问题的求解思路,都可以纳入这个理论框架。例如,溶液组分浓度的“去公式化”计算、滴定终点误差的“去公式化”计算、滴定曲线的“去公式化”绘制、准确滴定判别的“去公式化”实现。
3 化学平衡定量解析中的等量关系
图1中的理论框架表明,等量关系在化学平衡定量解析中扮演极其重要的角色。分析化学教材中,常见三种等量关系,分别是物料平衡式(material balance equation,MBE)、电荷平衡式(charge balance equation,CBE)和质子平衡式(proton balance equation,PBE)。
这些等量关系是化学平衡定量性质的数学描述,也是定量解析的着手点;作为化学平衡与数值计算的纽带,其重要性不言而喻。如果不明确这些等量关系的独立性,那么求解效率不仅会降低,定量解析的理论结构也有失清晰。
CBE被证明不独立于MBE[1]。PBE可以由MBE结合CBE推导出,也不是一个独立条件[2]。CBE和PBE都不是独立条件,所以在化学平衡定量解析中并非必须。换言之,MBE是化学平衡定量解析的独立等量关系。
MBE足以完成酸碱、配位、氧化还原和沉淀四大平衡的定量解析,但是CBE在酸碱平衡解析中更具优势[1]。由此得到等量关系的使用原则:1) 首选MBE;2) 涉及酸碱平衡时使用CBE;3) 不推荐使用PBE。
绝大多数分析化学教材使用质子平衡式PBE处理酸碱平衡,但是我们不推荐。列出等量关系是解题中间步骤,应该直观、简单而且不易出错,PBE在这些方面逊色于CBE,对初学者而言尤其如此。此外,不推荐PBE并不意味着舍弃酸碱质子理论,因为PBE只是酸碱质子理论的一个推论,并非理论的一部分。PBE对酸碱质子理论的学习也没有辅助作用;需要先熟悉理论,然后才有可能建立PBE。
“去公式化”新体系中,物料平衡式MBE是解决各种问题的着手点,是最重要的概念之一。MBE的建立规则:1) 基于化合物的分子构成列出等式;2) 如果有化学反应,那么“反应剩余+反应消耗−其他来源=总量”;3) “反应消耗”根据化学反应计量关系列出。建立MBE的例题可以参考文献[2]。
需要指出的是,计算时不必列出所有MBE,尤其对于简单问题;如果平衡体系比较复杂、未知量较多时,那么需要列出足够的MBE。
4 新课程体系的优势
与传统课程体系相比,“去公式化”新体系具有明显优势。
新课程体系是有趣的。新体系的机械记忆负担轻,因为不再包含大量的传统公式。以pH计算为例[3],新方法包括3个步骤:1) 列出CBE;2) 将CBE整理为包含[H+]的方程;3) 求解该方程。对于第3步中的方程,目前有很多软件可以求解,我们也开发了针对化学平衡特点的求解软件和手机APP[4],下载地址在第5小节“新课程体系的资源”中介绍。记忆负担的减轻可以显著提升学习兴趣,鼓励主动思考,促进教学相长。
新课程体系是统一的。各种看起来不同的分析化学问题,在新体系中都可以按照相同思路来求解,这就是图1所示的理论框架。该框架统一了四大平衡的组分浓度计算,如上面提及的pH计算;统一了四大滴定终点误差的计算[5,6],统一了四大滴定曲线的精确绘制[7];统一了准确滴定判别的实施[8]。这种统一模式强化了化学平衡定量解析知识的系统性,进而凸显了分析化学的科学性——具有完整、自洽的理论。
新课程体系是精确的。这里指方法、思路的精确,因为计算过程中没有任何近似手段。相比之下,传统体系颇为倚重近似手段,借以导出简单公式;公式都有适用条件,借以控制结果误差。但是,对于无公式可用的复杂问题,如果仍然采用传统方式,那么失之毫厘的近似,可能导致谬以千里的结果。显然,新体系的精确求解能够解决这一问题,我们因此不必担心近似手段导致的误差。
新课程体系是强大的。新体系是关于化学平衡定量解析的一般性方法。因此,简单问题和复杂问题的解决思路完全一致,只是最终方程的复杂程度不同,而方程的求解由软件完成。使用新体系的解析策略,一方面,传统难题变得不再困难,传统解题技巧已变成更广泛背景下的特例;另一方面,学生能够举一反三,面对没见过的“新问题”仍有求解思路,不至于无公式可用而束手无策。“举一反三”体现的是大学基础课要着力培养的学生核心素养。
新课程体系是与时俱进的。新体系涉及的方程求解和图像绘制都采用当前流行的数据处理平台,如Matlab和Octave。教材附录提供程序源代码以便参考[9]。这种方式既提高计算效率,又使本科生在低年级就能接触到大数据时代的问题解决策略和技术。
新课程体系是高效的。新体系的基石是图1所示的理论框架,各种具体问题的求解只是这个框架的应用。教师讲授这个框架和相应例题即可,不必花费更多课时去介绍各类问题的传统计算公式及其推导。这样不仅能够为关键知识点分配足够课时,还可以拓展知识的深度和广度,如能斯特方程计算值的误差研究[10]。
5 新课程体系的资源
新课程体系已经具有完整的教学资源。教材《分析化学》(第2版)和教辅《分析化学题解——基于去公式化计算策略》分别于2020年和2019年出版[9,11]。完整课件可以在http://staff.ustc.edu.cn/~lshao/misc.html免费下载。
开发了教学辅助软件,包括方程求解软件、分析化学数据库软件和数理统计工具软件[3,11],软件下载页面为http://staff.ustc.edu.cn/~lshao/misc.html。这些软件的作用是辅助教学,学生仍然是学习主体,是解题思路的设计者和解决方案的提供者。
新课程体系MOOC已经在“智慧树”网站运行(https://www.zhihuishu.com/),在网页上通过关键词“去公式化分析化学”搜索到该课程,然后开始学习。MOOC课程视频发布在B站(https://www.bilibili.com),在网页上通过关键词“邵利民”即可搜索到。
6 新课程体系的考试
新课程体系与传统体系的知识内容相同,因此试题也相同。换言之,传统体系中长期积累的试题可用于新体系。有所改变的是计算题的评分标准和区分度,因为新体系采用不同的求解策略。
新体系中,计算题评分标准是解题思路的正确性和解题步骤的完整性,不要求最终计算结果。这是因为一些复杂问题的精确求解需要软件,而软件使用受到考场限制。实际科研或者工程中,几乎不存在无法使用软件处理复杂问题的情形,而脱离实际的考试没有太大价值,所以这种评分方式是合理的。当然,对于一些通过计算器就能完成的简单题,最终计算结果仍占一定分值。
传统体系中,一些计算难题涉及复杂公式的运用,因此有一定的区分度(其实是考查机械记忆力)。这些“难题”在新体系中的区分度下降,因为解题思路与“简单题”完全相同。解决方法:1) 适当降低传统计算题的分值,或者改造题目以减少纯记忆性知识的运用;2) 设计考查学生思考和推理能力的开放性试题。下面是我们设计的一道试题和评分标准,供同行教师参考和指正。
考题(10分):有研究表明,HF溶液中存在以下两种平衡:
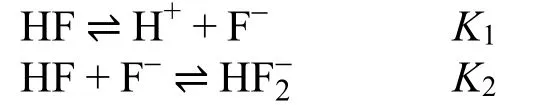
对于分析浓度为cmol·L−1的HF溶液,请给出pH计算方案。
参考答案及评分标准:
平衡体系的CBE如下:

关于氟的MBE如下:

(正确列出CBE、MBE并完成相应推导,每式得4分)
通过式(2)得到[H+]的表达式,将之代入式(1)后得到关于[F−]的方程,解此方程得到[F−],将之代入式(1)或者式(2),计算出[H+]。(写出求解方案的必要步骤,得2分)
该试题基于一篇科研论文[12],属于学生在课堂上没有接触过的“新问题”。该题不仅考查学生的基础知识——掌握CBE、MBE和平衡常数等概念,而且考查其运用基础知识解决复杂问题的能力——从初始条件出发逐步推导出包含目标量的方程。与套用公式求解的试题相比,这类试题能够更全面地反映学生的综合能力。
传统考题中有一些选择题或者填空题就是套用公式直接计算。如果条件允许,可以将这些题改造为普通计算题,这样学生就能够展示求解过程,从而避免完全基于结果的评分。
新课程体系考试的重点在于考查学生的分析推理能力和信息综合能力,不强调纯记忆性知识,在全面性、客观性和灵活性方面更具优势。与此同时,对教师在试题设计和阅卷方面提出更高要求。
7 新课程体系的实践
2017年开始,新课程体系在中国科学技术大学“分析化学I”课堂正式使用。该课程面向化学、材料、生物和地球化学专业,2学分、40学时,春季和秋季两学期开设。修课学生每学年约有300人,是相关学院的一年级或者二年级本科生。五年来的教学实践和学生反馈表明教学效果良好,以下摘录部分学生反馈。
学生一:“能够减轻很多记忆负担,同时对于复杂体系也能从容地处理。”
学生二:“从本质上理解知识后,发现同一类题不管如何变化都可得以解决。相对于传统的做法,少了许多公式的记忆,个人觉得使课程更有趣。”
学生三:“确实能让我们少记许多公式,而且对问题的本质有了更深刻的认识,也锻炼了处理问题的思维,能够很好地进行拓展和推广以解决其他的类似问题。”
学生四:“更重要的一点,这门课培养了我一种思考方式:不是时刻想着如何能够使解题过程简单,而是尽量争取精确求解。”
学生五:“从思维上来说,这种方法是极为简单的,同时又是最本质的(直接利用体系中的守恒关系和平衡常数表达式就可以推出很复杂的结果),我觉得这是我收获最大的一点,也希望这种方法能够更加推广开来,让更多的学生受益。”
物理学院选课学生:“以CBE、MBE等基本方程为出发点,应用于具体化学系统中,求得基本变量。这种分析思路和物理学方法是异曲同工的。”
8 结语
分析化学传统课程体系是计算工具欠发达年代的产物,特点是“记忆换运算”和“近似换简化”。传统体系是一种封闭模式,只能解决公式可以覆盖的问题;公式适用范围之外的问题便无能为力,勉强将公式外推,纵然得到结果,也无法判断误差有多大。
“去公式化”新课程体系是一种开放模式,从普适的基本等量关系出发求解化学平衡问题。中国科学技术大学五年的课堂实践表明,新体系不仅显著减轻了学生的机械记忆负担,而且使他们摆脱公式限制、开拓思路、深入研究化学平衡。
新课程体系不再包含大量导出公式。但是,“去公式化”不等于彻底摒弃公式。新体系仍然保留了少量方便易用的公式,如pH估算式,在精确度要求不高的场合可以快速算出pH近似值;再如林邦公式,在EDTA准确滴定判别中的效率较高。当然,这些问题通过“去公式化”方法也可以完成。
新课程体系对化学平衡能够进行精确解析。但是,“去公式化”不等于否定传统体系的价值。传统体系为了克服早期计算困难,引入近似手段以得到简单算式;为了控制误差,引入适用条件,用于解决不同类型的问题。这种“引入近似分类处理”是不利条件下的有效策略,值得学习,也应该在授课中向学生说明。
新课程体系得益于普适计算(pervasive computing),即功能强大的计算设备已经普及(包括台式机、笔记本电脑、平板电脑和智能手机)。但是,“去公式化”不等于必须依靠计算机和软件;思路是关键,硬件和软件只是实现方式。

