自由空间光通信下对称Spinal码的性能分析

张 兢,杜凡丁,曹 阳,彭小峰

(重庆理工大学电气与电子工程学院 重点实验室,重庆 400054)

1 引 言

在长距离的自由空间光(FSO)通信如卫星与地面间的通信中,信号强度会受到湍流、散射、吸收等众多因素的影响[1],其中大气湍流对光的传输影响最大。大气湍流的存在会干扰光束在长距离FSO通信中的传输[2],降低通信系统的性能[3],严重影响FSO通信质量[4-5]。因此,许多信道编码的方案被应用于长距离FSO通信系统中以保证其稳定性和可靠性,如使用低密度奇偶校验码(LDPC)[6]、Turbo码[7]和近几年新兴的极化码(Polar Code)[8-9]。但这些编码方案在面对突发差错如信道质量突然下降时误码率会增大；同时它们的编码速率相对较高,在低码率下的编码增益较低。因此无速率码LT码[10]和Spinal码在FSO通信中受到了广泛关注。

Spinal码最早由Perry在文献[11]中提出,Spinal编码具有编码结构简单、在二进制对称信道(BSC)和加性高斯白噪声(AWGN)信道上可以证明接近信道容量的特性[11-13]。Perry在文献[13]中证明了Spinal码具有比LDPC等固定速率码更高的吞吐量。文献[14]中提出的混沌映射方法有效降低了Spinal码的计算复杂度。与传统的编码不同Spinal码的核心为非线性散列函数,这使得Spinal码在噪声和干扰下具有良好的鲁棒性[14]。作为一种新兴的无速率码Spinal码的传输速率会随信道质量的好坏自适应变化,当FSO通信由于大气湍流等因素出现突发错误时,Spinal码可以适当降低传输速率以保证译码的正确性,其无需反馈即可自适应地传输,适用于反馈重传时延极长且存在大气湍流的星地通信。这些优良特性显现出Spinal码应用于FSO通信的巨大潜力。但在FSO通信中Spinal仍面临着诸多问题。

Spinal码受其潜在的不等差错保护性的影响,有着差错控制性能不佳的问题。其误码率主要受到最后一段编码的性能影响。此外Spinal码译码的复杂度较高,编译码速度有待提高。针对以上问题,本文提出一种FSO系统中的对称Spinal编码。对称Spinal码在原始Spinal码的编码基础上增加一次反向编码,对容易发生错误的编码位进行保护以提高其在FSO差错控制性能。并使用相应的迭代译码方法降低译码复杂度。

2 星地激光信道模型

在卫星与地面通信的信道中,激光的传输会受到湍流影响。大气湍流[15]会使接收光功率发生衰减,由对数正态分布得到大气湍流弱扰动下接收光功率的概率密度函数(PDF)。当接收光功率为I且其平均值为“I”时,I的PDF如下式:

(1)

式中,σ2是I的分布情况,也是大气湍流指数,被称为闪烁指数(SI)。当SI较高时,接收到的光功率会产生很大变化。在大气湍流引起的强干扰的情况下,I的PDF由双伽马(Gamma-Gamma)分布得到,如下所示:

I>0

(2)

式中,Γ()是伽马函数;Kα(β)是第二类修正贝塞尔函数,其中α和β分别表示大湍流尺度和小湍流尺度,它们与大气条件有关,由公式(3)，(4)给出:

(3)

(4)

σ2是根据α和β得到的:

(5)

3 大气湍流信道下的对称Spinal码

图1 Spinal码编码结构Fig.1 Spinal code encoding structure

si=h(si-1,mi)

(6)

其中,si为哈希函数的种子值,与mi一同作为哈希函数的输入。s0作为最初的种子是为发送端与接收端所共同知晓的；s0与m1作为哈希函数的输入得到的s1,会作为新的种子与m2一同输入哈希函数。同时s1作为一个Spinal值经过随机序列发生器(RNG)和映射(Mapper)生成无限长的发送序列x1,从中截取c位数据得到x1,i进行m1的一次传输。其余信息段也是如此。x1,1,x2,1,…,xk,1组成了信息M的一个完整传输过程,该过程称为一个pass。如果接收端在收到第一个pass后就成功译码,则其实现较高传输速率；当受到湍流等因素影响导致信道质量突然变差,接收端在收到多个pass后才成功译码,则导致传输速率有所下降,以此保证译码正确率,这就是Spinal码的无速率特性。

一般的Spinal码在译码发生错误时,错误总是出现在最后几位的Spinal码上,这种现象意味着Spinal编码具有潜在的不等差错保护(UEP)的特性。然而,在实际的应用中,Spinal编码的结构并不灵活,不能满足UEP的不同层次的要求。

(7)

(8)

因为其连续编码的特点,只有x1,…,xk携带m1,…,mk的信息,所以根据上式很容易分析出在Spinal编码中前一段信息的性能总是优于后一段信息,这证明了Spinal码的UEP性质。又因为最后一段信息mk与前面的x1,…,xk-1无关,所以只有xk与其有关,因此可以将公式(7)近似为:

Pe≥δD

(9)

通过将Spinal码的传输pass数设置为L,可以将这样的固定速率的Spinal码表示为Ccapacity(n,k,L),而上式中的δD可以视作一个短Spinal码Ccapacity(k,k,L)的误码率。所以一般我们认为Spinal码的差错控制性能受最后一段的性能影响。因此本文使用了一种对称的Spinal编码来解决以上问题。

对称Spinal编码方式在Spinal编码的基础上,增加了一次反向的编码过程,以达到改善Spinal码差错控制性能、提高传输速率和抗干扰的目的。

如图2所示,对称Spinal编码结构由正向编码与反向编码两个部分组成,正向与反向编码都是一次Spinal编码。前向编码的哈希状态及其哈希函数表示为:

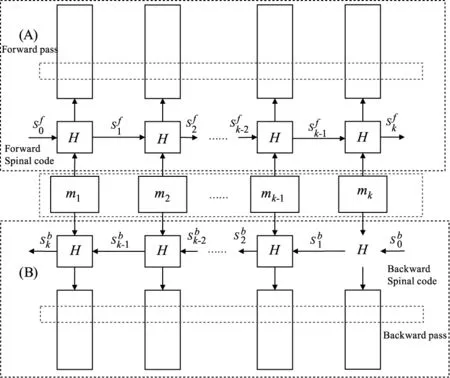
图2 对称Spinal码的编码结构Fig.2 Symmetric Spinal code encoding structure

而后向编码的哈希状态及其哈希函数表示为:

Algorithm 11:Create and initialize the forward tree M with Mi=(,1,…,2k-1);2:Create and initialize the max node number B and the iteration number lmax;3:for l =1 to lmax do4:Search the forward tree M,and save the nodes which their channel inputs and the received symbols matched;5:Update M with the result M=(M1,…,Mk),n is the number of survival nodes;6:Create the backward tree M'=(Mk,…,M1) with the Updated forward tree M;7:Search the backward tree M',and save the nodes which their channel inputs and the received symbols matched;8:Update M' with the result M'=(Mk,…,M1);9:Next forward tree M will be created by M';10:if for each i,the Mi has a unique solution 11:break12:end if13:end for14:Output the survival nodes in M

首先定义一个表M=(M1,…,Mk)存储所有的信息可能值,Mi最多可以存储2k个值；在译码开始时,先对Mi进行初始化,其中每一个指针表示消息Mi的候选值索引。译码器使用表M在前向编码树中搜索输入输出相匹配的可能值。经过一次完整的搜索,保留这些符合条件的可能值,将不符合条件的值从表中删除。这样就完成一次对表M的更新。基于这个新的表M生成一个表M′=(Mk,…,M1)。译码器再使用M′对后向编码树进行搜索,将后向编码树中输入与输出相匹配的可能值保留在M′中,删除不匹配的可能值,然后对M′中的可能值进行更新。一次迭代完成。在下一次迭代开始时,基于表M′中的可能值对表M进行一次更新。在经过多次迭代后对于M=(M1,…,Mk)中的每一个Mi只有一个可能的值时,代表成功译码。

除此之外还要加入一个远小于2n的参数B,来限制每一次前向搜索和后向搜索的最大节点数。当已搜索到的节点数大于B,则终止译码。

4 仿真与分析

针对本文提出的方案使用Matlab进行仿真。模拟了大气湍流信道,调制方式使用二进制相移键控(BPSK)。仿真对比了对称Spinal码与原始的Spinal码在不同信噪比(SNR)下的传输速率,并同无速率LT码[17]作对比。对称Spinal码与Spinal码的参数取值均为:k=4,c=10,哈希函数选取为Jenkins one-at-a-time。传输速率如图3所示。

图3 LT码,Spinal和对称Spinal码传输速率性能Fig.3 Rate performance of LT code,Spinal code and Symmetric Spinal code

由图3可明显获知,同为无速率码Spinal具有比LT码更好的传输速率。而对称Spinal码在Spinal码的基础上传输速率又有所提升。具体数据如表1所示。

表1 三种无速率码在不同SNR下的传输速率Tab.1 Different rateless codes rate performance in different SNR

由表1可知,随着SNR的提高,Spinal码与LT码的传输速率性能差距逐渐增大,而对称Spinal码与Spinal码的传输速率之差保持在0.23左右。由此可见对称Spinal码提高了传输速率,这是因为当Spinal码发生错误时,出现错误的位置一般都位于最后几位,这会导致Spinal正确译码需要接受更多的pass数,因此传输速率会受到影响；而对称Spinal码由于增加了反向编码的过程,对易出错的数据位进行了保护,减少了正确译码所需要的pass数,因此传输速率得到了提升。

本文对不同湍流强度下的对称Spinal码和Spinal码的误码率进行了仿真,各个码字BER性能如图4所示。从图4可以看出,当σ2=0.3湍流较弱时,SNR=4,Spinal码的误码率为1×10-3,而对称Spinal码的误码率为0.012,Spinal码的误码率优于对称Spinal码；SNR=9时,对称Spinal码误码率开始优于Spinal码；SNR=15时,Spinal码误码率为1.5×10-4,而对称Spinal码误码率为2.7×10-5。当湍流较强σ2=0.5时,SNR=4,Spinal误码率为2×10-3,对称Spinal码的误码率为0.03；SNR=10.5时,对称Spinal码的误码率开始优于Spinal码；SNR=15时,Spinal码误码率为2.2×10-4,而对称Spinal码误码率为 1×10-4。由此可以看出无论大气湍流的σ2=0.5还是0.3,Spinal码的误码率在SNR提升到一定程度后趋于平稳,而对称Spinal码的误码率在SNR不断提升的情况下随之降低。因此我们很容易得出,在面对FSO通信中的大气湍流时,只要提供较高的信噪比,对称Spinal码的编码方案可以带来更优秀的误码率性能。这也是由于对称Spinal码增加了一个反向编码的过程,提高了其抗干扰的性能。

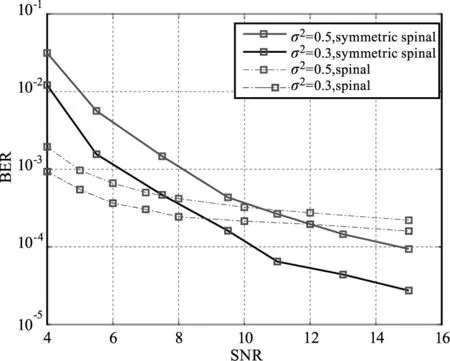
图4 Spinal码和对称Spinal码在不同湍流强度下的误码率Fig.4 BER performance of Spinal code and symmetric Spinalcode under different turbulence intensity

本文还对RS码、Spinal码、极化码与对称Spinal码的误码率进行仿真对比。除Spinal码和对称Spinal码外,还使用了(8,15)的RS码,以及连续删除(SC)译码的polar码,polar码长为256,码率为0.5。误码率如图5。

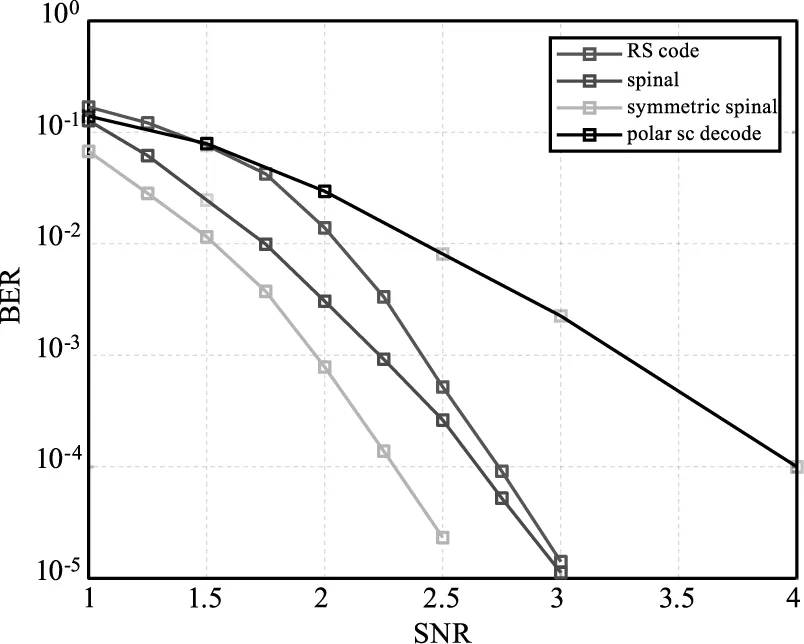
图5 RS码、Spinal码、Polar码和对称Spinal码的误码率对比Fig.5 BER performance of RS code,Polar code,Spinal codeand symmetric Spinal code

由图5易知,对称Spinal码的误码率性能最优。BER=1×10-2时,对称Spinal码相比Spinal码,RS码和极化码分别产生了0.25 dB,0.6 dB和1 dB的增益；BER=1×10-3时,增益分别为0.3 dB,0.45 dB和1.3 dB；BER=1×10-4,增益分别为0.4 dB,0.5 dB和1.75 dB。由于Polar码码长较短,其误码率性能在四种编码中最差,当SNR小于2时它的误码性能与RS码相近,而当SNR=3时,RS的误码率降低到了1.4×10-5,Polar码的误码率则为2.2×10-3；Spinal码的误码率在SNR小于2.5时明显优于RS码,而当SNR=3时,两种编码的误码率仅相差3×10-6。对称Spinal码的误码率明显优于其他三种编码:当SNR=1时误码率为0.067,比Spinal码的误码率低0.006；当SNR=2.5时误码率为2.3×10-5,比Spinal码的误码率低2.4×10-4。因此,对称Spinal的差错控制性能明显优于RS码,Polar码与原始的Spinal码。

5 结 论

本文提出的FSO通信中的对称Spinal码方案,在原始Spinal编码的基础上增加了一次反向编码改善其差错控制性能,并通过相应的迭代译码算法降低译码复杂度。仿真结果表明,SNR在-5～10的范围内时,对称Spinal码的传输速率始终优于原始Spinal码以及LT码；在SNR较高的情况下,对称Spinal码在面对FSO通信信道中的大气湍流时具有更好的抗干扰能力；对称Spinal码的差错控制性能在明显优于原始Spinal、RS码以及Polar码,在不同BER下相比于原始Spinal码均产生了不同程度的增益。