邻近基坑降水引起高速磁浮墩柱沉降的初步估算
唐宛玉 叶 丰 王国强 吕 卿
1. 中国电建中南勘测设计研究院 湖南 长沙 410007;2. 同济大学磁浮交通工程技术研究中心 上海 201804;3. 上海磁浮交通发展有限公司 上海 201204
上海高速磁浮示范线(以下简称上海线)用于连接上海浦东国际机场和龙阳路地铁站,是目前世界上运营时速最快(最高430 km/h)的陆地交通系统。它具有精度要求高、速度快、技术含量高、影响力大等特点,是上海城市轨道交通系统的重要组成部分。线路轨道系统的稳定是上海线在17年运营过程中准点、高效和安全的重要保证。《上海市轨道交通安全保护区暂行管理规定》中规定了城市轨道交通保护区的范围。参照该规定,磁浮运营单位将磁浮外边线拓展30 m之内的区域设为高速磁浮线安全保护区。在此范围内的工程项目建设需要得到有关部门审批,并从设计、评估、施工和监测等各环节进行综合监护。在此范围之外的工程一般不作硬性规定。但在特定情况下(如基坑降水),保护区外的施工也会对磁浮线路产生显著影响,此时需要结合项目情况进行预判,看是否需要启动类似于保护区内工程的综合技术监护。因此,对这类工程项目,无论其是否处于安全保护区内,在前期阶段预估其对磁浮线路轨道结构的影响具有重要的参考意义。
高速磁浮列车对轨道结构变形相较于其他轨道交通系统更为敏感。根据《上海磁浮交通发展有限公司磁浮安全保护区管理办法》,结合磁浮系统的有关技术要求,外部工程施工引起的磁浮轨道结构基础附加竖向变形不得超过2 mm。随着城市发展,磁浮线附近经常出现需要进行降水的深基坑工程。基坑降水是一个复杂的流固耦合过程,目前基坑降水导致桥梁桩基沉降的计算方法还没有形成一套完整的体系[1],针对高速磁浮系统的类似研究尚为空白。
黄发安[2]通过对各种桩基沉降计算方法进行对比,得出等代墩基法等方法可用于计算桩基沉降,但并未考虑土层中水位变化引起的桩基变形应如何计算。宋建学等[3]和宋丹举等[4]通过研究得出基坑降水形成的降水漏斗曲面函数与抽水影响半径呈对应关系,提出了简化的降水沉降分层总和法计算公式,并结合郑州地区某工程实例,认为该区域分层总和法沉降修正系数可取0.24~0.33。刘御刚[5]通过对某高铁墩桩基础进行分析,得出在水位变化时,桩周沉降导致桩侧摩阻力变化,引起桩基沉降的结论。上述研究均表明,地下水位变化会引起桩基工作性状的改变,从而产生沉降变形;分层总和法及其变式应用于桩基沉降或降水引起的地表沉降计算中是可行的。但是目前研究多集中于对一般建筑物或高铁桩基沉降计算方法的探讨,修正系数也随着地区的不同而变化。上海线轨道精度要求高,桩基较深,周边区域属于典型的天然软土地区,土质条件不利。外界基坑降水引起的磁浮处水位变化预测以及由此引起的沉降估算,可以借鉴这些研究成果进一步探讨。
1 基坑降水引起磁浮结构处降深的分析方法
基坑工程在施工时,多为边开挖边降水。确定基坑降水引起的周围环境水位降深变化的方式一般有3种:现场监测,在基坑开挖周边设置观测井,直接对周边地区水位变化进行监测,得到实时水位降深变化值;数值软件模拟,目前有多款可以用于渗流计算的数值软件,如MODFLOW等,可以通过模拟渗流过程得到预测水位降深值;利用经典经验公式直接计算。其中,现场监测获取的数据,准确性、真实性高,但是需要在现场设置多个观测井,工程造价高,且费时费力;软件模拟计算是根据相关勘察报告和水文地质资料建立相应的三维模型,可以考虑含水层的非均质性以及止水帷幕等结构产生的影响,但仍需要引入许多假定和简化,对成本和技术要求较高;经验公式法针对的是假定的理想状态,计算最为简便快捷,适用于工程前期在资料和试验不足的情况下快速定性估算。
1857年,法国水力学学者裘布依将当时的渗流相关定律应用到土体含水层中,得出了著名的裘布依微分方程。裘布依公式给出了抽水井周边地区含水层中水位降深变化与抽水井距离之间的关系,简单易行,是目前较为常用的计算方法。根据裘布依稳定承压井流计算理论,基坑远离边界的条件下,在等效的抽水井(即基坑)外侧距离为r处的水位降深[6],如式(1)所示。
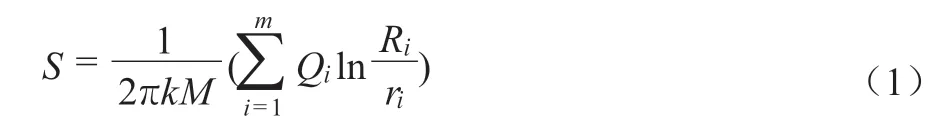
式中:S ——降水场区内任意点的水位降深,m;
k ——渗流系数,m/d;
M ——承压含水层厚度,m;
Qi——第i个降水井的出水量,m3/d;
Ri——第i个降水井的影响半径,m;
ri——计算降深点到各个井点中心的距离,m;
n——降水井的个数。
邻近基坑降水引起的磁浮结构处降深可以参考上述裘布依经验公式进行估算。
2 水位降深变化引起的土体沉降计算
土体由固、液、气三相组成,抽降水使土层孔隙水排出,气相体积减小,土体骨架发生错动,从而造成土体变形。土体总应力由有效应力和孔隙水压力组成,基坑降水使基坑周围地区地下水位发生变化,孔隙水流失导致土体中孔压降低,有效应力增加,土体发生压缩沉降[7]。目前计算土体沉降多采用分层总和法,该法作为规范中推荐使用的方法,以半空间各向同性弹性理论为基础,由固结试验中所测得的参数来表征土体压缩特性。《城市软土基坑及隧道工程对邻近建筑影响评价与控制技术指南》采用式(2)计算降水引起的地面沉降量[8]。

式中:S——降水引起的建筑物基础或地面的固结沉降量,m;
ψw——沉降计算经验系数;
Δ σ′zi——降水引起的地面下第i土层中点处的有效应力增量,kPa;
Δhi——第i层土的厚度,m;
Esi——第i层土的压缩模量,MPa;
n ——计算的地层层数。
基坑外土中各点降水引起的有效应力增量可根据计算的地下水位降深,按照下式计算:
1)计算点位于初始地下水位以上时,Δ σ′zi=0。
2)计算点位于降水水位与初始地下水位之间时,Δ σ′zi=γwa0。
3)计算点位于降水水位以下时,Δ σ′zi=γwsi。其中,γw为水的重度,si为计算点对应的地下水位降深,a0为计算点至初始地下水位的垂直距离。
在工程前期阶段估算时,不妨假定土体总沉降与磁浮墩柱沉降相当,用于定性判断。在后续定量分析中,应考虑土体与桩基之间相互作用对沉降的影响。
3 工程实例
因项目建设需要,上海线附近某深基坑工程需要进行基坑降水作业。该基坑工程距离上海线较远,位于安全保护区外,按现行管理规定无需强制履行保护区审批程序。考虑到降水作业影响范围较大,应当在项目前期进行初步估算和预判,以便快速判断其是否需要实施专题评价并组织综合技术监护。
3.1 工程概况
3.1.1 工程简介
某基坑位于上海市浦东新区,长76 m,宽55 m,开挖深度为42.1~45.5 m。最近点距离上海线90.7 m。该基坑底部位于中层粉质黏土中,围护结构为地下连续墙,厚1.2 m,止水帷幕深89.8 m。上海线轨道为高架结构,采用桩基础。根据相关资料,该工程范围内上海线桩基采用φ600 mm钻孔灌注桩,长度为71~75 m,桩端持力层位于青灰色粉细砂层(⑨层)中。基坑与上海线墩柱相对位置关系如图1所示。

图1 基坑与上海线墩柱相对位置关系
3.1.2 工程地质条件及水文地质条件
上海地区属于典型的天然软土地基,表现为外荷作用下压缩变形量大、抗剪强度低、透水性差、流变特征明显等不良特性[9]。该基坑处地质条件与邻近的上海线墩柱相近,二者之间地质情况视为水平均质,工程范围内土体多由粉质黏土、粉性土及砂土组成,相关参数如表1所示。
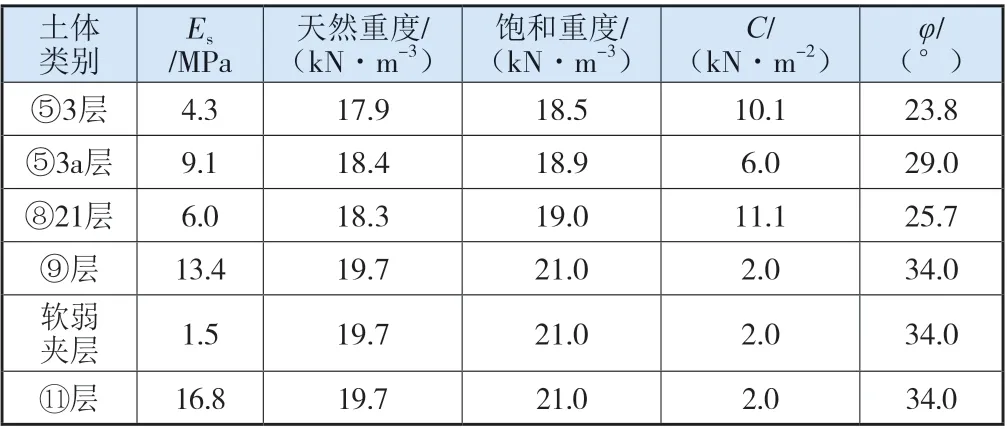
表1 主要土层相关计算参数
浅部地层水为第四系孔隙水,以潜水为主。深部土层主要影响含水层有3层,第⑦层第1承压含水层、第⑨层第2承压含水层和第 层第3承压含水层,⑦、⑨与 层含水层间具有水力联系,形成含水层组。
3.2 水位降深确定
根据工程设计方提供的基坑降水参数,可以确定式(1)中的相关参数,如表2所示。

表2 各含水层基坑降水参数
由表2可知,止水帷幕深入⑨层,由于公式计算无法考虑阻水结构带来的影响,仅对⑨层、 层进行水位降深计算分析。按计划,该工程拟在距离基坑5.0、13.0、58.3、81.3、90.7(上海线距离最近处)、117.7、138.9 m处布置观测井,监测水位降深。为此,应用式(1)计算上述各点降深,如表3所示。

表3 经验公式计算⑨层及 层各监测点水位降深 单位:m
3.2.1 与数值模拟结果对比
由于该基坑工程降水规模很大,故工程设计方在前期应用数值软件模拟分析了基坑外一定范围内的降深。各监测点模拟结果如表4所示。

表4 数值模拟⑨层及 层各监测点水位降深 单位:m
经验公式和数值模拟的对比结果如图2、图3所示。由图可见,2种计算水位降深随着距离的变化趋势相同,各监测点与基坑位置距离增大时,水位降深随之减小。第⑨层水位降深计算值与模拟值差异较大,第 层拟合结果相对较好。这可能是因为止水帷幕深入⑨层,起到了一定的阻流效果,而经验公式无法考虑阻水结构造成的影响。

图2 第⑨层水位降深计算值对比

图3 第 层水位降深计算值对比
3.2.2 以基坑外5 m处为基准点计算
由于经验公式未考虑阻水结构的影响,故以基坑外5 m处为基准点,将软件模拟值设为初始计算值,应用式
(1)计算各监测点处层预估降深,结果如图4所示。各点位处软件计算值与公式估算值误差在5%之内,2种计算结果吻合较好,进一步说明软件模拟值与经验公式估算值之间的差异主要是由止水帷幕作用造成的。

图4 以基坑外5 m处水位降深为基准点的公式对比计算
以上分析表明,在项目初期阶段,可以用经验公式来定性估算磁浮结构处的水位降深。
3.3 土体沉降计算
运用式(1)计算得到上海线墩柱处⑨层及 层水位降深分别为6.42、2.21 m,代入式(2)可计算水位变化引起的土体沉降。根据JGJ 94—2008《建筑桩基技术规范》,桩中心距小于6倍桩径的桩基,最终沉降量可采用等效作用分层总和法,作用面选为桩端平面。磁浮桩长72 m左右,桩端平面以下为⑨层及 层,计算沉降值为25.3 mm。
目前,上海市地方标准对地下水引起的地面沉降修正系数尚无明确规定,因此,工程中参考了北京市地方标准DB11/1115—2014《城市建设工程地下水控制技术规范》中关于降水引起的沉降经验修正系数,一般第四纪沉积地层可按照表5取值。表中北京地区粉细砂层修正系数取值0.4~0.6,⑨层及 层均为粉细砂层,且土层较厚,可以取小值。但是考虑到上海地区与北京地区土质相比较软,沉降系数取值适当放大,⑨层取0.6, 层取0.5。按照沉降经验修正系数计算后,最终根据经验公式预测水位计算沉降值为14.7 mm。

表5 沉降经验修正系数
由上节可知,经验公式估算的水位降深值,未考虑止水帷幕的阻水作用,因此相应沉降计算结果偏大。若以前节中基坑外5 m处为基准点,则磁浮处降深估算介于2.0~2.5 m之间,若据此对沉降值进行适当折减,仍可达4 mm左右,超出了墩柱变形限值,说明该基坑降水虽位于上海线保护区外较远处,但对上海线墩柱沉降的影响仍相当显著,应当进行专题研究,并参照安全保护区内工程施工履行相应的审批和监护程序。
由于前期预估的沉降值偏大,因此该工程需要考虑优化降水施工过程,并适当考虑地下水回灌来减少上海线处墩柱沉降。同时,在该工程设计、评估、施工和监测等各环节应当进行综合技术监护。施工过程中,必须实时监测土层中水位变化,以确保上海线的安全运营。
4 结语
1)对于上海线周边深基坑降水工程,可以用裘布依公式和分层总和法进行初步估算,能方便快捷地得到磁浮墩柱沉降预估值,可判断是否需要进行专题分析和履行审批程序。
2)工程实例的估算表明,即使距离很远,基坑降水对磁浮墩柱沉降的影响仍不容忽视。
3)从技术管理角度而言,外部施工对磁浮结构的影响不应局限于30 m范围,应对相关管理规定进行适当完善。
综上所述,经验公式在定量计算上有其局限性,但因其方便快捷,在外部工程项目前期阶段可用于预估其对磁浮墩柱沉降的影响,协助各方判断是否要履行相应审批程序。在专题分析阶段,则应通过实测或软件仿真模拟等更为精确的计算方法进一步修正上述经验公式预估的结果。

[1] 高胜君,罗书学,黄锐,等.软黏土条件下地下水位变化对桥梁桩基的影响分析[J].路基工程,2017(2):102-105.
[2] 黄发安.桩基沉降分析与计算[D].成都:西南交通大学,2006.
[3] 宋建学,周乃军,邓攀.基坑降水引起的环境变形研究[J].建筑科学,2006,22(3):26-30.
[4] 宋丹举,宋建学,翟永亮.基坑降水引起的地面沉降简化计算模式及地区修正系数的研究[J].建筑科学,2012,28(1):78-80.
[5] 刘御刚.抽降水对高速铁路桥梁桩基的影响分析[D].长沙:中南大学,2014.
[6] 刘国彬,王卫东.基坑工程手册[M].2版.北京:中国建筑工业出版社,2009.
[7] TERZAGHI K T.Theoretical soil mechanics[M].New York:Wiley and Sons,1943.
[8] 中国土木工程学会.城市软土基坑与隧道工程对邻近建(构)筑物影响评价与控制技术指南[M].北京:中国建筑工业出版社,2017.
[9] 周学明,袁良英,蔡坚强,等.上海地区软土分布特征及软土地基变形实例浅析[J].上海地质,2005(4):6-9.

