风光发电与电动汽车充放电协同优化调度

杨秀茹，郭兴众，王 昊

（安徽工程大学高端装备先进感知与智能控制教育部重点实验室，安徽 芜湖 241000）

引 言

随着化石能源日益枯竭和环境污染问题不断加剧，风光等清洁能源得到了大力的发展。电动汽车作为一种新型清洁能源交通工具，对节能减排将有巨大的贡献［1］。电动汽车对电网的影响与电动汽车接入电网充电的数量密切相关，若接入电网的数量较少时，充电行为不会对电网造成太大的负面影响；当电动汽车接入电网的数量较多时，会引起配电网的负荷波动问题。随着电动汽车日益成为常见交通工具，大量电动汽车无序充电将会对经济和安全产生严重威胁［2］。

基于电动汽车与电网（V2G，Vehicle-to-grid）互动模式，在合理的充放电调度下对电动汽车与风光发电进行协调优化，可以有效降低风光发电以及大量电动汽车接入电网时引起的波动［3-4］。目前对电动汽车充放电和风光发电协同并网已有学者进行了研究［5-8］。文献［9-10］研究了V2G模式下电动汽车有序入网的经济调度问题，结果表明V2G技术有利于降低电网负荷波动以及降低用户充放电费用。文献［11］以光伏发电入网的净负荷最低为目标函数，同时定量分析电动汽车响应调度后电网的负荷特性，提出不同光的渗透率下均能有效平抑可再生能源波动。文献［12］研究了环境和存储系统损耗，采用改进的粒子群算法对运行成本和环境治理成本模型进行了优化调度。文献［13］提出了基于电价和碳配额双重激励协同博弈的含电动汽车微电网的优化调度策略。文献［14］基于工业、商业和居民3 个区域的情景，考虑了中间商利益问题，利用遗传算法对多目标函数进行优化调度。文献［15］建立分时电价的电动汽车双层调度模型，综合考虑了电网和用户侧的收益，但电网负荷，用户满意度等存在混沌性。文献［16］主要是利用V2G技术，建立了目标函数是电网波动最小的调度模型，但局限是没有考虑用户充电的成本。

基于V2G模式，提出一种电动汽车与风光发电系统的多目标调度模型，该模型以降低电网负荷波动以及电动汽车充放电费用为目标函数，通过采用MOPSO 算法对该模型进行分析，并寻求帕累托（Pareto）最优解（即两个目标函数最优的解集）。

1 电动汽车行为特性

1.1 V2G技术

V2G 描述的是电动汽车与电网的互动［17］。当电动汽车需要充电时，通过风光发电机组给电网供电得到电能；当电动汽车闲置时，车载电池组的电流流向电网。V2G 技术有利于平抑电网负荷波动以及减少电动汽车用户充电成本。其工作原理如图1所示。

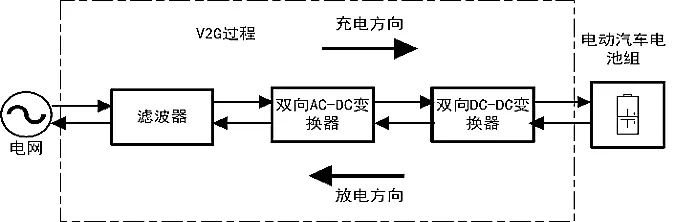
图1 V2G工作原理

1.2 电动汽车行驶行为特性

由于用户出行链几乎是不变的，电动汽车的行驶行为与传统私家车相同。根据对居民行驶规律调查统计，电动汽车每个时刻的停驶概率βp(t)如图2所示。

图2 电动汽车停驶概率

电动汽车入网的数量Np(t)：

其中，Nev为电动汽车数量。

显然，电动汽车一天90% 的时间处于停驶状态，处于停驶状态的电动汽车数量是入网电动汽车数量的最大值，电网可以对处于停驶状态的电动汽车进行优化。

电动汽车充电负荷行为不仅与电动汽车入网的数量有关，还与日行驶距离有关。将美国交通局得到的传统汽车出行数据拟合（图3），即可得出电动汽车日行驶里程规律，其服从s~log( μs,σ2s)分布，其概率密度函数为［18］：

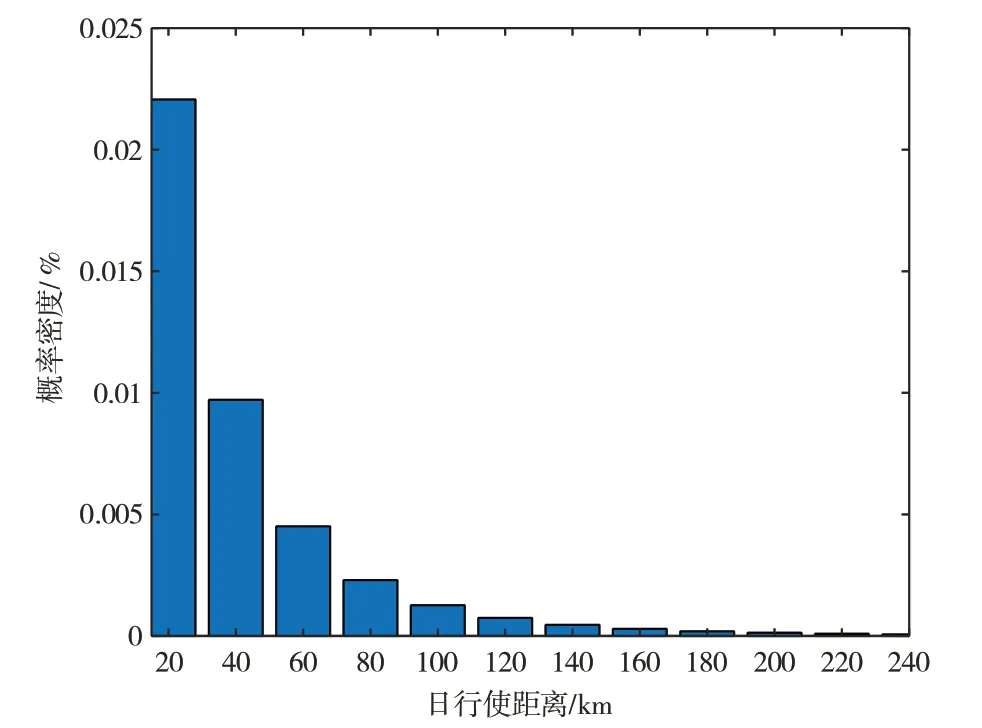
图3 日行驶距离

其中：μs= 3.2；σs= 0.88。

根据式（2）可得电动汽车日行驶里程。

电动汽车入网、离网时刻近似服从对数正态分布，如图4所示。对于出行时刻，服从正态分布，为：

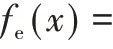
由式（3）可得出行时刻，即电动汽车离网时刻。由式（4）可得返程时刻，即电动汽车入网时刻，根据图4 可以得出电动汽车充电时刻。

图4 离网与入网时刻概率

2 多目标调度模型

2.1 目标函数

基于分时电价理论建立平抑电网波动和降低用户充电费用的多目标协同调度模型。分时电价是将一天24 h 按照负荷曲线的高峰低谷划为峰、平、谷3 种时段，对应着峰、平、谷3 种电价［19］。当处于电网负荷低谷期，可用于电动汽车充电；当处于负荷高峰期，可利用电动汽车车载电池放电。因此多目标调度模型研究主要从电网和用户侧考虑，提出了风光发电及电动汽车优化调度模型，表示如下：

（1）等效日负荷均方差最小

平抑效果可由日负荷均方差表示，日负荷均方差越小表示负荷波动越平稳，反之亦然。日负荷方差F1为：

其中：Pl(t) 为区域电网t 时段总需求负荷值；Pw(t) 为风力发电功率；Pg(t) 为光伏发电功率；Pev(t) 为充放电功率，充电取“+”；放电取“-”；Pavg为24 h 内电力系统各时段负荷的平均值。

（2）构建电动汽车充放电最小成本

基于V2G技术与分时电价制度，在峰期给电网提供电能，在谷期从电网得到电量补给，进而获得收益。因此构建电动汽车充放电成本F2为：

其中：Pc(t) 为充电负荷；Pd(t) 为放电功率；rc为充电电价；rd为放电电价；rb为电动汽车每单位容量的电池价格；Δt为计算时间长度。k为电池可充电使用次数；Cb为电池额定容量。

研究所用电动汽车电池以特斯拉为例，动力电池价格为2240 元/(kW ⋅h)；充放电次数约为1000 次；则rb=0.141元/(kW ⋅h)。

2.2 约束条件

（1）充放电时的功率约束

其中：Pcvmax为电动汽车充电产生负荷的最大值；Pdvmax为电动汽车放电产生的功率的最大值。

（2）电池剩余电量的约束

其中：E(t + 1)为时段(t + 1)电动汽车剩余电量；α为充放电系数；Ekm为1 km的耗电量；S为日行驶里程。

其中：Emin为电池存储电量的下限；Et为t 时段电池所剩电量；Emax为电池存储电量的上限。

其中：Eev为电动汽车电池容量；ε、γ 分别为最少、最多保有电量。

（3）可用时间设为24 h。

2.3 多目标优化模型

多目标优化模型为：

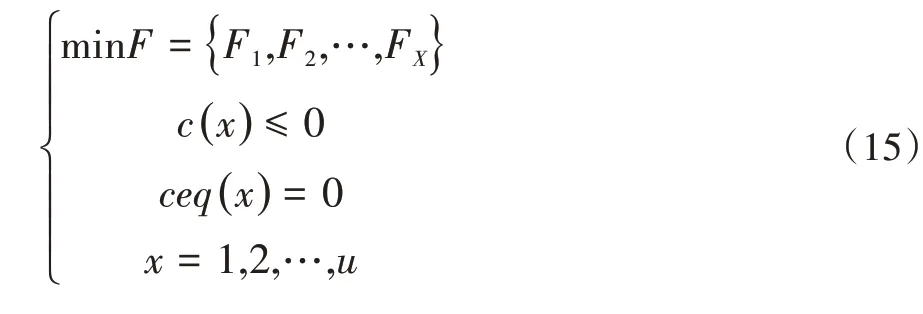
其中：x 为决策变量；c( x )表示不等式约束；ceq( x )为等式约束。FX表示粒子当前的目标函数值。

2.4 调度模型求解

电动汽车调度问题其本质是多目标优化问题。Pareto 最优解（当某个目标最优时需要通过降低其他目标函数最优为前提的解）可以有效解决目标函数会互相影响的问题［20］。多目标调度模型实际上就是一个多目标、多约束的混合优化模型，由于标准粒子群算法易陷入局部最优，所以采用基于Pareto 最优解集的多目标粒子群算法进行求解。

2.4.1 多目标粒子群算法

粒子群算法是由鸟觅食行为而来，在计算速度、收敛速度等方面具有优势。多目标粒子群算法对增加其局部搜索有效果［21］。

根据如下公式更新粒子速度和位置：

其中：i ∈[ 1,N ]；d ∈[ 1,D ]；k 为当前迭代次数，迭代次数必然大于0；c1、c2为学习因子，且c1、c2∈[ 0,2 ]，一般取2；r1、r2取( 0,1 )之间的随机数；pid为个体最优值；pgd为为群体最优值；vmax是常数，可以自行设定。

2.4.2 MOPSO求解过程

惯性权重ω 是影响粒子群算法收敛的重要因素，对于ω 不变的粒子群算法虽然具有较快的收敛速度，但由于电动汽车用户之间没有紧密联系，随机性大，易于陷入局部最优［22］。针对此问题采用了变化的ω。ω 变化如下：

其中：ωstart为初始权重；ωend为最后的权重；j为目前迭代次数；tmax为最大的迭代次数。MOPSO流程图如图5所示：

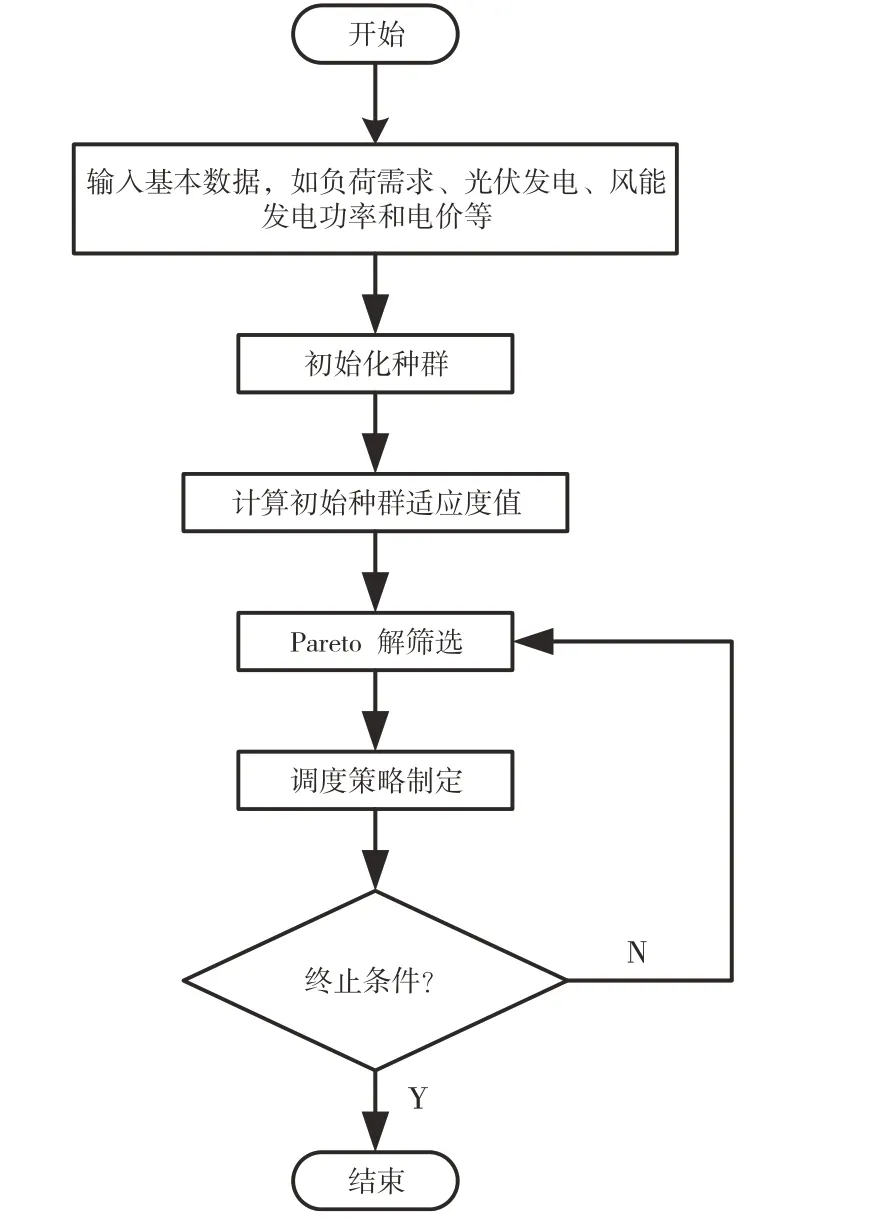
图5 多目标粒子群算法流程

3 算例分析

3.1 仿真参数设置

设定每辆电动汽车的电池容量均为22 kW ⋅h，假设电动汽车初始时刻电池均含有50% 的电量，可调度电动汽车为40000 辆，充放电功率为3.6 kW，充放电过程中的功率恒定，行驶里程为20 km，平均行驶耗电量0.14 kW⋅h⋅km-1；取ε = 0.2，γ = 0.9。粒子数为100，迭代次数为200。

假设某地区24 h 内的用电负荷以及风光发电输出功率曲线如图6所示，分时段充放电电价见表1。

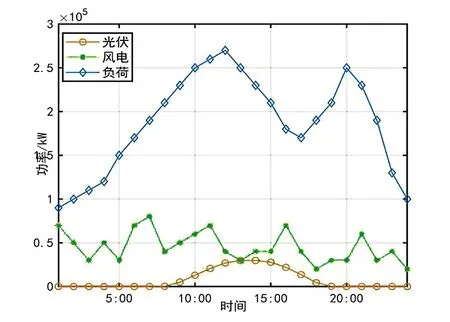
图6 某地区风光发电与负荷情况

表1 分时段充放电电价

3.2 仿真结果分析

采用MOPSO 对模型进行优化仿真。电网与用户相互博弈产生的Pareto 解集如图7 所示，其横坐标表示的是日负荷均方差，纵坐标表示的是电动汽车用户充放电成本。从图中可以看出，需要先在保证日负荷均方差最小的情况下，再考虑用户充放电成本。由于先考虑电网侧，所以用户充放电成本次要考虑。通过实验仿真结果可以看到Pareto 解集，经比较，目标函数1 数值为471.4，目标函数2数值为40.49万元。

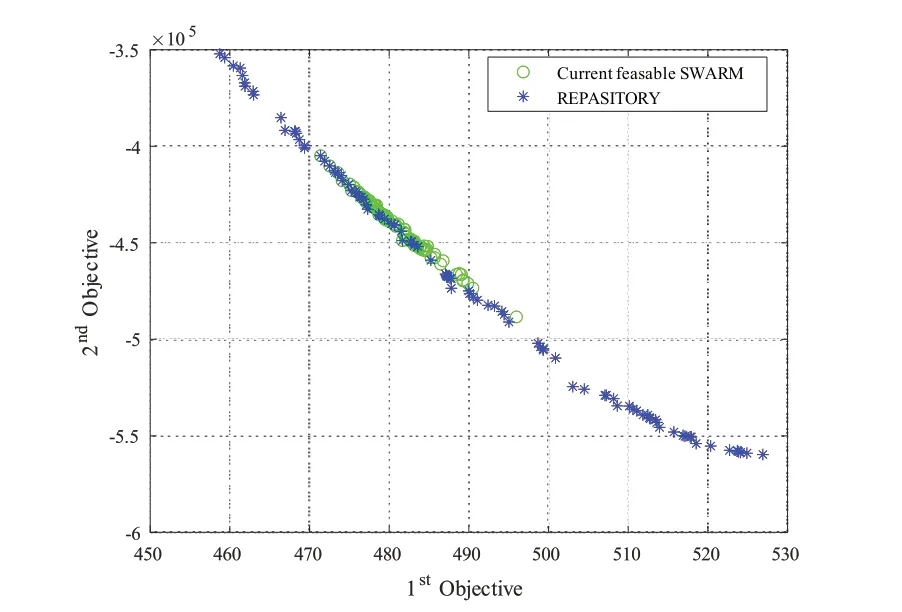
图7 帕累托最优解集

电动汽车群负荷分布如图8 所示。从图8 可以看出，8:00 ～15:00 与19:00 ～22:00 时间段内负荷需求加大，电动汽车的放电次数也在不断增加，给电网减轻了供电需求；同时电动汽车放电也给用户增加了收益。

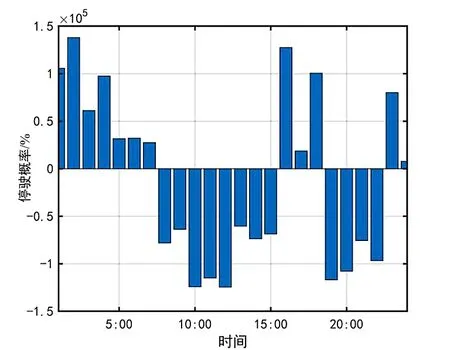
图8 电动汽车群负荷分布

基于蒙特卡洛模拟法求出无序充电方式充电功率，运用上述模型和算法求出有序充电方式充放电功率，其曲线如图9 所示。由图9 可知，相比于无序充电状态时的负荷曲线与没有进行充电时的原始负荷，电动汽车及风光发电协同调度的有序充放电行为有效平抑了负荷波动，电动汽车用户可以有效地安排充电时间，提高负荷的负载率，实现对电网的“削峰填谷”。

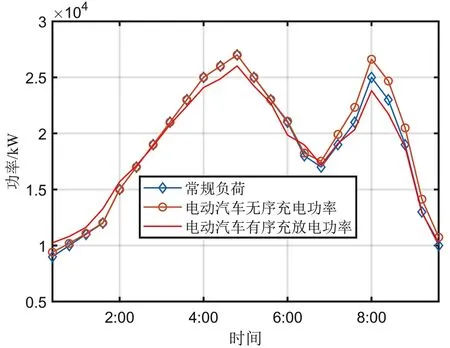
图9 有序与无序充电负荷曲线

电网的波动与电动汽车并网数量有关，如图10 所示，不同数量电动汽车并网的优化结果见表2。从图10可以看出，随着电动汽车数量的增加，负荷峰谷差越来越小。从表2可知，当电动汽车的数量为3 × 104辆时，峰谷差为1.606 × 104MW；当电动汽车数量达到5 × 104辆时，峰谷差为1.455 × 104MW，峰谷差降低了9%。由此可知电动汽车的渗透率与峰谷差呈负相关。

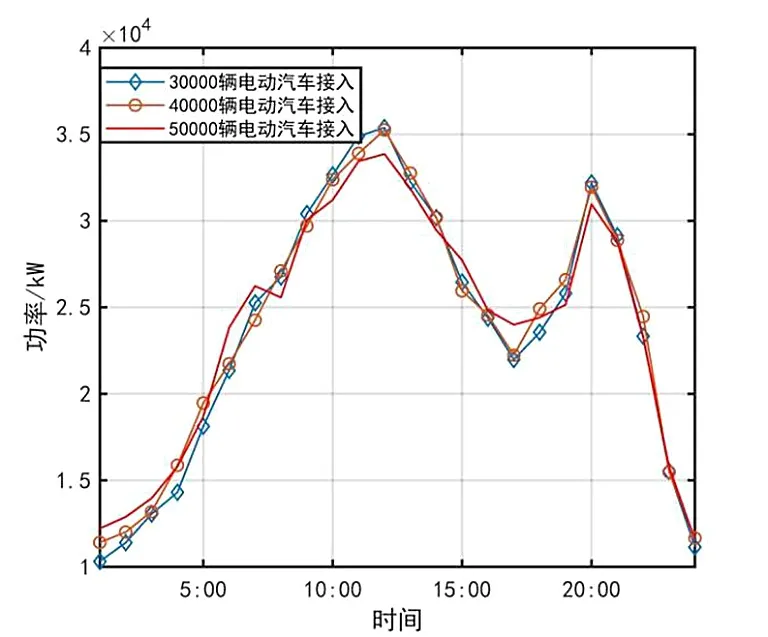
图10 需求负荷曲线对比

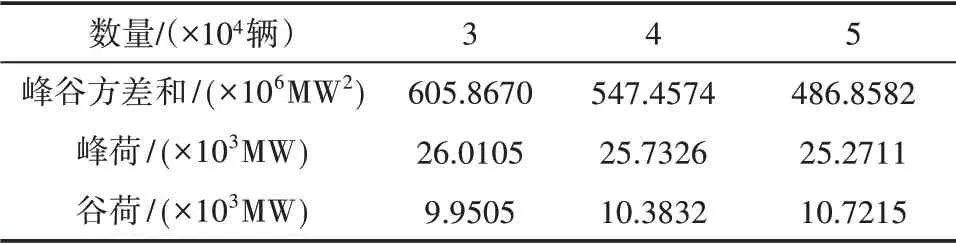
表2 优化结果对比

4 结束语

将风能和光伏为代表的清洁能源发电不断接入微电网，给电网的安全运行带了不小的挑战。通过研究风光发电及电动汽车协同优化调度模型，提出了在分时电价下无序充电和有序充放电两种模式。以日负荷均方差和车主充电成本最小为优化目标，采用MOPSO 求解模型结果，并基于选择原则在Pareto 前沿解中选取全局最优解。通过对比优化结果得出V2G 技术可以有效平抑电网波动，在用电高峰期电动汽车充当分布式电源的角色，在用电低谷期充当负荷角色。因此，优化调度模型既能够有效的降低用电负荷，又可以增加用户侧收益，实现整体多目标优化运行。