基于空间变换的随机森林算法

关晓蔷 王文剑,2 庞继芳 孟银凤

1(山西大学计算机与信息技术学院 太原 030006) 2(计算智能与中文信息处理教育部重点实验室(山西大学) 太原 030006) 3(山西大学数学科学学院 太原 030006) (gxq0079@sxu.edu.cn)

互联网、大数据、云计算与物联网等信息技术的快速发展和深度融合对机器学习提出了新的挑战，如何对收集到的大量信息进行快速准确分类，以便获取有价值的知识，成为当前机器学习领域关注的焦点之一.常用的分类算法有随机森林(random forest, RF)[1]、支持向量机、神经网络等.其中，随机森林凭借其预测准确度高、抗噪能力强、能够处理高维数据、容易实现并行化等优势，在行为识别[2]、入侵检测[3]、医学研究[4]、图像处理[5]、文本分类[6]、情感识别[7]等实际问题中得到了广泛的应用.

随机森林是Breiman在2001年提出的一种机器学习算法[1].该算法在以决策树[8-9]为基分类器构建Bagging[10]集成的基础上，引入了训练数据集随机化[11]和属性集随机化这2种随机性，使得随机森林不易陷入过拟合，且具有很好的抗噪能力.Fernandez-Delgado等人[12]对179种分类算法在121个UCI数据集上的分类性能进行了实验分析，结果表明随机森林是这179种分类算法中表现最好的.由于随机森林容易实现且性能优越，近年来受到了学者们的广泛关注[13-14].Abellán等人[15]将非精确信息增益作为属性选择的标准，建立了基于非精确概率理论的随机森林算法(credal random forest, CRF).Wang等人[16]使用2个独立的伯努利分布来简化决策树的构建，从而提出了伯努利随机森林(Bernoulli random forest, BRF).Quadrianto等人[17]提出一种Safe-Bayesian随机森林来提高随机森林的准确性和训练速度.Nadi等人[18]基于多视图理论提出一种新的随机森林算法IVRD(increase the views and reduce the depth approach in RF)，该算法通过增加决策树的数量和限制每棵树的层数来提高随机森林的性能.Wang等人[19]提出了一种在随机子空间上具有主方向的斜向森林(a forest of trees with principal direction specified oblique split on random subspace, FPDS)，其中每一棵树的分裂在随机子空间确定后都是唯一的，该算法通过启发式的方法获得超平面来保证最终森林的分类性能，避免了搜索最优分割或随机地生成分割.此外，部分学者还将随机森林算法扩展到含有高维数据[20]、不完备数据[21]、单调数据[22-23]以及少量标记样本数据[24]等复杂数据的分类任务中.

在随机森林的相关研究中，分类性能一直是一个备受关注的研究热点.Breiman[1]指出随机森林的性能高度依赖于单棵决策树的准确性以及森林中决策树的多样性.也就是说，单棵决策树的分类准确性越高，且决策树之间的多样性越大，则集成分类器的性能越好.若决策树的个体分类准确性较高，而多样性较小，那么集成分类器的性能也会受到限制.为了提升随机森林的性能，Geurts等人[25]提出了一种极端随机树算法(extremely randomized trees, ET)，通过随机选择分割测试的阈值来增加决策树的多样性.Menze等人[26]使用线性判别模型或岭回归来选择结点的最佳分割方向，构建了斜向随机森林(oblique random forest, ORF).Rodríguez等人[27]在对样本属性集进行随机分割的基础上，利用主成分分析法对分割后的数据进行特征变换，提出了基于特征变换思想的旋转森林算法(rotation forest, ROF).为了进一步增强森林中决策树的多样性，Blaser等人[28]提出了随机旋转集成算法.Zhang等人[29]将基于主成分分析和线性判别分析的旋转随机森林与标准的随机森林结合起来，形成了新的随机森林算法RFE(random forests with ensemble of feature space).该算法通过丰富森林中决策树的类型，增大随机森林的多样性，尽管森林中单棵决策树的准确性相对较低，但由于多样性增幅较大使得模型的整体性能得到有效提升.然而，该算法与其他算法相比，在构建随机森林时花费时间较多.综上可知，随机森林中单棵决策树的准确性以及决策树的多样性是2个相互制约的因素，如何在二者之间取得良好的平衡对于随机森林整体性能的提升起着至关重要的作用[30].

文献[31]在随机森林原有2种随机化的基础上加入了类别随机化，提出一种基于类别随机化的随机森林算法(randomization of classes based random forest, RCRF)，该算法为增大随机森林的多样性提供了一种新的策略，并且能够在增大随机森林多样性的同时减少对单棵决策树准确性的影响.RCRF算法从类别的角度出发，为每一棵决策树随机选择优先分类的类别，在构建森林过程中每一棵树优先对选中类别的样本进行分类.由于不同的决策树侧重的类别不同，所生成决策树的结构也不同，可有效增大基分类器之间的多样性.然而，利用该算法对某一类样本优先分类时，可能增大其他类别样本之间进行区分的难度，从而使分类准确性得不到明显改善.针对此问题，本文首先提出一种考虑优先类别的线性判别分析方法(priority class based linear discriminant analysis, PCLDA)来增强投影矩阵的针对性.与传统LDA方法的不同之处在于，PCLDA中的类间散度矩阵反映的是优先类别与非优先类别之间的关系，而类内散度矩阵反映的是所有类别之间的关系.因此，利用PCLDA方法对训练集进行空间变换，可以使属于优先类别的样本更容易被区分，同时非优先类别样本之间也尽量远离.进而，将该方法引入随机森林算法中，提出一种基于空间变换的随机森林算法(space transformation based random forest algorithm, ST-RF).在随机森林的构建过程中，通过类别随机化为每棵决策树指定一个优先类别来增加随机森林的多样性，针对包含优先类别的结点，运用PCLDA方法对样本进行空间变换来提高单棵决策树的准确性，对于不包含优先类别的结点则直接选择最优属性进行结点分裂.通过2种结点处理方式的有机结合来进一步保证森林中决策树的多样性.总之，本文所提算法ST-RF是通过在多样性和准确性之间寻求更好的平衡，来达到提升集成模型整体性能的目的.

本文的主要贡献包括3个方面：

1) 给出一种考虑优先类别的线性判别分析方法(PCLDA).该方法通过定义针对多分类问题的类间散度矩阵和类内散度矩阵，来得到更具针对性的投影矩阵.利用该方法对训练集进行空间变换，可增强不同类别的样本之间的区分效果.

2) 提出一种基于空间变换的随机森林算法.该算法能够在保证森林中决策树多样性的同时，进一步提高单棵决策树的针对性和准确性，有效提升随机森林的整体性能.

3) 利用PCLDA方法对样本进行空间变换是本文所提算法的核心思想，也是一种通用的改进策略，将该策略应用到已有的随机森林算法上，可以显著提升原算法的分类性能.

1 考虑优先类别的线性判别分析方法PCLDA

传统的LDA方法在处理多分类问题时，将所有的类别都同等对待，因此，所做的空间变换缺乏针对性.为了克服LDA的局限性，可以指定需要优先考虑的类别，并在投影时重点区分优先考虑类别的样本与其他类别样本，以增强分类的准确性.假设ωz为优先类别，为了在分类时对属于ωz类的样本给予更多关注，可以把训练集投影到一个新的空间，使得属于ωz类的样本和不属于ωz类的样本在该空间下的投影点尽量远离；同时，对于所有不属于ωz类的样本，使得在新空间中同类样本的投影点尽可能接近、不同类样本的投影点尽可能远离.为了得到具有针对性的投影矩阵，基于以上思想，在传统LDA的基础上，通过定义针对多分类问题的类间散度矩阵和类内散度矩阵，给出一种考虑优先类别的线性判别分析方法(PCLDA).与传统LDA方法的不同之处在于，PCLDA中的类间散度矩阵反映的是优先类别与非优先类别之间的关系，而类内散度矩阵反映的是所有类别之间的关系.因此，利用PCLDA方法对训练集进行空间变换，可以使属于优先类别的样本更容易被区分，同时非优先类别样本之间也尽量远离.

在多分类任务中，给定一个包含n个样本的训练集(X,Y)，X={x1,x2,…,xn}是样本集合，其中xj∈M是样本集中第j个样本，Y={y1,y2,…,yn}是与X相对应的类别标签，其中yj∈{ω1,ω2,…,ωc}是第j个样本的类别标签.

定义1.给定一个优先类别ωz和一个训练集(X,Y).将属于ωz类的样本视为正类，不属于ωz类的样本视为负类，其2类类间散度矩阵Szb定义为

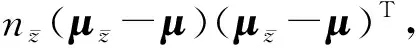
(1)

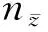
对于给定的c类训练集(X,Y)，用类内散度矩阵Sw来衡量类内样本的远近程度.

(2)

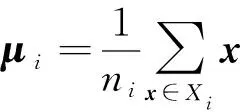
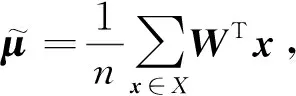
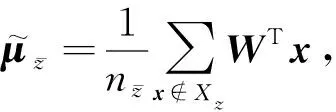
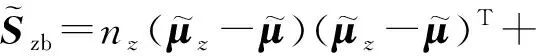
(3)

根据式(2)，可得投影后的类内散度矩阵为

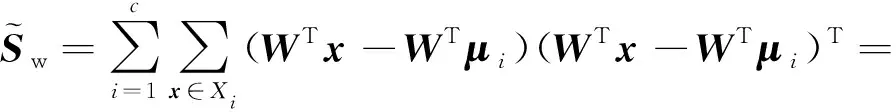
(4)

欲使同类样本的投影点尽可能接近，可以让同类样本的投影点的协方差尽可能小；欲使ωz类样本的投影点和其他类别样本的投影点尽可能远，可以使相应类中心的距离尽可能大，从而得到欲最大化的目标函数：

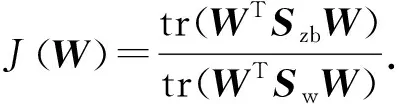
(5)

不失一般性，令tr(WTSwW)=1，则式(5)等价于

min {-tr(WTSzbW)},

(6)

s.t. tr(WTSwW)=1.

由拉格朗日乘子法，得到优化函数：

f(W)=-tr(WTSzbW)+λ[tr(WTSwW)-1],

(7)

将f(W)关于W求导，并令其为0，可得:

(8)

由于Szb与Sw均为对称阵，即：

WTSzb=λWTSw,

(9)

两边转置，可得：

SzbW=λSwW,

(10)

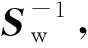
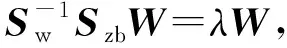
(11)

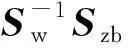
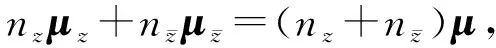
即

由上式可得：

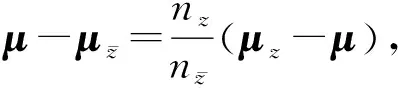
故有

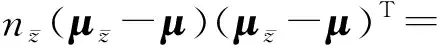
则

r(Szb)=r((μz-μ)(μz-μ)T)=
r((μz-μ)T(μz-μ))=1.

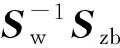
利用PCLDA对训练集进行投影时重点关注选定的优先类别，使得在投影后的新空间中属于优先类别的样本更容易被区分，同时不同类别的样本之间尽量远离.因此，将该方法引入随机森林算法中，有助于提升算法的分类性能.

2 基于空间变换的随机森林算法ST-RF

由于随机森林的分类性能主要取决于单棵决策树的准确性和决策树之间的多样性这2个相互制约的因素，为了提高随机森林的整体性能，本文将考虑优先类别的PCLDA方法引入随机森林中，提出一种基于空间变换的随机森林算法ST-RF，在多样性和准确性之间寻求更好的平衡.该算法在随机森林的构建过程中，首先通过类别随机化为每棵决策树指定一个优先类别来增加随机森林的多样性，进而针对包含优先类别的结点，运用PCLDA方法对样本进行空间变换来提高单棵决策树的准确性，对于不包含优先类别的结点则直接选择最优属性进行结点分裂.可见，ST-RF算法既能够保证随机森林的多样性，又能够提高单棵决策树的针对性和准确性，有助于集成模型整体性能的有效提升.

2.1 ST-RF算法描述

ST-RF算法的基本思想为：假设随机森林的集成规模为L，对于森林中的第i棵决策树Ti，从所有类别{ω1,ω2,…,ωc}中随机抽取一个类别标签ωz(1≤z≤c)作为决策树Ti的优先类别.决策树Ti中每个结点的分裂方式分为2种情况：

1) 当结点中包含属于ωz类的样本时，运用PCLDA方法对该结点中的训练样本进行空间变换，则数据表现形式由原来的M维降为1维，在变换后的1维空间只需根据基尼系数选择最佳分裂阈值即可生成子结点.为了充分利用训练样本的原始信息，子结点中的样本仍使用其在原始空间下的数据表示形式.

2) 当结点中不包含属于ωz类的样本时，从M个原始属性中随机选取m个属性，在原始数据空间根据基尼系数从m个属性中选择最佳分裂属性和分裂阈值生成子结点.

也就是说，ST-RF算法在训练阶段需根据每个结点包含样本所属的不同类别采用不同的分裂方式生成子结点.这2种结点处理方式的有机结合进一步保证了森林中决策树的多样性.

下面通过算法1对ST-RF算法的具体实现过程进行详细地阐述.

算法1.ST-RF算法.

输入：训练集(X,Y)、候选属性个数m、随机森林的集成规模L；

输出：包含L棵决策树的随机森林模型.

① fori=1,2,…,Ldo

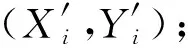
③ 从类别标签{ω1,ω2,…,ωc}中随机抽取一个类别ωz作为第i棵决策树的优先类别；

④ 创建一个包含所有训练样本的根结点；

⑤ if 结点满足停止分裂条件 then

⑥ 将该结点标记为叶子结点，其类别标记为该结点中样本数最多的类，转至步骤；

⑦ else

⑧ if结点中包含属于类别ωz的样本 then

⑨ 利用PCLDA方法对结点中的样本进行空间变换；

⑩ 在变换后的1维空间根据基尼系数选择最佳分裂阈值生成子结点；

在算法1的步骤⑤中提到的结点停止分裂条件包含2种情形：1)当前结点包含的样本都属于同一类别；2)当前属性集为空，或所有样本在所有属性上取值相同.

在测试阶段，对于测试样本x分别利用生成的L棵决策树进行预测.值得注意的是，测试样本在每棵决策树中的不同结点也要做相应的空间变换，转换到对应空间再进行属性值的判断.每棵决策树Ti都会在测试中给出一个相应的预测结果Ti(x)，L棵决策树就对应L个预测结果.随机森林最终的输出结果通过投票的方式给出，即测试样本x最终的类别标签y是得票最多的类别，具体计算为

(12)

2.2 算法时间复杂度分析

通过计算决策树中非叶结点的分裂代价对ST-RF算法的时间复杂度进行分析.具体分析过程为：

1) 当非叶结点中包含属于优先类别ωz的样本时，首先需对结点中的训练样本进行空间变换，将数据维度由M维降至1维，其计算代价为O(M3)；然后，在变换后的1维空间选择最佳分裂阈值生成子结点，其计算代价为O(n).假设当前决策树中此类结点个数为k1，则分裂代价为O(k1M3+nlb(k1)).

2) 当非叶结点中不包含属于优先类别ωz的样本时，则从属性集中随机选取m个属性，从m个属性中选择最佳分裂属性和分裂阈值生成子结点，其计算代价为O(mn).假设单棵决策树中此类结点的个数为k2，则分裂代价为O(mnlb(k2)).

由算法1可知，ST-RF算法中的单棵决策树是一棵二叉树，其结点包含2种类型：1)叶结点;2)具有2个分支的非叶结点.由于叶结点的数目至多为样本数n(即每个叶结点包含1个样本)，因此，非叶结点数至多为n-1，即有k1+k2≤n-1.综上可知，单棵决策树中所有非叶结点的总分裂代价为O(k1M3+nlb(k1)+mnlb(k2)).

由于ST-RF算法最终生成的是包含L棵决策树的随机森林，因此，本文所提算法在训练阶段的总时间复杂度为O(Lk1M3+Lnlb(k1)+Lmnlb(k2)).

2.3 空间变换策略在其他随机森林算法中的应用

利用考虑优先类别的线性判别分析方法PCLDA对样本进行空间变换是本文所提算法的核心思想，这种基于PCLDA的空间变换策略具有较好的普适性，可以将其应用到已有的随机森林算法中来提升原算法的分类性能.当在随机森林算法A上应用该策略时，首先，需为每棵决策树随机选择优先类别，进而，根据决策树结点分裂时的具体情况有针对性地进行处理：

1) 当结点中包含属于优先类别的样本时，运用PCLDA方法对该结点中的训练样本进行空间变换，在变换后的新空间根据原算法A中的阈值选择标准直接选择最佳分裂阈值即可生成子结点.

2) 当结点中不包含属于优先类别的样本时，则根据原算法A中的相应策略生成子结点.

在随机森林算法A上应用基于PCLDA的空间变换策略后，每棵决策树更具针对性，从而使得其对属于优先类别样本的区分能力增强，单棵决策树的准确性得以提升.同时，由于不同决策树随机选择的优先类别不同，保证了决策树之间的多样性，使得改进后的随机森林算法性能得到进一步提升.

3 实验及结果分析

本节通过实验对所提算法的有效性进行验证.实验环境为：处理器Intel Core i7-4790 3.60 GHz，内存8 GB，操作系统Windows 7 64位，实验中所有的算法均使用Matlab2013实现.

3.1 实验数据

本文选取了UCI和KEEL数据库中的10个数据集进行实验分析.表1简要描述了这10个数据集，包括样本个数、属性个数和类别个数.

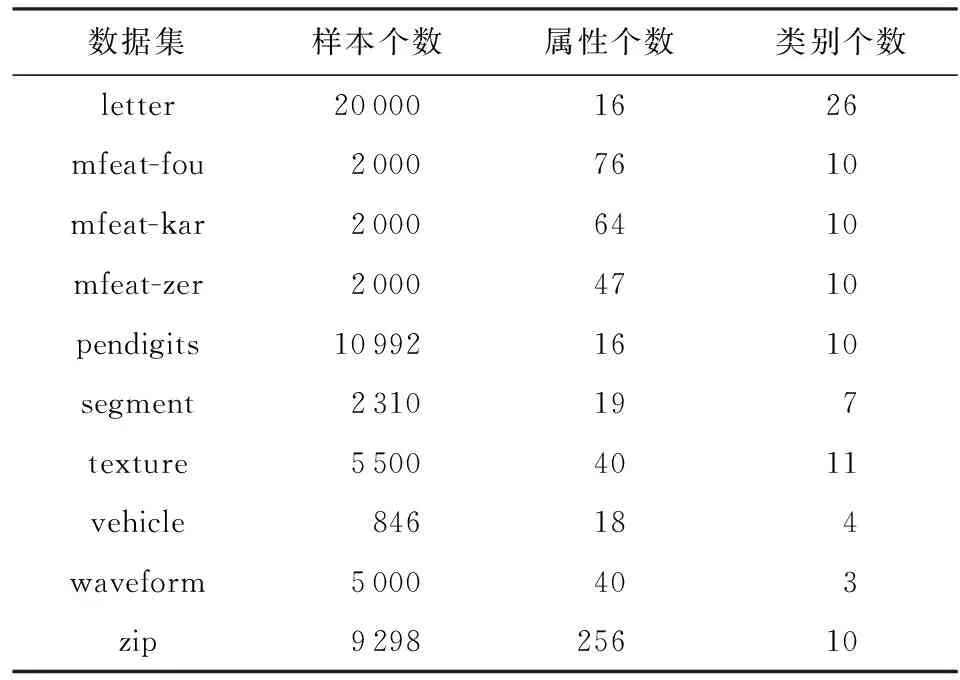
Table1 Data Sets Used in the Experiments

3.2 度量指标

实验中分别用准确率(Accuracy)、F1度量和Kappa系数κ来度量算法的性能.其中，准确率(Accuracy)表示分类器对测试集样本正确分类的数量占测试集样本总数的比例，是分类任务中最常用的性能评价指标，计算方式为

(13)

F1度量也是一种常用的分类评价指标，是查准率(precision,P)和查全率(recall,R)具有相同权重时的加权调和平均，计算方式为

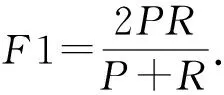
(14)

Kappa系数κ用来评估模型的分类结果与实际结果的一致性程度，也常作为分类任务的评价指标，计算方法为

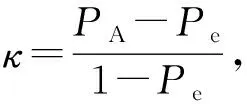
(15)

其中，PA是2个分类器取得一致的概率，Pe是2个分类器偶然达成一致的概率.

3.3 分类性能比较

为了验证所提算法的分类性能，本文将ST-RF算法与7种典型的随机森林算法RF[1]，RCRF[31]，CRF[15]，RFE[29]，BRF[16]，IVRD[18]，FPDS[19]进行对比分析.在实验过程中，各种算法的集成规模L均为100，候选属性集m=lbM.其中，BRF算法中伯努利分布参数p1=p2=0.05，结点中估计样本的最小值kn=5；FPDS算法中纯度阈值δ=1；RFE和ST-RF算法中，当类内散度矩阵Sw不可逆时，Sw=Sw+λE，λ=0.1.需要说明的是，IVRD算法是通过减少单棵决策树的深度同时增加决策树的数量来提升整体性能的，由于实验部分其他算法的集成规模都是100，为了公平起见，将IVRD算法的集成规模也定为100，并不再增加.实验采用10折交叉验证来估计算法的泛化能力，为了保证算法的稳定性，在所有数据集上将算法重复执行10次，在10个数据集上的实验结果如表2～4所示.为了进一步验证ST-RF算法的性能提升是否在统计学上具有显著性，本文使用t检验对8种算法的实验结果进行了比较，并列出在显著性水平α=0.05下的显著性分析结果，其中，Win表示ST-RF算法比其他算法性能显著提升的数据集个数，Tie表示结果不具有显著性的数据集个数，Loss表示ST-RF算法性能显著不好的数据集个数.

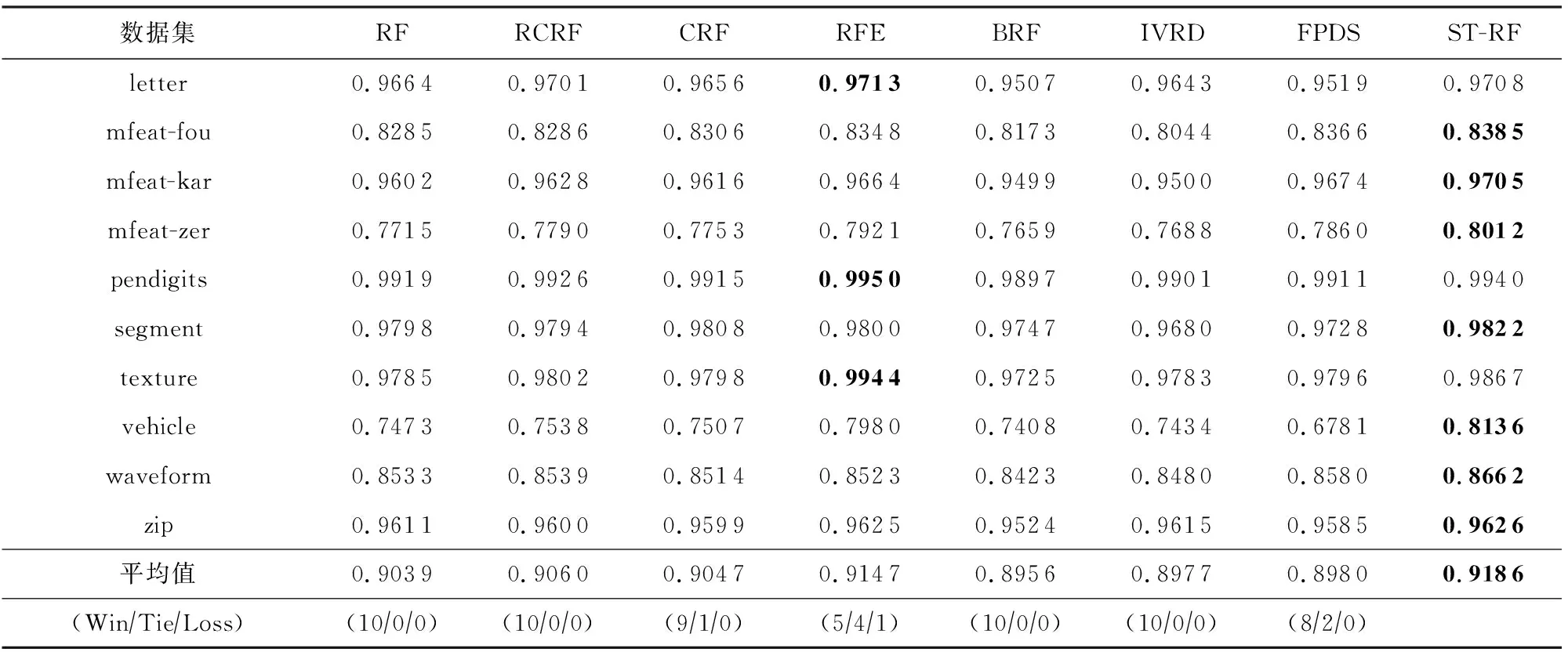
Table 2 Accuracy Comparison for Eight Algorithms

Table 3 F1 Value Comparison for Eight Algorithms

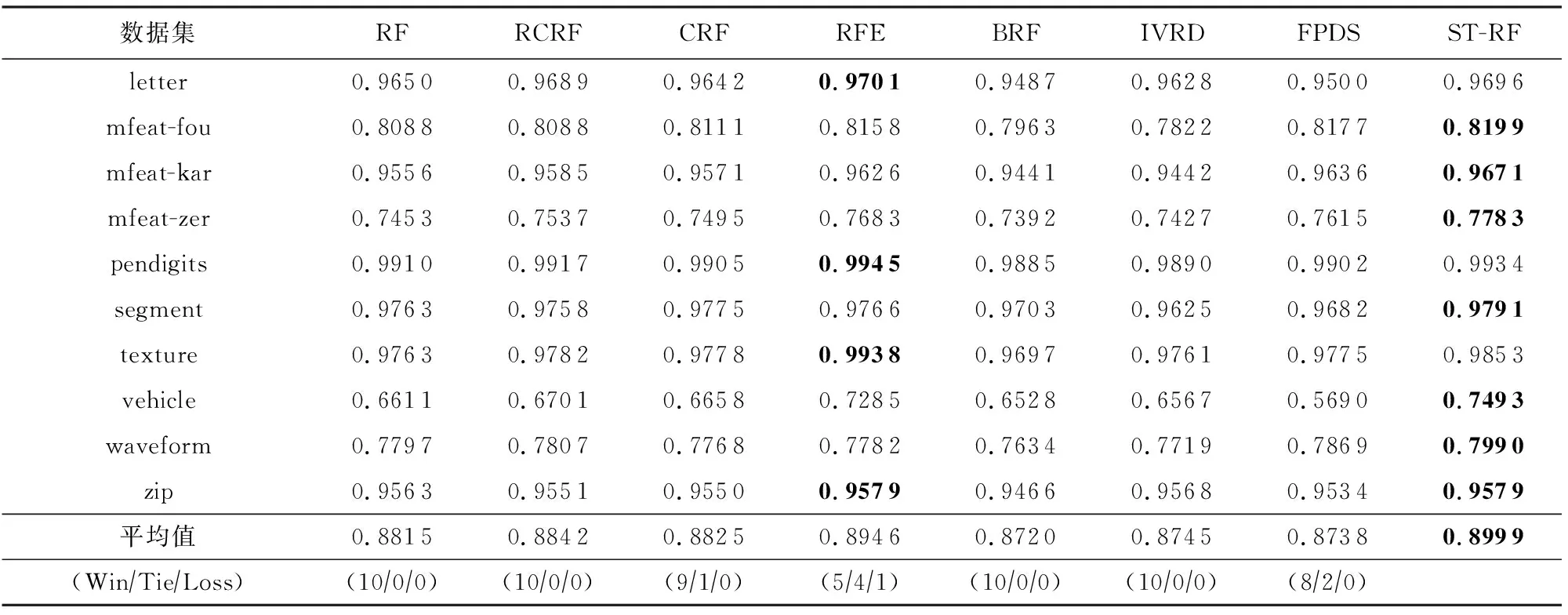
Table 4 Kappa Coefficient Comparison for Eight Algorithms

从表2～4的实验数据可以看出，ST-RF算法对所有数据集在3种评价指标上的实验结果均显著优于RF，RCRF，BRF，IVRD算法.与CRF算法相比，ST-RF算法虽然在所有数据集上性能都更优，但在segment数据集上实验结果不具有显著性.与FPDS算法相比，ST-RF算法的性能在除mfeat-fou和mfeat-kar以外的8个数据集上均有显著性优势，在mfeat-fou和mfeat-kar数据集上性能优势不具有显著性.与RFE算法相比，ST-RF算法的性能在7个数据集上均优于RFE算法，且在其中除segment和zip以外的5个数据集上有显著性优势，在letter，pendigits，texture数据集上性能略低于RFE算法，但在letter和pendigits数据集上实验结果不具有显著性.综上所述，ST-RF算法相比其他7种算法具有更好的分类性能.

在收敛性方面，文献[1]对随机森林的收敛性进行了证明，指出随着决策树数目的逐渐增多，随机森林的误差会逐步收敛.由于本文所提算法ST-RF保留了传统随机森林的基本结构，因此也具有类似的收敛性质.本文还通过实验进一步分析了随机森林中决策树的数量对算法性能的影响.以10为步长将8种算法中决策树的数量L依次从10取到100进行实验分析，实验结果如图1所示.由图1可以看出随着决策树数量的增加，各种随机森林的性能均趋向于稳定.在森林中决策树的数量较小时，ST-RF算法依然具有较好的分类准确性.

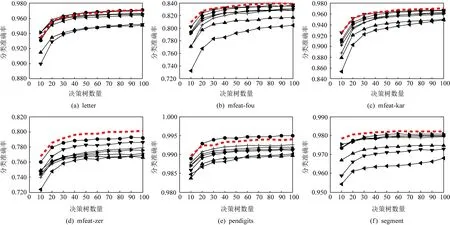
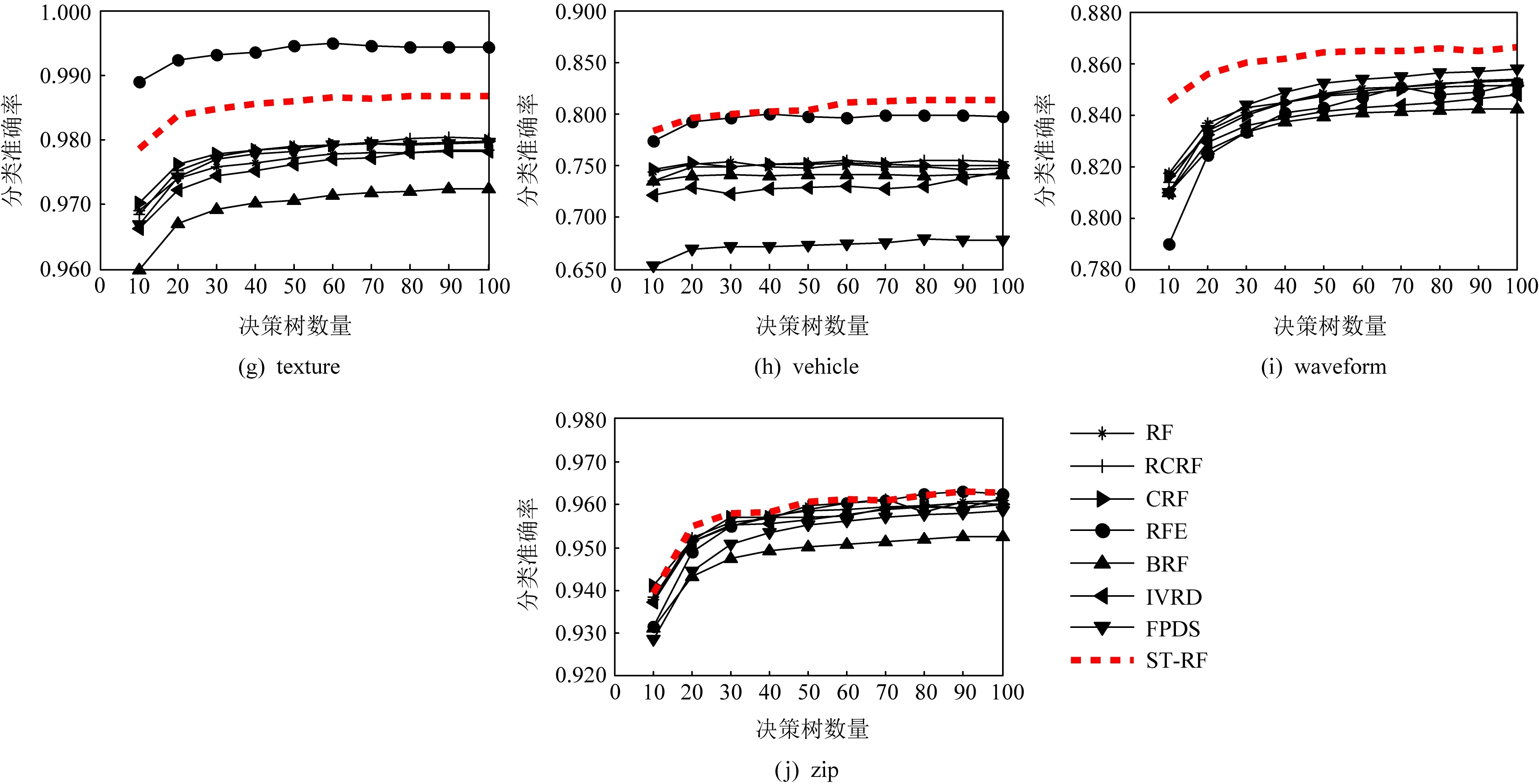
Fig.1 Influence of the number of decision trees in radom forest on the algorithms图1 随机森林中决策树的数量对算法的影响

3.4 多样性与准确性分析

通过分析ST-RF算法在多样性和准确性上的具体表现，进一步验证ST-RF算法在提高随机森林整体性能方面的有效性.首先，利用κ-误差图[27]对随机森林中的决策树进行“成对型”多样性度量.κ-误差图主要用来度量2棵决策树的差异性以及它们的平均误差，其中差异性通过Kappa系数(κ)来度量.当随机森林中决策树数量为L时，将产生L(L-1)/2对决策树，每一对决策树的度量值构成图中的1个点，点的横坐标是这对决策树的κ值，纵坐标是这对决策树的平均误差.限于篇幅本文选取了3个代表性的数据集mfeat-zer，waveform，zip，展示了8种算法在这3个数据集上的κ-误差图，如图2所示.8种集成分类器中决策树的数目L均为100，图2中每种算法的数据点云都有4 950个点.在κ-误差图中数据点云的位置越靠上，单棵决策树的误差越大，准确性越差；数据点云的位置越靠右，κ值越大，表明成对决策树的一致性程度越高，即决策树之间的多样性越小.

由图2的数据点云分布可以看出，对于数据集mfeat-zer和zip来说，RFE算法的多样性最大，但单棵决策树分类准确性却相对较低；CRF算法单棵决策树分类准确性最高，但决策树间的多样性较小；ST-RF算法虽然在多样性上略逊色于RFE，RCRF，BRF算法，但其在单棵决策树分类准确性上有了显著提高，且在与RF，CRF算法单棵决策树分类准确性相近的情况下，ST-RF算法的多样性更大.对于数据集waveform来说，ST-RF算法虽然在多样性上比其他算法小，但准确性却是最好的.由此可知，ST-RF算法相较于其他7种算法能够更好地兼顾准确性和多样性，进而实现整体性能的优化.

为了更全面地比较8种算法在准确性及多样性上的表现，表5给出了10个数据集κ-误差的均值数据.为了保证结果的稳定性，实验采用10次10折交叉验证，取10次10折交叉验证100次运算结果的均值作为实验结果.从表5的数据可以看出，在准确性方面，ST-RF和CRF算法的单棵决策树准确性比其他算法要高，其中，ST-RF算法单棵决策树错误率在5个数据集上都是最小的，CRF算法单棵决策树的错误率在4个数据集上最小.在多样性方面，RFE算法的多样性最好，其多样性在5个数据集上是最大的，RCRF和FPDS算法分别在2个数据集上多样性最大，而ST-RF算法在多样性上比其余算法要好.综合2方面来看，CRF算法单棵决策树的错误率最小，但其决策树之间的多样性也较小；RCRF算法、RFE算法和FPDS算法虽然多样性较大，但错误率相对较高.相比之下，ST-RF算法在准确性上明显更优，同时又在多样性方面比具有较高准确性的CRF算法表现更好，即ST-RF算法在多样性和准确性之间做到了较好的平衡.由此可以看出，与其他7种算法相比，ST-RF算法不仅在准确性上有较大提高，在多样性和准确性2方面的综合表现也更优，从而实现了集成模型整体性能的有效提升.

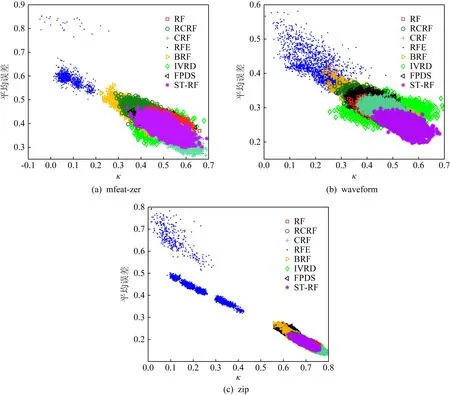
Fig.2 κ-error diagram图2 κ-误差图

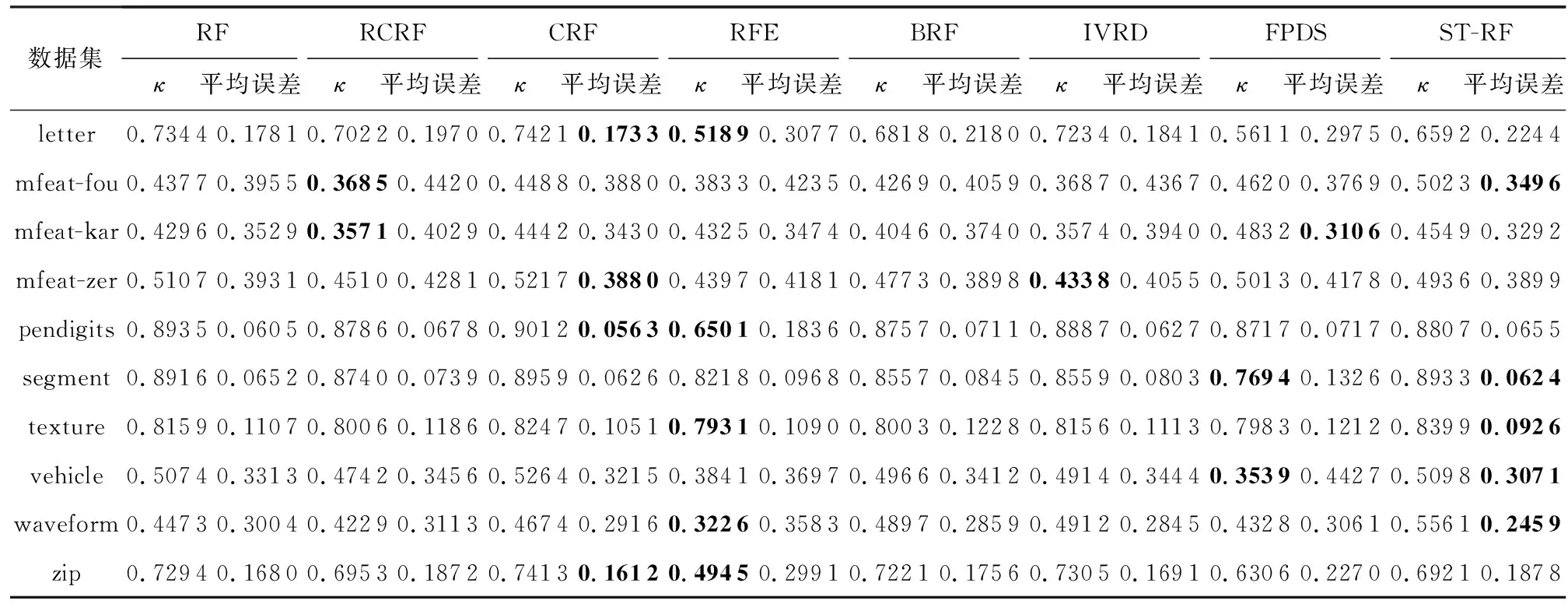
Table 5 κ-error Mean for Eight Algorithms

3.5 运行时间比较

本文还将所提算法ST-RF与其他算法从建立集成分类器所需时间和单棵决策树的结点数量2方面进行比较分析.

利用上述8种算法在10个数据集上分别构建集成分类器，集成分类器中单棵决策树的平均结点数比较结果如图3所示.从图3可以看出，IVRD算法由于深度较小，其生成的单棵决策树的结点数最少；FPDS算法生成的单棵决策树结点数最多.ST-RF算法生成的单棵决策树的结点数，在大多数数据集上和其余算法相当甚至要少.本文进一步比较了8种算法构建随机森林的时间开销.IVRD算法在构建随机森林时，每棵决策树的最大深度都要从1开始逐渐递加，直到随机森林的性能不再提升为止，因此构建随机森林的时间大大超过了其他算法，为了比较的可视化，图4仅列出了其余7种算法构建集成分类器所需时间的比较结果.从图4可以看出，FPDS算法利用PCA直接得到分裂属性，减少了属性选择的时间，因而其在大多数数据集上构建集成分类器所需时间最少.RFE算法对3种随机森林算法进行融合，构建随机森林的时间开销最大.利用ST-RF算法构建集成分类器所需时间仅在letter和pendigits这2个数据集上比RF，CRF，RCRF算法略长，但比RFE所需时间要少，而在其他数据集上建立分类器所需时间和BRF相当且远小于其他几种算法.

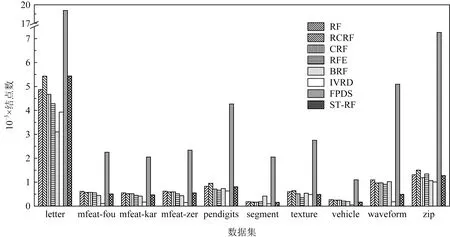
Fig.3 Comparison of node number of single decision tree图3 单棵决策树的结点数比较

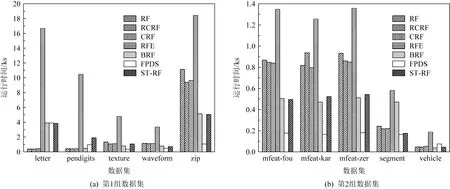
Fig.4 Comparison of the time on classifier construction for seven algorithms图4 7种算法构建分类器的时间比较

由图3和图4的实验数据可知，虽然所提算法ST-RF在结点分裂过程中引入了PCLDA方法，需要花费一定的时间计算投影矩阵，但是由于最佳投影是一条直线，投影后直接选择分裂点生成子结点，无需再从多个候选属性中选择最佳分裂属性，减少了选择分裂属性所需的时间，且投影后的样本更容易区分，从而使得单棵决策树的结点数变少，缩短了建立整个模型所需的时间.

3.6 算法普适性分析

利用PCLDA方法对样本进行空间变换是本文所提算法ST-RF的核心思想，也是一种通用的改进策略.为了验证该策略的普适性和有效性，将其应用到已有的随机森林算法上，与原算法进行对比分析.由于RF算法即是本文所提算法ST-RF的原算法，RCRF算法是在RF算法之上引入类别随机化得到的，ST-RF算法是在类别随机化的基础上又引入空间变换策略得到的，因此，在RCRF算法中引入空间变换策略得到的ST-RCRF算法即为ST-RF算法.通过表2～4可以看出ST-RF相比于原算法RF和RCRF在性能上均有明显的改善.进一步将基于PCLDA的空间变换策略分别应用到其余5种随机森林算法CRF，RFE，BRF，IVRD，FPDS算法之上，分别得到5种改进的随机森林算法，分别记为ST-CRF，ST-RFE，ST-BRF，ST-IVRD，ST-FPDS，其中，ST-FPDS算法在每一棵决策树建树之前对样本进行可放回抽样.此处仍然使用准确率(Accuracy)、F1度量和Kappa系数κ这3种评价指标对改进后的算法与原算法分别进行比较分析.实验分5组进行，改进前后的实验结果分别如表6～10所示.从5张表中的实验数据可以看出，加入基于PCLDA的空间变换策略后的改进算法在准确率(Accuracy)、F1度量、Kappa系数κ这3个指标上的性能均明显优于原算法.由此可见，基于PCLDA的空间变换策略可以作为一种通用的改进策略，来提升已有随机森林算法的分类性能.

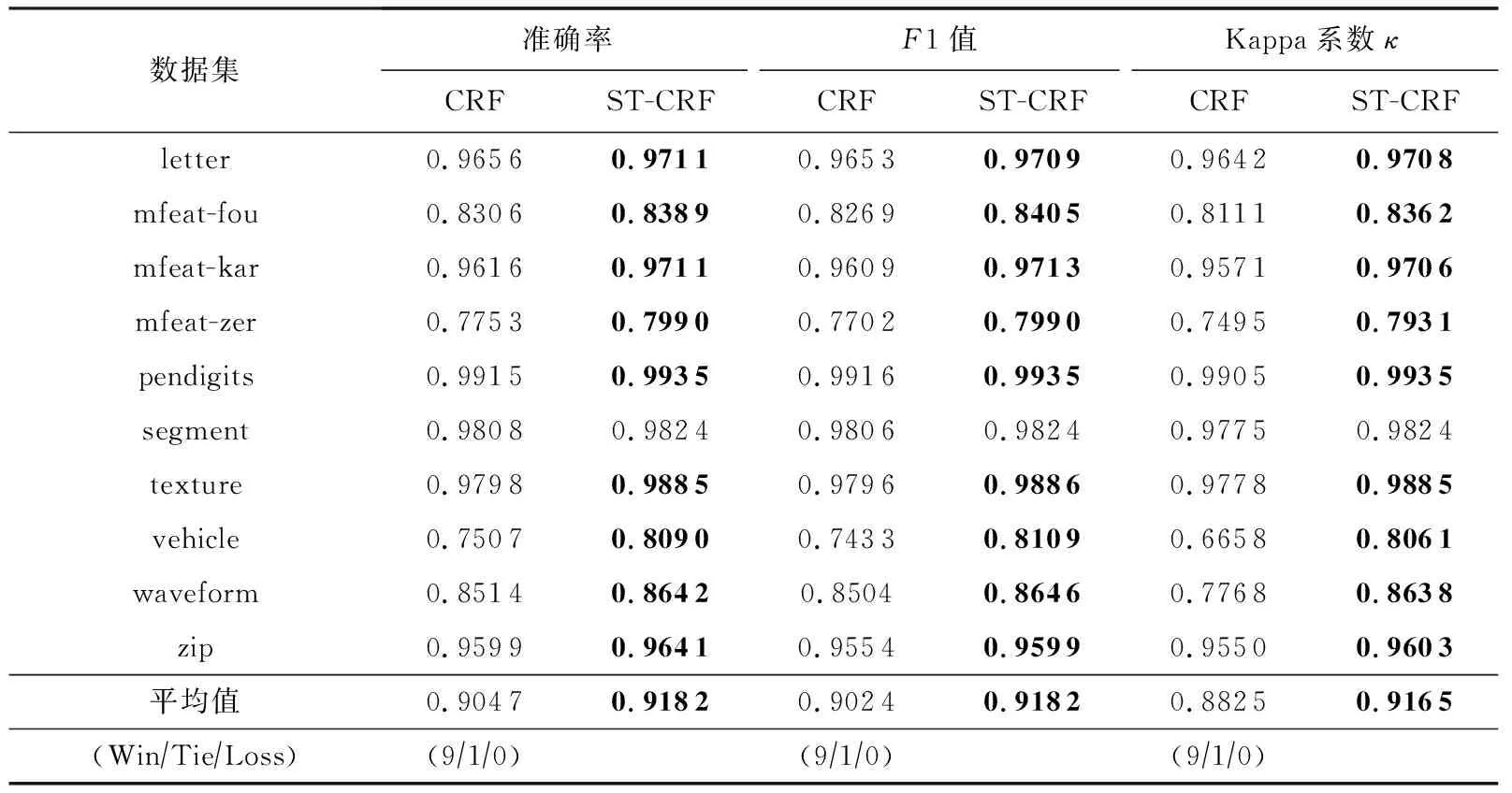
Table 6 Performance Comparison of CRF and ST-CRF

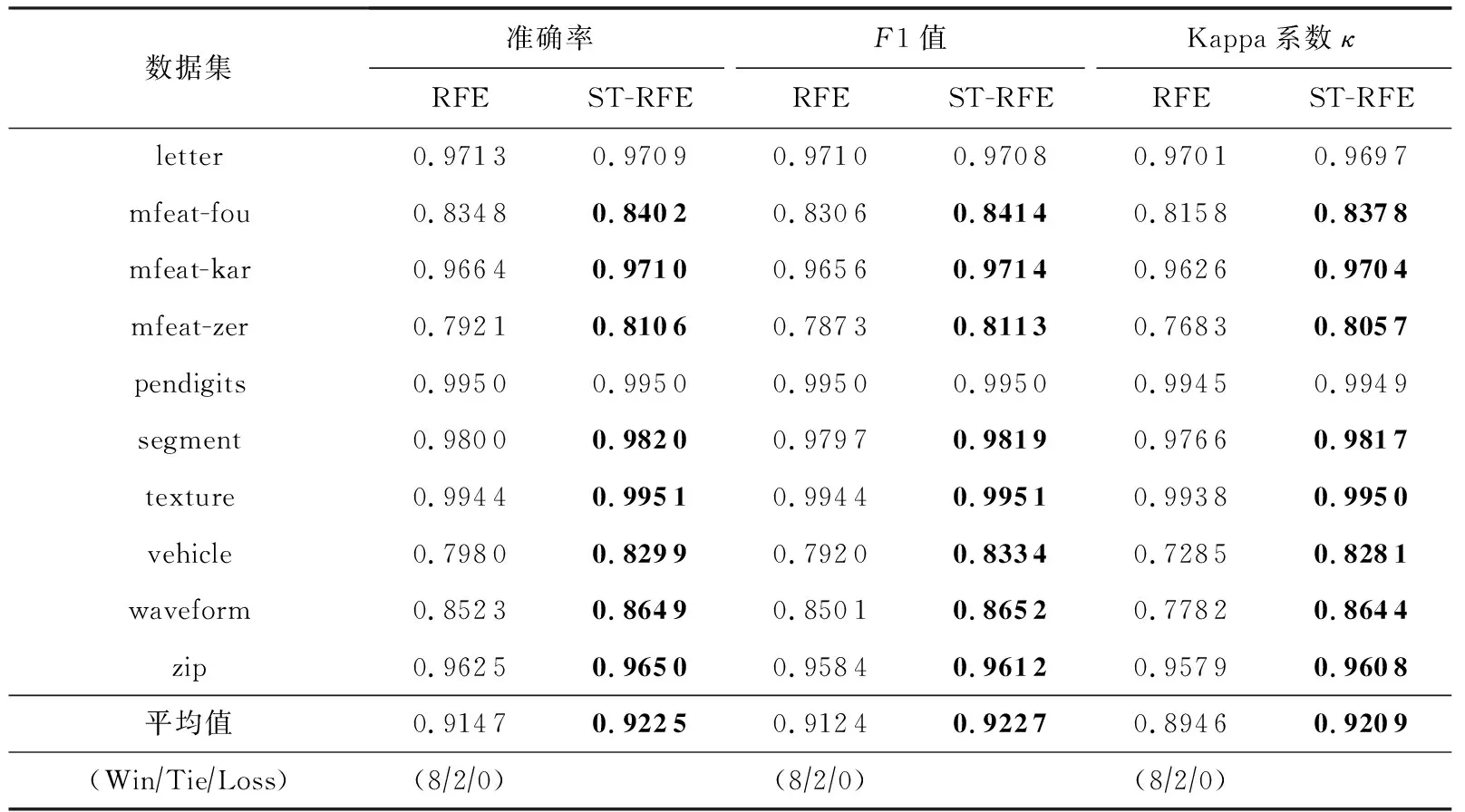
Table 7 Performance Comparison of RFE and ST-RFE

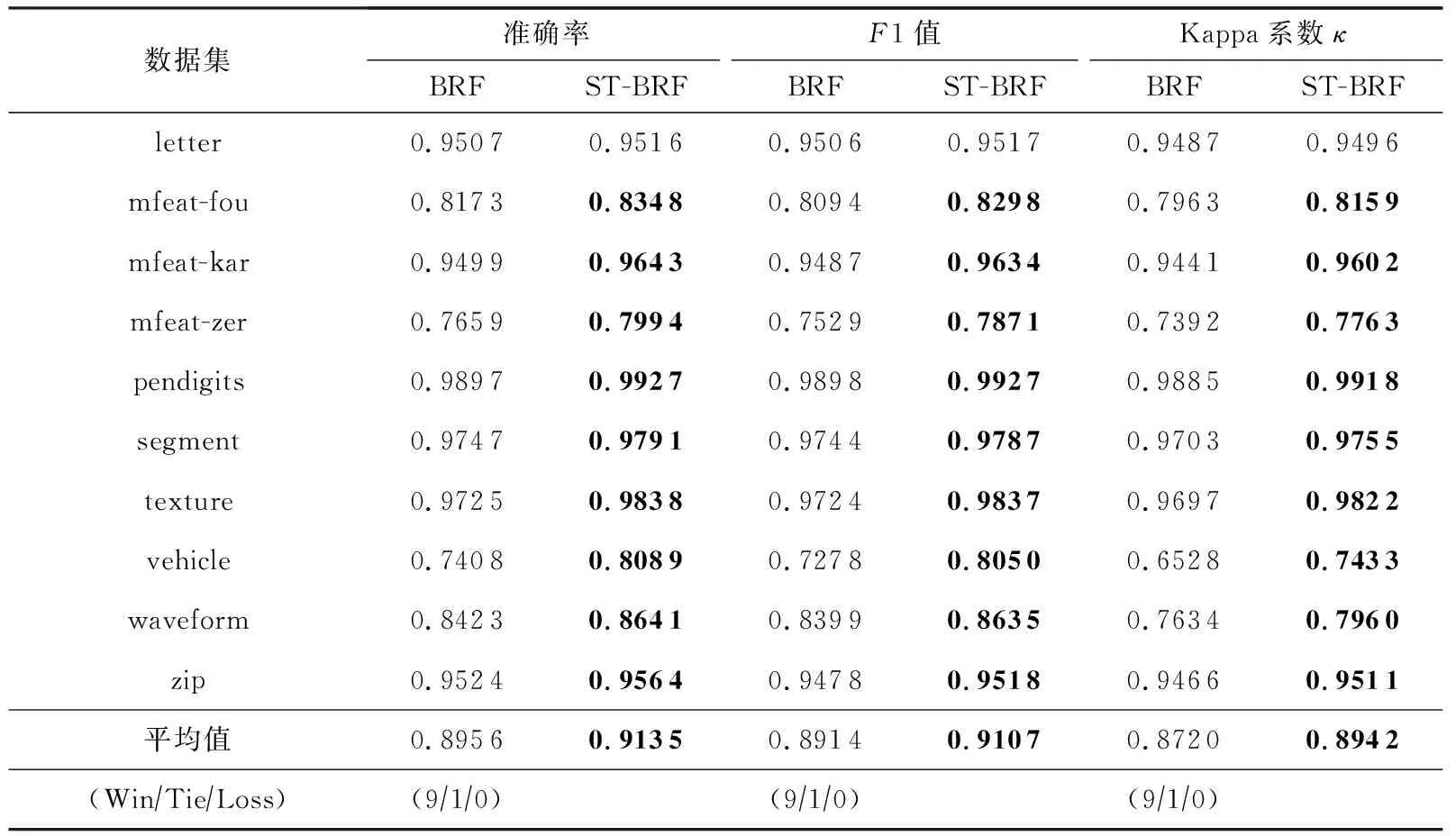
Table 8 Performance Comparison of BRF and ST-BRF

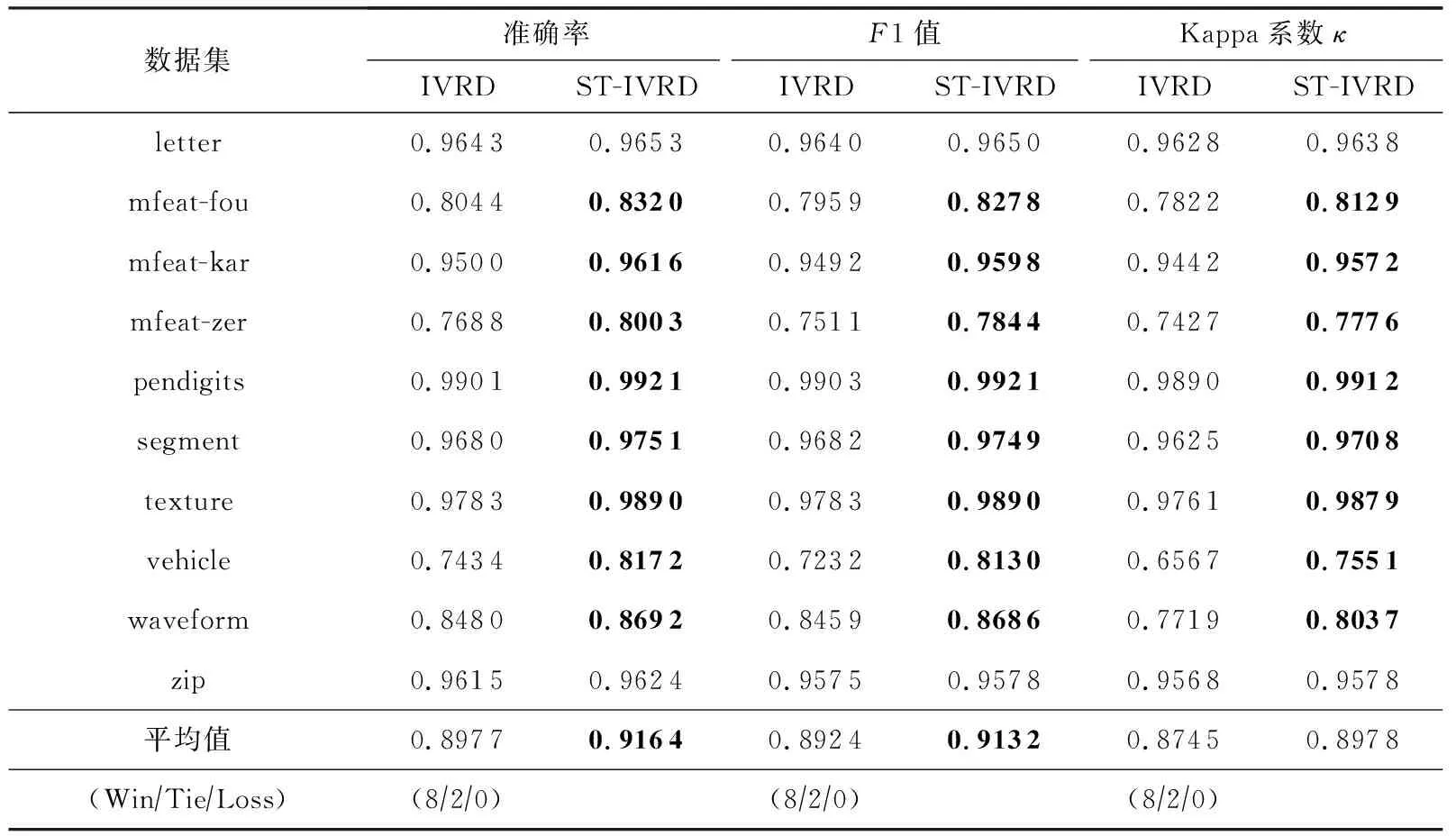
Table 9 Performance Comparison of IVRD and ST-IVRD

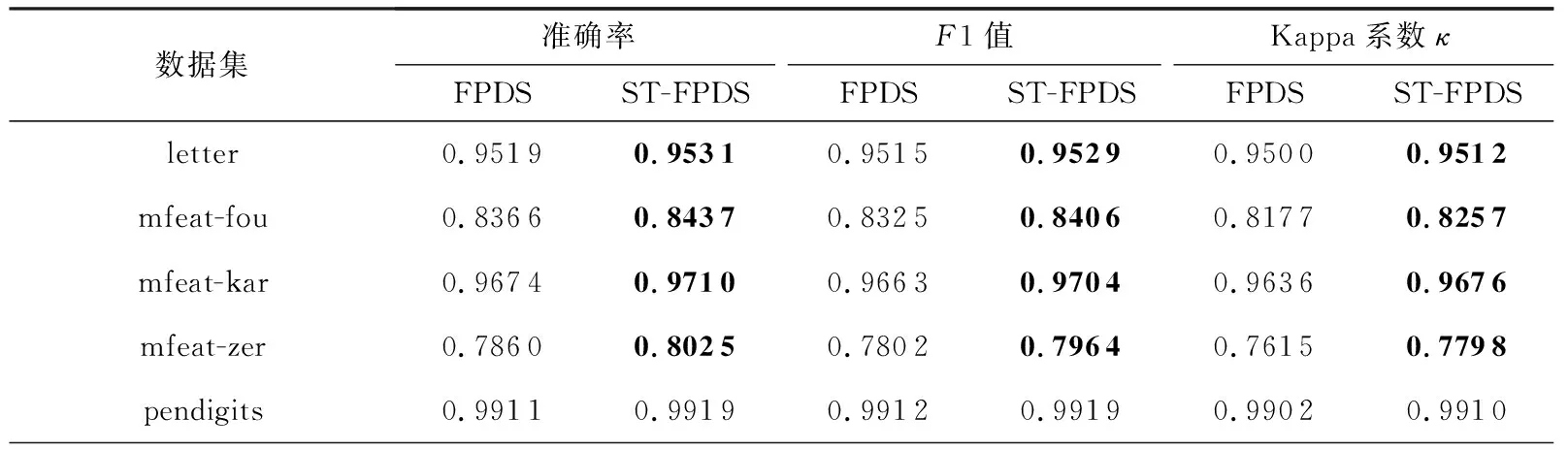
Table 10 Performance Comparison of FPDS and ST-FPDS

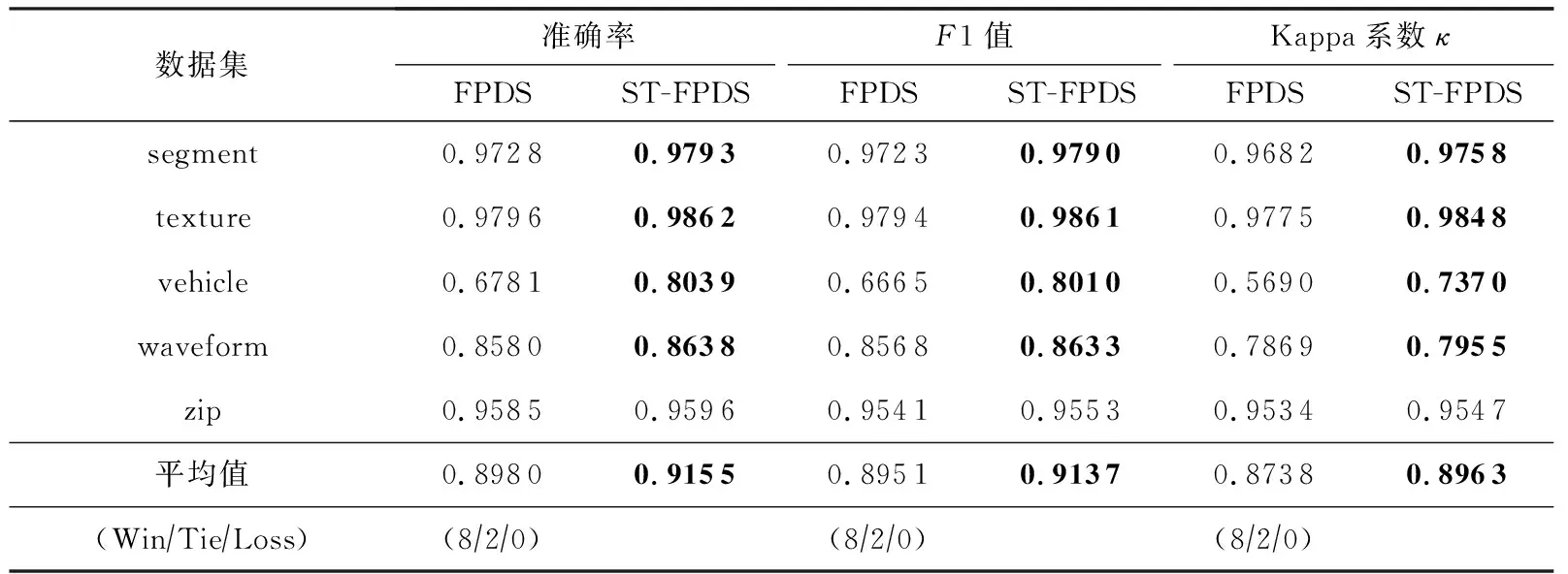
续表10

4 总 结

为了提高随机森林在处理多分类问题上的性能，本文提出一种基于空间变换的随机森林算法.该算法利用考虑优先类别的线性判别分析方法PCLDA得到具有针对性的投影矩阵，并通过空间变换提高单棵决策树的分类准确性；进而，引入类别随机化为每棵决策树指定一个优先类别，并利用PCLDA方法创建一组侧重于不同类别的决策树，达到增加随机森林多样性的目的，从而实现集成模型整体分类性能的有效提升.基于PCLDA的空间变换方法是一种通用的改进策略，将其应用到已有的随机森林算法上能够增强原算法的分类性能.未来研究将会围绕包含复杂数据类型的分类问题展开，在保证基分类器多样性的同时，提高集成模型的鲁棒性和灵活性，进一步扩大随机森林的适用范围.