基于JKR接触模型的微米级颗粒离散元参数标定
韩 伟,王绍宗,张 倩,田宇航
(机械科学研究总院 先进成形技术与装备国家重点实验室,北京 100044)
微米级粉体颗粒物质作为一种常见的工业原料,在生产应用中不可避免地涉及其仓储、 输送、 称量、 包装等过程[1-3],但是,由于部分微米级颗粒物质流动性较差,在进行仓储、 输送等过程中极易出现架桥、 搭拱、 堵结输送管路等情况[4],不利于生产活动顺利进行,因此,有必要探究此类微米级粉体颗粒物质的物性参数,准确把握其流动规律,以便于有针对性地开发相应的机械装置来解决此类问题。
近年来,在颗粒物质的物性参数、流动规律研究方面,离散单元法应用较为广泛[5]。离散单元法基于牛顿第二定律描述颗粒系统中每个粒子单元的运动状态,进而推导整个系统的流动规律,可为颗粒物质仓储、 输送、 称量等装置的设计提供理论参考。对于颗粒物质而言,开展离散元模拟的首要问题是获取物理实验难以测得的颗粒本征参数、 基本接触参数以及接触模型参数等离散元参数。目前,比较通用的方法是通过“参数标定”实验确定,其实质是建立物理实验与仿真实验之间的二阶回归数学模型,并基于某一响应值求取该模型最优解的过程,其中最优解即可视为待标定的离散元参数。针对沙土颗粒、 小麦颗粒、 蚯蚓粪基质这类粒径较大的颗粒物质,张锐等[6]、 刘凡一等[7]、 罗帅等[8]分别以堆积角为响应值展开了参数标定实验:而对于诸如面粉颗粒等粒径较小的颗粒物质,李永祥等[9]基于Feng等[10]提出的精确缩尺理论,对颗粒进行粒径放大并开展了参数标定实验;针对不同含水率的颗粒物质,Grim等[11]以堆积角为响应值,分别对干、湿颗粒的滚动摩擦系数进行了参数标定;此外,Li等[12]还研究了颗粒摩擦系数的滑板滑动实验测定方法,并进行离散元模拟验证,取得了较为理想的结果。
目前,应用离散单元法进行的参数标定实验,其对象更倾向于大颗粒物质,粒径多为毫米级及以上,即使是微米级颗粒也多进行精确缩放等操作,然而严格的精确缩放过程并不会提升计算机仿真效率,反而增加了理论计算的工作量。为了探究微米级颗粒原始尺寸下的离散元参数标定问题,本文中选取微米级粉体颗粒物质,印染行业中粒径分布在10~400 μm的一种粉体活性染料3BF Hong开展参数标定实验。由于物料堆积角能够反映物料流动特性,因此参数标定实验选用物料堆积角作为响应值。此外,实验中接触模型的选择是一个重要问题。粉体活性染料在流动过程中,由于颗粒间的粘结作用,物料流动不畅,适用于JKR模型加以描述。JKR模型即“Hertz-Mindlin with JKR”接触模型,作为一种凝聚力接触模型,JKR模型在计算中引入了颗粒间表面能的概念,可以最大程度地表征湿颗粒之间的接触特性,多用于表示湿式和细小颗粒间的粘结作用[13]。本文中应用离散元分析软件EDEM,选取JKR模型作为接触模型,对粉体活性染料3BF Hong进行参数标定实验,以实测得到的粉体活性染料堆积角角度为响应值,通过Plackett-Burman实验、 2次最陡爬坡实验以及Box-Behnken实验,推导显著影响仿真实验中染料堆积角大小的不同离散元参数与堆积角的二阶回归模型,求取回归模型最优解即为染料颗粒的离散元参数,所得数据可为后续研究颗粒流动规律,设计颗粒物质输送、称量装置提供数据参考。
1 参数测定与模型建立
选取粉体活性染料3BF Hong为研究对象,依据参数标定实验要求,测定其堆积角作为参数标定实验的响应值;并对该种粉体活性染料进行理化分析,根据其密度、粒径分布以及表面微观特征等信息建立离散元模型。
1.1 JKR接触模型
JKR模型的切向弹性接触力、切向耗散力和法向耗散力的计算基于“Hertz-Mindlin (No Slip)”接触模型理论,而法向弹性接触力基于Johnson-Kendall-Roberts理论,用法向重叠量、相互作用参数以及颗粒表面能计算法向弹性接触力为
(1)
(2)
式中:FJ为法向弹性接触力,N;E*为当量杨氏模量,Pa;R*为当量半径,m;α为接触半径,m;Δγ为接触颗粒表面能,J/m2;δ为法向重叠量,m。其中
Δγ=γi+γj-γij
(3)
式中:γi、γj分别为2个颗粒表面的单位面积粘附表面能,γij为界面表面能,当相接触的颗粒材料相同时,γi=γj且γij= 0,所以有Δγ=2γ。
JKR模型对于摩擦力的计算取决于 JKR 法向力的正向排斥部分,这与“Hertz-Mindlin”接触模型不同,JKR模型在接触力的凝聚力分量更大时,提供一个更大的摩擦力,Gilabert等[14]对强凝聚力情况下摩擦力模型修正的重要性和优势已做过相应探讨。JKR接触理论中颗粒间粘结示意图如图1所示。
1.2 堆积角的测定
参考目前广泛使用的堆积角测定方法,基于点源法设计了如图2所示堆积角测定装置,主要由铁架台、防尘罩、漏斗及堆积底座组成。对所得粉体活性染料料堆进行数字图像处理,读取料堆中部比较平直的边界,通过最小二乘法等数学手段,对边界进行拟合计算得出料堆的堆积角[15],处理过程如图3所示。
拟合直线函数斜率与堆积角角度值的转换为
(4)
式中:β为测得的堆积角;k为拟合直线斜率。经过5次实验,求得堆积角的平均值为38.57°。
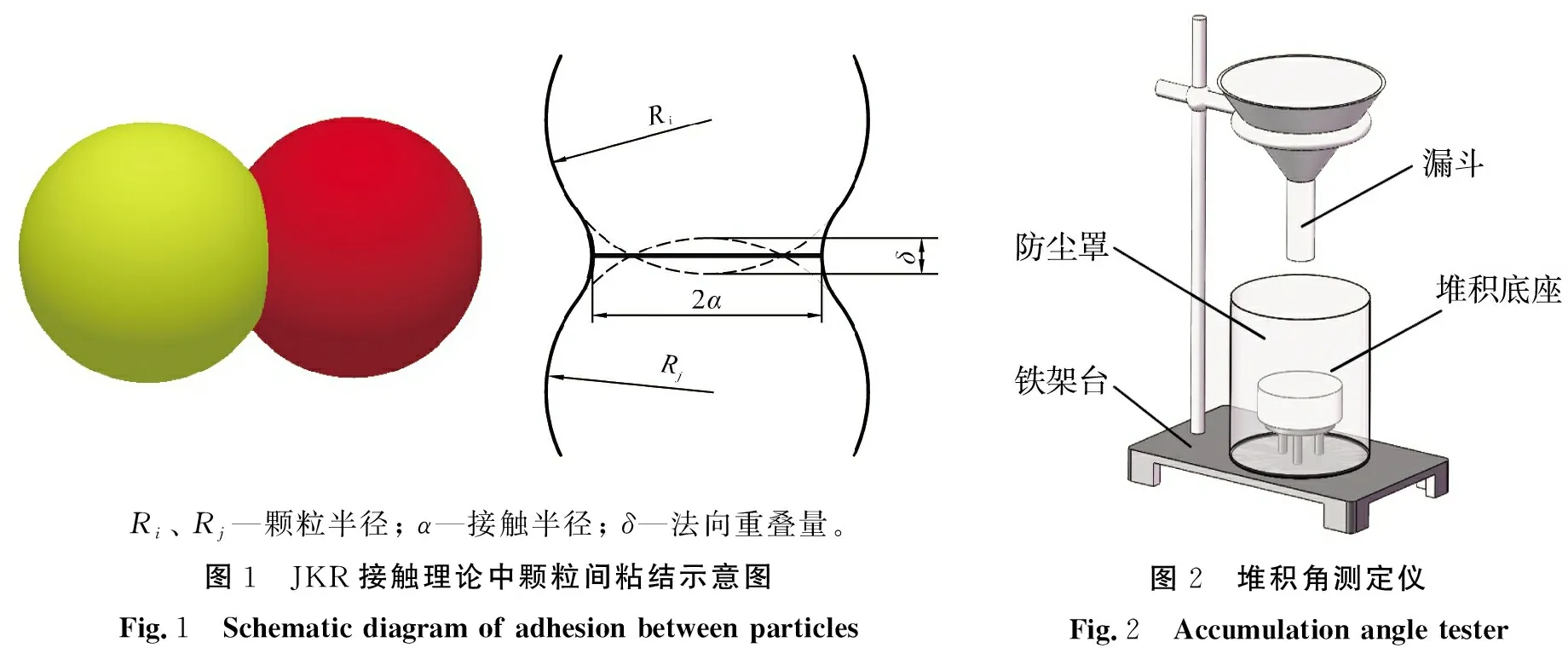
Ri、 Rj—颗粒半径; α—接触半径; δ—法向重叠量。图1 JKR接触理论中颗粒间粘结示意图Fig.1 Schematic diagram of adhesion between particles图2 堆积角测定仪Fig.2 Accumulation angle tester
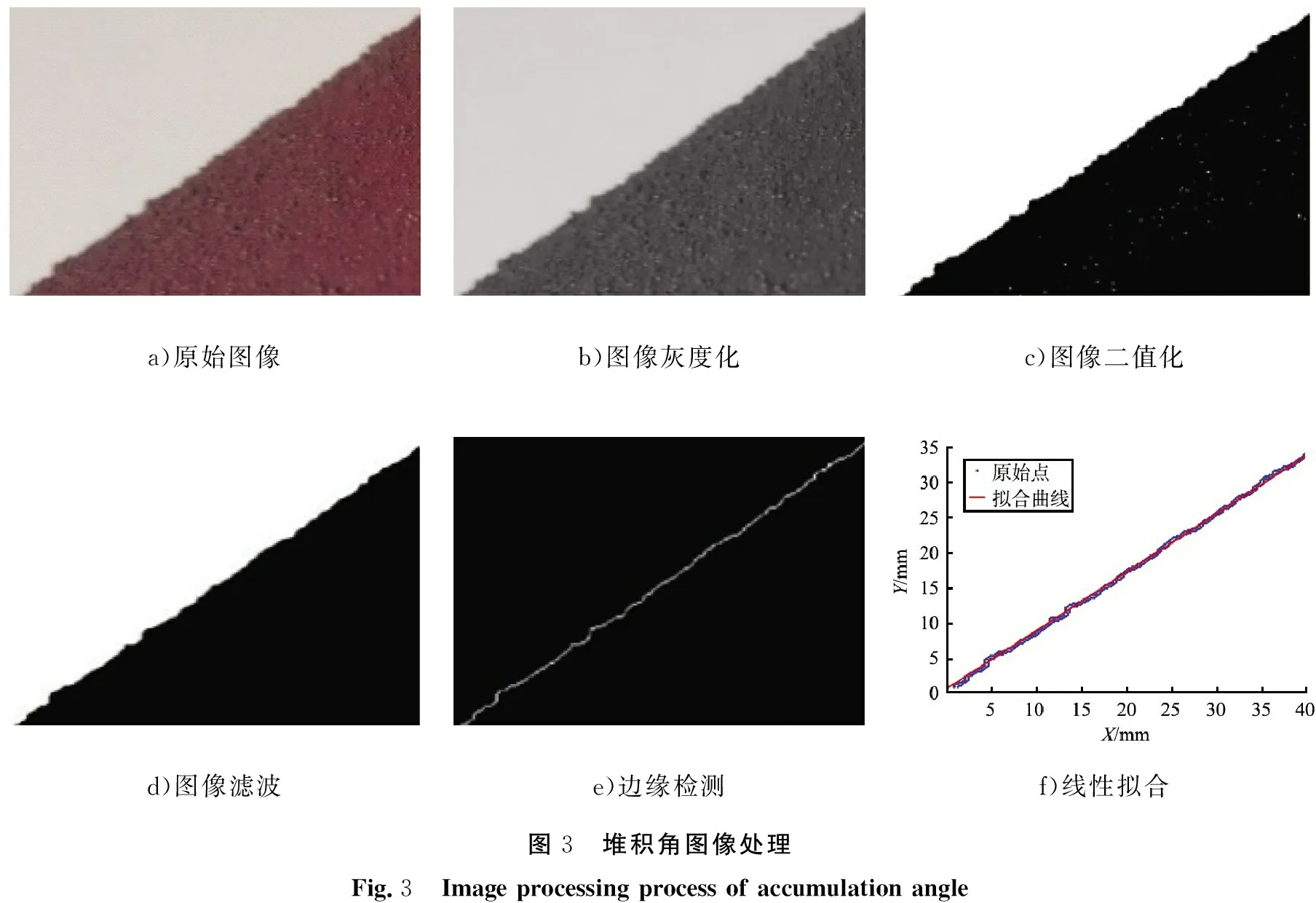
a)原始图像b)图像灰度化c)图像二值化d)图像滤波e)边缘检测f)线性拟合图3 堆积角图像处理Fig.3 Image processing process of accumulation angle
1.3 染料颗粒参数测定及离散元模型建立
经北京市理化分析测试中心测定,粉体活性染料3BF Hong的平均密度为0.570 g/cm3,颗粒粒径分布如图4所示。其中D10=42.36 μm、D50=123.09 μm、D90=229.80 μm,平均粒径为123.09 μm,体积中值直径为130.42 μm。粒径分布在45~255 μm区间的颗粒数量分数为84.66%,能够代表整个粒子系统参与计算。将45~255 μm的粒径划分为5个区间,选取代表粒径,计算所占比率,据此在软件中创建颗粒,同时结合仿真预实验确定各颗粒的生成时间及总数,如表1所示。

图4 染料颗粒粒径分布图Fig.4 Dye particle size distribution chart

表1 颗粒参数信息表Tab.1 Parameters of created particles
对染料颗粒进行显微镜拍照,得到如图5所示染料显微镜图像。由图可知,其主要由大小不均、较为完整的球状颗粒组成,偶有夹杂不规则的颗粒碎片,因此,在建立染料颗粒离散元模型时,可以使用单一球状颗粒代替染料颗粒进行仿真计算。

图5 染料颗粒显微镜图像Fig.5 Micrograph of dye particles
由于粉体物料堆积角的大小与测定仪器尺寸及待测堆积物料质量无关[6],为了简化计算,按照1∶5的比例缩放堆积角测定仪,且只在仿真软件中导入测定仪的漏斗和底座模型。按照表1给出的具体数据设置颗粒工厂,颗粒生成方式为“Dynamic”。由于不同的参数组合会对应力波在颗粒中的传播产生影响,导致各仿真中瑞利时间步不同[7],因此在所有仿真中,时间步统一取瑞利时间步的30%,网格尺寸选取为最小球形单元尺寸的2倍,为保证仿真结束后颗粒充分静止,仿真时间设定为0.8 s。待所有模型建立完成后进行后续实验。
2 参数标定实验设计及分析
参数标定实验主要包括3个部分: 1)Plackett-Burman实验,用以选择待标定因子中对堆积角影响最显著的因子; 2)最陡爬坡实验,用以确定显著性因子的最优区间; 3)Box-Behnken实验,用以建立显著性影响因子与响应值的二阶回归方程,从而求解出显著性因子的具体参数值。
2.1 待标定参数设置及显著性参数判定
目前,通过已有的研究无法直接获得染料颗粒各参数的具体范围,本文中根据EDEM软件自带的“GMEE”数据库,参考国内外文献中粉体颗粒、不锈钢材料的离散元参数设置,初步确定了待标定参数表及部分参数的取值范围,对于难以查询且受颗粒粒径、含水率影响较大的JKR 表面能数据,其取值范围由仿真预实验确定,详见表2。

表2 离散元模拟参数表Tab.2 Parameters required in discrete element methodsimulation
Plackett-Burman实验可以通过考察目标响应与各因子间的关系,比较各个因子两水平间的差异,从多个因子中选取对实验指标有显著影响的因素。故此,以染料颗粒的堆积角为响应值,设计Plackett-Burman实验,按照待标定参数显著性高低进行筛选,实验中插入2个虚拟参数K、L用于误差估计,根据表2各参数范围进行参数高低水平设置,拟定各参数的参数编码,如表3所示。

表3 Plackett-Burman实验各参数水平表Tab.3 Parameters of Plackett-Burman test
将表3各参数水平导入到Design-Expert 软件中,设置4个中心点,进行16组实验,所得Plackett-Burman实验设计及对应的仿真结果如表4所示。

表4 Plackett-Burman实验设计及仿真结果Tab.4 Design and results of Plackett-Burman test
对表4所示Plackett-Burman实验结果进行方差分析,得到各参数对堆积角的影响显著性如表5所示。由表可以看出,JKR表面能、 染料-染料滚动摩擦系数的P<0.01,对颗粒堆积角的影响极其显著;染料-不锈钢静摩擦系数的P<0.05,对颗粒堆积角的影响显著;而其余参数P值均大于0.05,对颗粒堆积角影响极小。在最陡爬坡以及Box-Behnken实验中只考虑这3个影响显著的参数。
2.2 最优区间判定
表5为各参数对堆积角影响显著性的方差分析表。由表可知,3个显著性因素对堆积角的影响效应均是正效应,因此,在爬坡实验中设定它们的爬坡步长逐步增加,其余因素选择表3所列高、低水平的平均值。设计实验方案从Plackett-Burman实验中心点开始,为了较快逼近最优值,爬坡步长取较大值,此处取步长ΔG为0.2,剩余2个参数根据Plackett-Burman 实验确定的回归模型的效应值计算得出。综合考虑参数的取值区间,经过近似优化后,各爬坡步长可确定为ΔE=0.05、 ΔJ=0.001,实验方案设计及仿真实验结果分析如表6所示。

表5 Plackett-Burman实验参数显著性分析表Tab.5 Analysis of significance of parameters in Plackett-Burman test

表6 最陡爬坡实验方案设计及仿真实验结果分析Tab.6 Design and analysis of simulation resultsof steepest ascent test
根据最陡爬坡实验,可以发现在2号水平处堆积角的相对误差较小,由1号水平到3号水平其相对误差由大变小再变大,由此可知,最优值在1号和3号水平代表的参数值之间。响应面拟合方程只在考察的紧接邻域中才充分近似真实情形,只有逼近最大响应区域后,才能建立有效的响应面拟合方程。在第1次爬坡实验后,1号和3号水平的相对误差值较大,因此,有必要进行二次爬坡实验,以便进一步缩小最优解范围。二次爬坡实验的爬坡步长设置与第1次类似,实验设计方案及结果如表7所示。由表7可以看出,2号水平至4号水平相对误差由大变小再变大,故此,可以选取3号水平为中心点,分别选择2、 4号水平为低、高水平进行后续Box-Behnken实验设计。

表7 二次最陡爬坡实验方案设计及仿真实验结果分析Tab.7 Design and analysis of simulation resultsof thesecond steepest ascent test
2.3 二阶回归方程的建立
选取显著性影响因素3个水平进行Box-Behnken实验,设置5组中心实验,实验设计及结果如表8所示。显著性参数与堆积角的二阶回归方程为
β=50.43+447.91E+121.42G+32 545.50J-155.00EG-85 200.00EJ-
20 850.00GJ-340.80E2-70.55G2-2 812 000J2。
(5)
表8 Box-Behnken实验设计及仿真实验结果Tab.8 Design and simulation results of Box-Behnken test
方差分析结果如表9所示。由表可知,交互项E×G与二次项E2的P>0.05,影响不显著。

表9 Box-Behnken实验模型方差分析Tab.9 ANOVA for model of Box-Behnken test
为进一步优化模型,除去表9中影响不显著的因素,得到显著性参数与堆积角的二阶回归方程为
β=-41.27+317.75E+106.81G+32 724.87J-85 200.00EJ-
20 850.00GJ-71.67G2-2 856 840J2。
(6)
参数优化后模型的方差分析结果如表10所示。由表可知,模型的P<0.000 1,优化模型极其显著。参数E、G、J,交互项E×J、G×J以及二次项G2、J2的P值均进一步降低,较未优化前更加显著,同时模型失拟项PL=0.128 1,拟合性较优化前有提高;变异系数CV为1.46%,模型决定系数R2为0.981,校正决定系数为0.966,预测决定系数Rp为0.903,均在合理范围之内;优化模型的实验精密度PA由25.89提高到28.57。综上,优化模型更能真实反映实际状况。

表10 Box-Behnken实验优化模型方差分析Tab.10 ANOVA for modified model of Box-Behnken test
2.4 回归模型交互效应分析
根据优化模型方差分析结果,可知交互项E×J、G×J的P值均小于0.01,影响极其显著,为探究各交互项中两参数影响预测响应值的交互效应,分别选定G为0.4、E为0.1,绘制交互项E×J、G×J的响应曲面,如图6所示。

a)交互项E×J的响应曲线b)交互项G×J的响应曲线图6 交互项E×J、 G×J的响应曲面Fig.6 Interaction effect diagram of E×J、 G×J
由图可以直观得出,当固定参数G的值不变后,在单位范围内,相对参数E,参数J的效应曲线较陡,对堆积角影响较显著,且参数J和参数E对堆积角的影响均为正效应;当固定参数E的值不变后,参数G和参数J对堆积角的影响均相对平缓,单位范围内参数J的效应曲线相对参数G的曲线较陡峭,影响更显著,两参数堆积角的影响均为正效应。同时,通过响应曲面可以得出,各因子对堆积角影响的显著性顺序为:J>E>G,这与方差分析表显示的结果相同。
3 最优参数组合确定及实验验证
应用Design-Expert软件,以物理实验实测所得堆积角度值为目标值,对优化后所得二阶回归方程求最优解,所得参数值分别为染料-染料颗粒间滚动摩擦系数E=0.075 2、 染料-不锈钢静摩擦系数G=0.493以及JKR表面能J=0.002 01,将所得参数代入EDEM软件中进行3次模拟仿真实验验证,所得堆积角图像与实测堆积角图像的对比如图7所示。
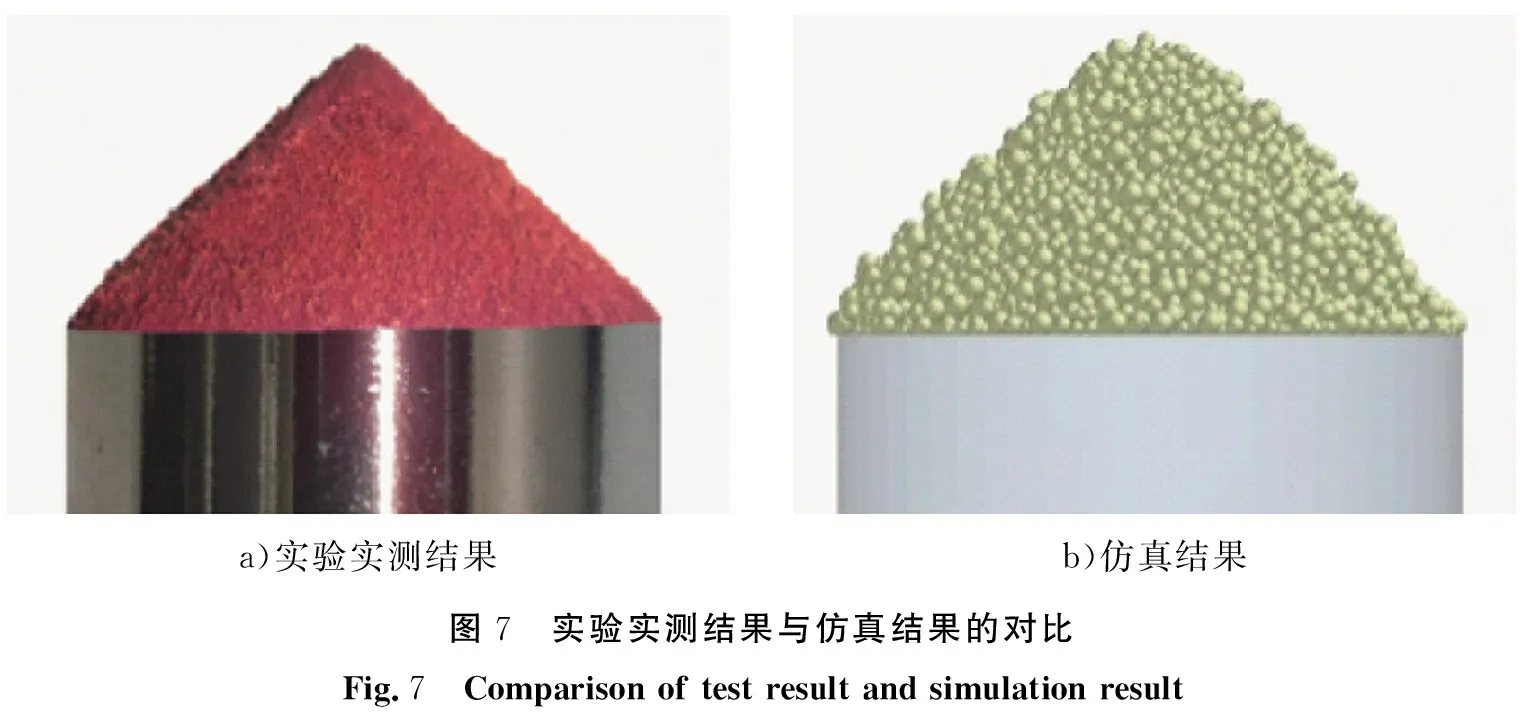
a)实验实测结果b)仿真结果图7 实验实测结果与仿真结果的对比Fig.7 Comparison of test result and simulation result
测量仿真实验所得堆积角分别为38.41°、 37.86°、 38.06°,标准差为0.278°,说明该组合参数仿真结果稳定;对仿真结果和实验实测结果进行秩和检验分析,表明仿真结果与实验实测结果无显著性差异;仿真结果平均值为38.11°,与实验实测结果平均值38.57°的相对误差为1.19%,相对误差较小,结果可靠。
4 结论
1)选择粉体活性染料3BF Hong作为研究对象进行离散元参数标定实验,通过Plackett-Burman实验得出,JKR接触模型下,影响粉体活性染料堆积角的3个显著性参数为染料-染料颗粒间滚动摩擦系数、 染料-不锈钢静摩擦系数以及JKR表面能,Box-Behnken实验得到的二次回归模型经过优化后,其方差分析结果表明该模型拟合度良好,方程拟合精确度高,可以用来预测堆积角。
2)开展最陡爬坡实验判定所考察因素的最大响应区域,若考察因素在高低水平处误差较大,为保证后续响应面拟合方程的精度,可以进行二次最陡爬坡实验降低相对误差值,以进一步提高拟合方程的精确度。
3)对优化后的二次回归模型求最优解,可得染料-染料颗粒间滚动摩擦系数、 染料-不锈钢静摩擦系数、 JKR表面能参数的数值分别为0.075 2、 0.493、 0.002 01,通过仿真验证,所得堆积角度与实测值38.57°之间无显著性差异,其相对误差为1.19%,模拟值与实测值之间误差较小,因此判定此实验标定的粉体活性染料颗粒离散元参数是可靠的,应用离散单元法进行微米级颗粒的离散元参数标定是可行的。

