仓配一体化仓库拣货路径优化策略应用研究

闫 军，王璐璐，常 乐

（兰州交通大学 机电技术研究所，兰州 730070）

0 引言

近几年，电子商务的快速发展使仓库效率成为一个热点话题，由于商品流通规模的不断扩大，仓配一体化[1]逐渐成为物流行业的一个发展趋势。在普通仓库的所有作业中，经研究发现，拣货作业就占用60%，货物移动成本占大约90%，拣货作业时间至少占其全部作业时间的35%。故如何提高仓库内部工作效率、降低成本成为仓配一体化企业越来越的关注问题，仓库内货物的拣选路径优化研究也成为一个热点问题。本文以西北某仓配一体化企业为研究对象，对货物拣选路径优化问题进行研究。

目前，针对仓库货物拣选路径问题的研究，学者主要围绕S型拣货路径策略（穿越策略）、中点穿越策略、返回策略、最大间隙策略、混合策略以及最优路径策略等几种策略进行研究。常用研究算法有：遗传算法、模拟退火算法、蚁群算法等。

国外学者Hall.R.W[2]在文章中通过分析S型拣货策略、返回策略以及最大间隙策略，得出如果将三种策略进行有效结合，可以提高拣货效率，从而提出混合型拣货策略。Lu,Chen[3]等将仓库货位分配和自动存取交叉问题进行综合研究，以启发式算法和禁忌搜索算法相辅相成作为优化过程。Chen-Yang[4]等在研究多品种、少批量情况下的货物时，以拣货批量及拣货路径为研究重点，采用蚁群算法和粒子群算法两者结合的混合算法，求解最佳拣货批量的拣货路径问题。Yang C L[5]等考虑到货物的特征、相关存储的限制，以分类存储策略为基础，运用聚类分析方法中的主成份分析方法，得出货位检索时间相比之前提高33%。Chabot T,Coelho L C[6]等针对狭窄通道的仓库，结合工厂的实际情况，建立3D模型，运用启发式算法对拣货作业的路径及行走距离进行求解，使拣货人员在仓库中的总行走距离达到最小。

国内学者穆聪聪[7]等研究在单区仓库中，产品频度与偏离度对货物出入库货位分配策略的影响，将出入库频率高的货物分配在离出入口较近的货位上，货物在出库时采用偏离度的优化策略，快速完成拣货作业，有效提高拣货效率。房殿军，彭一凡[8]等针对多巷道仓库，对多条横向通道拣货路径进行研究，提出一种组合式启发式算法可以有效提高拣货作业效率。杜颖[9]在动态货位指派与拣货路径系统优化研究一文中，提出货位与拣货协同作业的拣货方式。根据市场变化，达到存拣合一，有效提高拣选人员的工作效率。

本文研究的是仓配一体化仓库拣货路径优化策略应用研究，在库存策略不变的条件下，结合仓配一体化实体仓库信息建立拣货路径优化模型，将遗传算法、遗传模拟退火算法的运行时间、距离以及收敛度进行比较，得出不同水平下算法的优劣程度。

1 仓配一体化仓库拣货路径优化模型概述

1.1 建立仓库二维坐标系定义货位坐标

西北地区某仓配一体化仓库平面图如图1所示：一个仓库主要分为两个区，可看作双区型仓库，仓库两个区中有储存货物的若干个货架，在仓配一体化仓库内建立平面坐标系，根据双区型仓库内部给定的编码确定货位，且每一个货位只能存储一个SKU，再确定该货位对应的坐标。

图1 仓配一体化仓库平面示意图

如图1所示，在仓配一体化双区型仓库里，包括三条过道和多条拣货巷道。现以仓库左下角O点视为平面坐标系中的原点坐标，O点向右为x轴正方向，O点向上为y轴正方向。假设左下角距离原点的地方有一点S，其坐标为（xs，ys）。假设库内货架的间距宽为hc，两排货架合并起来宽度为2hc，当拣货员进行拣货时，经过每个货位的中点即为拣货员行走的路程[10]。设仓库中某一货架对应货位的坐标为W（x，y），则货位横坐标为：

C为仓库货架的巷道数。

如图1所示，假设仓库中任一货位距离S点的纵向距离为Y，则该货位的纵坐标为：y=Y+ys。

假设在一列货架中，每排货架对应的编号为B，即货架最大编号为Bmax，货架长度为D2，两货架之间的间隔为D1，在忽略货架立柱的影响下，每节货架的内部长度为ln，若在长度为ln的货架上安排Pmax个货位，则每一个货位对应的长度为lnp，几个参数之间的关系如下：

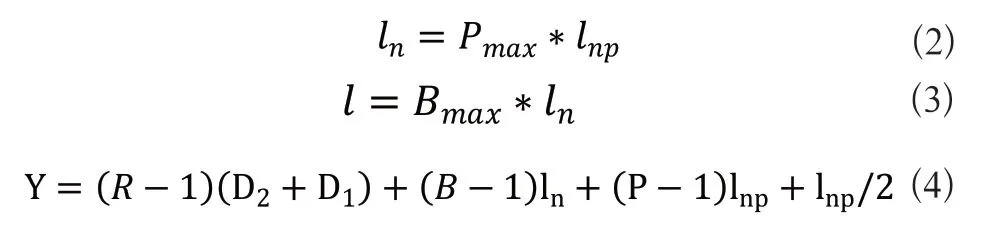
即仓库中货位的纵坐标为：

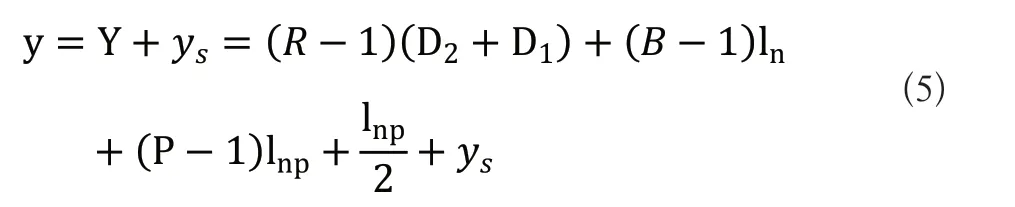
根据式(1)～式(5)可以得出仓库中任一货位的坐标。

1.2 根据坐标生成距离矩阵

当接到客户订货单，生成波次拣货单时，所拣货物的货位已确定，仓库拣货人员根据波次拣货单进行播种式拣货，将每批订单上的同类货物先累加然后拣取，集中搬运到统一的分拣场所，然后再根据每个客户所需货物的数量进行二次分拣，直至所有订单拣取完成。在分拣过程中，根据货位编号建立距离矩阵。

假设仓库中有两个货位分别为S1（x1，y1），S2（x2，y2），且二者之间的最短行走距离为D12，设：

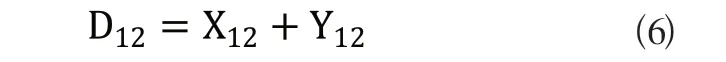
式中：X12为两货位间行走最短折线路径的横向长度总和；Y12两货位间行走最短折线路径的纵向长度总和；（i=1,2）为仓库某一货位Si（xi，yi）当前位置距离货架最右边的距离，即：

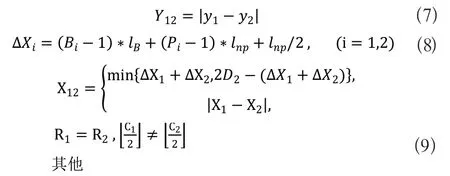
式(8)表示任意两个货位S1和S2之间最短路径的纵向距离的总和为两坐标点的纵向距离。式(9)表示当拣取的两个货位为同一区不同巷道时，拣货人员会绕过货架行走，取向左和向右行走的较小值，其他情况则表示拣货人员不存在绕行的情况。Si表示货位，Dij表示两货位之间的最短距离，N表示拣货总量，由此可以得到仓库内任意两个货位间的距离矩阵，如表1所示。

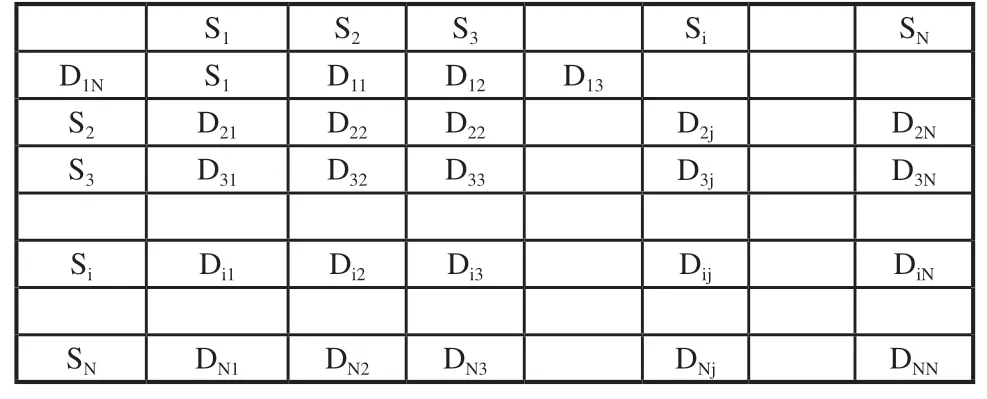
表1 货物间的距离矩阵

2 模型假设

假设TSP模型建立如下：

现假设拣货员手中持有一个波次的拣货单，从起点S0（0,0）点出发拣货，当拣选完一个波次的货物后再回到起点，这一拣货过程遍历的所有SKUs所在货位分别记为S1,S2,…,Sn，且货位与货位之间两两互不重复。所有SKUs的货位坐标表示为Si(xi,yi),i=1,2,…,n。假设货位Si和Sj之间的最短距离为Dij，在此基础上引入参数dij，（i=0,1,2，…,n,j=0,1,2,…,n）表示得意义如下所示：

对于距离及参数，有以下条件：Dij=Dji，且di0=d0i=Di+yi。待拣货位至仓库出入口的距离矩阵如表2所示。

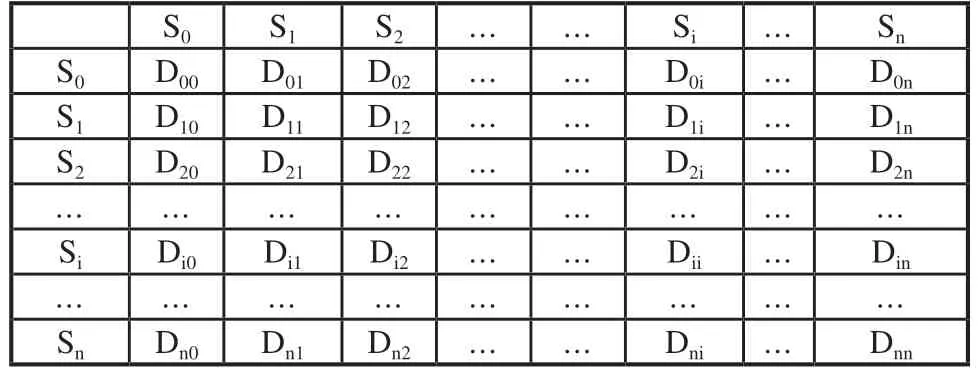
表2 待拣货位至仓库出入口的距离矩阵

3 模型构建

一般传统低效率的拣货方式是拣货人员根据平时积累的经验以及根据货物按照巷道顺序的记忆进行拣取，当某一波次的订单生成，由于未对被拣货物拣取路径顺序进行优化，使得不同货物在拣取时均采用同一模式，导致货物拣选效率不高，故采用混合遗传模拟退火（GASA）算法来优化拣货路径。

现以拣货人员在仓库中行走的最短拣货路径为目标，可建立如下数学模型：

式(10)表示从起点出发途经n个货位后回到起点的最小化的总路径长度，式(11)和式(12)表示拣货路径经过货位的次数恰为一次，式(13)表示拣货路径经过所有货位构成一个完整的回路。式(14)表示变量为0-1变量约束。

4 算法求解与案例分析

4.1 算法求解

本文将拣货路径问题等同于NP-hard问题，传统意义上一般采用S形启发式算法来求解。遗传算法（GA）在运行的过程中只着重于局部，在算法进行优化时只考虑遗传算子的变异率和交叉率等参数的变化，很容易陷入“早熟”，对于大规模计算量的问题已经不能很好地解决。混合遗传模拟退火算法（GASA）[11]是模拟退火算法在遗传算法的基础上针对遗传算法局部限制的情况下，结合模拟退火局部寻优融合而成的一种算法。本文分别采用遗传（GA）算法、遗传模拟（GASA）算法对案例进行分析与求解。

模拟退火算法是在蒙特卡洛思想设计的基础上近似求解最优化问题的一种方法。其算法流程如图2所示：

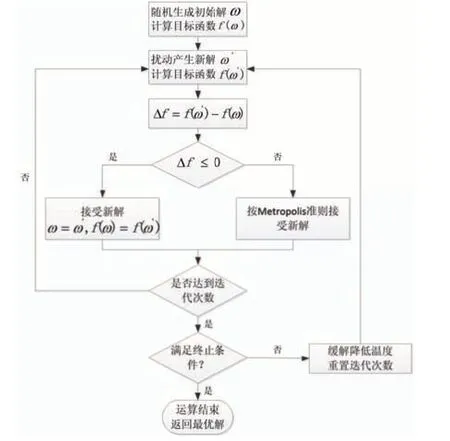
图2 模拟退火算法流程图

4.2 案例分析

以西北某仓配一体化中心为案例背景，在仓库拣货人员接到拣货单后，假设拣货单上有30个待拣货物，拣货人员在仓库中的平均行走距离为1.3m/s，巷道宽度为1.4m，通道横向宽度为2.8m，操作员在对拣货单进行扫描等一系列初始化的动作所花费的时间为2s，拣货人员拣取货物所花费的时间为1.7s。

1）基于遗传（GA）算法求解

当采用遗传算法对30个货物进行有效拣选时，拣选的最优路径顺序为：0-1-27-28-29-26-25-24-15-14-8-10-21-20-19-7-11-9-18-3-2-6-5-4-13-16-17-22-23-12-30-0，总拣货距离为：505.8162m，总拣货时间为442.09s。拣货路径示意图如图3和图4所示。

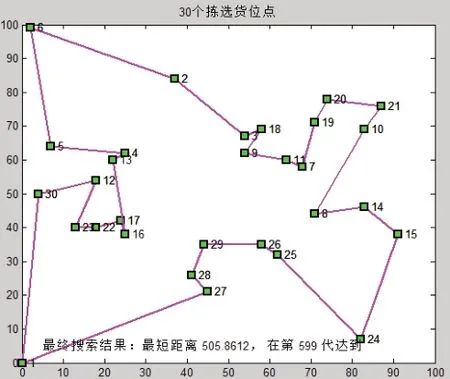
图3 GA算法路径示意图

图4 GA算法拣货路径

2）基于遗传模拟（GASA）算法求解

当采用遗传模拟算法对30个货物进行有效拣选时，拣选的最优路径顺序为：0-16-17-22-23-12-13-4-5-30-6-2-9-3-18-20-21-10-19-7-11-8-14-15-24-25-26-29-28-28-0，总拣货距离为：502.7799m，总拣货时间为439.75s。拣货路径示意图如图5和图6所示。

图5 GASA算法路径示意图

图6 GASA算法拣货路径

3）不同规模下拣货单的对比

采用GA算法和GASA算法分别在拣货数量为30、50、75的情况下进行对比，结果如表4所示。由表4分析得，随着拣货数量的增加，完成平均每张拣货单的距离和时间会逐渐增加。

4）结果的对比及分析

由表3、图7和图8可以看出，GASA比GA更适合求解这类问题，以拣货路径和拣货时间为例来说明，GASA求解的结果均小于GA，两算法的最优解均低于平均解，GA迭代次数达到599时，目标函数基本上达到最优；GASA迭代次数达到576时，目标函数基本上达到最优。从拣货路径来看，GA使用了505.8162m，GASA使用了502.7799m，路径节约了0.6%，从拣货时间来看，GA使用了442.0900s，GASA使用了439.7500s，时间节约了0.5%。

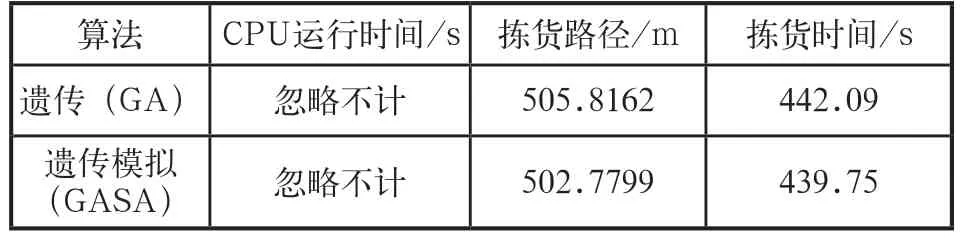
表3 算法对比

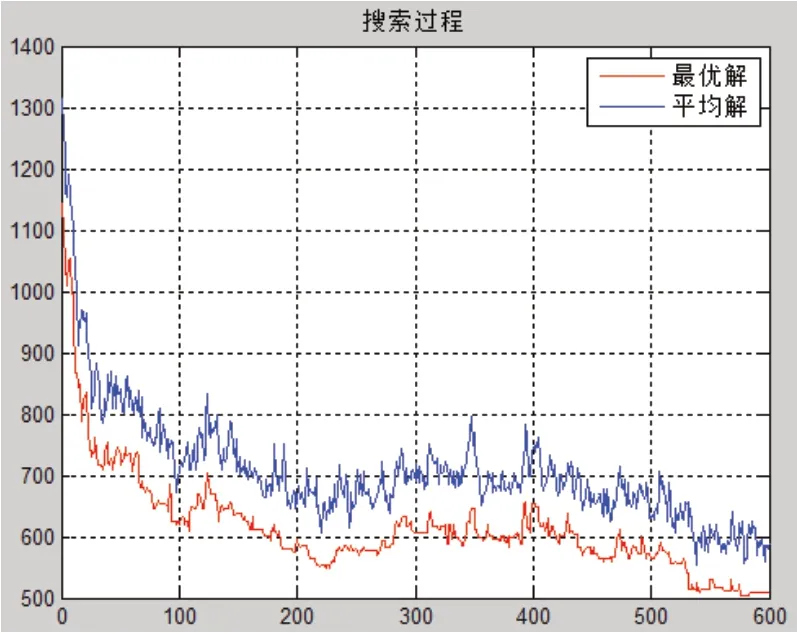
图7 GA最优解的搜索过程示意图

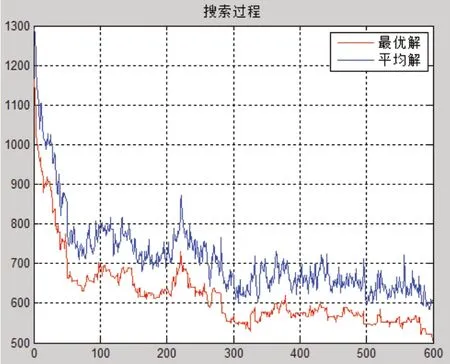
图8 GASA最优解的搜索过程示意图

5 结语

对于电商企业而言，拣货作业在仓库作业中占重要部分，合理的选择拣货路径已经成为物流企业亟待解决