400 km/h高速铁路接触网系统动态性能指标研究
鲁小兵 林宗良 杨 佳 邓云川 丁 润
(中铁二院工程集团有限责任公司, 成都 610031)
弓网关系可靠性是确保高速铁路安全运行的核心技术之一。在接触网系统设计阶段,需根据速度目标值,以特定输入下的动态性能指标为依据进行分析、设计与验证。随着京沪、成渝、鲁南、郑徐、武广等一大批350 km/h高速铁路的顺利开通,我国已经形成了350 km/h高速铁路的成套技术体系,在电气化接触网专业方面也积累了大量的工程设计经验。
速度目标值400 km/h的高速铁路代表了当前世界高速铁路技术的最高水平。但目前世界各国均未建立400 km/h接触网系统设计输入及指标体系。本文以现行标准分析、数值仿真分析、实测数据分析为基础,研究接触网波动传播速度和弓网动态性能指标等内容,初步确定400 km/h弓网评价指标,以期为工程设计与运营维护提供参考。
1 弓网系统动力学模型
本文建立适用于400 km/h弓网系统的动力学仿真模型,用于弓网系统动力学的分析与验证。
1.1 接触网模型
采用ANCF梁单元模拟接触线和承力索[1-3]、非线性索单元模拟吊弦。接触网单元类型如图1所示。
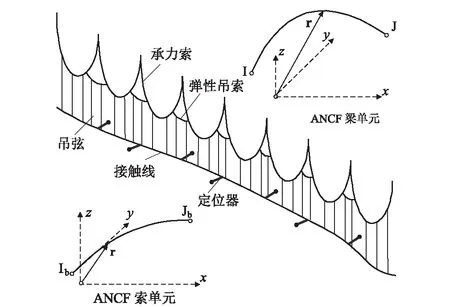
图1 接触网非线性有限元模型单元类型图
考虑一个如图1所示的ANCF梁单元,包含位移和梯度的节点自由度向量可定义为:
(1)
其中,
式中:χ——未变形结构中的局部坐标,范围为0到元素长度L0。
变形配置r中的位置矢量使用形状函数矩阵S作为内插值来表示:
r=Se
(2)
(3)
其中,
S1(ξ)=1-3ξ2+2ξ3
S2(ξ)=l0(ξ+ξ3-2ξ2)
S3(ξ)=3ξ2-2ξ3
S4(ξ)=l0(ξ3-ξ2)
通过轴向和弯曲变形贡献获得的应变可表示为:
(4)
式中:E——杨氏模量;
A——截面积;
I——线索惯性矩;
εl——纵向应变;
κ——曲率。
广义弹性力可表示为:
(5)
引入一致的质量矩阵和瑞利阻尼矩阵,接触网的运动方程可写为:
(7)
1.2 弓网耦合及模型有效性验证
受电弓模型采用国际通用的三自由度归算参数模型,弓网之间的交互作用采用罚函数方法进行描述。通过静态找形结果和动态仿真结果验证弓网模型的有效性。
(1)静态找形结果的验证
承力索吊弦点高度计算结果与其他弓网仿真软件结果的对比如表1所示[4]。从表1可以看出,本文计算结果与其他仿真软件计算结果的一致性较高。
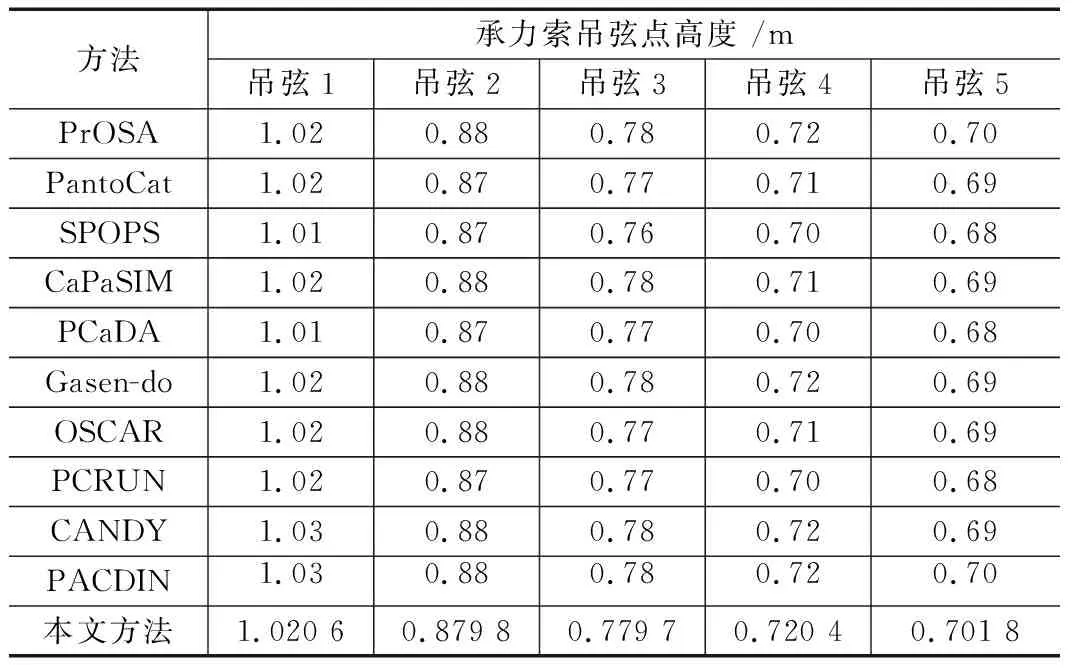
表1 承力索吊弦点高度计算结果表
(2)动态仿真结果的验证
本文仿真结果与EN 50318-2018规范[5]建议范围的对比如表2所示。从表2可以看出,本文模型仿真计算结果全部符合EN 50318-2018规范标准。

表2 仿真结果与EN 50318-2018规范对比表
2 接触网波动传播速度
2.1 设计速度
接触网设计应考虑线路最高设计速度及验收速度(设计速度的110%)。弓网受流应满足线路最高设计速度,其接触力相关统计量、离线率、定位点抬升等均须满足标准要求;验收速度下,弓网关系应满足基本受流要求;试验速度下,弓网关系应保证安全性要求,不得出现钻弓、侵限界等安全问题。
2.2 波动传播速度
接触网波动传播速度与设计速度的关系如表3所示。
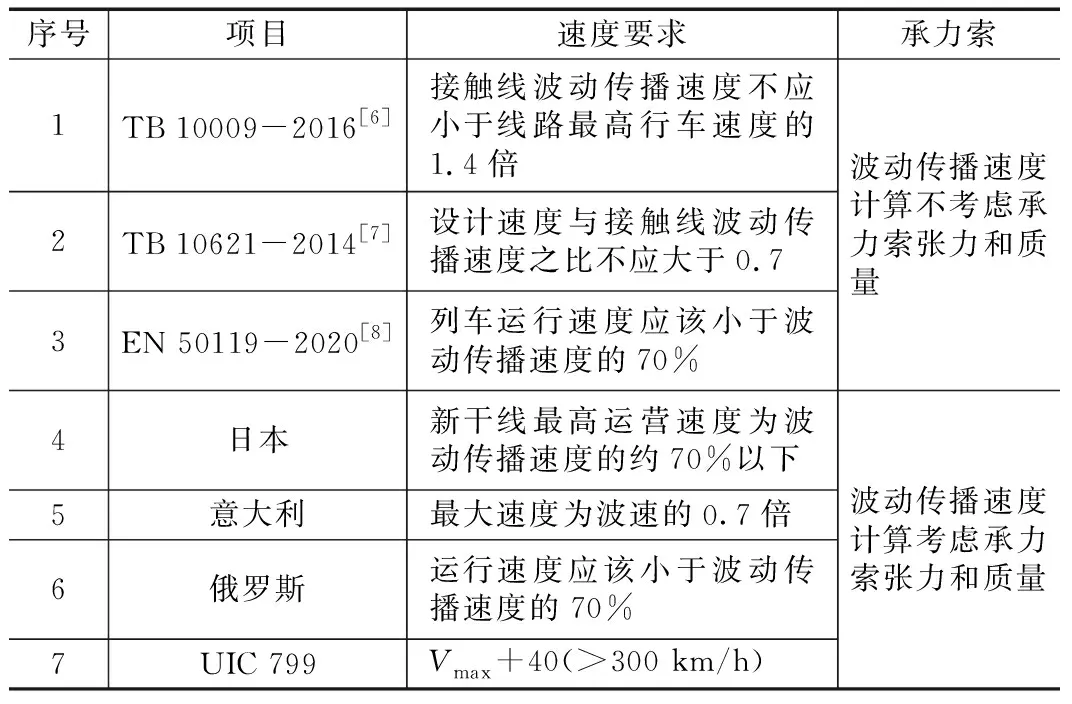
表3 接触网波动传播速度与设计速度的关系表
从表3可以看出,除UIC 799外,设计速度与接触网波动传播速度之比不应大于0.7已成为国内外铁路行业的共识。在计算波动传播速度时,国标和欧标不考虑承力索的影响,日本、意大利、俄罗斯和UIC 799考虑了承力索的影响。
2.3 计算分析
本文采用接触网初步设计参数进行仿真,分析承力索张力对弓网动态特性的影响。运行速度为 400 km/h,接触线采用150 mm2铜合金导线,承力索采用120 mm2铜合金绞线,要求波动传播速度不小于572 km/h。根据只包含接触线的波动传播速度,计算可得接触线额定工作张力不小于34 kN;根据既包含接触线又包含承力索的波动传播速度,计算可得接触线额定工作张力为 34 kN时承力索额定工作张力不小于27 kN。不失一般性,采用DSA380受电弓,接触线张力取36kN,承力索张力分别取17 kN、19 kN、21 kN、23 kN、25 kN和28 kN,仿真结果如图2~图4所示。
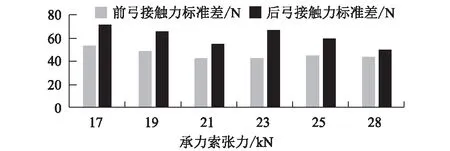
图2 不同承力索张力下接触力标准差图
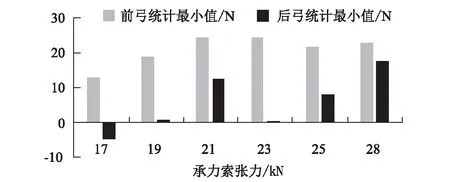
图3 不同承力索张力下接触力统计最小值图
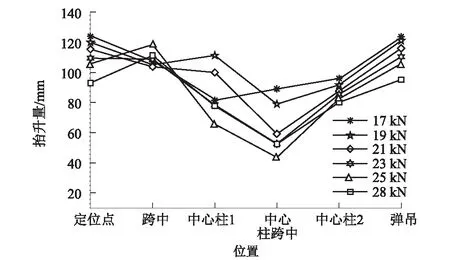
图4 不同承力索张力下不同位置处接触线抬升图
从图2~图4可以看出,承力索张力对接触力的影响在全局范围内呈非线性,但对定位点和弹吊等接触网关键位置处动态抬升的影响呈线性,即承力索张力越大,对定位点抬升的抑制效果越明显。当列车以400 km/h及以上速度运行时,弓网系统的安全显得尤为突出,需对接触线抬升重点考虑。结合现行规范和仿真结果,应将承力索张力纳入接触网波动传播速度计算(定义为复合波动传播速度),同时在接触网张力体系设计中综合考虑承力索的影响。
3 弓网动态性能指标
在接触网系统设计中,弓网关系层面的动态性能指标主要包括:最大平均接触力、最小平均接触力、最大接触力、最小接触力、接触力最大标准偏差等,其中关注重点在最大平均接触力、最小平均接触力和最大接触力三项。本节通过现有标准分析、仿真分析和实测数据对比展开研究。
3.1 现有标准分析
国内外主要标准对弓网接触力的相关规定如表4所示。

表4 国内外主要标准对弓网接触力的规定表
从表4可以看出:
(1)TB 10621-2014、TB 10009-2016(v≥250 km/h)和国外标准对最大平均接触力的规定均为 0.000 97v2+70。
(2)TB 10621-2014(v≥200 km/h)、 TB 10009-2016(v≥250 km/h)对最小平均接触力均无规定,EN 50367-2020规定最小平均接触力为 0.000 47v2+60。
(3)TB 10009-2016(v≥250 km/h)规定最大接触力为350 N,EN 50119-2020规定99.73%的接触力需在Fm±3d(d为接触力标准差)范围内,但最大接触力(v≥320 km/h)不能超过400 N。
(4)国内外规范对最小接触力的规定均为大于0。
3.2 仿真分析
本文通过弓网系统仿真,分析现有标准对最大平均接触力、最小平均接触力和最大接触力的规定在400 km/h条件下的适用性。采用400 km/h接触网系统参数初步研究成果,接触线参数为150 mm2/36 kN,承力索参数为120 mm2/28 kN,平均接触力在225 N(0.000 97v2+70)~135N(0.000 47v2+60)之间每隔10 N取值。
(1)法维莱受电弓仿真结果
法维莱受电弓时,弓网接触力统计值和接触线关键位置抬升量如图5所示。

图5 法维莱受电弓仿真结果图
(2)DSA380受电弓仿真结果
DSA380受电弓时,弓网接触力统计值和接触线关键位置抬升量如图6所示。

图6 DSA380受电弓仿真结果图
从法维莱受电弓和DSA380受电弓在最大平均接触力(0.000 97v2+70)和最小平均接触力(0.000 47v2+60)之间的仿真结果可以看出,在400 km/h接触网初步设计参数下,弓网接触力相关统计值均满足标准要求,在134 N和145 N抬升力时,DSA380受电弓锚段关节内有单点最小值为0,这可通过系统参数优化加以解决;接触力最大值基本在Fm±3d范围内,仅DSA380受电弓后弓在锚段关节个别点上的值大于Fm+3d,但仍然小于400 N。
3.3 实测数据分析
通过实测数据进一步分析弓网接触力平均值和最值的取值范围。
(1)京沪高速铁路实测数据
京沪高速铁路实测后弓接触力曲线如图7所示。
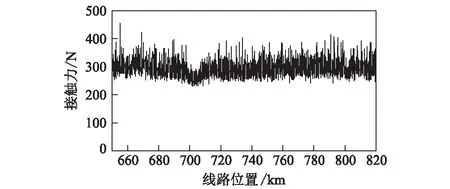
图7 京沪高铁实测后弓接触力曲线图
从图7可以看出,DSA380受电弓在380 km/h下的后弓接触力均小于400 N。需要说明的是,此接触力是京沪高速铁路先导段张力体系的实测数据,并非400 km/h接触网系统设计参数下的数据。在优选参数下,弓网接触力可得到进一步优化。
不同速度下,京沪高速铁路接触力实测数据拟合公式和现行标准接触力计算公式的结果对比如图8所示。
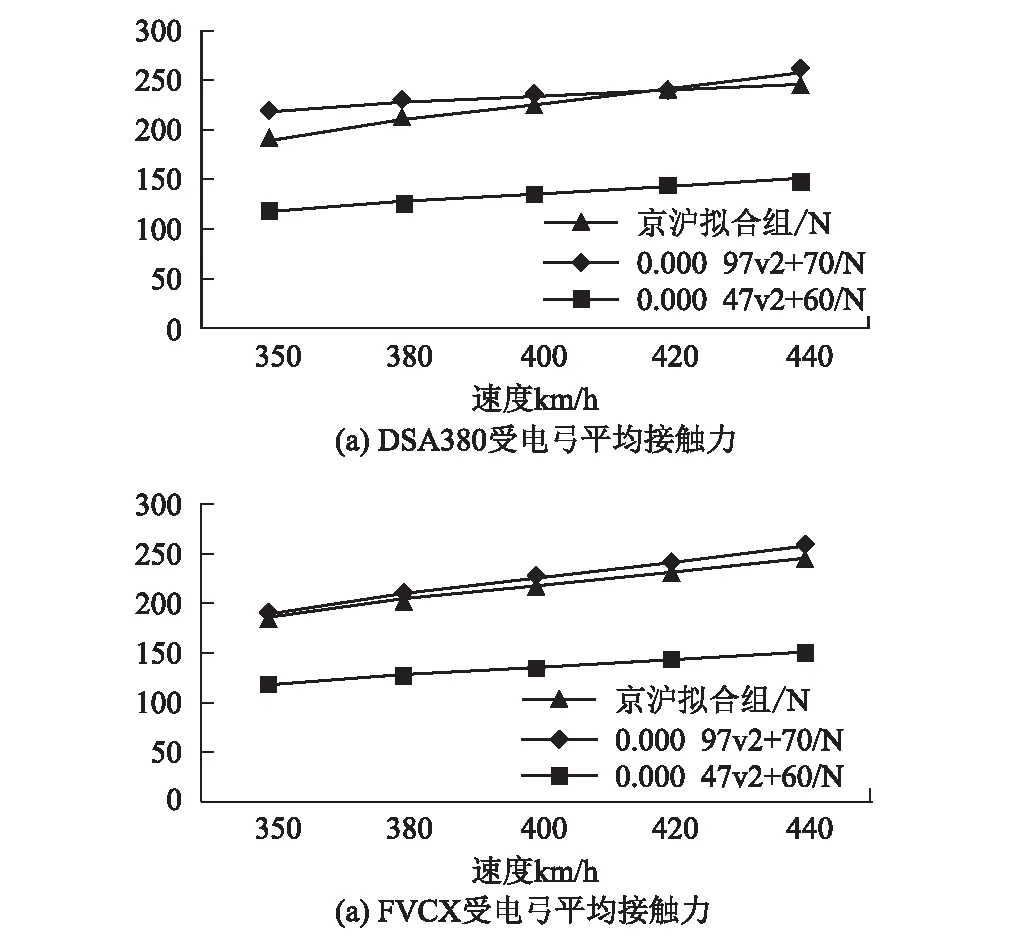
图8 实测平均接触力与标准平均接触力的比较图
从图8可以看出:随着列车速度的逐渐增大,DSA380受电弓的实测数据平均接触力逐渐靠近通用计算公式最大值,并在420 km/h时超过通用计算公式最大值。不同速度下,法维莱受电弓的实测数据拟合值均处于通用计算公式最大值和最小值之间,且较为靠近最大值。
(2)郑徐高速铁路实测数据
郑徐高速铁路实测后弓接触力曲线如图9所示。
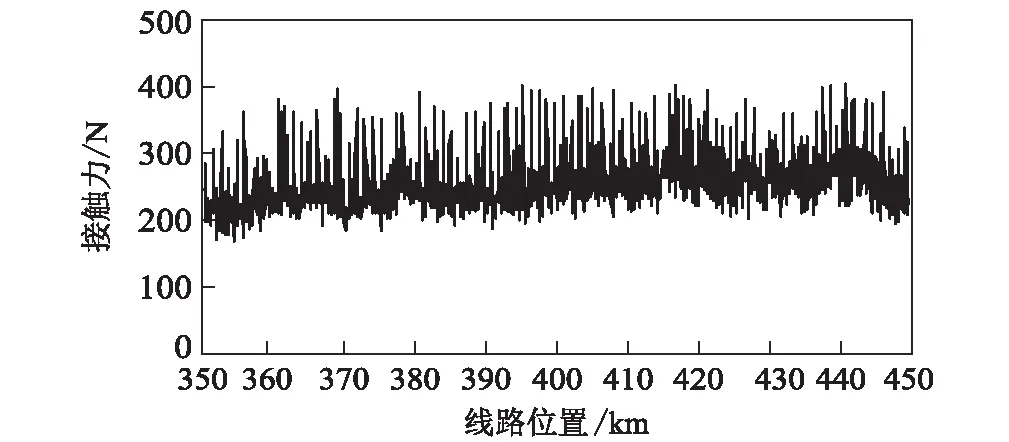
图9 郑徐高铁实测后弓接触力曲线图
综合分析京沪高速铁路和郑徐高速铁路弓网接触力的实测数据,得出以下结论:
(1)不同受电弓对弓网接触力的影响较大,且后弓接触力波动程度较前弓剧烈,此结果同仿真结果一致。
(2) 采用法维莱受电弓时,京沪高速铁路420 km/h和郑徐高速铁路400 km/h的后弓接触力均小于400 N;采用DSA380受电弓时,京沪高速铁路420 km/h和郑徐高速铁路铁400 km/h的后弓接触力有部分超出400 N。值得说明的是,该实测数据为两条线路既有参数下的测量数据,而非400 km/h接触网系统设计参数的实测结果。
(3) 在400 km/h接触网初步设计参数下,接触线(150 mm2/36 kN)、承力索(120 mm2/28 kN)和两种主流高速受电弓(DSA380和法维莱)在400 km/h下的前后弓仿真接触力均小于400 N。
(4) 接触力实测数据平均值在 0.000 97v2+70和 0.000 47v2+60之间,且接近于上限值。
基于以上分析,弓网平均接触力目标值可为 0.000 47v2+60(N)≤Fm≤0.000 97v2+70(N),弓网接触力F目标值可为0 高速铁路接触网系统设计需在确定接触网系统动态性能指标的基础上展开,本文通过仿真分析、标准对照和实测验证,对接触网波动传播速度和弓网动态性能指标进行了深入研究,结果表明:(1) 弓网平均接触力Fm目标值宜为 0.000 47v2+60(N)≤Fm≤0.000 97v2+70(N),弓网接触力F目标值宜为04 结束语

