400 km/h高速列车通过隧道气动效应数值模拟

李 艳 徐银光 李浩冉 李 田 杨邑宏

(1.中铁二院工程集团有限责任公司， 成都 610031；2. 西南交通大学牵引动力国家重点实验室， 成都 610031;3. 中国测试技术研究院， 成都 610056)

随着铁路技术的快速发展和列车运行速度的不断提高，对列车高速通过隧道时气动效应的研究愈发重要[1]。当列车进入隧道时，隧道入口处产生初始压缩波，该压缩波传递到隧道出口引发微气压波，可能发出爆炸噪音，造成环境污染[2-5]。隧道内剧变的压力波作用于车体和隧道表面影响列车运动姿态，甚至会对车体结构和隧道设施产生破坏，严重危及行车安全[6-9]。

为探究高速列车通过隧道时产生气动效应的相关机理，减弱其带来的危害程度，科研人员进行了大量的研究。占俊[10]分析了350 km/h和400 km/h速度等级列车通过隧道工况下列车表面及其附近区域的气动特性，研究了速度和编组类型对列车表面压力的影响。韩运动[11]等对列车通过隧道及隧道交会工况下的压力波特性进行实车测试，探究了运行速度和隧道长度等因素对隧道压力波的影响规律，研究结果表明：车体表面压力变化幅值与列车速度的平方成正比；车内压力幅值与列车速度的n次方成正比，n的范围为1.3～1.8，且n随隧道长度的变化而变化。刘峰[12]等采用实车试验方法对高速动车组穿越双线隧道引发的隧道壁面气动压力进行测试，分析不同位置测点在列车通过阶段和列车驶出阶段的压力峰值，研究结果表明：列车通过隧道时，壁面测点压力峰峰值随车速的增加迅速增加；列车驶出隧道后，压力峰峰值开始周期性衰减，衰减周期为2倍声速在隧道内的传播时间；在同一周期内，隧道入口处测点压力衰减率较大，出口次之，隧道中部最小。陶伟明[13]研究了洞口缓冲结构、洞身辅助坑道和隧道群开口连接明洞等对微气压波的缓解效果，发现喇叭口式和扩大常截面式缓冲结构的缓解效果要明显优于直线斜切式和等截面开口式缓冲结构；联合使用多种微气压波减缓措施可多阶段地缓解微气压波。段忠辉[14]等对高速列车进入隧道产生的压缩波波形变化及衰减规律进行了研究，研究结果表明：压缩波在隧道内向隧道出口方向传播时，基本是以平面波形式向前传播的；在隧道纵向上，平面压缩波在隧道内向前传播时，波的最大压力峰值及波形曲线压力梯度发生变化。

目前，对列车以400 km/h速度通过隧道时列车气动特性的研究较少，对此速度等级下列车表面不同位置压力变化规律和隧道出口附近不同位置微气压波变化规律的研究更是鲜有涉及。本文通过建立高速列车通过隧道的数值计算模型，对400 km/h高速列车通过隧道的相关气动效应进行探讨。

1 数值计算模型

1.1 控制方程

高速列车通过隧道时会引起隧道内部和隧道周围流场的变化，该三维、稳态可压缩流场可利用k-ε两方程湍流模型结合有限体积法求解。流体流动的控制方程可写成以下通用形式：

(1)

式中：Ω——该流场中的某一控制体；

t——时间；

ρ——理想气体的密度；

Γφ——广义扩散系数；

S——面积；

sφ——广义源项；

U——动量；

φ——通用变量。

1.2 几何模型、计算域及边界条件

为研究列车以400 km/h速度通过隧道的气动特性，以1节头车(6.8H)、6节中间车(6.3H)和1节尾车(6.8H)8车编组的CR400AF列车为研究对象，车体横截面积为11.814 m2。为简化网格划分的计算量，节约计算资源，省略掉了受电弓，并对风挡、转向架等进行了一定的简化处理，简化后的几何模型如图1所示。

图1 简化后的列车模型图

考虑到流场的充分发展和尾流的扰动，固定计算区域尺寸如下：隧道两侧计算区域长600 m，宽60 m，高40 m；隧道长650 m，断面积100 m2；列车与隧道的初始距离为100 m，列车中心线距隧道中心线2.5 m。隧道长度650 m为400 km/h速度下最不利隧道长度。使用滑移网格的方法模拟列车与其周围环境之间的相互运动，列车所在的移动计算域网格以列车运行速度相对于上述固定计算域网格滑移运动，两计算域的交界面用于两套网格之间的数据交换，流场分区示意如图2所示。

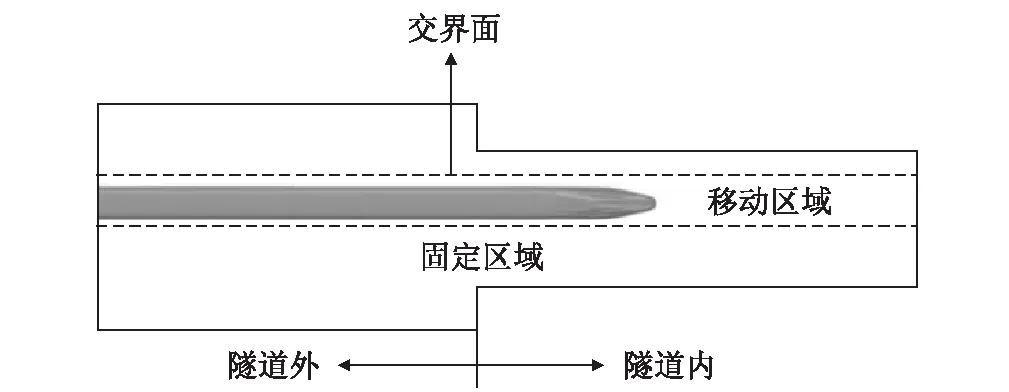
图2 流场分区示意图

将沿列车运行方向的两计算域两侧、固定计算域中隧道两侧的侧面及顶面设置为压力出口边界条件，两计算域相互滑移的面设置为交界面。计算域中的其他面均设置为无滑移壁面边界条件，采用标准壁面函数模拟，如图3所示。两个计算域均采用四面体类型非结构网格。

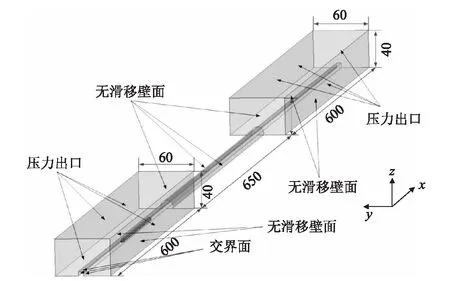
图3 计算域和边界条件示意图(m)

1.3 求解设置和测点布置

采用标准k-ε湍流模型求解列车通过隧道的流场。压力-速度耦合使用SIMPLEC算法处理，对流项、扩散项和时间项分别采用二阶迎风格式、中心差分格式和二阶隐式方法离散。时间步长为0.001 s。

为研究列车以400 km/h速度通过双线隧道的气动特性，在车体表面、隧道壁面以及隧道出口附近布置了多个压力测点，如图4所示。在列车头车靠近隧道一侧的车头流线型部分布置8个测点(HP1～HP8)，头车非流线型部分的车体两侧布置2个测点(HP9、HP10)，第1节中间车两侧布置2个测点(MP1、MP2)，第2～6节中间车布置10个测点(MP3～MP12)，尾车非流线型部分车体两侧布置2个测点(TP1、TP2)，布置情况与头车非流线型压力测点HP9、HP10相同。

图4 车体测点布置情况图

隧道壁面压力测点布置如图5所示。沿x轴正方向距隧道口20 m处和50～650 m处每隔50 m在隧道断面上布置1个压力测点，测点距离地面高度3 m。

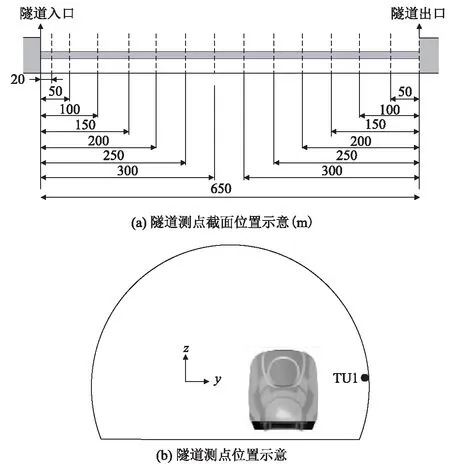
图5 隧道测点布置图

沿列车行进方向在隧道出口附近布置4组测点(MPW1～MPW5，MPW6～MPW10，MPW11～MPW15，MPW16～MPW20)，分别对应沿y轴正方向与x轴距离2.5 m、7.5 m、12.5 m、17.5 m；沿x轴正方向距隧道出口10 m、20 m、30 m、40 m、50 m，测点布置情况如图6所示。

图6 微气压波测点布置图

2 计算结果

列车通过双线隧道时，头车流线型车体靠近隧道壁面各测点的压力变化情况如图7所示。从图7可以看出：头车进入隧道后产生的第一个压缩波传播到测点时，测点压力上升，尾车进入隧道后产生的第一个膨胀波传播到测点时，测点压力下降，而后由于该压缩波和膨胀波沿隧道传播到隧道口处发生反射和转化，使得列车头部测点的压力发生剧烈变化，且靠近壁面各测点的压力变化规律相似。

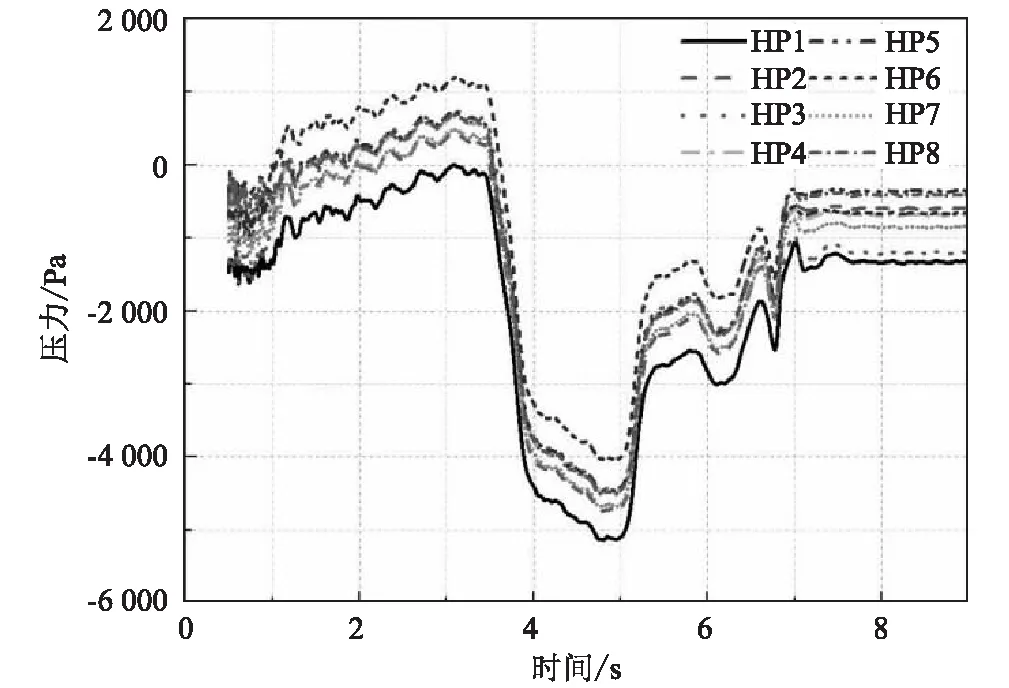
图7 头车测点压力变化规律图

通过对比隧道壁面一侧各节车厢表面压力测点的压力变化幅值可知：中间车4的压力变化幅值最大，为 5 357.1 Pa，中间车7的压力变化幅值最小，为 5 109.8 Pa，中间车4的压力变化幅值比中间车7大4.8%，各节车厢靠近隧道壁面一侧测点的压力变化幅值相近，相互之间的差异均小于5%。

靠近隧道壁面一侧各节车厢表面压力测点的负压幅值如图8所示。从图8可以看出，随着测点与头车鼻尖距离的增加，各节车厢表面的负压幅值逐渐增大，尾车的负压幅值最大，为 -4 952.6 Pa，头车的负压幅值最小，为 -4 332.46 Pa，二者相差14.3%。

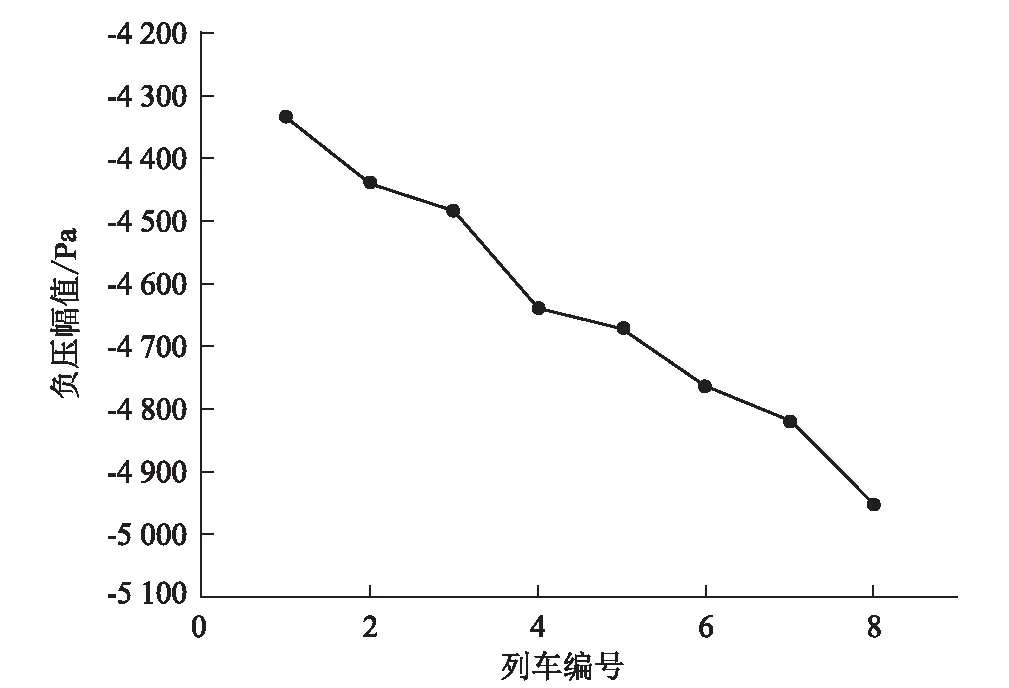
图8 各车厢车体表面测点负压幅值图

靠近列车一侧隧道壁面各测点压力变化幅值沿列车行驶方向的变化规律如图9所示。从图9可以看出：在隧道入口前20 m，隧道壁面压力变化幅值随测点距隧道口距离的增加而迅速增大，20 m后增加变缓，150～250 m处又迅速增大，在250 m处达到最大，随后缓慢减小，450 m处开始迅速减小直到500 m，500～600 m处减小较慢，600～650 m处又开始迅速减小。因此，测点位置对隧道壁面测点压力变化幅值的影响明显大于对车体表面测点的影响。单车通过长650 m、横截面积为100 m2的双线隧道时，距隧道入口250 m处测点的最大压力变化幅值为 8 083.67 Pa，隧道出口处测点的最小压力变化幅值为 1 717.34 Pa。

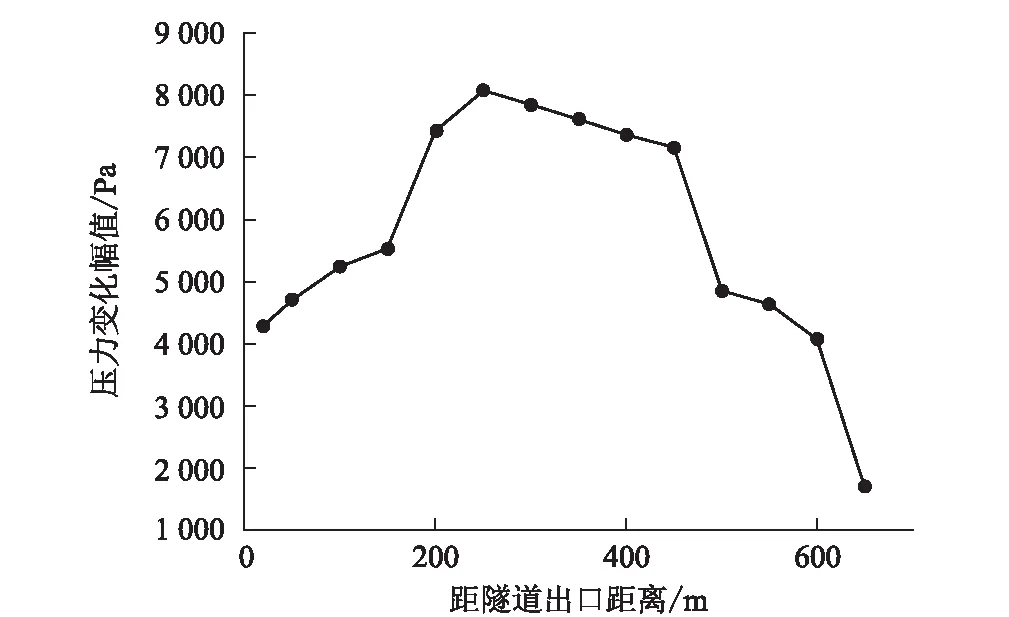
图9 隧道壁面压力变化幅值沿列车行驶方向变化规律图

垂直于隧道轴线不同横向距离各测点组微气压波幅值的变化规律如图10所示。当测点与隧道出口的纵向距离一定时，测点距隧道轴线横向距离越远，微气压波幅值越小。不同测点组微气压波具体的变化规律不尽相同。距隧道轴线最近为2.5 m的测点组(MPW1～MPW5)，其微气压波幅值随着与隧道出口距离的增加而逐渐降低，降低的幅度也随之减慢；而对于更加远离隧道轴线的其他测点组，其微气压波幅值在距离隧道出口0～40 m处逐渐降低，但在40～50 m处却开始增加，且测点组距隧道中心线的纵向距离越远，该测点组距隧道出口50 m处测点较距隧道出口40 m处测点的微气压波幅值增加得越多。

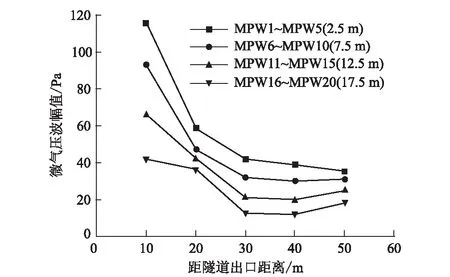
图10 垂直于隧道轴线不同横向距离测点组微气压波幅值变化规律图

3 结论

本文通过数值模拟8车编组高速列车通过650 m隧道的气动效应，得出以下主要结论：

(1)列车通过隧道时，各中间车车体不同表面测点的压力幅值差异小于5%且压力变化规律基本一致；随着测点与头车鼻尖距离的增加，车体表面的负压幅值逐渐增大，尾车负压幅值最大，头车负压幅值最小，二者相差14.3%。

(2)沿列车行驶方向，隧道壁面压力变化幅值呈现出先增加后降低的趋势，在隧道中部250 m和隧道出口位置，不同测点压力变化幅值最大相差79%。

(3)当微气压波测点与隧道出口的纵向距离一定时，其距隧道轴线横向的距离越远，微气压波幅值越小。