基于双层规划模型的高速铁路社会定价方法研究

丁昌星 许旺土 杨成和

(1.厦门大学， 福建 厦门 361000；2.中铁二院工程集团有限责任公司， 成都 610031)

近年来，随着高速铁路的飞速发展，越来越多的旅客将高速铁路作为出行交通工具的首选。相对于其他交通出行方式，高速铁路具有速度较快、安全性高的特点。在竞争激烈的交通市场中，票价是旅客选择出行方式的重要决定因素，自2016年以后，铁路票价的定价权就由政府下放到了各铁路公司，目前，我国高速铁路票价是以成本为基础，按照高速铁路时速进行分档定价的，并遵循“递远递减”的票价定制原则。

近年来，不少学者对高速铁路的定价模型进行了研究。四兵锋[1]等通过建立三层规划模型得到最优票价，保证在旅客出行费用最低的同时，客运公司能获得最大的利益；孙熙庆[2]等提出采用动态票价保证铁路收益最大化；杨宇航[3]等根据旅客对票价的敏感程度对高速铁路票价进行差别定价；卜伟[4]等提出根据乘车方向、乘车区间、订票时间等因素进行差别定价，使铁路部门收益最大化 ；徐彦将[5]旅客根据出行时间和价格敏感度进行分类，建立使高速铁路收益最大化的动态票价模型 ；杨同庆[6]利用双层规划模型求得使铁路公司经济收益最大化的铁路开行方案；吴昊[7]等提出高速铁路票价应根据弹性需求对同一通道的民航票价实行折扣。

上述制定高速铁路票价的模型基本都是从铁路公司经济收益最大化的角度来分析的，然而高速铁路作为公共交通产品，票价模型应考虑高速铁路本身的公益属性。因此，本文在高速铁路定价的双层规划模型中加入社会福利因素，在高速铁路票价定制过程考虑社会福利因素，并采用灵敏度分析法求解，得到社会福利最大化的票价。

1 考虑社会福利的双层规划模型

1.1 双层规划模型

高速铁路票价的定制可看作是一个双层决策系统，上层决策者一般为高速铁路公司，下层决策者为旅客。上层决策者对收益有要求，会对票价进行变动，下层决策者通过对当前已有交通方式优劣的判断，选择符合自己需求的交通方式。因此，双层规划模型符合高速铁路市场旅客购票选择的行为。

双层规划的一般形式为：

(U)maxF(x,y)
s.t.G(x,y)≤0
(L)minf(x,y)
s.t.g(x,y)≤0

(1)

本文中，上层规划(U)的目标是使上层决策者的社会福利最大，下层规划(L)的目标是使旅客群体在多种交通工具中选择广义出行费用最低的出行方式。

1.2 高速铁路社会定价水平双层规划模型

1.2.1 上层规划模型

根据双层规划一般的形式建立基于社会福利最大化的高速铁路票价双层规划模型。上层规划模型的目标为社会福利最大化，本文采用社会剩余来表示社会福利，社会剩余指的是消费者剩余与生产者剩余的总和。在高速铁路市场中，消费者剩余是旅客愿意支付的最高票价与实际票价的差额，生产者剩余是高速铁路公司的利润，因此上层规划模型可表示为：

maxU(p高铁j)=α×(p高铁j-c高铁j)×q高铁j(p高铁j)+β×(p高铁jmax-p高铁j)×q高铁j(p高铁j)

(2)

式中：U(p高铁j)——政府在高速铁路j坐席上获得的社会福利;

p高铁j——高速铁路j坐席的票价;

c高铁j——高速铁路j坐席运送每个旅客的平均成本;

q高铁j——乘坐高速铁路j坐席的客流量；

p高铁jmax——旅客乘坐高速铁路j坐席愿意支付的最大价格；

α——生产者剩余权重参数，α越高则社会福利中生产者的利润占比越大；

β——消费者剩余权重参数，β越高则社会福利中消费者的收益占比越大。

因此，在考虑创造最大社会福利的情况下，高速铁路社会定价水平的上层规划模型为：

maxU(p高铁j)=α×(p高铁j-c高铁j)×q高铁j(p高铁j)+

β×(p高铁jmax-p高铁j)×q高铁j(p高铁j)

s.t.p高铁j≥0

(3)

1.2.2 下层规划模型

双层规划模型的下层规划模型描述旅客选择广义出行费用最小交通方式的行为，因此，建立高速铁路票价下层规划的一般形式为：

(4)

式中：fij(x)——广义费用函数；

Q——运输通道内旅客出行需求总量；

qij——乘坐i交通工具j坐席的客流量；

I——不同交通工具的集合；

J——不同坐席的集合。

当广义费用减少时，运输通道的需求增加，但因运输通道连接城市的人口有限，运输需求不会无限制的增加，因此在下层规划中需考虑弹性需求[8]。弹性需求问题求解困难，本文通过增加冗余线路使弹性需求问题变成固定需求问题[9-10]。当运输通道内供给量与需求量相同时，下层规划模型变可转化为：

(5)

式中：Q*——各运输方式的旅客出行需求之和。

本文将旅客的广义费用函数[11]设置为：

f(qij)=a(qij)b+Vij

(6)

式中：a、b——服务属性参数；

fij——旅客选择i客运方式j坐席的广义出行费用；

qij——旅客乘坐i客运方式j坐席的客流量；

Vij——旅客乘坐客运方式i坐席j的可观测费用。

由此得到广义出行费用函数：

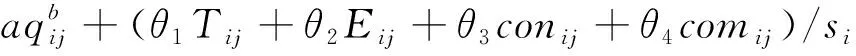
(7)

式中：Tij、Eij、Conij、Comij——旅客选择第i种客运方式坐席j的快速性、经济性、方便性、舒适性费用；

θ1、θ2、θ3、θ4——对应的权重;

Si——安全性;

I——不同运输方式的集合；

J——不同坐席的集合。

1.3 模型的求解算法

本文使用灵敏度分析法[12-13]对模型求解,具体步骤为：

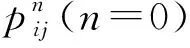
(2)将初始票价代入下层规划模型,求出客流分配量。

(3)采用灵敏度分析法得到票价和客流量的近似线性关系。

(4)将客流量与票价的近似关系代入上层规划，求出上层规划的最优票价。

(5)用新得到的最优票价反复迭代求得最优解。

2 成渝中线高速铁路二等座社会定价

2.1 定价水平

本文以成渝通道的铁路出行为例，对成渝中线高速铁路二等座的社会定价水平进行分析。当前成渝通道旅客铁路出行主要通过成渝高速铁路和成遂渝铁路，其中成渝高速铁路设计速度 350 km/h，是成渝两城间的重要客运通道,客流需求旺盛;成遂渝铁路设计速度 200 km/h，是成渝两城间的辅助客运通道。成渝中线高速铁路是成渝两城间待建高速铁路，开通初期运营速度为350 km/h，后期有望提速至 400 km/h。

假设成渝两城的乘客主要乘坐成渝中线高速铁路、成渝高速铁路和成遂渝铁路出行，采用《成渝中线高速铁路可行性研究总说明书》[14]的数据计算成渝中线高速铁路二等座的社会定价水平。设成渝中线高速铁路一等座、二等座的定价水平分别为0.99元/人公里和p2元/人公里，成渝中线高速铁路、成渝高速铁路和成遂渝铁路各坐席的可观测费用如表1所示。

表1 各高速铁路不同坐席可观测费用表(元/人公里)

本文采用孙朝苑[15]对高速铁路服务特性的研究结果，使用长途旅行服务属性权值，将各高速铁路快速性费用、舒适性费用、经济费用、方便性费用的权重分别设为 0.409 0、0.211 0、0.161 2、0.209 7,得到旅客乘坐不同高速铁路不同坐席的可观测出行费用值如表2所示。

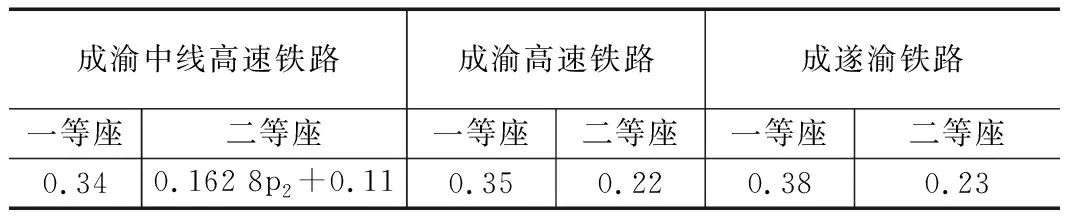
表2 各高速铁路不同坐席的可观测出行费用表(元/人公里)

设成渝两城间每日的高速铁路运输总人次为11万 人次，则需求函数d=110 000-λu，取λ=10[16]，可得虚拟客流量q0,f0(q0)=0.1q0，下层规划模型的弹性需求问题由此变成了固定需求问题。广义出行费用函数的服务属性参数a，b分别取2和0.4[17]，将表2中各高速铁路不同坐席的可观测费用乘以各高速铁路线路长度，便可建立成渝中线高速铁路二等座的社会定价双层规划模型：

maxU(P2)=[α×(p2×L-c2)×q2(p2×L)+

β×(p2max-p2×L)×q2(p2×L)]

s.t.p2≥0

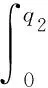
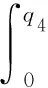
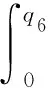
s.t.q0+q1+q2+q3+q4+q5+q6=110 000

qj>0,j=0,1,2,3,4,5,6

(8)

式中：p2——成渝中线高速铁路二等座社会定价水平；

L——成渝中线全线长度；

c2——成渝中线高速铁路二等座每运送1个乘坐全程的旅客的平均成本；

q2——成渝中线高速铁路二等座的客流量；

qj——不同高速铁路不同坐席的客流量，其中j=0,1,2,3,4,5,6分别表示虚拟路径、成渝中线高速铁路一等座、成渝中线高速铁路二等座、成渝高速铁路一等座、成渝高速铁路二等座、成遂渝铁路一等座、成遂渝铁路二等座。

考虑到当前成渝通道内各高速铁路一等座票价约为二等座票价的1.6倍，旅客心理接受的二等座最高票价不会超过一等座的票价，也不会低于二等座的票价，即1.6p2≥p2max≥p2，故取二者的均值，设旅客能接受的成渝中线高速铁路二等座最高价格p2max为票价的1.3倍，即p2max=1.3p2。《成渝中线高速铁路可行性研究总说明书》在保本微利情况下设置的票价水平为0.62元/人公里(全程181元)，取成渝中线高速铁路二等座每运输一个旅客的平均成本为0.58元/人公里(全程169.4元)。为保证上层规划模型的社会福利能同时兼顾生产者与消费者利益，取上层规划模型的ɑ为0.4，β为0.6。此时，社会福利中消费者剩余的权重略大于生产者剩余的权重，表明该权重参数的计算结果会更偏重于消费者的利益。采用灵敏度分析法对模型求解，通过matlab计算，求得成渝中线高速铁路二等座的社会定价水平为0.578元/人公里(全程168.69元)。

2.2 结果分析

作为中国第一条预留400 km/h的高速铁路，成渝中线高速铁路对成渝经济圈和中国铁路的发展都具有重大意义。因此，成渝中线高速铁路票价的定制不只要考虑高速铁路公司的收益，更要考虑适当对乘客让利，以创造更大的社会福利，更能体现高速铁路的公益性质。《成渝中线高速铁路可行性研究总说明书》拟定的成渝中线高速铁路二等座市场定价水平为0.62元/人公里(全程180元)，通过社会福利最大化双层规划票价模型计算出的成渝中线高速铁路二等座社会定价水平为0.578元/人公里(全程168.69元)，略低于市场定价水平。这是因为本文对成渝中线高速铁路二等座的定价相对更加重视消费者剩余，更符合高速铁路作为公共交通产品的定价原则，可为成渝中线高速铁路开通运营后的票价定制提供参考。

2.3 参数变动对计算结果的影响

上层规划模型中，α是生产者剩余的权重参数，β是消费者剩余的权重参数，当参数α、β变化时，成渝中线高速铁路二等座的社会定价水平也随之变化。不同α、β迭代计算的成渝中线高速铁路二等座社会定价水平如表3所示。

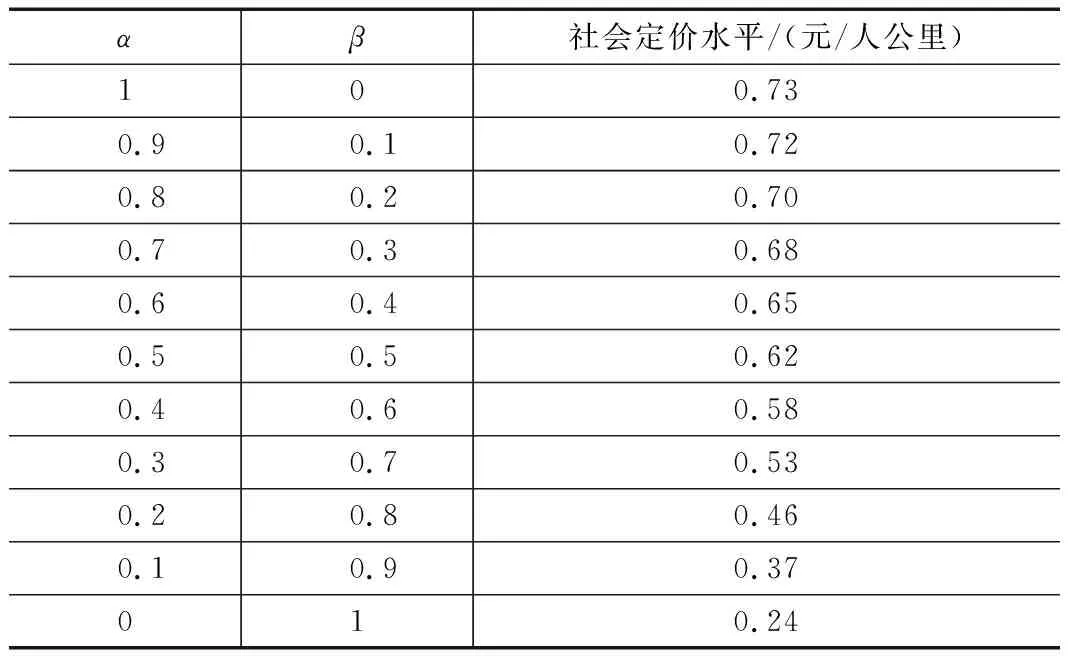
表3 参数α、β对社会定价水平的影响表

从表3可以看出，随着α的增大及β的减小，高速铁路的社会定价水平会逐渐增大，而随着α的减小及β的增大，高速铁路的社会价格会逐渐减少。这是因为α在上层规划模型中代表生产者剩余在社会剩余中的比重，β代表消费者剩余在社会剩余中的比重，本文所求的是社会福利水平最大化的票价，但从生产者也就是高速铁路公司的角度来看，票价越高，高速铁路公司获得的利润也就越高，对于旅客来说，票价越低，则旅客获得的额外净收益越大，生产者与消费者之间是存在矛盾的。当α=0.4，β=0.6时，本文求得的社会定价水平略低于设定成本，高速铁路公司会处于略微亏损的状态，表明成渝中线高速铁路二等座的定价相对更加侧重消费者利益，考虑到成渝中线高速铁路的公益属性，该定价也较为合理。若高速铁路公司想获得更高利润，则通过增大生产者剩余的权重，便可得到更高票价。同理，若高速铁路公司想创造更大的消费者剩余，则可增大消费者剩余的权重，但票价也会降低。

2.4 最高接受价格pmax变动对计算结果的影响

对旅客能接受的最高票价进行灵敏度分析，结果如图1所示。

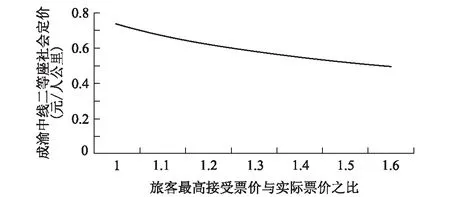
图1 旅客最高接受票价pmax对社会定价水平的影响

从图1可以看出，旅客所能接受的票价越高，社会定价水平就越低，这是因为当旅客所能接受的最高票价变高时，票价越低产生的消费者剩余就越大，从而产生的社会福利也越大。当旅客所能接受的最高票价为实际票价时，社会定价水平最高，这是因为当旅客所能接受的最高票价为实际票价时，按照消费者剩余的概念，社会福利中的消费者剩余为0，上层规划模型只考虑企业利润的最大化，当α=1且β=0时，上层规划模型同样也只考虑企业利润，因此这两种情况下的定价水平会相同。在消费者剩余权重α与生产者剩余权重β相等的情况下，当旅客能接受的最高票价小于票价的1.3倍时，票价大于成本，高速铁路公司有盈利；当旅客所能接受的票价大于等于票价的1.3倍时，票价低于成本，高速铁路公司处于亏损状态，但旅客所能得到的消费者剩余更大。

3 结束语

本文通过对制定高速铁路票价的双层规划模型进行改进，得到使社会福利最大化的双层规划定价模型，并采用模型对成渝中线高速铁路二等座的社会定价水平进行分析。结果表明，高速铁路社会定价水平会随生产者剩余与消费者剩余权重参数的变化而变化，若生产者剩余的权重变高，则高速铁路的社会定价水平也高，企业可获得更多的利润；若消费者剩余的权重变高，则高速铁路的社会定价水平会变低，消费者可享受更多的收益。高速铁路作为一种重要的公共交通工具，其票价的制定必然要考虑社会因素，遵从公益性原则，因此本文模型及分析结果可为铁路票价制定提供参考。