利用矢量的合成与分解巧解题

赵连森

（滨州实验中学，山东 滨州 256600）

矢量的合成与分解是高中物理的一个重要知识点，平行四边形定则是矢量的运算法则.高中物理课本先从位移、速度、加速度开始认识矢量，到力的合成与分解开始掌握矢量的运算方法，再到运用矢量的知识来解决运动的合成与分解问题，然后是冲量、动量以及电场强度和磁感应强度，这样逐渐把矢量的知识延展开来.可是学生在解决问题时往往不能灵活合理的使用平行四边形定则，造成解题时要么无从下手，要么繁琐冗长，总是不得其要.下面我们通过几个合理使用矢量合成与分解的实例感受一下.

例1.一匀强电场的方向平行于xoy平面，平面内a、b、c三点的位置如图1所示，三点的电势分别为10 V、17 V、26 V.下列说法正确的是

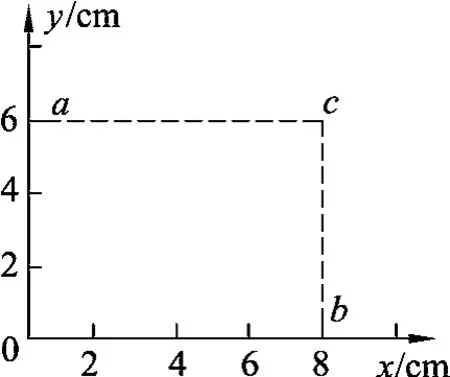
图1

（A）电场强度的大小为2.5 V／cm.

（B）坐标原点处的电势为1 V.

（C）电子在a点的电势能比在b点的低7 eV.

（D）电子从b点运动到c点，电场力做功为9 eV.

此题的正确答案是（A）、（B）、（D），关于（A）选项电场强度大小的求解，通常的解法是这样的：

因为a、b、c3点的电势分别是10 V、17 V、26 V，如图2所示，在ac连线上，确定一b点，电势为17 V，则bb′连线，即为等势线，那么垂直于bb′的连线ce，则为电场线，再依据沿着电场线方向，电势降低，则电场线方向如图2所示.

图2

因电场为匀强电场，则有

则b′点的坐标为（3.5 cm，6 cm）

依据几何关系，则

这种方法求解电场强度是最常用的方法，先确定等势面，再利用电场线与等势面垂直确定电场线的方向，最后利用电势差和沿电场线方向上的距离求解电场强度.在上面解法中，利用数学关系较多，解题过程冗长复杂.而如果依据电场强度的矢量性，先求出电场强度在x、y方向上的分矢量Ex、Ey，再合成就简单多了.

根据以上解题过程不难看出，此解法简单易懂，利用了电场强度的矢量性，先求出电场强度在x、y方向上的分矢量，再利用分矢量合成求解出合矢量.在高中物理中，除了电场强度，在解决运动的合成与分解时，把位移、速度、加速度三个矢量进行分解解题的例子也有很多.

例2.（2020年山东高考16题）单板滑雪U型池比赛是冬奥会比赛项目，其场地可以简化为如图3所示的模型：U形滑道由两个半径相同的四分之一圆柱面轨道和一个中央的平面直轨道连接而成，轨道倾角为17.2°.某次练习过程中，运动员以vM=10 m／s的速度从轨道边缘上的M点沿轨道的竖直切面ABCD滑出轨道，速度方向与轨道边缘线AD的夹角α=72.8°，腾空后沿轨道边缘的N点进入轨道.图4为腾空过程左视图.该运动员可视为质点，不计空气阻力，取重力加速度的大小g=10 m／s2，sin72.8°=0.96，cos72.8°=0.30.求：

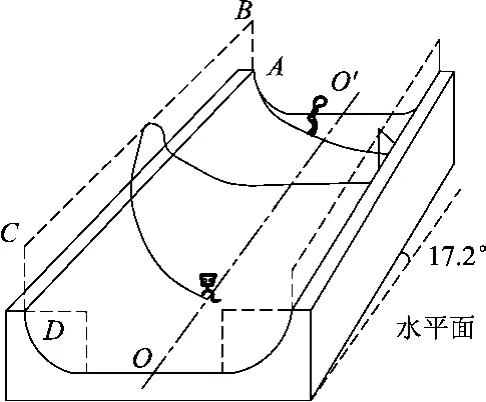
图3

图4

（1）运动员腾空过程中离开AD距离的最大值d；

（2）M、N之间的距离L.

此题用运动的合成与分解解题是最快捷的，把速度和加速度分别沿垂直于AD和平行于AD方向进行分解，然后沿各自方向计算位移即可.解法如下.

对于此题中这种较复杂的曲线运动，要解题还是要根据运动的矢量性，把复杂的曲线运动分解成两个直线运动，再利用它们的位移、速度、加速度关系进行求解.

上例的特点是可以清晰的看出物体做曲线运动的轨迹，我们把曲线运动分解成两个直线运动，再根据各分运动的性质来求解即可.还有的问题是没有给出物体的运动轨迹，仅是已知分运动的运动情况，让我们根据位移、速度、加速度的矢量性来解决问题.

例3.（2013年全国Ⅰ卷24题）如图5所示，水平桌面上有两个玩具车A和B，两者用一轻质细橡皮筋相连，在橡皮筋上有一红色标记R.在初始时橡皮筋处于拉直状态，A、B和K分别位于直角坐标系中的（0，2L）、（0，-L）和（0，0）点.已知A从静止开始沿y轴正向做加速度大小为a的匀加速运动.B平行于x轴朝x轴正向匀速运动.在两车此后运动的过程中，标记K在某时刻通过点（L，L）.假定橡皮筋的伸长是均匀的，求B运动速度的大小.

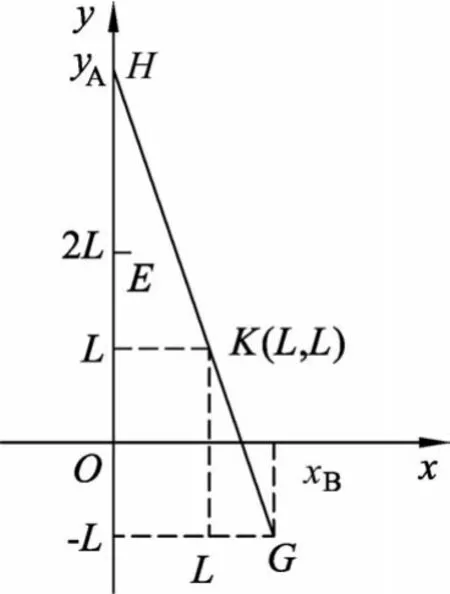
图5

此题没有给出标记K具体的运动轨迹，但根据运动关联性，能够知道其在x、y方向上的分运动情况：x方向上匀速直线运动，y方向上匀加速直线运动.知道了分运动情况，沿x、y分方向处理就可以了.

通过以上几例可以看出，根据矢量运算的特点，利用好矢量的分解与合成解题，很多情况是简单易懂的.回顾高中学习的物理量，最常用的矢量主要是位移、速度（动量）、加速度、力（冲量）、电场强度和磁感应强度，在学习过程中多注意这几个矢量的合成与分解就可以了.