基于随机生成矩阵的加密算法

邢伟 陈大文

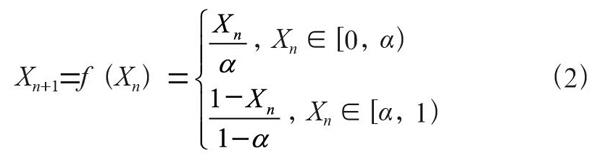
DOI：10.19850/j.cnki.2096-4706.2021.08.052

摘  要：边缘计算技术能够有效地弥补传统云计算的不足，然而也带来了非常大的安全隐患。面对这一问题，相关学者从数据完整性、数据机密性以及隐私保护三个方面展开研究。文章针对原有研究在对于原始数据损害较大、相关算法框架较为复杂的基础上，引入一种基于混沌函数的理念来随机生成可逆矩阵，对原始数据进行加密，再使用逆矩阵进行解密，能够有效地保证数据原始的特征，提高安全性。文章最后通过实验证明该方案具有一定的可行性。

关键词：边缘计算;混沌函数;加密

中图分类号：TP309      文献标识码：A    文章编号：2096-4706（2021）08-0183-03

Encryption Algorithm Based on Randomly Generated Matrix

XING Wei，CHEN Dawen

（Jiangsu Golden Shield Detection Technology Co.，Ltd.，Nanjing  210042，China）

Abstract：Edge computing technology can effectively make up for the shortcomings of traditional cloud computing，but it also brings great security risks. Faced with this problem，relevant scholars have started their research from three aspects：data integrity，data confidentiality and privacy protection. In view of the original research，on the basis of great damage to the original data and complex algorithm framework，this paper introduces a idea based on chaotic function to randomly generate the reversible matrix，encrypt the original data，and then use the inverse matrix to decrypt，which can effectively guarantee the original characteristics of the data and improve the security. Finally，experiments show that the scheme has a certain feasibility.

Keywords：edge computing;chaotic function;encryption

0  引  言

隨着5G时代的到来，人们对于网络的需求越来越强烈^[1-3]。一方面，用户群的急速扩大导致数据量的爆炸式增多，原有的技术对于数据的计算、存储等功能需求已经不堪重负;另一方面，高时延、低效率的响应已不能满足用户实时获取信息的迫切需求。因此，边缘计算进入了人们的视线。

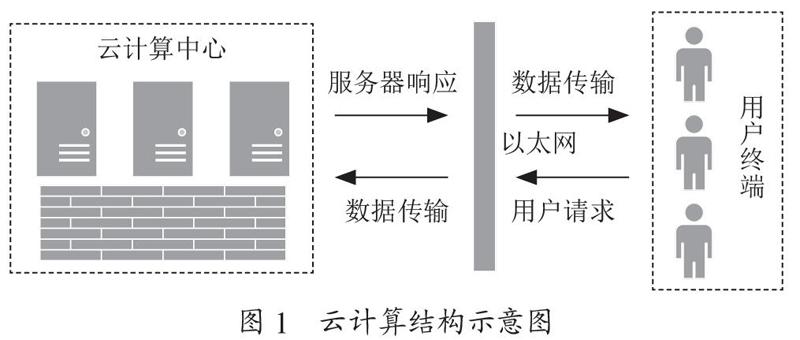
原先，云计算技术需要将用户的所有请求、所有的数据计算等都汇聚到云计算中心（如图1所示），在此过程中数据仅仅只会经过用户终端和云计算中心两个端点，所以只要在云计算中心实施重点的安全防护措施就可以有效地提高数据的安全性，降低数据泄露风险。而对于云计算的安全研究以及相关技术已经相对成熟^[4，5]，所以云计算中心往往有着较强的安全防护能力，黑客不易对其进行大规模攻击，数据也不会大规模泄露。边缘节点不像中心云那样有着非常完备的数据安全体系，所以，在这个背景下，如何提高数据的安全性成为相关学者的研究热点。

边缘计算的数据安全性主要分为数据完整性、数据机密性以及隐私保护三个方面，其对应的解决方案分别是数字签名技术、数据加密技术以及隐私保护技术。数字签名技术（又称公钥数字签名）是只有信息的发送者才能产生的别人无法伪造的一段数字串，这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。数据加密技术是指在数据传输过程中对原始数据进行加密，进而保证数据的安全性。隐私保护技术（如生物识别技术^[6]、多方安全计算技术^[7，8]）可以有效地保护数据隐私等。对于数据加密技术，Paillier^[9]提出了一种基于复合度剩余类的公钥密码体制，并且引入了一种新的陷阱门（trapdoor）机制;陈智罡^[10]等人对全同态加密进行了相关研究，并从噪声、参数记忆性能和安全性等方面对每个加密方案进行了探讨;Kim^[11]等人提出了一种基于身份的广播加密技术，能够很好地减少资源开销。

然而这些加密算法与加密方案在边缘计算框架中过于复杂，用户终端设备的计算能力无法完全满足解密时所需的资源需求，进而造成数据解密失败、无法获得返回的数据信息等情况的发生。构造轻量化且安全性高的加密算法是比较重要且具有一定难度的研究话题，因此，相关学者将目光转向了数据扰动技术。数据扰动技术主要是在不改变或者轻微改变数据特征并且不影响有序数据计算的基础上向数据添加噪声，从而达到数据隐私保护的目的。数据扰动技术主要是进行数据扭曲与交换，以及基于概率分布的扰动进行展开，其主要的扰动机制通常包括微聚集、添加噪声、加密以及多方计算等。数据扰动算法通过对用户端的原始数据进行随机扰动，对数据进行模糊化，隐藏了数据中的敏感信息。这个方法的好处是不用考虑攻击的类型与方式就可以很好的保证数据的隐私性，国内外的专家学者对此也有了广泛的研究。在这方面，有如运用离散小波变换实现数据扰动的研究^[12]，也有黄茂峰^[13]等人提出的一种面向聚类的对数螺线数据扰动方法，Mukherjees等人^[14]提出了一种基于傅里叶变换的数据扰动方法也可以很好地提高数据的安全性。采用加密的方法对数据实施扰动有一个基本的要求，就是不能修改数据分布，因为如果改变了数据的分布，那么数据就没法进一步地分析了，失去了数据的使用价值。但是现在的大部分加密算法会改变数据的分布特征，如非对称加密算法以及部分对称加密算法。因此，本文提出使用一种基于矩阵作为密钥的数据同分布加密算法。因为矩阵运算并不会改变输入数据的分布特征，从而实现数据扰动同时保持数据分布的目标。

1  基于随机生成矩阵的加密算法

1.1  矩阵加密算法概述

针对矩阵加密算法，目前也有了相关的研究，彭一哲^[15]提出了一种单向HASH函数下的密钥矩阵加密方法，通过混沌理论来加密构造单向HASH函数，所谓单向HASH函数即是单向散列函数，换言之，就是把任意长的输入消息串变化为固定长度的输出串，在此基础上无法从输出串中得到输入串的一种函数，然而，连续系统的离散化和算法相对复杂，计算量大，这是一个亟须解决的问题。徐丽新^[16]等人提出了一种基于整数矩阵乘法的图像加密算法，通过可逆矩阵的变换达到了对于图像数据的隐私保护，而且，该研究提出的整数环可逆矩阵在安全性上表现非常出色，因为整数环的个数是无限的，所以密钥的空间非常庞大，很难通过穷举法等进行破译，有效地保护了数据隐私。

1.2  构造加解密可逆矩阵方案

混沌系统是指在一个确定性系统中，存在着貌似随机的不规则运动，其行为表现为不确定性、不可重复、不可预测，这就是混沌现象。混沌映射主要有logistic映射和和tent映射。

1.2.1  logistic映射

logistic映射的主要映射形式如式（1）：

X_n+1=X_n·μ（1-X_n）                        （1）

其中，μ∈（0，4]，X_n∈（0，1），n=1，2，3，…。

1.2.2  Tent帐篷映射

帐篷映射（tent map），在数学中是指一种分段的线性映射，因其函数图像类似帐篷而得名。除此之外，它还是一个二维混沌映射，其广泛运用在混沌加密系统中（如图像加密），并且在混沌扩频码的产生、混沌加密系统构造和混沌优选算法的实现中也经常被使用。帐篷映射的定义为：

由于本文使用矩阵作为加解密的密钥，即矩阵A作为加密密钥，那么其逆矩阵就作为解密密钥，因此通过混沌函数生成加密密钥矩阵的关键在于利用混沌函数生成的随机数构造可逆矩阵，在本文实验中选用Tent帐篷映射混沌函数来生成加密矩阵。

可逆矩阵生成算法为：

（1）先确定加密密钥矩阵的维度为N×N。

（2）生成N×N的单位对角矩阵。

（3）预定一个参数作为生成加密密钥矩阵的迭代次数。

（4）执行循环：

如果：

已经达到预定的迭代次数停止循环。

否则：

1）执行混沌函数生成四个随机数，假设混沌函数生成随机数为浮点实数。

2）确定矩阵变换方式，第一随机数与第二个随机做比较，如果大于则当前执行矩阵行变换，否则当前执行矩阵列变换。

3）第一随机数与第二个随机数取绝对值并变换取整，取整结果为0到N-1，作为本次矩阵初等变换的参与行或列，其中值大的为主行，值小的为次行。

4）将次行乘以第四个随机数加到主行，并判断加后主行的各分量是否有溢出，如果有则放弃本次变换，返回循环，重新开始一次迭代。如果没有，完成一次初等变换。

（5）完成循环的矩阵即为可逆矩阵，直接对该矩阵求逆，获得对应的解密矩阵。

1.3  基于随机生成矩阵的加解密算法实现

经过1.2小节中的操作之后生成了加密与解密的随机生成矩阵，进而实现基于随机生成矩阵的加解密算法则采用以下步骤：

（1）对需要加密的数据按加密密钥矩阵的维度进行排列与组织，切成（N×N）数据块。

（2）设数据长度为L，则可能会有L%（N×N）个剩余数据，对于剩余数据需要在最后一个数据块中进行填充，填充数为N×N-L%（N×N），可再利用混沌函数生成数据进行填充。

（3）逐块对切分并填充的数据块进行加密，再后将1，e₂，e₃，…，e_n>作为最终完成的加密结果发送给接收方，其中L为原始数据长度，ei为加密完成的数据块。

（4）接收方在接收到密文后，利用解密矩阵逐块对加密数据块进行解密，再根据接收的数据原长，即可恢复原始数据。

2  实验

设1.2节中生成的混沌可逆矩阵为B，其逆矩阵为B^-1，设原始数据矩阵为A。首先使用矩阵B对原始数据矩阵A进行加密。加密过程如图3（a）所示。经过矩陣B加密后生成密文矩阵C，解密是加密的逆过程，如图3（b）所示，用矩阵B-1对矩阵C进行右乘，最终得到解密后的数据矩阵A。

本文使用了18岁至44岁的5 000个男性身高作为本次实验数据集（Statistics Online Computational Resource，SOCR），原始数据分布符合正态分布特征，图4（a）为原始的数据分布，均值μ=169.71，σ²=3.10。经过上述步骤操作，通过可逆矩阵解密后的数据分布为图4（b），与原始分布基本相似，且μ=169.83，σ²=3.10。从而可以认为，经过本文所提出的方案能够在不改变数据原始特征的基础上提高数据的安全性，实现了又能抵抗数据泄露，又能提高后期计算精度的预期目标。

3  结  论

在针对原有数据加密方案计算效率低下、加密效果不理想的问题下，本文提出了一种基于混沌函数的随机生成可逆矩阵用来作为加密和解密密钥，提高数据安全性的同时能够不改变原始数据的分布特征，保证数据的原始性。本文提出的方案虽然计算方式简单，生成混沌可逆矩阵的过程也不复杂，但是，对于数据量较大的数据，进行矩阵运算的计算量还是较大，也是我们今后研究的重点。

参考文献：

[1] MONTRESOR A. Reflecting on the Past，Preparing for the Future：From Peer-to-Peer to Edge-Centric Computing [C]//IEEE International Conference on Distributed Computing Systems.IEEE，2016.

[2] MAO Y，YOU C，ZHANG J，et al. A Survey on Mobile Edge Computing：The Communication Perspective [J].IEEE Communications Surveys and Tutorials，2017，19（4）：2322-2358.

[3] 施巍松，孫辉，曹杰，等.边缘计算：万物互联时代新型计算模型 [J].计算机研究与发展，2017，54（5）：907-924.

[4] 冯登国，张敏，张妍，等.云计算安全研究 [J].软件学报，2011，22（1）：71-83.

[5] 王于丁，杨家海，徐聪，等.云计算访问控制技术研究综述 [J].软件学报，2015，26（5）：1129-1150.

[6] 郑方，艾斯卡尔·肉孜，王仁宇，等.生物特征识别技术综述 [J].信息安全研究，2016，2（1）：12-26.

[7] 李顺东，王道顺.基于同态加密的高效多方保密计算 [J].电子学报，2013，41（4）：798-803.

[8] 李强，颜浩，陈克非.安全多方计算协议的研究与应用 [J].计算机科学，2003（8）：52-55.

[9] PAILLIER P. Public-key cryptosystems based on composite degree residuosity classes [J].EUROCRYPT99：Proceedings of the 17th international conference on Theory and application of cryptographic techniques，1999（5）：223-238.

[10] 陈智罡，王箭，宋新霞.全同态加密研究 [J].计算机应用研究，2014，31（6）：1624-1631.

[11] KIM J，CAMTEPES ，SUSILO W ，et al. Identity-Based Broadcast Encryption with Outsourced Partial Decryption for Hybrid Security Models in Edge Computing [J].s.n.，2019：55-66.

[12] 剧高峰，罗安.离散小波变换用于电能质量扰动数据实时压缩 [J].电力系统自动化，2002（19）：61-63.

[13] 黄茂峰，倪巍伟，王佳俊，等.一种面向聚类的对数螺线数据扰动方法 [J].计算机学报，2012，35（11）：2275-2282.

[14] MUKHERJEE S，CHEN Z，GANGOPADHYAY A. A privacy-preserving technique for Euclidean distance-based mining algorithms using Fourier-related transforms [J].The VLDB Journal，2006，15（4）：293-315.

[15] 彭一哲.混沌单向Hash函数的构造研究 [D].长沙：长沙理工大学，2013.

[16] 徐丽新，吴明珠.基于整数矩阵乘法的图像加密算法 [J].电子制作，2019，373（9）：45-47.

作者简介：邢伟（1986.10—），男，汉族，江苏南京人，中级工程师，高级测评师，CISP，CIIPT，本科，研究方向：网络应用与安全;陈大文（1989.11—），男，汉族，江苏南京人，中级工程师，高级测评师，CISP，CIIPT，本科，研究方向：网络应用与安全。

收稿日期：2021-02-10