ADS-B地面站的目标定位技术研究

浙江空管分局 王旭刚

随着ADS-B系统在空管监视工作中的重要性越来越高，我们对其监视目标的稳定性与准确性提出了更高的要求，目前系统存在的缺陷、问题也亟待解决。本文以当前ADS-B运行中出现的目标位置偏差问题为出发点，通过对ADS-B系统与多点定位系统（MLAT）的定位原理进行分析，提出了一种基于ADS-B的多基站定位方法，并通过在一定GDOP前提下，对涉及的算法进行仿真，说明了估值均方根误差的大小。该方法得到的目标位置独立于GNSS设备提供的位置信息，为提高ADS-B监视系统的位置准确性提供了一种辅助手段。

广播式自动相关监视系统（ADS-B）作为一种新型航空监视技术，因其高精度、高刷新率、低成本及便捷部署等优势，近几年在我国大部分地区均建设了此类设备。尤其在雷达覆盖不足的地区，ADS-B作为主要监视手段使用，对我国航空安全起到了重要作用。但是随着运行的不断深入，ADS-B系统存在的一些突出问题也逐步显现，其中ADS-B监测到的航空器位置与真实目标存在偏差是常见的问题之一。本文针对ADS-B位置偏移问题，通过提出一种基于ADS-B的多站点定位方法解决目标位置偏移问题，并通过MATLAB软件对其定位算法的均方根误差（RMSE）仿真对比，希望能对逐步完善ADS-B设备起到抛转引玉的作用。

1 基于ADS-B多基站定位原理

ADS-B地面站设备是通过地面接收技术完成对指定监视区域内目标飞机实时探测并确定其位置。ADS-B机载设备以一定的速率对外广播指定的信息。地面站设备将信息格式按照EUROCONTROLAsterixCAT021标准要求解析，其中必须包含的数据项包括I021/073（位置信息接收时间）、I021/130（基于WGS-84坐标的位置信息）、I021/080（目标地址）等共15项。非必选项包括I021/070（3/A码）等27项，同样包含着许多重要的信息，对ADS-B应用有着重要的作用。其中机载ADS-B设备广播信息中的位置信息来源为直接取自机载GNSS设备的卫星定位信息。

目前国内的多点定位系统的定位原理大都是通过基于目标信号达到时间差TDOA（Time Difference of Arrival）来定位。TDOA的原理是通过多个地面基站接收到发射源的时间差来定位。进行二维定位时，最少需要三个地面接收站；进行三维定位时，最少需要四个地面接收站。图1简要图示了三维TDOA定位的定位原理。

图1 三维定位示意图

以三维定位为例，目前存在N个ADS-B地面站，第i个地面站的位置矩阵为si=[xi yi zi]T，i=1，2，3……，N，目标位置为d=[x y z]T。可知，目标d到达第i个地面站的距离为||d-si||。本文以s1作为主参考ADS-B接收站，则其位置矩阵为s1=[x1y1z1]T。根据优化算法得到则TDOA的匹配方程如下：

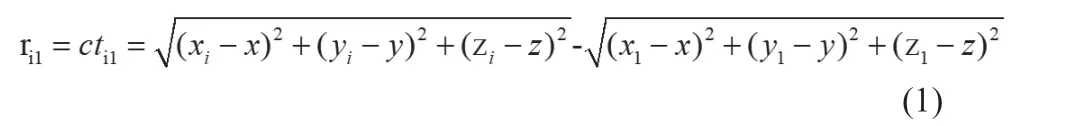
选择4个ADS-B地面基站联立方程组，可得：

c是信号传播速度，ti1是目标信号到达ADS-B地面接收站si与到达地面主接收站s1的时间差，ri1是目标信号到达接收站si与到达接收站s1的距离差。由于c是电磁传播速度常数，根据公式R=ct我们认为此时的时间t与距离R成正比。因此对公式(2)简化后，得到如下矩阵公式(3)。

其中：

可知目标位置矩阵X如下：

式中，矩阵A表示地面站之间三维距离坐标差，矩阵X表示目标的三维坐标，F为参数多项式矩阵，x34表示3号地面站与4号地面的x轴距离差，以此类推。xi表示i号地面站的x坐标值，以此类推。

由于ADS-B地面站对航空器的定位依赖于机载GNSS设备广播的位置信息，当机载GNSS位置信息出现偏差时，地面基站探测到的位置也同样偏差。本文以多点定位系统原理出发，利用ADS-B报文信息中的时间信息，将多个ADS-B地面基站收到的到达时间差进行TDOA分析，实现三维定位得到目标位置信息，而不依赖于GNSS的位置信息。ADS-B地面基站送出的Asterix CAT021报文中，包含有该地面基站最近一次位置信息接收时间，分别为数据项I021/073（精度1/128s）和数据项I021/074（精度2-30s）。各个地面站以CAT021格式，将目标数据报文汇总至ADS-B数据中心，数据中心根据上述TDOA定位原理，根据所接入的地面站收到目标信号到达时间进行计算，得到目标距离各个地面站的距离位置差，根据矩阵公式(4)及相关算法，计算得到目标实际距离，以达到多地面基站定位的目的。

2 定位算法误差仿真

在分析多点定位系统定位效果时，必须提到几何精度因子（GDOP），它是一种描述纯粹因接收站几何位置因素对定位精度的影响。它表征多点定位系统测量误差造成的监视点与空间接收站的距离矢量放大因子。视点到接收站的单位矢量所勾勒的形体体积与GDOP成反比。因此，在讨论算法误差的时，应当以特定的GDOP因子为前提。

本文设定在正方形分布下的GDOP前提下，讨论多点定位算法中Chan算法与Taylor算法，二者为TDOA定位的经典算法。图2为在引入噪声因素的前提下，利用MATLAB分析软件，以均方根误差（RMSE）为指标，对基于ADS-B的多地面基站定位方法中使用这两种算法的性能进行对比，得到两种算法的RMSE曲线对比图，如图2所示。

图2 CHAN算法与Taylor算法的RMSE曲线对比图

从图2中可以看出，在测量噪声较小时，Chan算法与Taylor算法的RMSE相似，表征两种算法此时性能差距不大；在测量噪声加大后，Taylor算法的性能优势逐渐凸显。Taylor算法的前提是需要目标位置的初始估计值，算法的主要思想是通过不断迭代来修正待定位标签位置的估计值，最后逐渐逼近目标真实的位置坐标，适用范围广，但是如果初值选择不合适，有可能导致算法不收敛。而Chan算法计算速度快，但是存在精度不高的缺点。因此目前大都采用Chan-Taylor混合加权算法，将Chan算法计算出来的估计值作为Taylor级数展开法的迭代初始值带入，之后合理设置Chan算法和Taylor级数展开法的加权系数来提高精度。

结论：近年ADS-B技术在我国得到了广泛应用，在二次雷达覆盖不足的区域，起到了重要作用，在东部地区也作为空管自动化系统的一个重要数据源接入。同时也普遍出现了因为ADS-B信号源目标位置偏移导致的隐患和故障。本文讨论的定位方法基于ADS-B CAT021报文数据中的地面站接收信号的时间数据，采用多点定位原理与算法，实现三维目标定位。该方法所得到的位置信息与机载GNSS下发的位置信息不相关，可以作为ADS-B目标定位的辅助手段，以提高其定位目标的可靠性、精度。同时本文将定位中用到的Chan算法和Taylor算法性能（RMSE指标）进行了MATLAB仿真、对比。考虑到GDOP因素，如果需利用本文提出的方法提高ADS-B定位的可靠性，在今后建站选址中，需要将全网ADS-B地面站进行总体考虑，综合计算GDOP，以达到理想效果。