基于DXF的复杂工件标定及相机参数优化

于跃华，王好臣，赵锦泽，丛志文，高茂源，李家鹏

(山东理工大学机械工程学院，山东 淄博 255000)

0 引言

目前具有视觉识别的机械臂末端定位技术早已成为机器视觉研究的热点问题，基于视觉识别伺服的机器人逐渐被应用到各种行业中，比如焊接机器人、工件分拣机器人等，极大地提高了我国工业的生产效率与自动化程度[1-3]。在实现对工业机器人视觉引导的过程中，有效提高工件与相机内参的标定精度成为了视觉伺服在工业应用中亟待解决的关键问题[4]。

本文在工件标定时对易使用CAD建模的工件进行DXF文件提取，将CAD工作单元与实际工作单元中的工件进行调整与坐标转换，为工件标定提供了图元坐标信息，有效地减少了人工示教。针对相机标定提出了一种基于自适应权重粒子群算法的参数优化方法，该方法在传统粒子群算法的基础上建立了自适应权重函数，提高了全局搜索能力，避免了传统算法优化时易陷入局部最优的问题，有效提高了标定精度。

1 复杂工件标定

标定复杂零件时，针对不同零件需采用适合的标定方法，常见的复杂工件一般为具有圆形基准面或相交平面的工件，极少出现更复杂的三维图形，因此只针对存在圆基准面和正交平面的工件进行标定研究。

1.1 圆形基准工件四点标定法

四点标定法(图1)用于具有圆形定位基准的工件，优点为只需要找出基准圆上任意不同三点和工件上的一个其他基准点即可。

图1 圆弧四点标定法

基准圆的尺寸及圆心位置由其上任意三点确定，圆的位置信息则通过另一明显基准点来确定，调整工件时先使两基准圆重合，再将工件上的特征点对应，最后绕基准圆过圆心的法向轴线旋转一定角度即可[9]。

设b1(Xb1，Yb1，Zb1)，b2(Xb2，Yb2，Zb2)，b3(Xb3，Yb3，Zb3)三点分别为CAD环境中基准圆上任意三点，b4(Xb4，Yb4，Zb4)为工件上任意特征点，则该基准圆的平面法矢量和圆心b0(Xb0，Yb0，Zb0)可以确定，点b1，b2，b3确定的圆平面方程可由下式表示：

Ab1(X-Xb1)+Bb1(Y-Yb1)+Cb1(Z-Zb1)=0

(1)

式中：

Ab1=(Zb3-Zb1)(Yb2-Yb1)-
(Zb2-Zb1)(Yb3-Yb1)
Bb1=(Zb2-Zb1)(Xb3-Xb1)-
(Zb3-Zb1)(Xb2-Xb1)
Cb1=(Xb2-Xb1)(Yb3-Yb1)-
(Xb3-Xb1)(Yb2-Yb1)

定义该平面的法矢量为CAD单元中工件坐标系的Zb轴矢量，可表示为：

Zb=αbzi+βbzj+γbzk

(2)

其中：

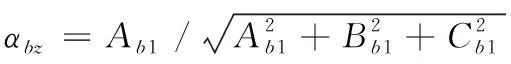
圆心b0的位置可由圆的方程得出：

(X-Xb0)2+(Y-Yb0)2+(Z-Zb0)2=R2

(3)

将b1、b2、b3三点坐标带入式(3)，得到：

(Xb1-Xb0)2+(Yb1-Yb0)2+
(Zb1-Zb0)2=R2

(Xb2-Xb0)2+(Yb2-Yb0)2+
(Zb2-Zb0)2=R2

(Xb3-Xb0)2+(Yb3-Yb0)2+
(Zb3-Zb0)2=R2

因圆心在圆平面上，则可得到方程：

Ab1(Xb0-Xb1)+Bb1(Yb0-Yb1)+
Cb1(Zb0-Zb1)=0

(4)

将以上方程联立求解，可得到工件坐标系Yb轴的矢量为：

Yb=Lb0→b4×Zb=αbyi+βbyj+γbyk

(5)

其中，Lb0→b4为点b0到点b4的单位化向量。根据右手法则可知Xb轴的矢量为：

Xb=Yb×Zb=αbzi+βbzj+γbzk

(6)

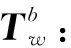
(7)

(8)

该方法只需保证工件中某一特征点对应，对基准圆上的任意三点没有任何要求，可广泛应用于具有圆形定位基准的工件。

1.2 正交平面六点标定法

图2为正交平面工件标定算法示意图，Ow-XwYwZw为机器人基坐标系；两个长方体从左到右分别处于由六点确定的仿真工作单元坐标系和实际工作单元坐标系。

图2 正交平面六点标定法

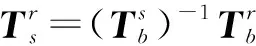
2 DXF离线编程技术

在对复杂工件进行标定时，因其本身因素会对标定精度产生影响，本文将工件DXF文件的提取与四点定位和六点定位标定方法相结合，使CAD坐标与工件的实际坐标统一，辅助了复杂工件的标定。

2.1 DXF文件的介绍

DXF(Drawing Exchange Format)文件是Autodesk公司推出的一个与外部CAD/CAM进行图形数据交换的接口，其内容以代码形式出现，是一种开放的矢量数据，组成部分如图3所示。

工件标定过程中所需图元信息包含在图形交换格式(DXF)文件中，一般的DXF文件数据信息量巨大，提取时应对文件进行筛选[6]。而标定所需的图形位置坐标信息只存在于实体段(ENTITIES)中，因此只对DXF文件内的实体段段进行提取即可[7]。

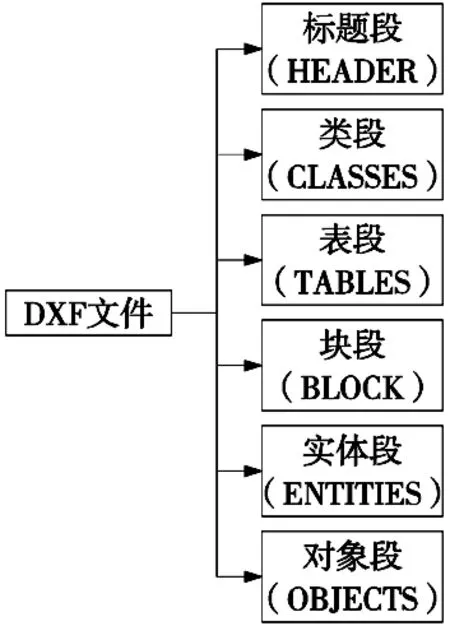
图3 DXF文件格式图

2.2 DXF数据提取流程

实体段信息的复杂程度由工件决定，为保证提取效率和识别的准确度，提取流程必须简洁高效，能够有条理、有选择的对实体段的信息进行提取整理[8]。

文件提取过程如图4所示，首先打开DXF文件对信息进行读取，当判断信息为实体段首行时，开始对四种图元类型依次判断，最后对厚度进行判断，当检测到文件信息为实体段尾时，关闭DXF，提取结束，最终可以得到机器人需要的参数信息。

图4 DXF数据提取流程图

2.3 DXF提取程序设计

常见的复杂工件中的图形信息基本都由直线和圆弧组成，所以程序的设计主要针对直线段与圆弧。

当用VC来设计DXF文件的读取[9]处理ASCII码时，需要用到C语言处理的两个标准函数：fprintf()和fscanf()。首先使用fopen()指令打开DXF文件，按照顺序读取到文件结束，然后利用位置指针函数fprintf()，标记当前位置。如需遍历完整文件，则按照位置顺序从上往下，读取完一个字符自动移到下一个字符的位置[10]。

下面以圆弧信息的提取为例：首先使用Str=ReadDxfFile(fp) 命令开始读取文件，依次判断读取处是否为实体段和圆弧信息段，随后确定圆心坐标X、Y、Z方向坐标值，然后判断圆弧半径组值、起始角度组值、终止角度组值，最后使用 If (str = "EOF") 命令判断是否为末尾，结束读取并退出。

提取直线段信息时将代码中的“ARC”更改为“LINE”，并判断直线的起始点和终止点坐标值，直线段起始点的X、Y、Z坐标组码与圆心坐标相同，分别为10、20、30，直线段终止点的X、Y、Z坐标组码分别为11、21、31，而圆弧的半径、起始角度、终止角度组码分别为40、50、51。提取后，机器人可以根据程序完成相应的动作。

以一具有圆弧和直线段的图形为例，用VC软件对DXF文件进行提取，后续在人机交互界面中输出提取形成的图形。图5为CAD软件中绘制的图形，图6为提取DXF文件生成的图形，可见DXF文件提取的方法完全符合精度要求。

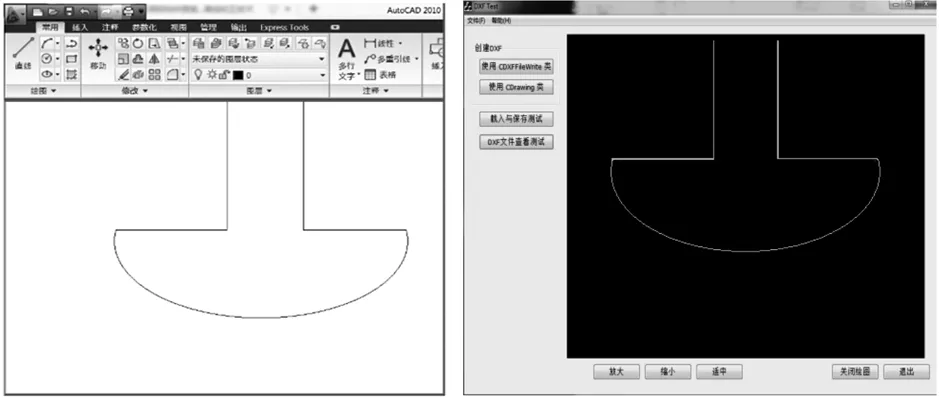
图5 CAD中工件图像 图6 DXF提取图像

3 相机标定实验

3.1 相机成像模型

相机成像模型是一种用来描述成像平面像点与空间物点之间数学投影关系的模型[4],图7为相机成像的几何模型，成像关系为线性变化。

图7 相机成像模型

视觉系统获取图像是一个比较复杂的过程，在描述获取图像与摄像头之间的关系时，一般在视觉系统中主要使用4种坐标系，如图所示，分别为：世界坐标系Ow-xwywzw、相机坐标系Oc-XcYcZc、图像物理坐标系o-xy和图像像素坐标系Op-uv。Op为相机的光心，O为成像主点。

世界坐标系中一点Pw在像素坐标系内的投影点Pp为Pw与成像平面的交点，二者的关系为：

其中，ax和ay分别为相机在x轴和y轴上的焦距，单位为mm，u0和v0为成像主点的坐标值，A为内部参数矩阵，M为外部参数矩阵。当世界坐标系中的一点投影到像素坐标系中，会发生很大变化，同时也会损失很多信息，因为镜头并不是理想的透视成像模型，都存在不同程度的畸变，因此必须要考虑相机畸变，所以有：

本文中考虑了镜头的二阶径向畸变n1、n2和切向畸变pu、pv，(xk,yk)为畸变后的坐标，(xu,yu)为畸变前的坐标。

3.2 相机内参优化

在对物体识别与定位的过程中需要对相机进行标定和参数优化。相机标定的方法有传统标定方法、自标定方法以及主动视觉标定方法[11-12]，一般使用传统标定方法较多，目前主要有线性标定法、Tsai两步法[13]、张正友标定法[14]等。其中张正友标定法操作简便可靠，对设备要求不高，被广泛应用。但该方法使用的传统优化算法易陷入局部最优，标定精度有待提高。相机标定作为视觉基础已有多种成熟的标定方法，本次标定使用张正友标定法，该方法是一种介于传统标定和相机自标定之间的标定方法。该方法对相机内参数初始值的求解已非常成熟，本文中不再赘述。大致标定过程为：选用棋盘格为标定参照物，保证相机固定，对棋盘进行不同角度的多次拍摄，将左右相机拍摄到的图片相对应，并对线条进行测量。利用已知的棋盘格角点坐标得到对应的图像坐标，即可求出单应矩阵。然后根据求得的单应矩阵和旋转矩阵R推出内部参数矩阵A，进而得到理论层面的内部参数与外部参数。

张正友标定法简单易操作、精度高、鲁棒性好，经过标准计算确定了理论上的可行性。但该方法未考虑实际应用中畸变与噪声的影响，因此需要把标定结果作为初始条件进一步优化。

假设相机在标定时采集到m张不同的棋盘格标定板图像，每幅图像包含p个角点，已知内部参数矩阵A、旋转矩阵R、平移向量s。令其中一个棋盘格角点为T，经过透视、旋转平移变换后得到一由A、R、s、T组成的函数，记t′，进而建立如下目标函数：

(9)

式中，t′为该角点的理论像素坐标，i表示图片的顺序数，j表示该图片上的角点顺序数，tij为第i幅图像上第j个角点的实际像素坐标，Ri、si分别表示第i幅图像的旋转矩阵和平移向量，Tj为第j个角点的坐标。由于理论像素坐标和实际像素坐标中的误差包含镜头畸变的影响，所以畸变参数应添加到目标函数得优化中，得到新的目标函数为：

(10)

至此，问题已转化为最小二乘法的线性优化问题，常用的传统方法有LM法、最速下降法等。

4 基于自适应权重粒子群算法的相机参数优化

4.1 基本粒子群算法

传统算法如LM法等在优化过程中易陷入局部最优，现提出一种改进粒子群算法，能有效避免优化过程中因算法过早收敛而陷入局部最优的问题。

粒子群算法(PSO)是进化算法的一种，从随机解出发，迭代寻找最优，通过适应度来评价解的品质。PSO算法精度高、易实现、收敛快，对种群数量和初始速度要求不高，全局搜索能力比传统算法更强，在解决实际问题中展现出其优越性。

PSO初始化为空间中的一群随机粒子，位置表示为矢量Xi，速度为矢量Vi，每个粒子都有一个由目标函数确定的适应值(fitness value),它们在寻找全局最优解时不断交流，将自己找到的最好位置(Pbest)传递给所有粒子，这样每个粒子就可得到当前群体中发现的最好位置(Gbest)，并通过自己的位置和同伴中最好的位置来决定下一步的运动。粒子的条件更新方程可以用下式表示：

(11)

式中，t代表当前迭代次数；ω代表惯性权重，为非负数；c1和c2自身和社会学习因子，一般取2；r1和r2为(0,1)区间内互不干涉的随机数。

4.2 改进粒子群算法

惯性权重ω在算法寻优时发挥着重要作用，其值较大时，算法的全局搜索能力强，局部搜索能力变弱，其值较小时相反。为避免算法过早收敛，我们令惯性权重随着粒子适应度而发生改变，创建了一种用于相机标定的自适应权重法，假设群体中初始粒子的个数设置为n，具体函数关系如下：

当F(xi)≤Fv时，

(12)

当F(xi)>Fv时，

(13)

其中，

(14)

其中，ωmin为惯性权重最小值，ωmax为惯性权重的最大值，F(xi)为第i个粒子的位置在目标函数式(10)中的值，Fmin为该次迭代F(xi)中的最小值，Fmax为该次迭代中F(xi)的最大值。迭代过程中，当粒子所处位置比其他粒子更优时，惯性权重值变小，使该粒子有较好的局部搜索能力，更快找到更优位置。当粒子位置较差时，惯性权重值变大，使粒子快速脱离该位置，转向全局搜索。这样可保证粒子在运动时既能向全局最优值靠拢，又能保持一定的全局搜索能力，避免粒子群在搜索的时候陷入局部最优。

4.3 相机标定参数优化结果

对12幅不同角度和位置的标定板图像进行采集，将角点网格进行提取并标定，得到的角点网格与相机位置关系图如图8所示。

图8 相机与棋盘格角点位置关系

标定选用焦距为8 mm的定焦镜头，实验用棋盘格标定板在X方向棋盘格数目为10，Y方向数目为7，单个黑白格尺寸为25 mm×25 mm。设置粒子群数目i=150，迭代次数t=400，惯性权重ωmax=0.8，ωmin=0.3，自身学习因子c1和c2=1.5，社会学习因子c2=2。

表1中为两种方法求得的相机内部参数，根据表中各项参数值来看，自适应权重粒子群算法在精确度上优于张正友标定法。为进一步验证两种方法的精确程度，需要对其重投影误差进行计算。

表1 相机内参标定结果

图9为张正友标定法重投影误差，图10为自适应权重粒子群算法重投影误差。可以看出自适应权重粒子群算法的精度更好，具有更高的可行性。

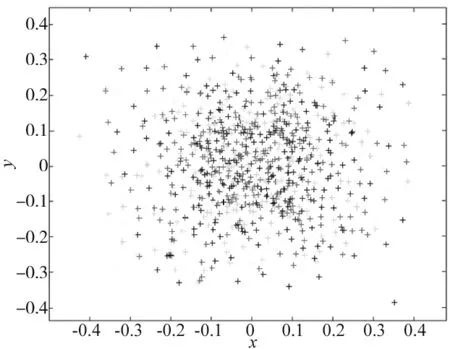
图9 张正友标定法重投影误差

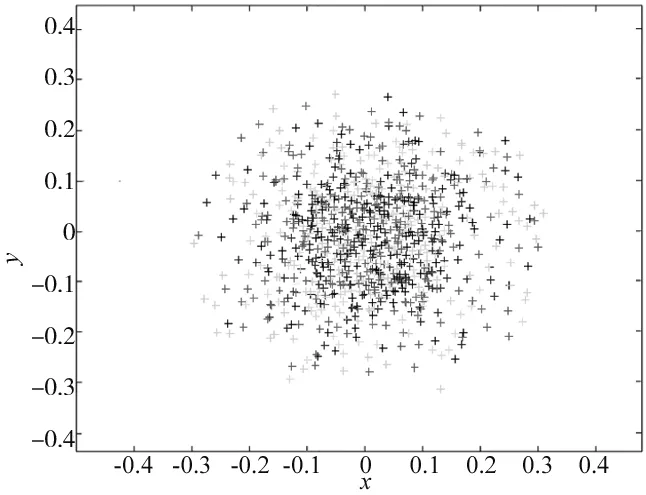
图10 自适应权重粒子群算法重投影误差

5 结论

为提高基于视觉伺服的工业机器人的工作精度，针对工件标定与相机标定环节分别提出了DXF提取辅助标定和基于自适应权重粒子群算法的相机内参优化方法，通过对DXF信息进行提取，为工件的标定提供了精准的图元坐标信息，实现了CAD单元与实际工作单元工件坐标信息的统一；建立添加了二阶畸变的相机模型，并通过张正友标定法确定了内参的初始值，创建了添加畸变的目标函数，然后使用自适应权重粒子群算法对目标函数进行优化，最后在标定实验中将该算法取得的参数和与张正友标定法中的传统优化方法进行了对比，并且对参数进行了重投影误差分析，结果进一步证明了自适应权重粒子群算法在相机内参优化过程中能取得更好的结果，有效的提高了标定精度，是一种可靠的方法。