基于改进粒子群算法的自由曲面轮廓度评定

万 润,王 琳,盛步云

(武汉理工大学 a.机电工程学院;b.湖北省数字制造重点实验室，武汉 430070)

0 引言

近年来，随着制造业的发展，自由曲面零件越来越广泛应用于汽车、飞机、大型船舶等工业领域。曲面的加工质量直接关系到产品的质量和使用寿命，因此对自由曲面零件进行高效率与高精度的检测和轮廓度误差评定有着重要的研究意义[1]。

对于复杂曲面轮廓度的评定，依据算法原理主要可以分为二类，一类是基于最小二乘原理，最具代表性的是在1992年提出的最近点迭代算法[2]，常用于曲面定位问题中。一类是基于最小条件的最小区域法，要求包容全部测点的理论曲面等距面的距离最小，由于一般曲面的表达式未知，且计算量复杂，多采用启发式优化算法解决这类非线性优化问题，如遗传算法、粒子群算法[3-4]等, 但遗传算法在进行轮廓度误差评定时，由于局部搜索性能较差，容易产生早熟收敛的问题，而且在进化后期搜索效率不高，在解决大规模计算量问题上比较费时；而粒子群算法在运算后期则容易陷入局部最优。

在确定最小包容区域过程中，测量点到曲面的距离计算也是其中一个重要的问题[5-6]，文献[5]用网格划分曲面，通过不断细分网格来逼近测点到曲面的实际距离，但必须已知曲面的函数表达式且计算过程复杂，难以平衡计算精度和效率，文献[6]把空间点到自由曲面距离转化为点到STL模型的有向距离，但没有考虑到出现狭长三角面片的情况，存在适应性缺陷。

为解决以上问题，本文采用一种基于天牛须搜索的粒子群优化算法，以测点集与理论轮廓面达到最佳匹配为目标，寻找一组平移、旋转变换矩阵来确定理论曲面的最小包容区域，并且针对出现狭长三角面片的情况做了优化处理，进一步简化了测点投影点与三角面片关系判定条件，提高了算法的实用性和适应性。

1 自由曲面轮廓度评定模型的建立

1.1 曲面轮廓度误差的定义及关键步骤

根据GB/T 1958-2004，轮廓度评定要求满足最小条件原则，即所有测量点均位于上下两包络面边界所限定的包容区域内，且包容区域的宽度或直径为最小，其误差值是包容被测曲面轮廓且距理论曲面轮廓法向距离最小的两曲面间的宽度。

轮廓度评定一般需要解决两个关键步骤的问题，一是计算测点到复杂理论曲面的最小距离，二是建立复杂曲面轮廓度误差评定的数学模型并求解。针对步骤一，将曲面CAD模型转换为STL模型，测点到曲面的最小距离就简化为寻找距离测点最近的三角面片的问题；针对步骤二，根据最小条件原则和齐次坐标变换理论建立相应的轮廓度评定数学模型，并应用基于天牛须的改进粒子群算法求解。

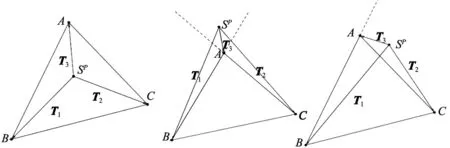
图1 曲面轮廓度误差示意图

1.2 点到自由曲面STL模型最短距离计算

STL模型是通过一系列三角面片来逼近CAD模型的，其数据文件主要包含二进制和文本两种格式，主要描述三角面片的顶点坐标数据信息和单位法矢量数据信息[7]。文献[6]通过判断测点投影点与STL模型三角面片的位置关系，来求取其到曲面的最短距离，相较于传统的需要已知曲面表达式的分割逼近法适用性更高。但存在两点不足，一是投影点与三角面片位置关系的判断条件不够简化，二是如果STL模型中存在狭长的三角面片，则以测点到三角面片顶点的最近距离为择优目标筛选出的三角面片集不一定包含距离测点最近的三角面片，导致算法失效。针对上述不足一，采取向量运算代替相对繁琐的角度量计算，将投影点与三角面片关系整体分为三类情形来判断，针对不足二，选择测点到三角面片顶点和中心点两者之间的最小距离，综合筛选三角面片集。

计算测点到自由曲面距离的具体步骤如下：

步骤1：计算测点Pi(xi,yi,zi)到每个三角面片顶点及中心点的距离，标记距离最近点为Qi点。

步骤2：如果点Q为三角面片顶点，则搜索以Q点为顶点的所有的三角面片并放入集合S内；如果点Q为三角面片中心点，则搜索与该三角面片共顶点的所有三角面片并放入集合S内。

步骤3：分别计算测点Pi到集合S内三角面片的距离，依据测点投影的位置，测点到三角面片的距离计算有以下三种情形：

情形1：投影点Sp在三角面片内部，此时测点P到三角面片的最短距离就是测点P到投影点Sp的距离。

情形2：投影点Sp在三角面片外部，但处于三角形某一边延长线与另一边延长线的区域范围内，此时最短距离就是测点到这两条边的共顶点的距离。

情形3：测点投影在三角面片外部，但处于三角形某一边与另一边延长线的区域范围内，此时测点P到三角面片的最短距离就是测点到三角面片上该边的距离。假设投影点Sp的位置不满足上述两者的情形，则必然满足情形3，只需计算测点P到三角面片三条边的距离，其中最小值即为测点到该三角面片的最短距离。

按照以上3步计算点到所有三角面片的距离，以最小值作为点到曲面距离。

(a) 情形1 (b) 情形2 (c) 情形3图2 投影点和三角面片关系示意图

1.3 曲面轮廓度评定的数学模型

由于在实际测量过程中存在系统误差，测量坐标系与设计坐标系难以完全重合，测量曲面相对于理论曲面会有一定的偏移与扰动。依据最小条件原则，只有当测点集与理论轮廓面达到最佳匹配时，才能使包容所有测量点的两理论等距曲面之间的距离最小，因此必须对测点集进行刚性平移、旋转坐标变换，使得最大变动量最小化。设实测曲面上的测点为pi(xi,yi,zi),i=1,2,…,n，其中n为测量点数量，其坐标变换矩阵为：

T=Trans(δx,δy,δz)Rot(x,α)Rot(y,β)Rot(z,γ)

(1)

式中，平移变换矩阵为：

(2)

旋转变换矩阵为：

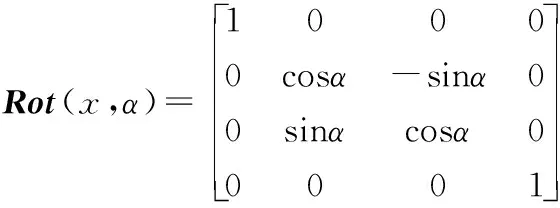
(3)

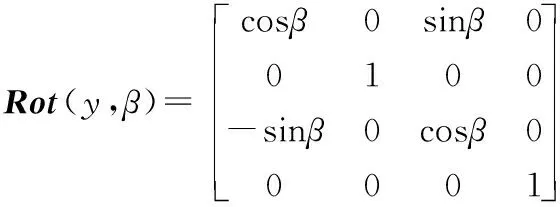
(4)

(5)

其中，δx,δy,δz为实际加工曲面沿理论曲面坐标系x,y,z轴的平移量，α,β,γ为实测曲面绕理论曲面坐标系x,y,z轴的旋转量。

测量点经过坐标变换后的新坐标为：

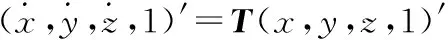
(6)

则最小区域法评定复杂曲面轮廓度误差的数学模型为：

f=min{max[2di(δx,δy,δz,α,β,γ)],i=1,2,3,…,n}

(7)

其中，di(δx,δy,δz,α,β,γ)为测点到理论设计曲面的距离，由模型可以看出，轮廓度误差的评定过程实质上是一个多元非线性寻优过程，要求寻找一组最优的变换参数，使所有测点到曲面的最大距离最小。

2 基于天牛须搜索的粒子群优化算法

2.1 BAS算法(天牛须)

天牛须搜索算法是2017年提出的一种高效的智能优化算法[8]，当甲虫捕食或寻找猎物时，它会用两只触角随机地探索附近的区域，当位于一侧的触角探测到高浓度的气味时，甲虫就会转向同一侧，否则，它就会转向另一侧。双触角甲虫的搜索行为可以与待优化的目标函相关联，从而形成新的优化算法。和遗传算法、粒子群算法等智能算法类似，相比较传统的微分类优化算法，天牛须算法同样可以在缺乏具体的函数表达式和最快下降方向等信息基础上实现高效寻优与求解。具体的算法流程如下：

(1)假设天牛可以随机向任何方向前进，随机生成方向向量，标准化：

(8)

其中，n为待优化参数的维度。

(2)计算天牛左右须的坐标也即左右触角的位置：

xtr=xt+dtb
xtl=xt-dtb

(9)

其中，xt为t时刻天牛的位置，dt是t时刻天牛质心到触须的距离，xtl为第t次迭代时的左侧触须坐标,xtr为第t次迭代时的右侧触须坐标。

(3)根据左右两须对应的函数值，决定天牛下一时刻移动位置：

xt+1=xt+δtbsign(f(xtr)-f(xtl))

(10)

δt为t时刻的步长，f为待优化目标函数，sign代表符号功能。

(4)步长与搜索距离更新：

dt=ηddt-1+d0
δt=ηδδt-1

(11)

ηd和ηδ分别为搜索距离和步长的更新衰减系数，d0表示两触角之间的初始距离。

2.2 基于天牛须搜索的改进粒子群优化算法

粒子群算法虽然在收敛速度上具有优势，但侧重于种群和粒子本身的历史经验对每一个粒子的影响，而忽略了在搜索过程中粒子自身对空间环境的判断，也无法对粒子的速度进行动态的调节，容易陷入局部最优。针对上述问题，可以选择引入天牛须的思想提高粒子的自主寻优和全局搜索能力[9-10]。

相较于标准粒子群算法，基于天牛须搜索的改进粒子群算法中的每个粒子就相当于BAS中的一只天牛，虽然其初始位置和速度不变，但在每次的迭代过程中，天牛位置的更新规则不再只由历史最优值和当前全局最优值所决定，而是引入天牛须搜索的思想，添加了天牛自身对周围环境的判断。

(1)位置更新时，按照PSO和BAS的方式各自更新后加权得到新的位置。也就是，利用了BAS的触须方向和步长，同时也利用了粒子的速度：

(12)

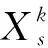
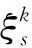
(13)

曲面轮廓度评定的具体过程如下：

(1)初始化参数，设置种群规模为N，最大迭代次数n，参数维度m，位置更新权重λ，初始步长d0，触须之间长度初始值d1。

(2)随机初始化天牛的位置x和速度v，确定适应度函数，获得天牛群体的个体最优值和全局最优值。

(3)根据式(12)和式(13)计算天牛的下一步位置与速度。

(4)更新天牛搜索步长和两触须之间的长度，并计算更新后的天牛群的个体最优值和全局最优值。

(5)判断是否满足迭代终止条件，若满足，则返回当前全局最优值，否则返回步骤(3)继续搜索，直至达到最大迭代次数。

3 仿真分析

为了测试改进后的粒子群算法对比标准粒子群在评定曲面轮廓度上是否有更高的准确性，选用自由曲面一进行仿真实验，该STL模型由242个三角面片和165个顶点构成。在曲面上均匀选取400个理论测点，考虑到存在的系统误差，将理论测点沿x,y,z轴平移0.1 mm、0.3 mm、-0.6 mm，逆时针旋转-0.05 rad、-0.04 rad、0.07 rad，并添加服从正态分布N(0,0.04)的随机性矩阵作为加工误差，得到模拟实测点集。即：

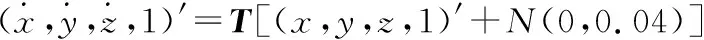
(14)

其中，

设计曲面和仿真测点分布如图3a所示，图3b为改进后的粒子群算法完成模型求解后重新定位的测点分布，6个最优变换参数结果如表1所示。

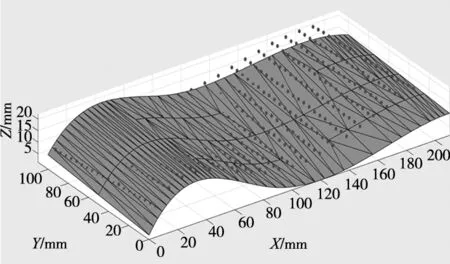
(a) 定位前的测点分布

(b) 定位后的测点分布图3 自由曲面一仿真测点定位前后分布图

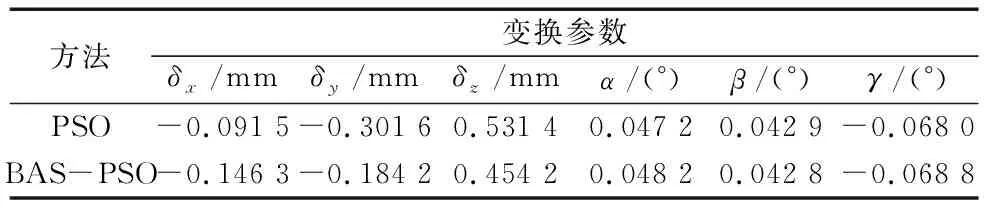
表1 自由曲面一定位的6个参数

选用自由曲面二进行仿真实验，该STL模型由1776个三角面片，954个顶点构成。在曲面上随机选取400个理论点，添加系统误差e=[0.1,0.2,-0.1,-0.01,-0.02,0.02]，同样添加服从正态分布N(0,0.04)的随机性矩阵作为加工误差，得到模拟实测点集合。设计曲面和仿真测点分布如图4所示，图4b为改进后的粒子群算法完成模型求解后重新定位的测点分布，6个最优变换参数结果如表2所示。

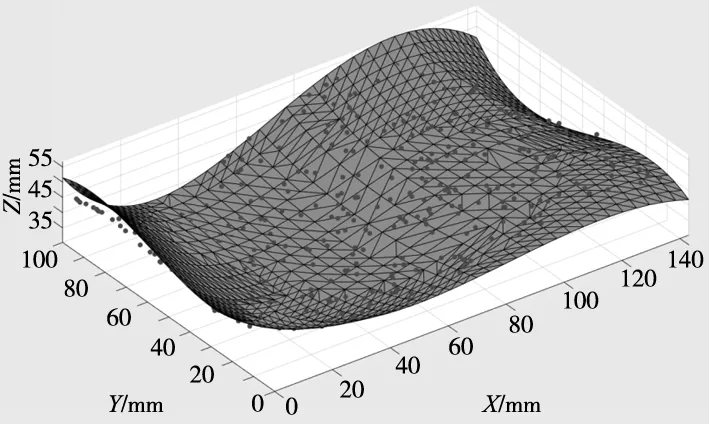
(a) 定位前的测点分布

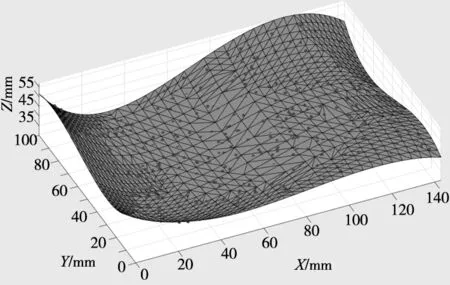
(b) 定位后的测点分布图4 自由曲面二仿真测点定位前后分布图

表2 自由曲面二定位的6个参数

根据测点到曲面的距离模型计算轮廓度误差，对于自由曲面一，改进后的粒子群算法和粒子群算法求得的轮廓度误差分别为1.130 8 mm和 1.136 7 mm。如果是均匀提取100个点作为理论测点，则计算的轮廓度误差分别是0.951 4 mm和1.036 1 mm。对于自由曲面二，改进后的粒子群算法和粒子群算法求得的轮廓度误差分别为1.226 1 mm和 1.262 0 mm。由以上两个实验可知基于天牛须搜索的改进粒子群评定的曲面轮廓度结果更加精确。

4 结束语

为了提高曲面轮廓度评定结果的准确性，建立了轮廓度误差评定的数学模型，并采用引入天牛搜索思想的改进粒子群算法进行求解。将测点到自由曲面的距离转化成测点到STL模型的距离，并对于存在狭长三角面片的情况作了补充处理，同时也简化了测点投影点与三角面片关系的判断条件。通过仿真实验验证与对比，采用基于天牛须搜索的粒子群算法相对于标准粒子群可以有效提高曲面轮廓度误差的评定精度。

DOI：10.5430/ijrc.V1n1p1.