基于Petri网的高校网上预约报销系统的建模与优化

方新升， 刘祥伟

( 1.安徽理工大学 数学与大数据学院； 2.安徽理工大学 经济与管理学院: 安徽 淮南 232001 )

0 引言

Petri网由于可以用图形化的方式描述业务流程中的每一个活动，使人们可以直观地发现流程中所存在的问题，因此它在众多领域中得到应用.例如：文献[1]使用Petri网对云制造的相关流程进行了建模分析，并通过实例证明了该模型的有效性；文献[2]提出了一种将分布式锁与Petri网结合的方法，该方法可以简化锁的管理过程；文献[3]针对入侵检测流程，提出了一种将面向对象和Petri网相结合的检测方法，并通过实验证明了该方法可以有效降低检测的误警率；文献[4]提出了一种具有优先权Petri网模型，并通过实例证明了该模型具有实时处理新数据的能力；文献[5]提出了一种将离散Petri网和连续Petri网相结合的Petri网，并通过对比模型间的误差变化验证了该模型的合理性；文献[6]提出了一种分布式模糊推理Petri网，并通过仿真实验证明了该Petri网可显著降低系统的负载；文献[7]针对行为等价的不恰当性，提出了一种基于行为轮廓的一致性对齐概念，并通过推导和计算证明了一致性在模型对齐中的作用.近年来，随着计算机网络技术的不断发展，国内大部分高校的财务部门已开始使用网上预约报销系统进行报账.为了提高高校财务部门网上预约的报账效率，一些学者对其进行了研究，如章杰文等[8]使用作业成本法设计了一种高校网上预约报销系统，但目前还未见采用Petri网对其进行研究的文献报道.为此，本文基于高校网上预约整体流程的排队问题，利用Petri网和活动间的行为轮廓关系，提出一种高校网上预约报销系统的优化模型，并通过PIPE和Tina软件对优化模型的合理性进行了验证.

1 基本概念

定义1[9]满足下列条件的三元组N=(S,T;F)称作一个网： ①S∪T≠∅; ②S∩T=∅; ③F⊆(S×T)∪(T×S); ④ dom(F)∪cod(F)=S∪T.其中： dom(F)={x∈S∪T|∃y∈S∪T:(x,y)∈F}, cod(F)={x∈S∪T|∃y∈S∪T:(y,x)∈F}.

定义2[9]设Σ=(S,T;F,M)为一个Petri网.如果存在t∈T, 使M[t>M′， 则称M′为从M直接可达的.如果存在变迁序列t1,t2,…,tk和标识序列M1,M2,…,Mk使得M[t1>M1[t2>M2…Mk -1[tk>Mk则称Mk为从M可达的.从M可达的一切标识的集合记为R(M)，并约定M∈R(M).

定义3[9]一个网系统是一个标识网Σ=(S,T;F,M)， 并具有如下变迁发生规则：

1)对于变迁t∈T， 如果∀s∈S:s∈·t→M(S)≥1则变迁t在标识M有发生权，记为M[t>.

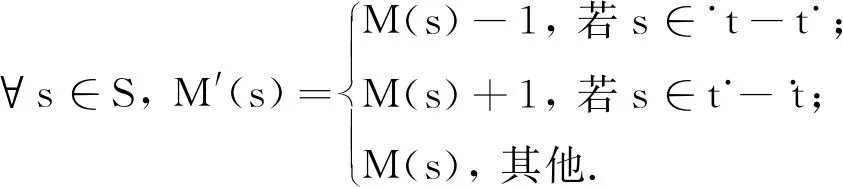
定义4[10]设(N,M0)是一个Petri网，其初始标识为M0， 且对任意的(t1,t2)∈(T×T)该Petri网满足如下关系：

1)若t1>t2且t2≯t1， 则称t1和t2为严格序关系，记作t1→t2；

2)若t1≯t2且t2>t1， 则称t1和t2为严格逆序关系，记作t1→-1t2；

3)若t1≯t2且t2≯t1， 则称t1和t2为排他序关系，记作t1+t2；

4)若t1>t2且t2>t1， 则称t1和t2为交叉序关系，记作t1||t2；

5)将所有关系的集合称为行为轮廓，记作BP={→,→-1,+,||}.

2 基于Petri网的网上预约报销系统的优化分析

高校网上预约报销的基本流程包含以下活动：选择报销模板并填写(t1)、登录预约报销系统(t2)、填写基本信息(t3)、选择报销类型(日常报销、科研入账等，t4)、在线排队(t5)、获取排队号码(t6)、名额已满(t7)、报销(t8)等.其中：从选择报销模板并填写到在线排队为顺序关系，即变迁序列(t1t2t3t4t5)依次发生；当排队名额未满时分配一个排队号码，当名额已满时返回到s3， 即获取排队号码和名额已满是排他关系(t6+t7)； 当获得排队号码后，报销(t8)发生，即完成报销流程.高校网上预约报销系统的基本Petri网模型如图1所示.

图1 高校网上预约报销系统的基本Petri网模型

由于高校网上预约报销整体模型(下文简称“整体模型”)是在高校网上预约报销系统基本模型(下文简称“基本模型”)上扩展得到的，因此整体模型比基本模型更为详细和具体.图2为某高校的整体报销模型.由图2可以看出，整体模型与基本模型的区别有以下几点： ①整体模型将登录系统操作细分为新用户注册登录(t2)和老用户直接登录(t3)， 两者是一种排他关系，即(t2+t3).②根据财务处工作人员的工作时间，整体模型给每个报销人员分配了一个报销时段，当分配的时段超出财务处工作人员的工作时间(t10)时则需要报销人员在第2天重新排队，即返回到s3； 当分配的时段未超出财务处工作人员的工作时间(t9)时则可继续执行下一个活动，进入等待叫号(t11)的状态.③针对报销人员能否在指定的时段内到达报销地点的问题，整体模型将其分为2种情况：如果报销人员未在分配时段内抵达(t13)报销地点时，则需要报销人员在第2天重新排队，即返回到s3； 如果报销人员在分配时段内抵达(t12)报销地点时，则正常进入下一步骤.

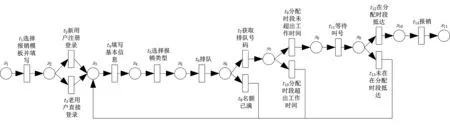
图2 某高校网上预约报销系统的整体Petri网模型

由以上整体模型可知，该流程中存在以下问题： ①整体模型没有限制报销人员获取号码的次数，即一名报销人员可以多次获取号码，这可能会导致出现恶意获取号码的情况，进而会使得其他报销人员无法正常获取号码.②整体模型没有考虑到当天排队人数过少的情况，不利于提高财务部门的报账效率.③整体模型没有考虑到排队号码靠后的报销人员的报销问题，因此排队号码靠后的报销人员可能会因为报销时段超出工作人员的工作时间而导致号码作废，进而使得报销人员需要在第2天重新排队获取号码.

根据整体模型中存在的问题，本文结合活动间的行为轮廓关系提出了高校网上预约报销系统的优化模型(下文简称“优化模型”)，如图3所示.本文提出的优化模型主要从以下几个方面对整体模型进行优化： ①为了避免恶意获取号码现象的发生，添加了报销记录检测(t6)， 即如果报销人员近两日内无报销完成记录则进入正常的排队状态(t8)， 如果报销人员两日内有报销完成记录(t19)则进入下一个检测环节.②为保证不出现当天报销人数过少而降低报账效率的情况，添加了今日排队人数的检测(t20)， 即如果当日的排队人数大于给定阈值时则无法进入排队状态，如果当日的排队人数小于阈值时则为有记录的报销人员分配靠后的号码(t23).③为了保证排队号码靠后的报销人员能够顺利地完成报销，为分配报销时段超出财务处工作时间的报销人员分配一个第2天前20位的号码(t13).

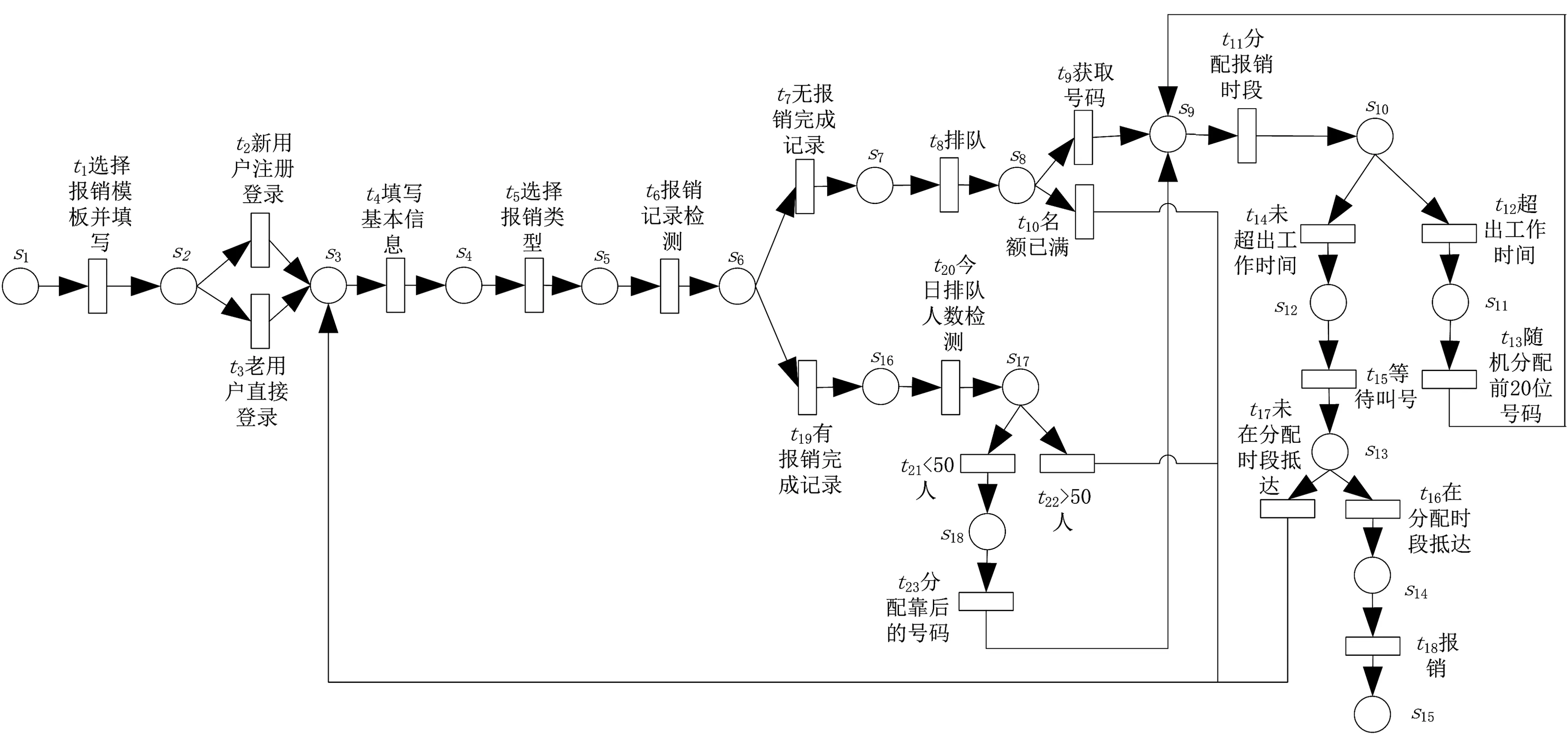
图3 高校网上预约报销系统的优化Petri网模型

3 优化模型的仿真模拟

图4 基于PIPE软件的优化模型的状态分析测试结果

为了验证优化模型的可达性和合理性，本文采用PIPE和Tina软件对优化模型进行模拟仿真实验.PIPE软件是一种基于JAVA环境的仿真软件，能够检测Petri网模型的安全性、活性、死锁等问题.Tina软件是一种偏向于时间Petri网的测试软件，能够分析不同时刻时的模型状态.本文测试主要是通过在起始库所添加一个token的方式来测试优化模型是否可以正常运行以及能否达到预期的效果.图4是基于PIPE软件的优化模型的状态分析测试结果，图5是基于Tina软件的优化模型的状态分析测试结果，图6是基于Tina软件的优化模型的结构分析测试结果.由图4—图6可以看出，优化后的模型是有界、安全的.

图5 基于Tina软件的优化模型的状态分析测试结果

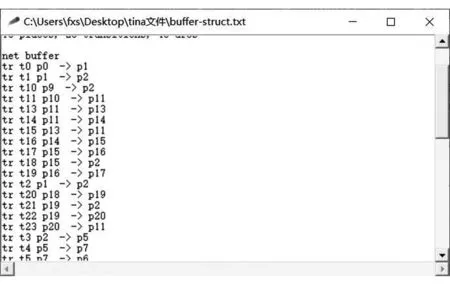
图6 基于Tina软件的优化模型的结构分析测试结果

4 结语

本文基于Petri网和行为轮廓关系对高校网上预约报销流程进行了建模和优化.实验表明，本文提出的优化模型不仅可以保证每一名报销人员都能够顺利地完成报销，而且还可以提高财务部门的工作效率，同时在报账过程中可以避免报销人员恶意多次获取号码的现象发生.由于本文只是从模型的角度对预约报销流程进行优化，所以该优化模型存在一定的局限性，今后我们将结合更多的实际情况对流程做更进一步的分析和优化.