浅谈“两化改正”对矿山井下导线测量精度的影响
刘彩霞,刘 轩,李 芳
(1.金川集团股份有限公司三矿区,甘肃 金昌 737100;2.金川集团股份有限公司二矿区,甘肃 金昌 737100)
测量工作是一项精而细的工作,在精度方面尤为重要,精度的高低直接决定着矿井的安全生产,因此提高测量精度,减少测量工作量,是测量工作者不断探讨和研究解决的主要课题。同时,测量工作也是一项及其复杂的工作,存在很多误差,外业测量都是在地面进行的,观测数据的基准线是各点的垂线,而内业数据处理的基准线是参考椭球面上的法线,由于存在垂线偏差,故需要将外业测量的数据归算到参考椭球面上。为了便于测量计算和生产实践,我们还需要进行高斯-克吕格投影(简称高斯投影),将椭球面上的元素化算到高斯平面上。
因此,在进行高等级导线测量时,观测地面同椭球面和椭球面同高斯平面之间的“两化改正”就显得很有必要。但是,在小范围内进行由量边误差引起的井下四等支导线点位中误差估算时,导线“两化改正”前后的测距误差对终点点位误差计算结果是否有影响呢?本文结合自身工作实际,以金川某矿区东部贫矿为例,浅析对于井下低等级导线,计算由量边误差引起的支导线终点点位误差时,是否有必要进行“两化改正”。
1 井下支导线实测
在金川某矿区东部贫矿1330分段井下选择一照明、通风及作业环境良好的大巷,按设计施工图纸计算出各点的放设要素,然后利用全站仪进行各导线点的放设。
各导线点放设完成后,对各点位进行实测检核,⑨-㉞为起始已知边,在⑨点上架设全站仪,后视㉞,然后分别量取导线边⑨-㉞、⑨-⑧的距离,然后转站在导线点⑧上架设全站仪,后视已知导线点⑨,量取导线边⑧-⑦的距离,如此依次测得各导线边的长度。各点间距离测量结果如表1所示。

表1 各导线点间的实测距离
2 “两化改正”前终点㊾的点位误差计算
大巷导线为一条支导线,由量边误差所引起的导线终点的点位误差计算公式:

光电测距误差计算公式为:

式中:A—固定误差;B—比例误差;D—实测边长。
按四等导线计算,根据《工程测量规范》,A=5mm,B=5*ppm,代入(2)式得 :

按公式(3)对支导线各边的测距误差计算结果如表2所示。

表2 支导线各边的测距误差
将表(2)中各测距误差代入(1)式得:

则“两化改正”前由测距误差引起的终点㊾的点位误差为:
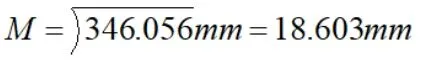
3 “两化改正”后终点㊾的点位误差计算
(1)由实测高程面归化到参考椭球面的距离计算。
改正数计算公式为:
日常工作中测定的高程一般都是正常高,表现为该点的铅垂方向,大地高表现为该点的法线方向,这两方向的偏差即为垂线偏差,但由此引起的高程异常值不超过±1mm,完全可以忽略。
故可以直接用实测的正常高代入(4)式进行计算。计算结果如表3所示。

表3 归化后椭球面上的距离
(2)由椭球面归化到高斯投影面的距离计算。
改正数计算公式为:


式中:ym—测站与照准站东西方向坐标平均值;Si—椭球面上的边长;R—平均曲率半径,取6371km。
计算结果如表4所示。

表4 “两化改正”后高斯投影面上的距离
4 “两化改正”后终点㊾的点位误差计算
将表4中的距离值代入(3)式中得“两化改正”后各边的误差,如表5所示。

表5 “两化改正”后各边的误差
根据表5中的数据计算得“两化改正”后支导线终点点位误差为
5 结论
通过实际测量金川某矿区东部贫矿1330分段部分大巷支导线的边长,估算由测距误差引起的终点点位误差,比较“两化改正”前后量边误差对支导线终点点位误差的影响,得出如下结论:“两化改正”前由量边误差引起的井下四等支导线终点㊾的点位误差为18.603mm,“两化改正”后由量边误差引起的四等井下支导线终点㊾的点位误差为18.602mm,“两化改正”前后由量边误差引起的四等支导线终点㊾的点位误差几乎没变。由此可知,在小范围内进行由量边误差引起的井下四等支导线点位中误差估算时,导线“两化改正”前后的测距误差对终点点位误差估算结果影响甚微,所以,井下低等级支导线精度估算时可以不用考虑“两化改正”,即可满足日常精度要求。

