一种基于TSV的3D存储器裸片优选堆叠方案

涂哲

（美国波士顿大学）

1 研究背景及意义

基于TSV 的三维集成电路是应对摩尔定律失效问题的重要技术途径之一，基于TSV 的三位集成电路主要应用于高密度芯片产品和异质集成应用领域，存储器类产品是典型的具有高密度的产品之一，因此基于TSV 的三维存储器受到了广泛重视。

然而，存储器不可避免的存在各类故障，因此在三维存储器中如何进行故障修复是一个对提高成品率具有重要作用的研究发现。邻近层冗余资源共享策略在修复率方面优于冗余资源层间全局共享和独立层内自修复[9]。

三维存储器由多个存储器裸片堆叠而成，每一个裸片在设计时会增加冗余行、冗余列资源，用于故障修复。通过合理匹配堆叠顺序，即便某层裸片中的冗余资源不足以修复本层中的故障，也可通过借用邻近层中的冗余资源达到故障修复的效果，从而使整体良率大幅提高，因此，裸片匹配技术具有重要研究价值。针对此问题学者们已经给出了一些方案，比如说文献[4]中Xu 等人提出了适用于两层冗余共享结构的匹配方案，并有效提升了三维存储器的成品率[4]；文献[3]中Lee 等人提出了全局冗余共享的方法,而TSV 的数量使用过多[3]；文献[1]中Zhu 等人则提出了邻近层冗余资源共享的方案。比较后，因为邻近层共享的高修复率，本文仅考虑邻近层共享策略下的裸片匹配问题，在现有的邻近层共享的方案中，只有Zhu等人的方案进行对比，虽然他们的方案在一定程度上提高了堆叠成品率，但在裸片的匹配策略上还有优化的余地，所以本文希望提出一种新的高效的裸片匹配方法，进一步提高三维存储器的成品率。

2 优化方案

2.1 优化方案简述

方案大概流程分为两个阶段，第一个阶段为堆叠前测试存储裸片的故障数，并基于ESP 算法平衡使用行列冗余资源针对故障进行模拟修复得到各个芯片所需的行列冗余资源，第二阶段开始堆叠，针对第一阶段得到的数据进行合理堆叠，以此来充分利用裸片冗余及层间共享策略最大化成品率，其中主要的策略在于冗余资源与故障数的匹配。

2.2 优化堆叠

在文献[1]算法的基础上，有更加优化，更加效率的算法。文献[1]的算法在第一阶段的测试与识别中，并没有详述其测试过程，而本文在第一阶段中讲述了识别时使用的ESP 算法，并且添加了冗余资源与资源需求的自适应匹配，而在第二阶段中，文献[1]虽然最大化利用了故障数偏大的裸片进行堆叠来提高成品率，其代价则为较为严格的筛选条件淘汰掉了部分故障数偏大的裸片，而如果将故障较少的裸片与故障较多的裸片进行组合来进行邻近资源共享则可以进一步拓宽裸片的选择面，使得更多的裸片成功堆叠，并且本文的堆叠算法中同样使用了冗余资源和资源需求的自适应匹配，使得冗余资源的利用率最大化，来进一步提升成品率。

2.2.1 堆叠前的测试与识别

假设每个裸片有行冗余RR，列冗余CR，存储器堆叠层数为L，测试出裸片中所含的行列故障以及正交故障，并针对使用ESP 算法来进行所需冗余资源数的识别。

ESP 算法的实现在于，当我们通过测试得到每个裸片所包含的行列故障以及正交故障后，使用行列冗余资源对其进行模拟修复，此时可以得知相应资源所能针对模拟修复的行列故障及正交故障数，接着对每个冗余资源模拟修复的故障数进行降序排列。

排序后，优先使用修复故障数较多的冗余资源，模拟修复后由于部分故障已被修复，则需重新测试裸片得到新的排序，重复以上步骤直到所有故障被修复。

在模拟修复过程中，需要强调的是资源与故障数的自适应匹配，在遇到正交故障或可修复故障数相等时，判断行冗余与列冗余使用数量，被使用数量较少的一方优先用于修复正交故障；而当预设的行列冗余数不相等时，优先使用预设冗余数较多的一方；算法结束后，得到修复裸片所需行冗余数量RF，列冗余数量CF，并得到每个裸片所修复的故障数F。

假设预先分配的冗余资源为4 个行冗余及4 个列冗余，在修复过程中，遇到了行列冗余都可修复三个故障的情况，而此时在之前的修复中已经使用了2 个行冗余及1 个列冗余，因为列冗余使用较少，则优先选择使用列冗余进行修复；而若预设冗余资源为4 个行冗余及5 个列冗余，则类似情况下都优先使用较多的列冗余资源进行修复，因为在整体的修复框架下，每一个裸片所富余的列冗余积累起来数量很大，因此优先使用。ESP 算法流程图如图1所示。

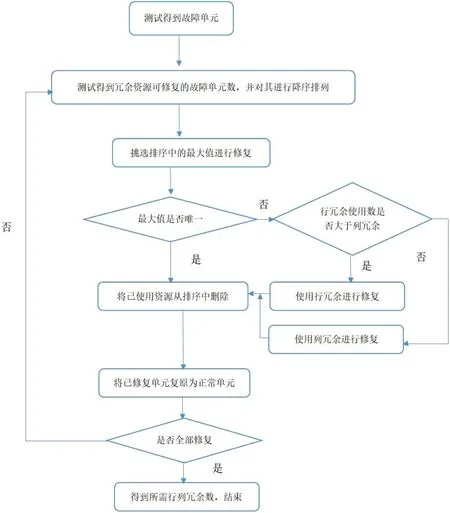
图1：ESP 算法流程图

2.2.2 堆叠裸片

通过测试与识别得到每一个裸片修复所需行列冗余资源的数量后，接着就是进行裸片的堆叠。假设每个裸片都有RR 个行冗余以及CR 个列冗余，每个存储器都有L 层，可供堆叠的裸片则有N 个，在ESP 算法中，重点强调的资源与故障匹配的思想在堆叠算法中也同样适用，其主要作用在于当预设行列冗余不相等时，假设行冗余为3，列冗余为4，当其他条件相同时，则优先考虑需要更多列冗余修复的裸片，或当预设冗余资源相等时，且其他条件相同时，优先使用行列冗余数最为接近的裸片。

首先，需要抛弃所需资源数RF 和CF 大于存储器中所有层数冗余资源数之和的裸片，即为RF>L*RR 或CF>L*CR 例如，存储器为4 层，每层裸片分配2 个行冗余及2 个列冗余，当裸片的RF或CF>8 时，此裸片需要被直接抛弃。

接着降序排列剩余N 裸片的修复所需行列冗余资源数之和S，从排序中挑选出S 最大的裸片i，当有多个裸片S 相等且预设冗余相等时，优先使用行列冗余数最接近的裸片，例如，一个裸片需要2 个行冗余及4 个列冗余进行修复，另一个裸片则需要3 个行冗余及3 个列冗余进行修复，两片的所需资源数之和都为6，而第二片所需的行列冗余数更接近，则优先选择第二片进行堆叠，或当S 相等预设冗余资源不相等时，如行冗余比列冗余更多时，优先匹配所需行冗余更多的裸片。以上做法的逻辑在于当S 相等且预设冗余相等时，由于预设行列冗余是相等的，则当进行匹配时，行列冗余数更接近的裸片成功修复的可能性更大，如果匹配的裸片所需的行列冗余数差距过大则容易导致后续修复时行或列冗余不足，而另一类型的冗余仍有富余的情况；而当S 相等预设行列冗余不相等时，则所有裸片积累的两种类型的冗余资源数差距是极大的，则匹配时优先选择所需冗余类型更为富余的裸片进行匹配能最大化的利用该差距。

接着从排序的底端依次挑选出两片故障最小值与i 进行匹配，需要强调的是，因为首层裸片仅能使用本层及一片邻层裸片的冗余资源，则需要将所需资源较小的放置在存储器的首层，而裸片i 次之，第三层再是另一片所需资源较小的裸片，选出两片所需资源数为最小值的裸片后，分别得到两个裸片所需行冗余及列冗余之和，分别为RS 和CS，而前三层堆叠时需要将行列冗余资源数进行分别处理，因为裸片i 所能使用的资源总值为3 层的冗余资源，如果裸片i 能完成修复则需要满足条件

RF<=3*RR-RS

CF<=3*CR-CS

如果匹配成功，则继续进行堆叠，并得到行列冗余使用数之和RS，CS；如果匹配失败，则将裸片i 从排序中去除，再重新进行堆叠。

前三个裸片堆叠成功后，接下来的裸片i 为排序中所需资源数之和最大值，当i=L 时，因为前面的裸片已经使用了RS 和CS 数值的冗余资源，并且i 为存储器的最后一层，则该裸片能使用的冗余资源为本层及前面所剩余的，则该裸片需满足的条件为：

RF<=RR*L-RS

CF<=CR*L-CS

若裸片i 不为存储器最后一层，则该裸片可使用三层冗余资源，所以只需满足条件：

RF<=RR*(i+1)-RS

CF<=CR*(i+1)-CS

同时，在其后添加排序中的最小值，并判断其是否为存储器最后一层，条件与前一层相同；重复以上一大一小的交替堆叠，直到存储器完成堆叠。需要注意的是，为了使得冗余资源与故障数相匹配，当多个S 相等时，优先选择RF 与CF 数值最为接近的裸片，或当预设冗余资源不相等时，优先选择所需冗余资源预设更为富余的冗余类型。

当一个存储器堆叠完成，即i=L 时，将相应裸片从排序中去除；若遍历完所有裸片仍无法完成堆叠，则将此次堆叠中的所需资源数之和的最大值裸片从排序中删除，并继续进行堆叠；当进行新的堆叠时，排序中所剩裸片数量小于L 时，结束堆叠。堆叠算法流程图如图2所示。

图2：堆叠算法流程图

下面通过一个堆叠存储器的例子来具体讲述堆叠的过程：

表1为通过测试与修复得到的六片裸片所需行列冗余资源数的数值表，并且已经按照资源数之和降序排列。假设存储器每个需要四层裸片完成堆叠，且每层分配2 个行冗余及2 个列冗余，则六片中没有需要直接抛弃的裸片；接着，挑选出其中的资源数和的最大值，即为A 和B 两个裸片，此时，为了满足自适应匹配原则，挑选行列冗余更加接近的B 裸片进行堆叠，再从最小值中挑选出E和F 进行匹配，匹配后发现满足条件，则前三层堆叠完成；第四层挑选出最大值裸片A 进行堆叠，发现其RF 并不满足堆叠条件，则继续进行挑选，得到裸片C，而裸片C 满足堆叠条件，并且其为存储器最后一层，则E、B、F、C 裸片堆叠成为一个存储器。

表1：堆叠示例表

2.3 算法特色

本文算法在优化存储器堆叠成品率方面主要运用了邻近层资源共享的策略，其优势在于使用了小于全局共享策略的TSV 数量，得到了略低于全局共享策略的成品率，因而大大降低了成本；同时，与结对共享相比，虽然TSV 数量增多，但成品率的提升却是显著的，并且由于邻层共享的灵活性，使得资源的利用率得到了提高。

与相同策略的文献[1]中的算法相比较，本文算法不仅优化了ESP 算法，并且在堆叠算法中提出了用所需资源较少的优质裸片去帮助堆叠所需资源较多的裸片的策略，这种策略使得在挑选裸片的过程中有了较大的弹性，一部分所需资源较多的裸片也可以被挑选进行堆叠，因而大大提升了成品率；同时，在ESP算法和堆叠算法中，本文还提出了冗余资源与故障数自适应匹配的策略，即为平衡行列冗余资源的使用，以此来提升资源使用的合理性，也一并提高了堆叠时的成品率。

3 实验结果

根据以上算法，进行了以1000 个256×256 的裸片为对象的成品率仿真实验，仿真中针对故障分布服从常用的泊松分布，并使用的是均匀故障分布的模型，计算成品率的公式为 成品率=已修复的芯片数/总芯片数 * 100%，最后取值为1000 次实验的平均值，实验结果如表2所示。

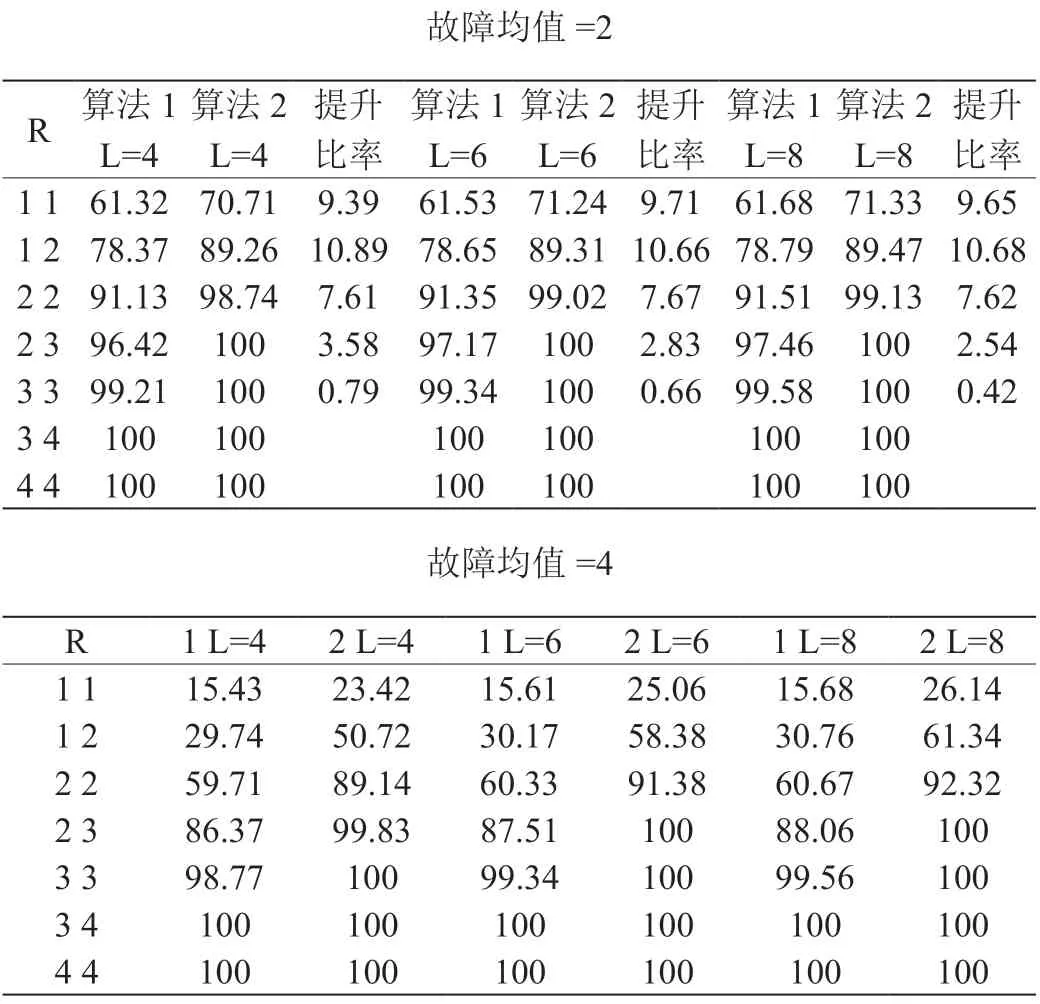
表2：实验结果表

4 实验结果讨论及分析

文献[1]的算法过程简单来说就是在得到所需行列冗余资源数后，对其和进行降序排列，并从排序中最大值开始堆叠裸片，并在之后的堆叠中，在满足条件的同时，挑选排序中的最大值来进行堆叠。从仿真结果来看，本文算法在任何情况下与文献[1]的算法相比都有着明显的提升，并且当层数越高时，差距越明显；算法的显著提升归功于其对于故障较多裸片与故障较少裸片的配对应用，使得更多的多故障裸片可以被投入使用，并且本文算法将冗余资源与所需资源数进行匹配使得成品率有了更明显的提高，而本文算法在层数上升时的巨大提升推测是因为当层数只有4 层时，第四层所能满足条件的裸片需要为所需资源数最大值且只能使用上一层与自身的资源，而当层数上升到6 层时，堆叠中可以增加一个所需资源数较少的裸片单位，而排序的底端通常都是所需冗余资源数为0 或几乎为0 的裸片，则增加的冗余较少裸片对于存储器中的资源提升是巨大的，大大增加了存储器的堆叠成品率。

当故障均值为2 时，本文算法可以在RF 为2，CF 为2 时使得成品率接近100%，而冗余资源提升对成品率的提升也极为有限，而本文算法在RF 为2，CF 为2 时的成品率接近100%，因此当使用文中的算法时，若故障均值为2，算法的最佳冗余数为RF 为2，CF 为2；当故障均值为4 时，算法在RF 为2，CF 为3 时成品率即可达到接近100%，最佳冗余数是RF 为2，CF 为3 时。

比之传统的邻近冗余资源共享，算法对裸片的匹配进行了优化，从而提升了成品率，在成品率提高的同时，其与其他如全局冗余共享或单独邻层冗余共享的优势在于，效率较高的同时大大降低了TSV 的使用面积，使得存储器的大小成本进一步降低。

5 总结

本文以邻近层冗余资源共享为基础，即存储器中的裸片不仅可以使用本层的冗余资源进行修复，同时也可以使用邻近层多余的冗余资源进行修复，提出了一种优化三维存储器堆叠成品率的方案，并且在对裸片进行修复的ESP 算法以及堆叠算法本身上进行了资源与故障数自适应匹配的处理。在堆叠算法中，通过以所需资源较少的裸片来帮助堆叠所需资源较多的裸片的方式，使得一部分本身无法进行堆叠的裸片可以进行堆叠，以此来提升堆叠成品率；而自适应匹配的处理则大大提升了资源的利用率，同时也改善了资源利用的合理性，使得成品率进一步提升。实验结果表明，与使用相同策略的文献[1]的算法相比，成品率有了显著的提高，并且堆叠的层数越高，提升越为明显。