工作压力下法兰结构螺栓及密封件受力特性
薛 杰,黄金平
(西安航天动力研究所 液体火箭发动机技术重点实验室,陕西 西安 710100)
0 引言
工程系统中有许多相互连接的管路须承受在变化范围很宽的压力和温度下的各种流体力。为防止内部流体的泄漏,管路一般设计有一个或多个法兰静密封。一旦密封不严,轻者减少产品结构寿命、降低产品性能指标,重者直接导致产品功能丧失进而引起结构破坏。因此,这种法兰连接件的设计必须做到高可靠和“零泄漏”。为了提高密封法兰的实际工作性能,喻健良等对法兰密封系统螺栓加载方式进行了试验研究,得到了以扭矩增量控制法顺次加载能获得均匀的螺栓载荷。冉振等分析了高压自紧密封式法兰的密封性能,结果表明密封环外径对法兰密封环的应力分布均匀性有显著影响,密封环外径存在一个最佳区间。程帅等研究了强脉冲载荷作用下法兰结构的螺栓预紧力设计问题,得到螺栓动态拉力随载荷峰值、脉宽的变化规律。文献[4-7]开展了法兰密封结构预紧方法及密封性能的研究,对比了包括ASME星形拧紧法在内的3种预紧方式间的差异及其影响规律。刘明提出了以弹性交互作用系数法为基础的螺栓加载载荷修正式计算方法。而在法兰密封失效及数值仿真方面,研究人员也做了许多具有实际可借鉴性的研究工作,但上述文献都没有涉及工作压力下法兰连接中螺栓力及密封件接触力变化机理的研究。特别是在一些特殊行业的工程设计中,结构件往往都是非标准件,可参考的各类标准及手册非常少,如液体火箭发动机系统,许多法兰密封设计更多的是依靠型号间的设计经验和产品试验,这种情况下明确法兰连接中螺栓力及密封件接触力变化机理就十分重要。
本文在法兰螺栓受力分析的基础上,运用理论分析的方法把工作压力下螺栓力变化及密封件接触力变化的机理用基本公式清晰地表示出来,并结合有限元分析,对理论分析结果进行了验证,得到了螺栓力、密封件接触力与关键密封参数之间的变化关系,得到了一些结论,为法兰密封的设计及结构优化提供参考。
1 法兰螺栓受力分析
典型的整体法兰结构由法兰1、法兰2、密封件(密封环)及连接螺栓组成。整体法兰结构在预紧及工作过程中的受力分析见图1。

图1 法兰密封结构受力分析
力学分析假设条件:
1)比起法兰端面内外直径,密封件内、外径差相对较小,因此均用其内半径R
表示。2)法兰肩在工作压力及螺栓力作用下绕密封件截面中点A
作刚性转动。3)螺栓、法兰及密封件的力学行为均为弹性小变形。
图中,n
为法兰连接管路内半径,N
为法兰连接管路外半径,R
为密封件内半径。另外,在整体法兰设计的国家标准中,大部分法兰的相关参数均存在以下关系:R
>N
>n
。通过结构的力学分析,得到法兰轴向方向的力增量平衡方程及螺栓法兰的变形协调方程
πR
Δp
-K
d=ΔF
(1)
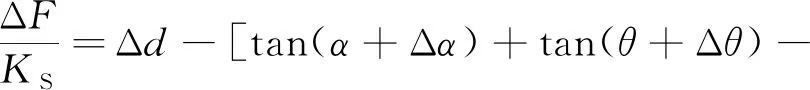
(2)
式中:Δp
为工作压力;Δd
为作用工作压力后密封件回弹量;K
为密封件的压缩/拉伸刚度;F
为总螺栓预紧力;ΔF
为作用工作压力后总螺栓力增加量;K
为总螺栓拉伸/压缩刚度;L
为螺栓轴线至密封件截面中心距离;α
、θ
分别为法兰1、法兰2在螺栓预紧状态下转动的角度(弧度);Δα
、Δθ
分别为法兰1、法兰2从螺栓预紧状态到工作压力下转动的角度(弧度)。
(3)
α
、θ
、Δα
、Δθ
为小角度情况下有tan(α
+Δα
)+tan(θ
+Δθ
)-tanα
-tanθ
≈Δα
+Δθ
因此,式(2)与式(3)合并可以写成

(4)

K
、K
分别表示法兰1、法兰2端面当量弯曲刚度。本文分析中认为两个连接法兰相同,那么,K
=K
=K
,即Δα
=Δθ
,这种情况下,从式(1)、式(4)中得到
(5)
对M
进行简单积分得到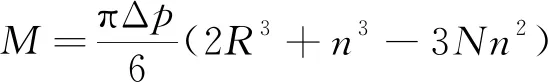
代入式(5),得到
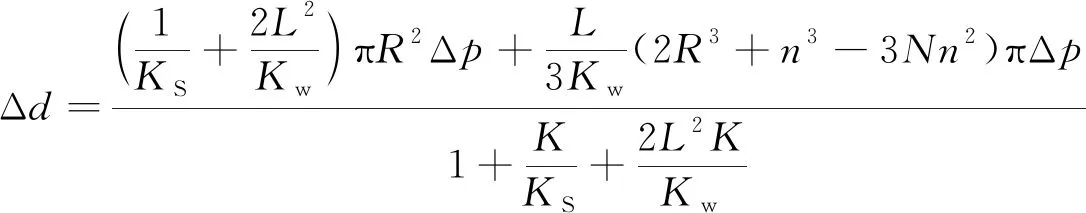
(6)
式(6)表明:密封件回弹量Δd
与工作压力成正比。以下通过三维法兰结构模型进行数值仿真验证。2 典型法兰结构仿真及理论验证
为了检验工作压力下法兰结构力学分析及理论推导的正确性,以下取某个实际法兰结构进行仿真验证。法兰结构1/32模型如图2所示,基于Abaqus软件建立的有限元模型见图3,其中法兰、螺栓及密封件等组件均采用六面体单元进行离散,各组件间采用接触关系模拟实际连接状态。各模型参数及材料力学性能参数分别如表1和表2所示。

表1 法兰连接结构各模型参数

表2 法兰接连结构材料参数
图2 法兰密封结构1/32模型
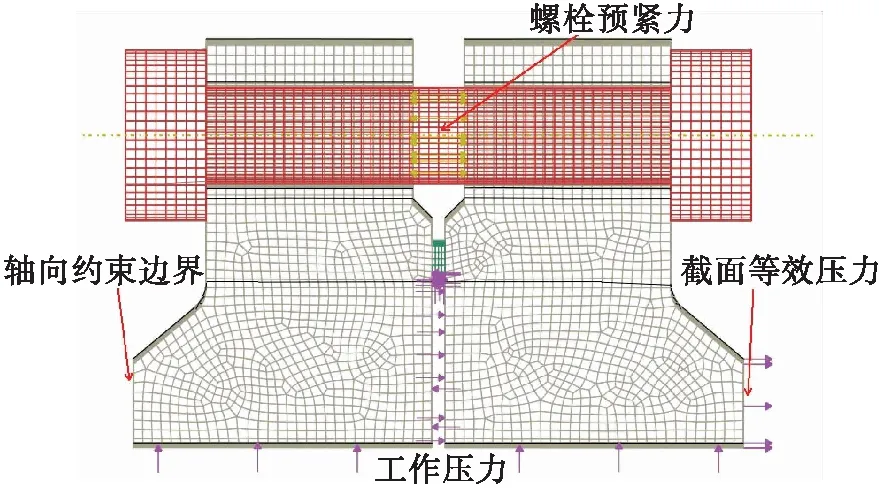
图3 法兰密封结构1/32有限元模型
计算中,截面等效压力p
计算如下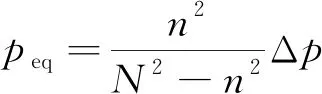
(7)
仿真分析的第一步预紧螺栓(90.6 kN),第二步施加工作压力(Δp
=4 MPa)。通过计算,得到密封件压缩量在螺栓预紧过程、实际加压过程中的变化曲线,见图4。其中,加载因子用于表征计算过程中载荷步的进程。密封件回弹量随压力变化的理论计算曲线及数值仿真曲线见图5。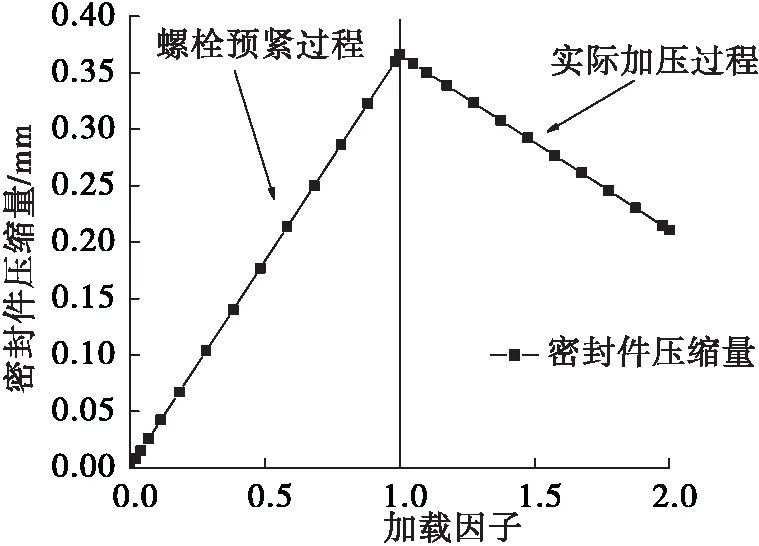
图4 密封件压缩量在螺栓预紧过程、实际加压过程中的变化曲线

图5 密封件回弹量随压力变化的理论计算曲线及数值仿真曲线
结果表明理论计算与数值仿真相差小于5%,并且均与压力载荷成正比,这说明法兰密封结构在工作压力下的受力分析及理论推导是正确合理的。
3 螺栓力密封件接触力变化分析
把式(6)代入式(1),得到工作压力下螺栓力增量公式
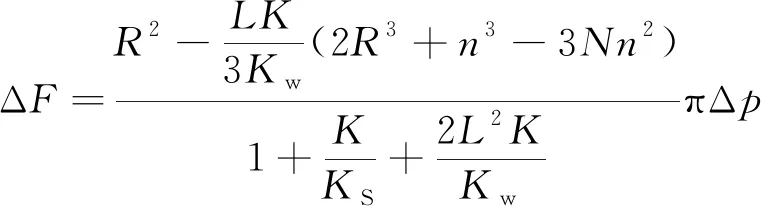
(8)




另外,还可以得到以下关系式
ΔF
<πR
Δp
(9)
这表示作用工作压力后,总螺栓力增量一定小于工作压力引起的法兰轴向分力。
针对上述实际的法兰结构,通过式(6)与式(8)并经简单换算,给出作用工作压力后总螺栓力增量ΔF
、密封件接触力减小量Δf
与密封圈内半径R
、螺栓与密封件距离L
、密封件拉伸刚度K
之间的关系,分别见图6~图8,其中,Δf
=K
Δd
。图6(a)、图7(a)分别表示工作压力作用下,总螺栓力增量随密封圈内半径R
、螺栓与密封件间距L
的增大近似地线性减小,但后者斜率更大。图8(a)表示工作压力作用下,总螺栓力增量随密封件拉伸刚度K
的增大呈降速率地减小,在高于某一临界刚度后变成负值,即螺栓力在工作过程中会有变小的情况。
图6 螺栓力增量、密封件接触力减小量随R的变化曲线
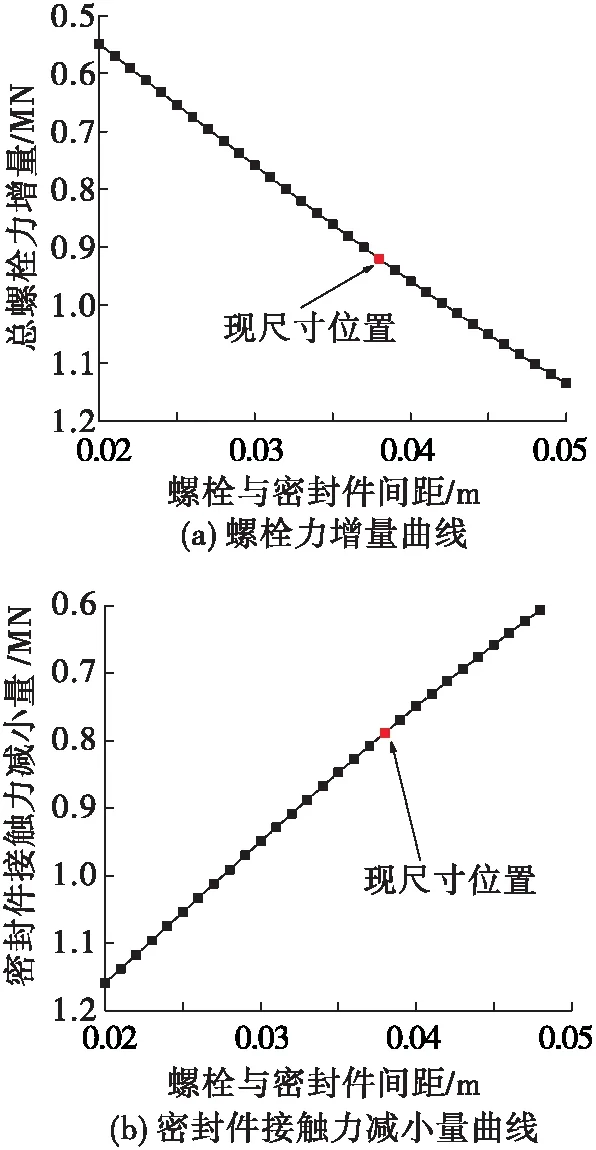
图7 螺栓力增量、密封件接触力减小量随L的变化曲线
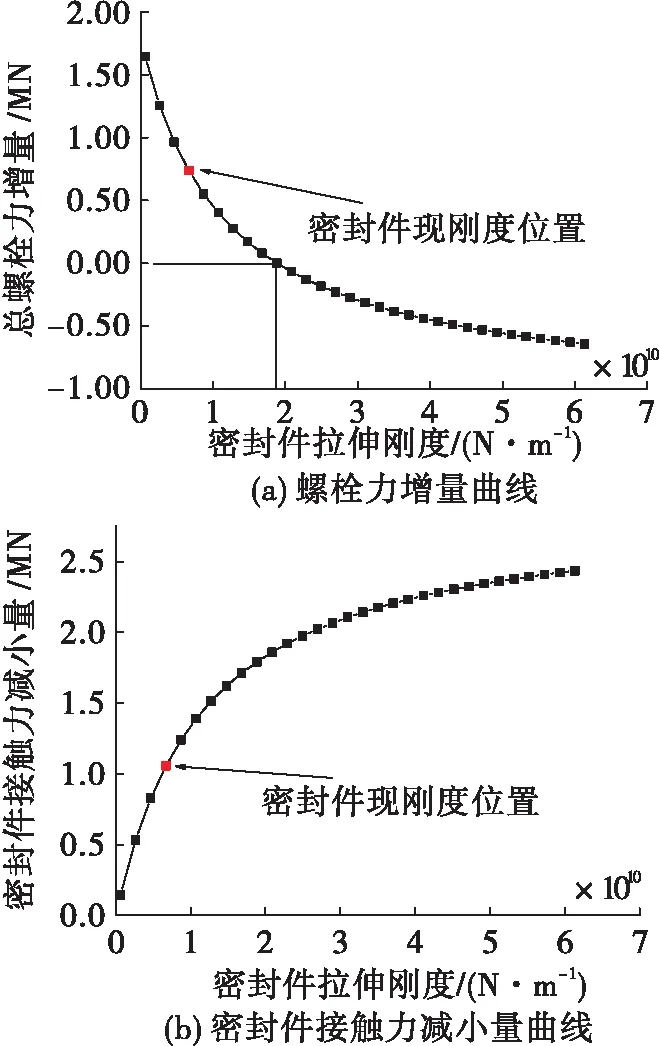
图8 螺栓力增量、密封件接触力减小量随K的变化曲线
图6(b)、图7(b)分别表示工作压力作用下,密封件接触力减小量随密封圈内半径R
、螺栓与密封件间距L
的增大近似地线性增加,但后者斜率更大。图8(b)表示工作压力作用下,密封件接触力减小量随密封件拉伸刚度K
的增大呈降速率地变大,而密封件接触力减小量过大则会导致密封性能下降甚至失效。4 结论
基于密封法兰结构的力学分析及理论计算,可以得到以下结论:
1)作用工作压力后,总螺栓力增量一定小于工作压力引起的法兰轴向分力。同时,本文所推导出的详细关系式和文献[20]的结论一致。
2)作用工作压力后,总螺栓力增量随密封件拉伸刚度的增大呈降速率地减小,在密封件拉伸刚度高于某一临界刚度后变成负值,即螺栓力在工作过程中会有变小的情况出现。
3)在密封法兰结构的设计中,减小密封圈内半径R
、螺栓与密封件间距L
的尺寸,有利于提高密封件在工作过程中的密封能力。4)本文在进行法兰结构的力学计算分析中,虽只考虑矩形截面密封环,但其方法本身适用于各种小截面形式的弹性密封件,以上结论具有一定的普遍性。

