基于数值仿真的涉河桥墩阻水效应研究

魏炜

涉河工程的建设，占用了河道的过水面积，导致水位壅高及水流流动模式的改变，给河床、河岸的稳定以及行洪带了负面影响。文章以大新县桃城农场中桥为例，采用数值仿真的方法模拟桥墩的阻水效应，分析了工程建设前后壅水和流速的变化，为评估涉河桥墩阻水效应提供参考。

数值仿真;阻水效应;桥梁;桥墩

U442.3+9A170604

0 引言

随着我国“交通强国”战略的实施，新一轮基础设施的建设热潮正在掀起，涉河工程的建设也越来越多[1]。涉河工程的建设，势必会占用河道的过水面积，产生阻水效应，导致河道范围内水流的流动模式改变、水位壅高等现象产生，进而影响河床、河岸的稳定[2]。目前对于河道阻水及流态分析大都采用经验公式或者一维水力学模型来计算分析[3]，但这些方法往往会由于河道类型不同而产生不同的结果。因此，本次研究探索采用仿真模拟的方法来计算涉河桥墩的阻水效应影响，对桥墩阻水效应的定性和定量分析具有十分重要的现实意义。

1 计算原理及方法

本次数值仿真计算的原理如下：（1）通过整合水平动量方程和连续方程得到浅水方程，据此在河道深度上集成不可压缩的雷诺Naviertokes方程;（2）通过采用单中心的有限体积法离散原始方程的空间，并将空间域由连续离散细分成非重叠的三角形非结构化网格单元[4];（3）对流通量的计算采用Riemann金斯求解，可方便处理非连续的解决方案，时间积分采用显式积分方法，详细计算原理参考文献[5]。

本次研究仿真采用的实验工具为MIKE 21FM软件，它是DHK（Danish Hydraulic Institute，丹麦水力研究所）所研发，是专门用于模拟河流、湖泊、河口、海湾、海岸以及海洋的水流、波浪、泥沙及环境的工程软件包[6]，在本研究中用于对涉河桥墩进行阻水仿真模拟计算。

2 研究对象的基本情况

本次研究对象为崇左市大新县县城内的桃城农场中桥，桥址位于向水河上游河段，坐标为东经107°10′44″，北纬22°51′04″。

2.1 桥梁工程设计方案

桃城农场中桥采用三跨预制小箱梁结构，桥梁纵轴线与河道中线处于60°斜交。综合地形因素，桥跨布置考虑为：3.5 m（桥台）+20 m+40 m+20 m+3.5 m（橋台）=87 m，单幅宽度为20 m，桥台采用承台加桩基础。桥梁设计标准按100年一遇洪水设计，相应水位为H1%=251.61 m（建前），相应流量为Q1%=860.7 m3/s。

2.2 河流水文情势

桃城农场中桥斜跨向水河。向水河又名利江，属黑水河一级支流，干流长89 km，集水面积为1 672 km2，平均坡降3.17‰，多年平均流量为29.1 m3/s。向水河宽度为30～60 m，河水深度约2～3 m，岸坡以粉质黏土为主，河床以粗砂为主，河水水流常年偏缓慢，水流对河岸及河床冲刷影响较小。

2.2.1 河流洪水频率

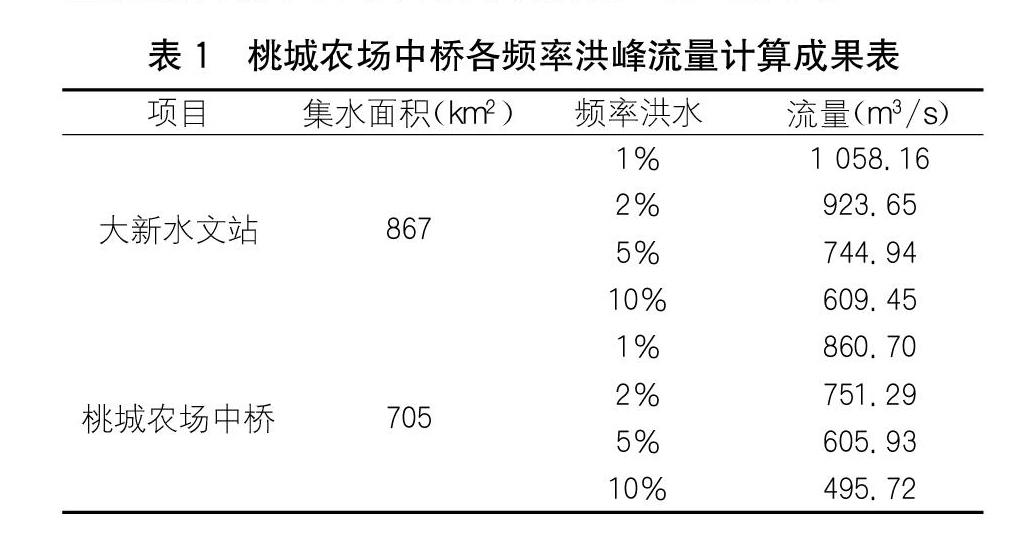
向水河上设有国家基本水文站——大新水文站。大新水文站于1958年设站，位于桃城农场中桥桥址下游3.5 km处，集水面积为867 km2。根据大新水文站1959—2015年连续57年的实测洪水资料，加入1936年历史洪水（重现期取79年），采用P-Ⅲ型曲线适线，分析计算得到大新水文站不同频率的设计洪水，再根据水文比拟法[7]按面积比的2/3次方换算至桃城农场中桥断面洪水成果，如表1所示。

2.2.2 控制断面洪水位

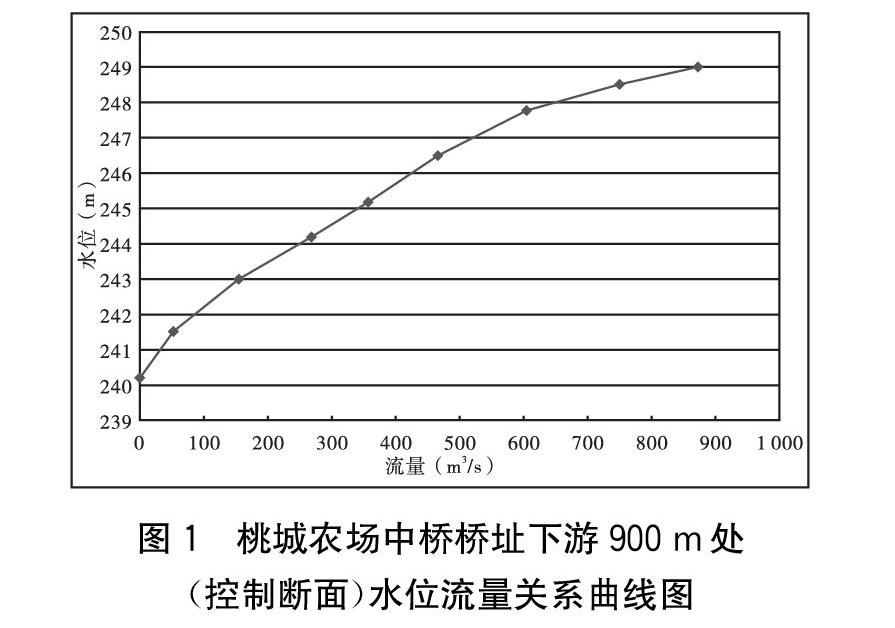
结合收集的实测资料以及计算范围情况，本次研究选择桃城农场中桥桥址下游900 m处的河道断面作为水位控制断面。根据实测的大断面资料，按恒定均匀流速进行计算，采用曼宁公式计算控制断面在不同水位情况下过水断面流量，高水部分以附近历史洪痕点作为控制点，并参照曲线的趋势延长，最终得到控制断面的水位与流量关系曲线成果，如表2和图1所示。

3 阻水效应数值仿真模拟

3.1 仿真计算方案及边界条件

为了研究桃城农场中桥桥墩对河道行洪产生的影响，本次研究拟定100年一遇洪水、20年一遇洪水、10年一遇洪水和5年一遇洪水四个频率方案，对每个方案桥梁修建前后的洪水水位、流场进行仿真模拟计算。河段水流仿真计算条件上边界采用设计洪水流量，下边界采用出口控制断面洪水位。各方案的上下游边界条件如表3所示。

根据桃城农场中桥工程所处河段的特点，选择仿真计算河道区域为桥址上下游各900 m河段水域，共计1 800 m河道长度，并建立对应河段数字化地形图（见下页图2）。为对比分析桥梁建设前后水位和流态的具体变化情况，在仿真计算水域布设一系列采样点。本次研究从上至下沿河道布置了43个断面，并在每个断面的深泓线、两岸线上分别布置了采样点，采样点布设情况如下页图3所示。

3.2 仿真结果分析

3.2.1 壅水仿真分析

利用Mike 21FM水动力模型对各方案进行仿真计算分析，并根据采样点水位差值绘制不同频率下纵向差值曲线图，左岸线、中泓线、右岸线水位差值曲线图如下页图4所示。

根据图4分析可得，在100年一遇洪水情况下，桥梁建设后水位最大壅水量为0.093 m，在桥梁上游35 m左岸线处;在50年一遇洪水情况下，桥梁建设后水位最大壅水量为0.117 m，在桥址左岸线处;在20年一遇洪水情况下，桥梁建设后水位最大壅水量为0.116 m，在桥址左岸线处;在10年一遇洪水情况下，桥梁建设后水位最大壅水量为0.200 m，在桥址左岸线处。由此可见，桥梁工程的建设对大频率洪水情况下壅水影响较大，说明向水河属于山谷型河流。所有的洪水频率下，桥梁壅水的最大值都出现在左岸线上，说明桥梁的建设对左岸线的阻水效应更明显。

对图4进行对比分析可知，10年一遇的洪水整体比其他频率的洪水情况下阻水效应大，洪水越大时，桃城农场中桥的阻水效应越小。桃城农场中桥下游100 m后阻水效应很小，几乎不受桥梁工程建设的影响，但在上游900 m仿真范围内都受桥梁工程建设的影响。

3.2.2 流速仿真分析

根据采样点流速差值绘制不同频率下纵向流速差值曲线图，河道左岸线、中泓线、右岸线流速差值曲线图如图5所示。

根据图5分析可得，在100年一遇洪水情况下，桥梁建设后流速变化最大在桥址下游30 m右岸线处，减缓为0.13 m/s;在50年一遇洪水情况下，桥梁建设后流速变化最大在桥址中泓线处，减缓为0.21 m/s;在20年一遇洪水情况下，桥梁建设后流速变化最大在桥址右岸线处，减缓为0.24 m/s;在10年一遇洪水情况下，桥梁建设后流速变化最大在桥址中泓线处，减缓为0.19 m/s。对比仿真采样结果可知，有三个方案的桥梁建设后流速变化最大量都发生在桥址断面，说明在桥址断面水流流速变化复杂，但是整体是显示减小的趋势。

结合图5分析可知，10年一遇的洪水整体比其他频率的洪水情况下流速变化较大，减缓量也较大，这跟其壅水效应相一致。洪水越大时，桃城农场中桥的建设对流速变化影响就越小。桃城农场中桥下游200 m后流速变化很小，几乎不受桥梁工程建设的影响，但在上游900 m仿真范围内由于壅水抬升，桥梁建设后流速整体都放缓。

4 结语

（1）对于山谷河流，洪水越大，桥梁建设对河道行洪壅水效应越小，对流速变化的影响越小。

（2）桥梁工程建设后，桥梁上游区域会形成一定的壅水，河流流速会减缓，桥梁下游附近区域会降水，但由于桥梁阻水消能后也会导致水流流速减缓。

（3）本次研究对象桃城农场中桥工程建设后，在防洪标准100年一遇洪水范围之内，最大壅水量为0.200 m，流速最大变化量为0.24 m/s，对河道的阻水效应整体较小。

[1]張维锋，兰懿凡.宿迁上海路工程跨河桥梁跨径研究[J].城市道桥与防洪，2020（8）：150-152，17.

[2]宋 涛.某跨河桥梁工程防洪评价分析[D].邯郸：河北工程大学，2018.

[3]王春宇.基于二维水动力学模型的河流水力学特征分布研究[J].水利技术监督，2016，24（4）：56-58，101.

[4]任叙合，何 帅，李保石.茅尾海生态修复工程对冲淤影响的数值模拟研究[J].海洋湖沼通报，2016（6）：20-28.

[5]魏 炜，谢 军，刘 芳.MIKE 21FM二维水流计算模型在桥梁防洪评价壅水计算中的应用[J].西部交通科技，2018（12）：76-81，180.

[6]陈宏景.福州市左海-西湖水体水质提升方案[J].净水技术，2019，38（11）：18-21.

[7]虞 慧，李友辉，孔琼菊，等.新安江模型在白云山水库日径流模拟的应用[J].江西水利科技，2017，43（4）：293-296.