厚尾噪声条件下星凸形扩展目标student’s t滤波器

陈 辉, 张星星, 杨文瑜

(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 中国民航大学 电子信息与自动化学院， 天津 300300)

传统目标跟踪算法主要以点目标(小目标)假设为前提,然而,由于高分辨率的现代传感器出现以及对跟踪近距离目标的需求,目标往往对应了传感器的多个分辨单元,这表现为目标在每个采样周期内产生多个量测,这样的目标定义为扩展目标(extended target,ET),其对应的跟踪问题称为扩展目标跟踪(ET tracking,ETT)[1-3].此时,简单的将目标建模为点目标不再适用于现代目标跟踪任务,目标在空间上的扩展应该表现为更为复杂的建模形式.ETT问题的提出具有非常重要的研究意义,尤其在近几年吸引了国内外学者的广泛关注.结合ET的多个量测源,通过最优滤波估计能够得到目标更为丰富的状态信息.

实际上,对ET形状估计的研究在近几年已经取得了许多引人瞩目的成果[4-6].其中,绝大多数算法利用简单几何形状(如椭圆、矩形等)来描述扩展目标的范围.典型的代表有随机矩阵模型(random matrix model,RMM)[7-8].然而这种方法仅能大致估计出目标的形状,建模对象也具有局限性.所以,在RMM的基础上,兰剑等[9]提出的用多个子椭圆来逼近一个整体不规则形状方法,利用多个子椭圆逼近非椭圆(不规则)扩展目标的形状.另一种方法是随机超曲面模型(random hypersurface model,RHM )[10-12].RHM灵活地利用傅里叶级数展开的方式对描述星凸形扩展目标的径向函数进行了参数化,通过目标形状边界的缩放利用曲线拟合的思想估计目标形状.这种方法对解决目标的识别、检测以及跟踪问题具有巨大的实际价值.

扩展目标的跟踪研究通常在假设过程噪声和量测噪声都服从高斯分布的前提下进行.但是在实际跟踪场景中,理想的高斯噪声比较少见.相较而言,厚尾噪声更接近于现实应用中有干扰的噪声,如一旦接受量测信息的传感器不灵敏或者传感器在跟踪敏捷目标的过程中遭受电磁干扰,量测噪声中很容易出现野值从而表现出厚尾特性；或者当目标在杂波环境中有大幅度机动时,由于运动模型的不准确,过程噪声中包含野值,产生厚尾过程噪声.此时再用高斯假设下的滤波器会使得滤波精度大大下降.已有文献进行了在厚尾噪声假设下利用student’s t滤波器解决目标跟踪问题的一系列研究[13-18],但仅仅限于点目标跟踪,没有考虑到ETT问题的求解.所以,思考一种在厚尾噪声分布条件下,针对ET多个量测源稳健地估计出目标的运动状态和形状轮廓的滤波算法,具有非常重要的研究意义.

本文针对厚尾过程噪声和量测噪声的环境下任意不规则形状扩展目标的跟踪问题,首先将厚尾过程噪声和量测噪声建模为student’s t分布,利用星凸形RHM对扩展目标的量测源进行建模,然后将RHM建模的空间量测分布模型与鲁棒student’s t滤波算法相结合对RHM的非线性伪量测方程进行求解.最后,通过实验仿真验证了本文算法的正确性和有效性.

1 鲁棒student’s t滤波器

将非线性离散随机系统利用状态空间模型建模为

(1)

其中:xk∈Rn表示k时刻的系统状态向量,n为系统状态维度；zk∈Rm表示k时刻的量测向量,m为量测维度；fk-1(·)和hk(·)分别为非线性系统转移函数和观测函数；wk和vk分别为系统的过程噪声和量测噪声.

由图1可以看出,与高斯分布相比student’s t分布具有厚尾特性,对野值有良好的包容度,由此student’s t分布[14]适用于对厚尾噪声建模：

(2)

将系统的初始状态向量x0建模为student’s t分布:

(3)

其中,假设x0、wk、vk互不相关.Student’s t分布和高斯分布比较图如图1所示.

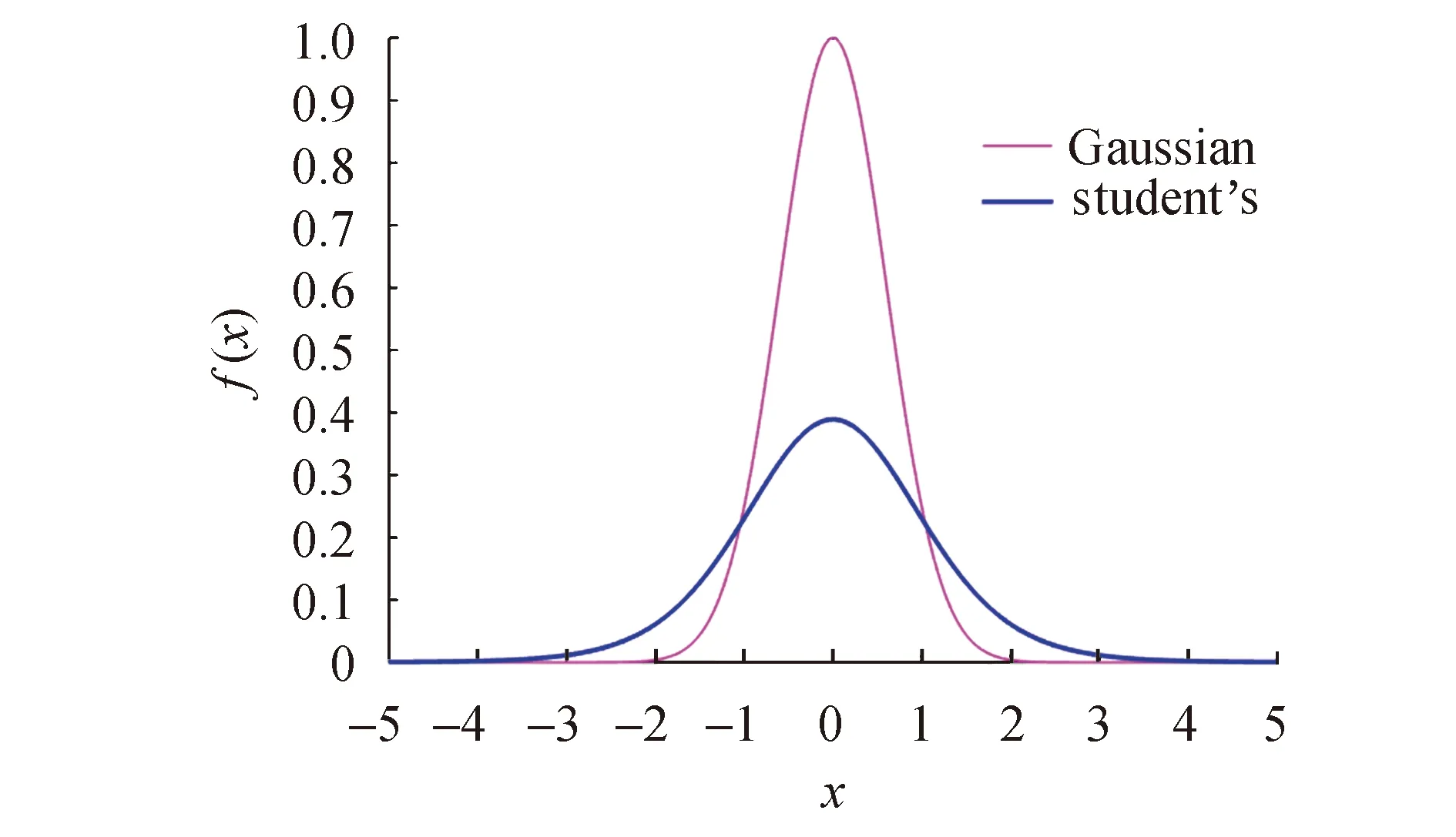
图1 高斯分布和student’s t分布Fig.1 Gaussian distribution and student’s t distribution

鲁棒student’s t滤波器的主要思想是利用student’s t分布来逼近系统的后验概率分布,即

(4)

根据文献[16],利用student’s t分布逼近系统的后验PDF必须满足以下前提条件：

假设1：系统状态和量测的联合分布为student’s t分布：

(7)

根据式(5,6),其中的各个分量为

(8)

(9)

(10)

(11)

(12)

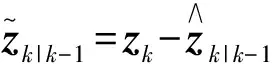
假设2：系统当前状态和系统预测状态的联合分布为student’s t分布:

(13)

其中:

(14)

根据贝叶斯滤波框架,系统的预测PDF为

(15)

很明显,由于非线性函数fk-1(·)的存在,使得预测PDF不可能是student’s t分布,所以需要在假设1的基础上将其近似为student’s t分布：

(16)

根据假设1可得参数为

同理,量测似然PDF也近似为student’s t分布：

(19)

根据假设2可得参数为

同理,将联合PDFp(xk,zk|Zk-1)近似为student’s t分布可得：

(22)

最后,利用student’s t分布近似后验分布,再根据贝叶斯理论可得：

(23)

其中：

nz表示系统的量测维度.式(16～28)构成了完整的鲁棒student’s t滤波算法,很明显在递推过程中含有大量非线性student’s t的高维积分,其求解极为困难.

2 星凸形扩展目标student’s t滤波器

不同于点目标跟踪,扩展目标跟踪不仅要估计目标的运动状态,还要估计目标的扩展形状.由此,在厚尾过程噪声和量测噪声的场景中,星凸形扩展目标student’s t滤波器首先利用星凸形RHM对目标量测源进行建模,进而估计出目标形状.然后通过鲁棒student’s t滤波器进行目标运动的估计,最后再结合三阶球面-径向容积规则[17]求解RHM的非线性伪量测方程(含非线性student’s t的高维积分).为了估计星凸形扩展目标的状态,建立如下系统的联合估计模型.

1) 目标运动模型

扩展目标在k时刻的状态表示为

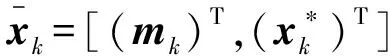
xk+1=Fxk+wk,wk～st(wk;0,Qk,v1)

(29)

2) 目标量测模型

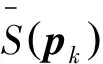
(30)

再结合径向函数r(pk,φk),S(pk)可以参数化表示为

S(pk)=sk,l·r(pk,φk)·η(φ)+mk

(31)

其中:φk∈[0,2π];r(pk,φk)表示质心和目标边界间的距离关于角度φk的函数;方向向量为η(φk)=[cos(φk),sin(φk)]T.

径向函数r(pk,φk)的有限阶傅里叶级数展开为

(32)

其中形状参数向量为

所以,径向函数为

r(pk,φk)=R(φk)·pk

(35)

由此RHM星凸形扩展目标的量测源可以建模为

yk,l=sk,l·R(φk)·pk·η(φk)+mk

因为量测模型包括传感器噪声模型和量测源模型两部分,即

zk=yk,l+vk

所以基于RHM的星凸形扩展目标的量测方程为

zk=sk,l·R(φk)·pk·η(φk)+mk+vk

(36)

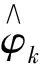
h*(xk,vk,sk,l,zk)将状态向量xk、收缩因子sk,l、量测zk和量测噪声vk映射到伪量测0,则称为伪量测方程.以上公式(29,37,38)构成了伪星凸形扩展目标跟踪的状态空间模型.在此基础上,结合鲁棒student’s t滤波器推导滤波算法.

(1) 预测部分

由于目标运动模型是线性的,在厚尾噪声下,系统的一步预测PDF如式(16)所示,根据文献[18]推导可得：

(2) 更新部分

结合以上推导得到的星凸形扩展目标的非线性RHM伪量测函数和式(20～28)所示鲁棒student’s t滤波算法的更新步,再通过采用高滤波精度的三阶球面-径向容积规则近似求解过程中出现的非线性student’s t的高维积分,得到星凸形扩展目标student’s t滤波器的更新部分.具体步骤如下：

步骤1:基于标准student’s t分布密度积分准则确定容积采样点ξi及其权值ωi为

(41)

其中:nx为系统的状态维数;ej为单位矩阵的第j列;容积点总数为2nx.

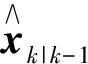
(42)

其中Sk|k-1由Pk|k-1进行Cholesky分解得到.

步骤3: 经过RHM伪量测方程传递后的容积点：

(43)

步骤4: 由经过伪量测方程传递后的容积点确定量测的预测均值、协方差为

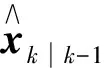
在上述滤波算法中,由式(26)可以看出随着滤波递推,自由度参数会越来越大,使得系统的厚尾特性消失.为了保持系统厚尾特性的鲁棒性,采用二阶矩匹配的方法对后验分布进行修正[18]：

(47)

在以上星凸形扩展目标student’s t滤波器算法的推导过程中,由于针对厚尾噪声选择高匹配度student’s t分布建模噪声，再用鲁棒student’s t滤波器进行系统滤波.理论上通过建模的稳定性确保了算法的鲁棒性.

3 仿真分析

本文引入一种拟Jaccard(quasi-Jaccard)距离[9]作为不规则扩展(群)目标形状估计[19-20]评价指标,k时刻扩展目标的真实轮廓与估计轮廓间的拟Jaccard距离定义为

(48)

通过构造不同情况下不规则形状扩展目标跟踪的仿真场景,在过程噪声和量测噪声均具有厚尾特性的情况下,设置用经典的UKF对星凸形扩展目标滤波作为对比算法,分别用本文所提出的student’s t滤波算法和对比算法跟踪不同形状的扩展目标、形状渐变的扩展目标以及群目标,验证所提算法对扩展目标跟踪的有效性.目标运动模型选CV模型,仿真场景设置采样周期T=1,k时刻目标的状态转移方程可由式(29)描述,其中

其中:过程噪声标准差为σw=1.5 m/s2;nf为傅里叶级数,取11;Inf为nf阶单位矩阵;尺度因子设置为s～N(0.5,0.02).目标的初始运动状态为x0=[5,10,10,5],自由度参数为v1=v2=v3=3.

厚尾过程噪声和量测噪声分别设置为

其中:R=rI2，r=100,95%的vk和wk来自于协方差为Q或R的高斯噪声,只有5%的过程噪声和5%的量测噪声来自于协方差严重增加的高斯分布.

图2和图3分别是两种算法对五角星目标的跟踪效果图和其对应的拟Jaccard距离,运动终止时刻tf=5 s,绿色的质心和轮廓为本文所提算法的估计结果，红色的质心和轮廓为对比算法的估计结果.可以看出：

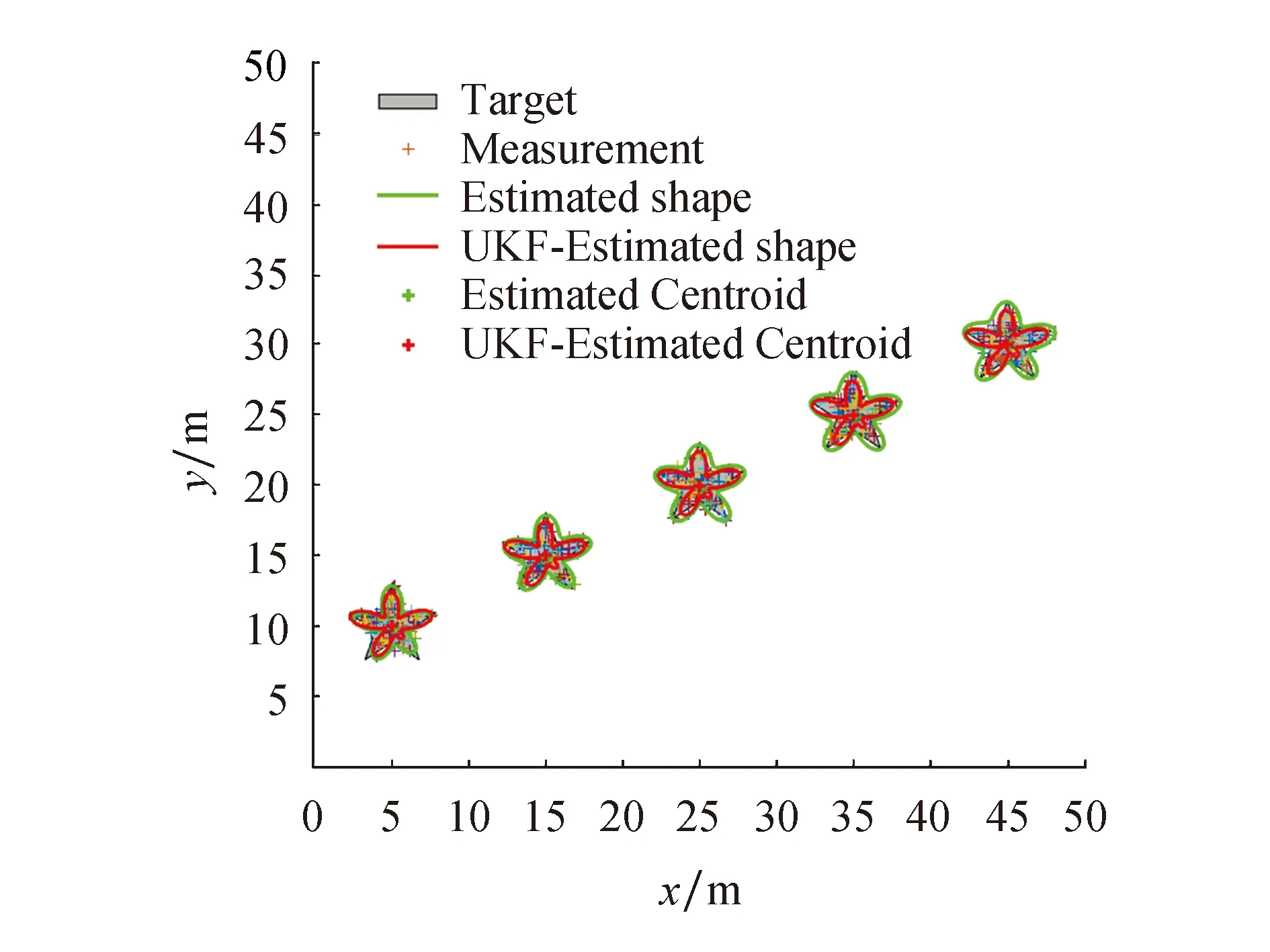
图2 五角星目标跟踪Fig.2 Pentagram target tracking

1) 随着目标的运动,两种算法都能较为准确地估计出当前时刻的目标质心位置,且估计质心基本重合.这表明两种算法都能较为准确地估计出扩展目标的运动状态.

2) 由于目标的形状先验是未知的,两种算法在初始时刻的目标轮廓估计较为粗略.但是,随着滤波次数的递推,到最终时刻只有星凸形student’s t滤波器能较为准确地估计出该五角星目标的轮廓,而另一种对比算法不能完整地估计出五角星目标的形状轮廓.

图3的拟Jaccard距离图更进一步说明了本文

图3 五角星目标跟踪拟Jaccard距离

所提算法对目标形状的估计确实比已有的算法精确.由此验证了本文所提滤波器在厚尾噪声下对不规则扩展目标的运动状态和形状都具有收敛性.

图4和图5为形状突变的扩展目标跟踪效果图及其局部放大图,运动终止时刻为tf=15 s,在第5个时刻目标形状发生突变(前4个时刻目标形状为十字架,后11个时刻目标形状为五角星).由图4可知,该滤波器能够较为精确地跟踪不规则扩展目标.图5选取了目标形状突变时刻和最终时刻的目标跟踪局部放大图.由图5a可以看出,由于大量的先验信息来自于突变前的目标,在突变刚发生时形状估计效果很差.但是,由图5b可知随着突变后滤波次数的递推,对突变后的形状仍然能达到较为精确的估计.从而验证了在厚尾噪声的环境中,星凸形student’s t滤波器对形状突变的扩展目标的不规则形状和运动状态具有收敛性.

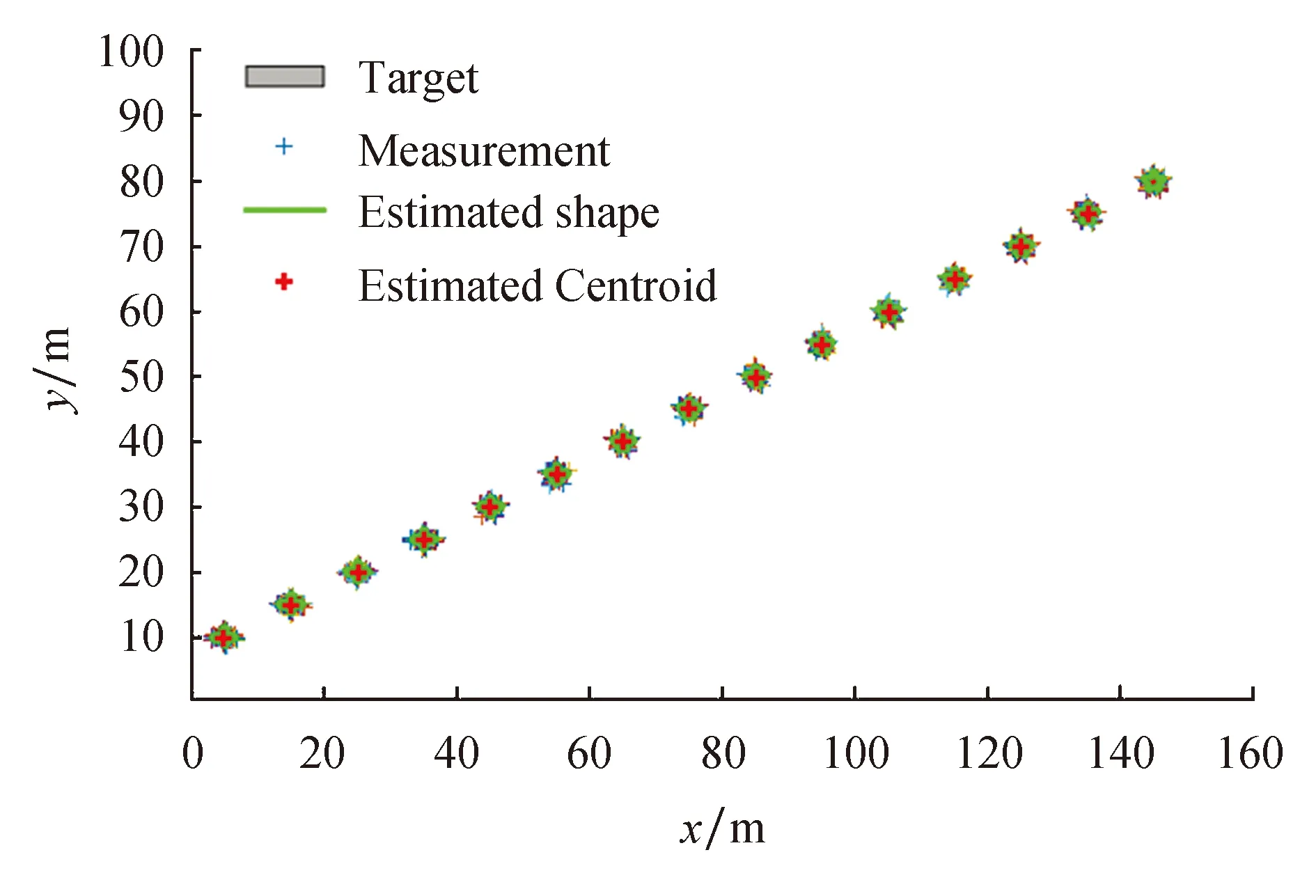
图4 形状突变目标跟踪Fig.4 Shape change target tracking

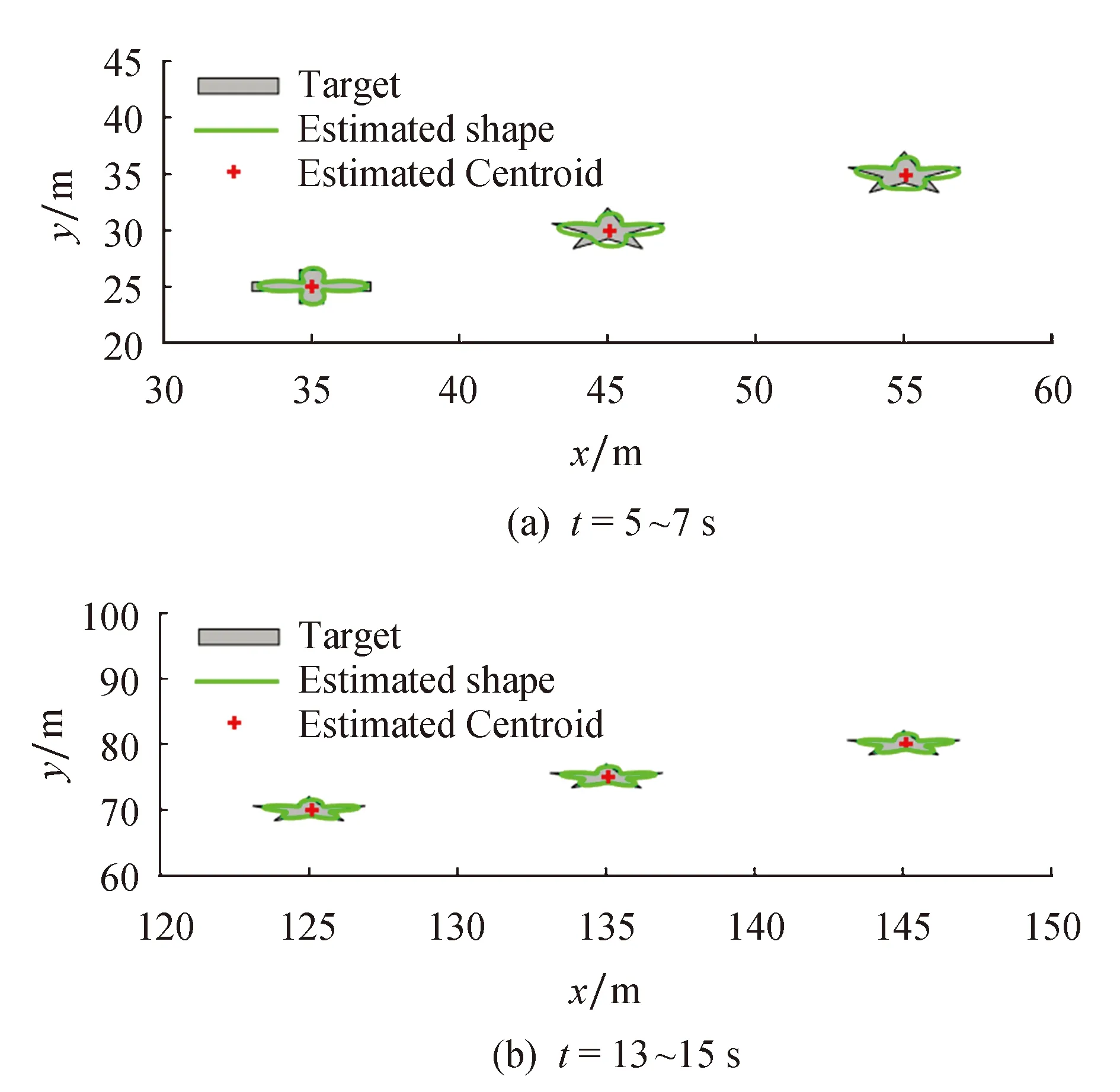
图5 形状突变目标跟踪局部放大图

图6和图7构造两种不同算法下具有形状突变的群目标跟踪实验,每个群目标由20个点目标构成.图6为群目标跟踪的形状拟Jaccard距离,图7是目标在发生形状突变时刻和跟踪的最终时刻的局部放大图,从而比较对于群目标这两种滤波器的跟踪性能.很明显,由图7a可以看出,在刚发生突变后两种算法的目标形状估计都较差,但是随着滤波次数的增加,到滤波的最终时刻如图7b所示,星凸形student’s t滤波算法估计的蓝色轮廓线与群目标的真实轮廓很接近，而对比算法估计的黑色轮廓线明显不够精确.由此可见,本文所提滤波器能够较为精确地估计出群目标此时的形状.

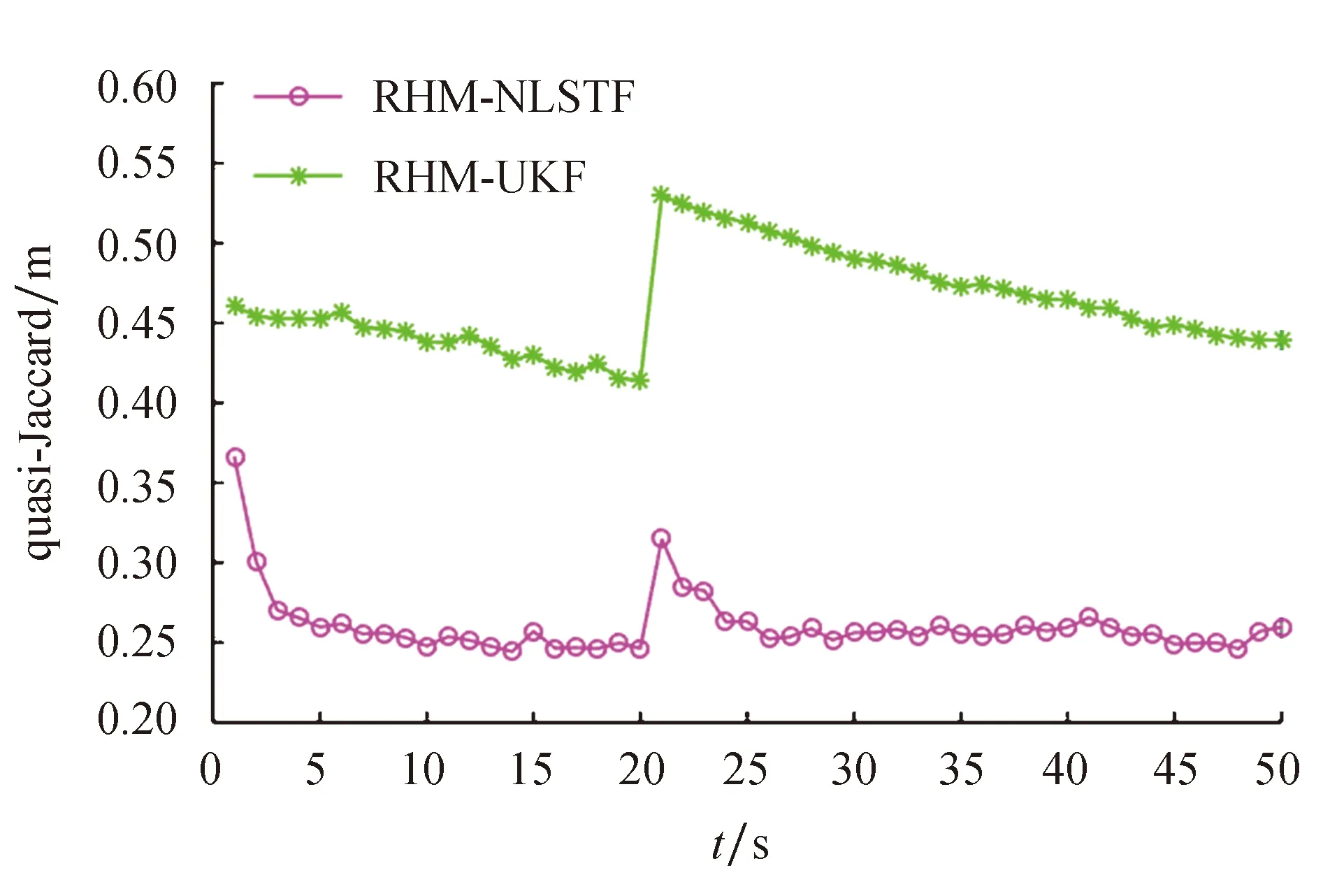
图6 群目标跟踪拟Jaccard距离Fig.6 Quasi-Jaccard distance statistics of the group target tracking

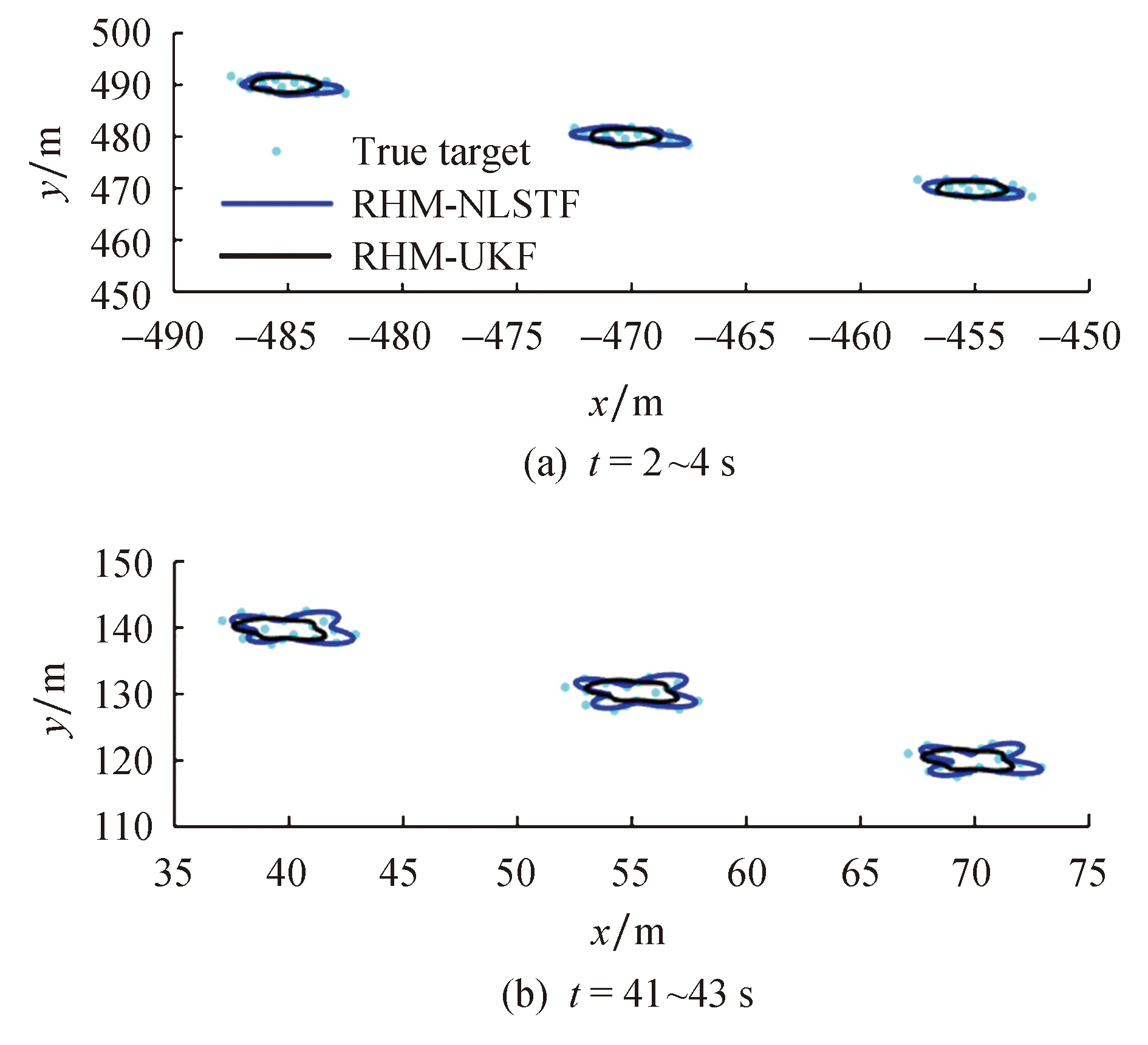
图7 群目标跟踪局部放大图Fig.7 Partial enlarged detail of the group target tracking

对群目标跟踪实验,在同样的厚尾噪声设置下进行了100次蒙特卡罗仿真,得到了图6所示的目标形状拟Jaccard距离,注意到在t=21 s时两种算法的拟Jaccard距离都骤然增加,这是由于此时群目标的形状发生突变(由四边形变为十字架)引起的,但在之后的时刻随着滤波次数的递推再次稳定.由拟Jaccard距离的比较可以明显看出,在厚尾噪声条件下相对于传统的不敏卡尔曼滤波器解决星凸形扩展目标跟踪,本文所提算法的准确性有明显的提高.

综合上述实验,本文所提出的算法在厚尾过程噪声和量测噪声的情况下,对不规则扩展目标(包括形状突变)的运动状态和形状估计都较为精确.同时对形状突变的群扩展目标(与现实意义中的编队飞行目标相似)也具有收敛性.

4 结论

本文针对非线性非高斯厚尾噪声条件下的不规则形状的扩展目标跟踪问题,提出了基于随机超曲面模型的星凸形扩展目标student’s t滤波算法.结合扩展目标形状评价指标拟Jaccard距离,在杂波环境下分别对不同形状的扩展(群)目标进行了估计状态,从而验证了所提出方法的正确性和有效性.根据仿真结果可知,本文算法可以同时较为精确地估计厚尾噪声下的扩展目标的运动状态和形状,并能较为准确地识别和跟踪群目标形状.将来的工作重点是进一步研究厚尾噪声下基于RHM的星凸形扩展目标的收敛条件及其理论证明和厚尾噪声下多扩展目标的跟踪算法.