风力机叶片等效悬臂梁模糊PID控制①

张志强, 乔印虎

(1.安徽工程大学机械工程学院,安徽 芜湖241000;2.安徽科技学院机械工程学院 安徽 凤阳233100)

0 引 言

压电材料作为一种新型智能材料,能够实现机电转换,目前在航空航天、船舶、机器人等领域具有广泛应用,20世纪以来随着新能源产业的迅速发展,在风力机上使用压电材料已经成为一种趋势。Jason Laks(2011)等[1]用光纤作为传感器对风况进行检测,实现叶片振动预控制,Hakim Boudaoud[2]对带有压电和粘弹性层的复合结构进行了有限元分析并开展主动控制研究。John Arrigan[3]针对风力机叶片的襟翼振动,提出采用半主动调谐质量阻尼器进行控制。张明明(2018)等[4]研发了安装有柔性尾缘襟翼的“智能桨叶”的整体风力机气动伺服弹性仿真平台,按方位角不同特性区域对襟翼有针对性地进行控制,进而减小作动器损耗,提高作动器控制效率和使用寿命,最终达到风机叶片降载延寿效果。乔印虎[5]等对复合材料风力机叶片采用压电板壳进行建模分析,基于压电驱动风力机叶片悬臂梁动力学模型[9],

针对能量集中的一阶、二阶模态进行控制,采用模糊PID算法对复合材料风力机叶片的振动进行主动控制。并对系统进行仿真模拟,结果表明使用模糊PID控制算法对风力机叶片振动抑制比传统PID控制有更好的效果。

1 系统模型

采用压电复合材料的风力机叶片振动能量主要集中在一阶、二阶,振动形式以挥舞为主。将压电材料嵌入到两层玻璃钢中间可等效为悬臂梁。悬臂梁运动状态由挠度描述,振动偏微

分方程为[6]:

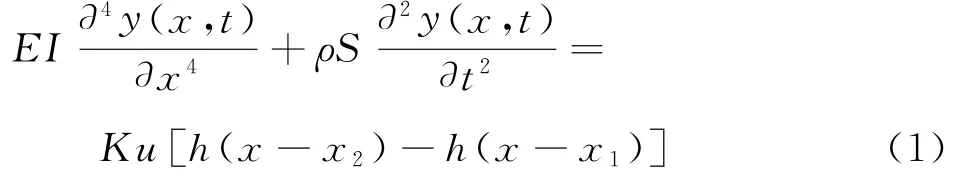
其中:F(x,t)=Ku[h(x-x2)-h(x-x1)]为压电驱动器作用下悬臂梁受到的力矩h(x)为阶跃函数(当x＞0时,h(x)=1;x＜0时,h(x)=1)[9],u为控制驱动电压。K为比例常数,表达为,因压电片嵌入风力机叶片内部,取(t p+t b)为t b。

压电传感器两表面电极间电压为:

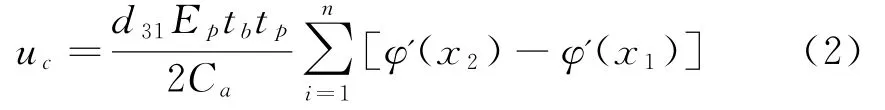
其中φ(x)为模态坐标,与挠度间转换关系为:

取状态向量

可以得到等效为悬臂梁的风力机叶片动力学状态空间表达式为:

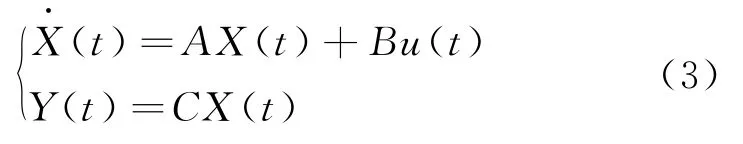
其中:Y(t)为逆压电效应下系统输出电压,A、B、C分别为系统的状态矩阵、控制矩阵、输出矩阵,计算公式如下:

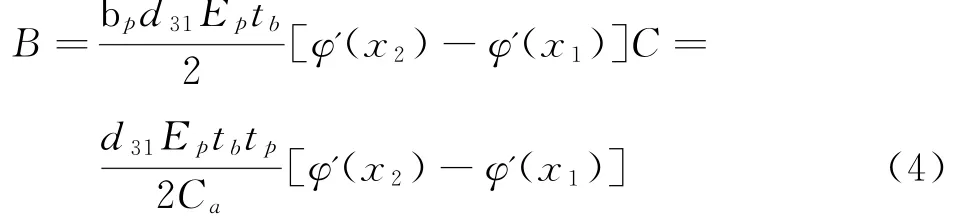
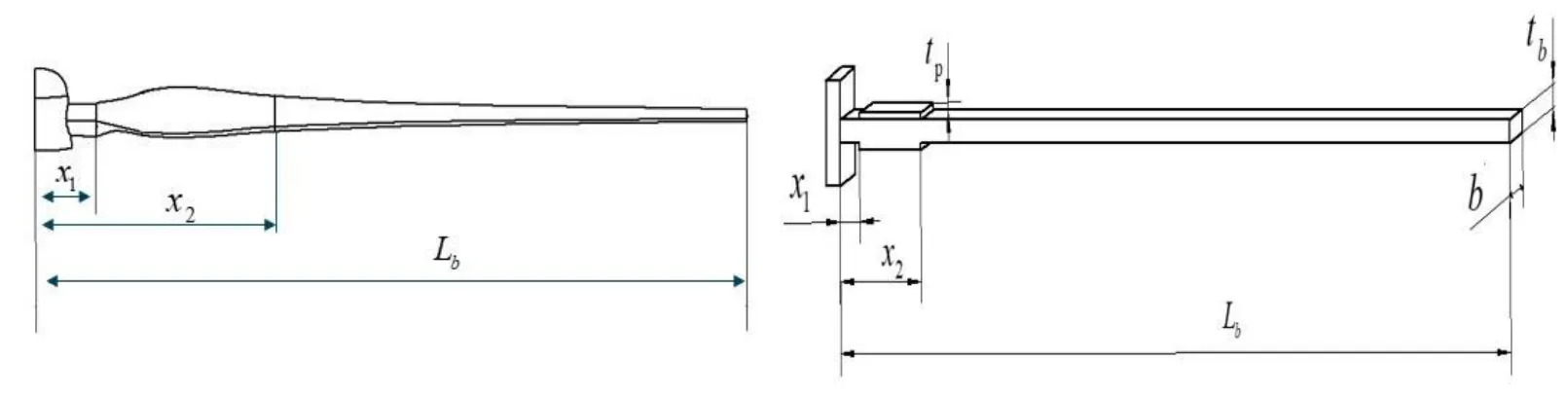
图1 等效悬臂梁尺寸参数

状态空间矩阵具体形式为:

其中:

2 模糊PID算法

2.1 经典PID算法

PID控制算法由于工作稳定,目前在工业中得到广泛使用,其由比例、积分、微分三项共同构成,根据系统输出与给定值之间的误差,实现反馈控制。为实现风力机叶片低阶模态下振动抑制,引入PID控制器,将叶片震颤幅值作为误差,经比例、积分、微分环节作用在被控对象上,达到输出幅值衰减目的。

2.2 模糊PID自整定算法

模糊PID参数自整定算法,通过e和ec之间的模糊关系,找出分别对Kp、Ki、Kd进行推理,根据模糊控制原理对三个参数在线进行修改,实现对系统的自适应控制,提高系统的动、静态性能。常用隶属函数类型有三角隶属函数,高斯隶属函数,钟型隶属函数。误差隶属函数采用三角隶属函数。

模糊控制器输入分别为振动幅值误差e和变化率ec,控制输出为Kp、Kd参数,将输入输出语言变量划分为{P,Z,N}三级模糊集合。针对风力机叶片控制系统Kp整定规则为:当振动幅值误差较大时,ΔKp取正,增大Kp。误差在零附近时分为三种情况:ec为N,ΔKp取负,ec为Z,ΔKp取正,ec为P,ΔKp取正。Kd整定规则为:误差在零附近时,ΔKd取正,否则ΔKd取零。

3 仿真分析

3.1 经典PID控制

为方便与自整定PID控制形成对比,采用普通PID作为参照,采用Simulink软件对风力机叶片等效模型进行理论仿真分析。在悬臂梁上表面粘贴压电陶瓷以逆压电效应进行驱动,压电陶瓷位于距悬臂梁根部2mm处,宽度设置与悬臂梁相等,通过Simulink仿真分析不同控制方法对悬臂梁抑制效果。假设悬臂梁阻尼为比例阻尼,取ζi=0.01。取初始扰动q1(0)=q2(0)=0.01m,q·1(0)=q·2(0)=0m,仿真参数如表1、2所示:

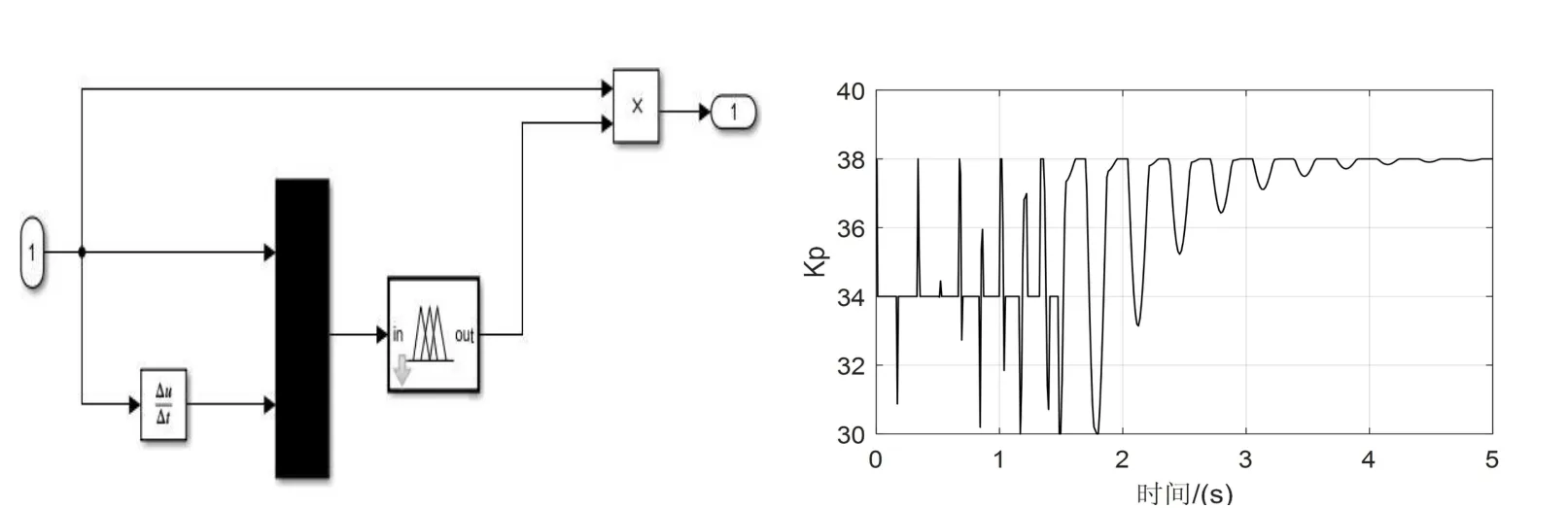
图4 Kp自整定仿真

表1 悬臂梁性能参数

表2 压电片性能参数

如图2、图3分别为采用经典PID控制时系统一阶、二阶振动响应曲线。其中一阶响应Kp=30,Ki=10,Kd=2,二阶响应Kp=10,Ki=0,Kd=5,由图2可知未施加控制时系统一阶振动响应曲线收敛速度较慢,采用PID控制不仅能够降低振动幅值而且能够提高系统收敛速度,一阶振动于4.5s后趋于稳定,由图3可知未施加控制时系统二阶振动约4s趋于稳定,使用PID控制后系统1.5s达到稳定且振动幅值缩减约50%。

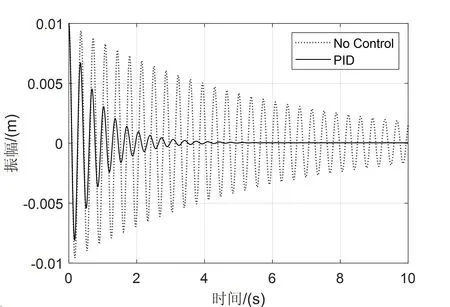
图2 一阶振动响应曲线

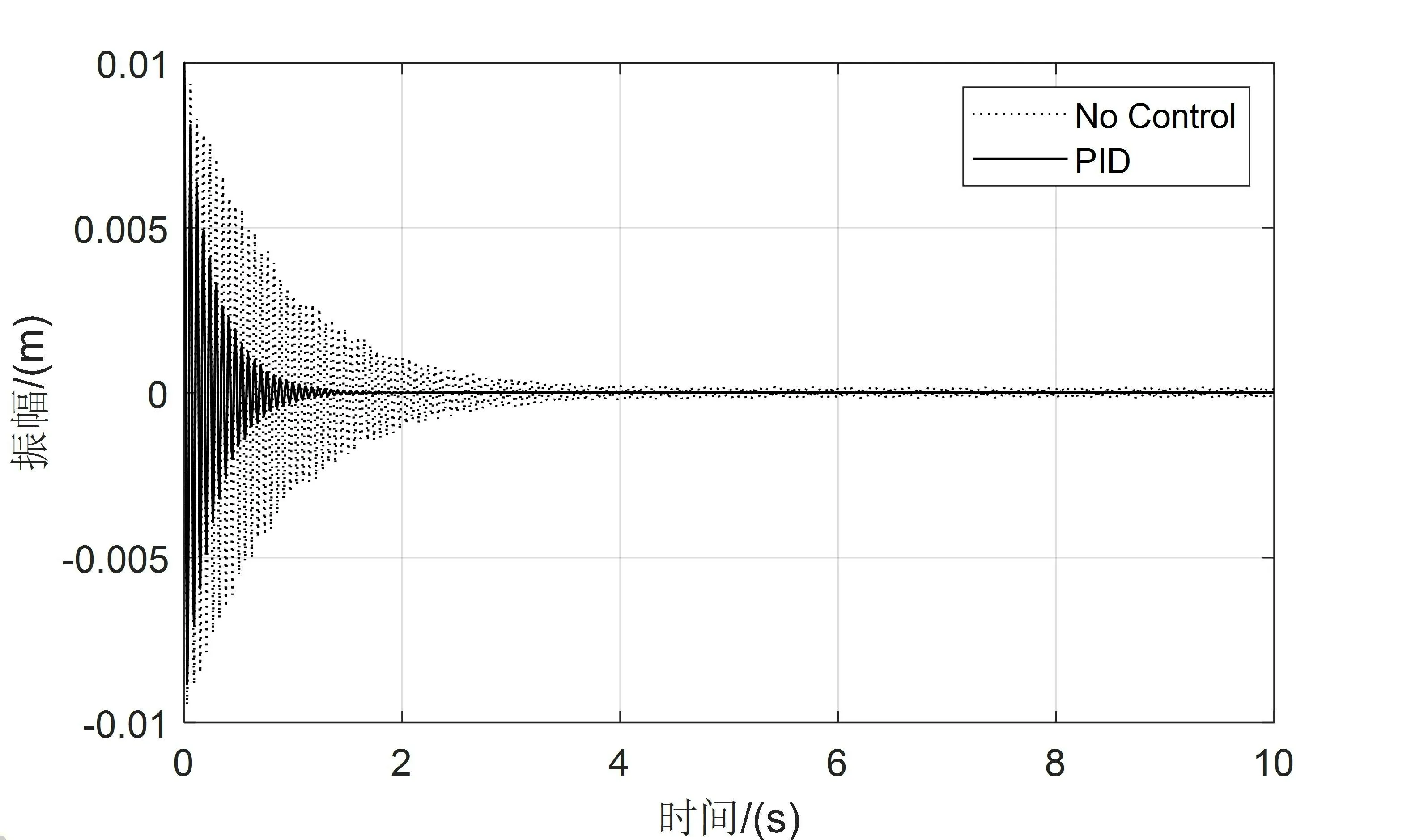
图3 二阶振动响应曲线

3.2 模糊PID整定控制

定义系统误差e和误差变化率ec变化范围定义为模糊集上的论域,对于一阶振动e,ec={-0.01,0,0.01},对于二阶振动e={-0.01,0,0.01},ec={-1,0,1},其模糊子集为e,ec={N,Z,P},子集元素分别为负,零,正。根据表3和各参数模糊控制模型,带入如下公式实现系数修正。

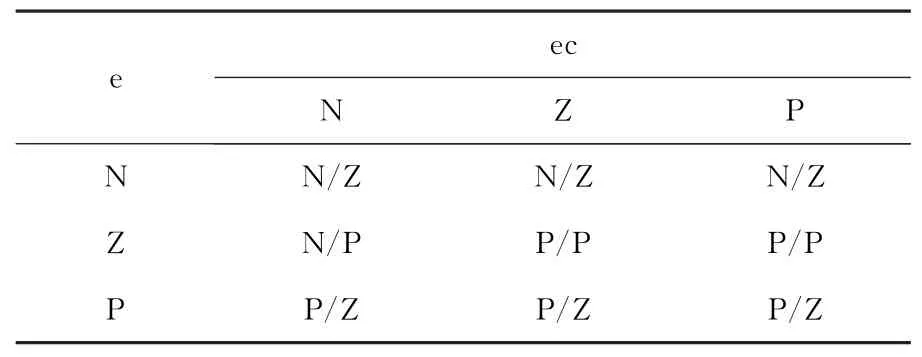
表3 Kp、Kd整定规则

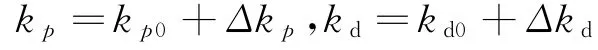
一阶振动Kp自整定范围为[30,38],Kd自整定范围为[2,3],二阶振动Kp自整定范围为[10,12],Kd自整定范围为[5,7]。模糊规则表为:

使用Simulink中模糊控制模块对系统振动进行仿真:

由图5、图6可知系统一阶振动采用普通PID控制4.5s达到稳定,采用模糊PID控制4s达到稳定,振动幅值缩减约10%,系统二阶振动两种控制均在1.5s左右达到稳定,但模糊PID控制振动幅值缩减约5%,对比可知模糊PID控制比普通PID在抑制系统振动,实现快速稳定上具有更好的效果。

图5 一阶振动响应曲线

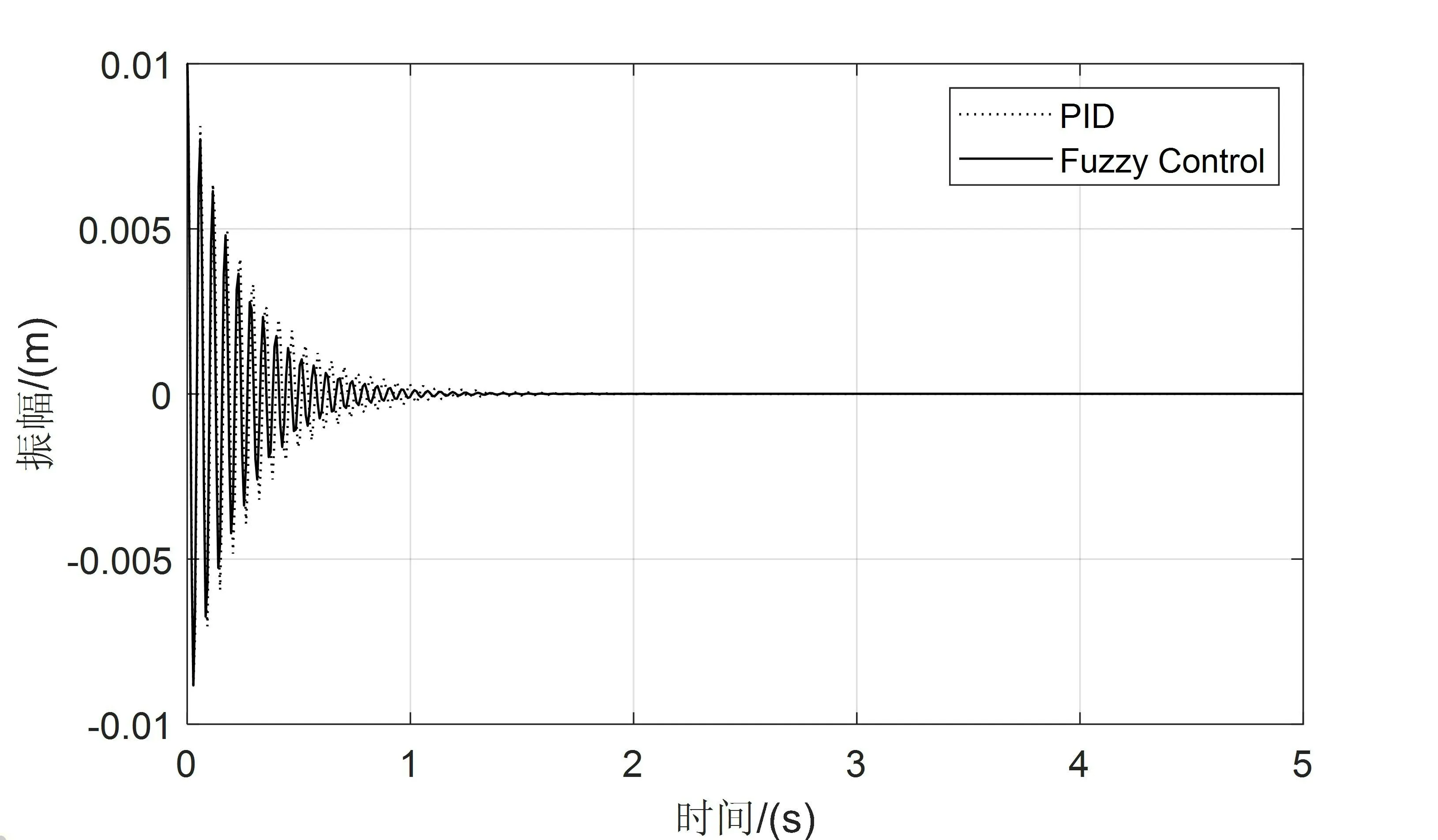
图6 二阶振动响应曲线

4 结 语

将嵌入压电材料的风力机叶片等效为悬臂梁,通过压电材料的逆压电效应进行驱动,达到振动抑制,采用PID控制器。通过对比未施加控制、普通PID控制、模糊控制三种状态下悬臂梁系统振动幅值,可知在相同条件下对系统一阶振动模糊PID比普通PID稳定时间提高约0.5s,振动幅值缩减约10%;对系统二阶振动模糊PID与普通PID均在1.5s左右达到稳定,但模糊PID控制振动幅值缩减约5%。同时模糊PID具有更好的自适应性,能够根据振动幅值进行PID参数调整。