基于实验室高光谱数据的大围山森林土壤氧化铁全量反演①

谭 洁，陈 严，周卫军，崔浩杰，刘 沛

基于实验室高光谱数据的大围山森林土壤氧化铁全量反演①

谭 洁1，陈 严1，周卫军2*，崔浩杰2，刘 沛1

(1湖南农业大学风景园林与艺术设计学院，长沙 410128；2湖南农业大学资源环境学院，长沙 410128)

氧化铁是土壤中含铁矿物的主体，是土壤发育和土壤分类最明显和最有用的指标之一。本文以湖南省大围山森林土壤为研究对象，通过实验室化学成分测定和光谱采集，在光谱预处理及组合变换基础上，采用相关性分析筛选土壤氧化铁全量的敏感波段，并分别建立多元逐步回归和偏最小二乘回归反演模型。结果表明：不同土壤光谱曲线趋势基本一致，均形似陡坎，且在420 ～ 580 nm波段，土壤氧化铁全量与光谱反射率呈负相关关系；不同的光谱数据变换方式可以提高光谱与氧化铁全量的相关性，Savitzky-Golay(S-G)平滑和去包络线相结合优于其他预处理方法；土壤氧化铁全量的特征波段主要为392、427、529、523、549、559、565、570、994和1 040 nm，偏最小二乘回归模型比多元逐步回归模型具有更好的稳定性，适合于快速估算红黄壤区森林土壤氧化铁全量。

土壤光谱；氧化铁；多元逐步回归；偏最小二乘回归

铁是岩石圈的主要元素之一，是土壤中重要的微量元素，不仅对植物的生长发育和农产品品质具有极其重要的作用，还对人体健康有着重要的意义。土壤中的氧化铁是在地表特定水热条件下，由硅酸盐类矿物经彻底风化作用而形成的重要土壤物质。由于土壤氧化铁的聚积和迁移活动受到化学风化、生物循环等因素影响，反映了土壤的淋溶过程、风化发育程度以及土壤的地带性分布特征，常被作为描述土壤发育和土壤分类的最明显和最有用的指标之一[1-3]。传统土壤化学分析方法存在着数据获取难、分析成本高、时效性差等问题，随着土壤红外光谱[4]、漫反射光谱[5]、高光谱[6]等光谱技术的快速发展，为快速、准确、定量获取土壤氧化铁全量信息提供了新的科学途径。

土壤是由不同理化性质的物质混合组成的系统，其高光谱特性受到有机质、水分、黏土矿物、氧化铁、母质及土壤质地等因素共同作用。氧化铁在土壤中常处于还原淋溶和氧化淀积的交替过程，氧化铁的形态、颗粒粗细以及是否以膜状态出现，对土壤颜色产生了很大的影响，从而也显著影响了土壤光谱特征[7]。Stone等人[8]的研究认为氧化铁的吸收带主要集中在反射光谱曲线的700 nm和 900 nm处；Hunt和Ashley[9]研究发现Fe2+在1 000 ～ 1 100 nm 附近可产生一个最常见的强而宽的谱带，Fe3+形成的吸收带主要位于 900 nm 附近；Galvão等人[10]研究巴西热带土壤时发现土壤中氧化铁含量与 1 710 nm 处的反射率的相关性显著。何挺等[11]的研究发现土壤氧化铁含量与1 550 ～ 2 320 nm 波段反射率的相关性很强，且含量越高，在400 ～ 1 200 nm 波段的反射率越低，利用红波段和蓝波段平均反射率的对数构成的土壤氧化铁指数，在高光谱图像解译中具有应用潜力；彭杰等[12]认为随游离氧化铁含量的增加，350 ～ 570 nm 波段土壤反射率降低，570 ～ 2 500 nm 波段的反射率增加。基于对土壤氧化铁的高光谱特征分析，学者们还采用多元逐步回归模型[13]、神经网络模型(BPNN)[14]、偏最小二乘回归模型(PLSR)[15]、多层感知器神经网络模型(MLP)[16]、随机森林回归算法(RFR)[17]、组合模型[18]和模糊识别[19]等方法，分别估算了土壤氧化铁全量、游离铁、针铁矿和赤铁矿含量。由此可见，土壤氧化铁全量对土壤光谱存在明显影响，可借助高光谱技术对土壤氧化铁全量进行估测。然而，目前针对森林土壤氧化铁全量的光谱反演研究相对较少，且高光谱测量易受到各种环境因素的影响，在一定程度上增加了微量元素反演的难度。因此，实验室的可见光到近红外区域高光谱反射率用于预测土壤氧化铁全量的潜力还需要有效深入地挖掘。

本研究以湖南省大围山为研究区，利用室内高光谱数据，通过运用多种平滑和数学变换形式对原始光谱进行预处理，分析土壤氧化铁全量的高光谱特征和特征波段，厘清多元逐步回归模型和偏最小二乘模型估算土壤氧化铁全量的精度差异，明确模型适用性以及最佳预处理方法，为快速定量获取红黄壤区森林土壤氧化铁全量提供高光谱模型依据。

1 材料与方法

1.1 研究区概况

大围山(114°2′ ～ 114°12′ E，28°21′ ～ 28°26′ N)位于湖南省浏阳市东北部大围山镇与张坊镇交界处，与江西省铜鼓县接壤，属中亚热带季风湿润气候，年平均气温11 ℃ ～ 17 ℃，年平均降雨量1 200 ～ 2 000 mm，年相对湿度高于83%。研究区属中山地貌，海拔范围为230 ～ 1 607.9 m，相对高差1 377.9 m，地质单元主要为燕山期花岗岩(γ)和中元古代冷家溪群板页岩(Ptln)[20]，山地土壤和植被具有明显垂直地带性。

1.2 样品采集与测试

本研究采集的样品为大围山花岗岩发育的红壤、黄红壤、黄壤、黄棕壤。在海拔177、474、545、720、860、1 078、1 210、1 382 m选择了8个具有代表性的土壤剖面设置样地，按土壤发生学划分原采集各土壤剖面样品共计 26 个，样品经自然风干，检出肉眼可见的沙砾及植物残体，研磨过100目筛。采用四分法将每个样品分为2份，1份采用三酸消解–原子吸收分光光度法测定土壤氧化铁全量[21]，另一份用于土壤光谱测量。

在人工暗室中利用SOC-710(surface optics cor­poration，USA)成像高光谱仪对土壤样品进行了高光谱图像采集。仪器光谱范围为400 ～ 1 050 nm，光谱分辨率为1.3 nm，128个波段。将土壤样品平铺至黑色塑料盒(直径10 cm，深1 cm)，水平放置在成像高光谱仪的视野中，灰板也放置于同视场角内，宽光谱石英卤素灯垂直照向土壤样品，与土样表面距离约100 cm。高光谱仪镜头光圈设置为5.6 mm，调整焦距直至显示出清晰土壤样品图像，曝光时间为自动，采集高光谱数据。通过SRAnal710e软件将土壤光谱数据进行辐射定标并将能量值转化成真实反射率，借助ENVI软件在不同的铝盒中分别选取靠近铝盒中心的50个像素点作为ROI区域建立波谱库。

1.3 高光谱数据处理与特征波段提取

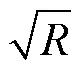
将 26个土壤样品分别依照土壤氧化铁全量进行聚类分析，并计算出每一类土壤氧化铁全量的光谱均值，获得土壤氧化铁全量的光谱响应范围。将土壤氧化铁全量分别与原始光谱反射率、数学变换光谱反射率和去包络线光谱反射率进行逐波段的相关分析，根据相关系数最值对应波长选择特征波段。相关系数计算公式如下：

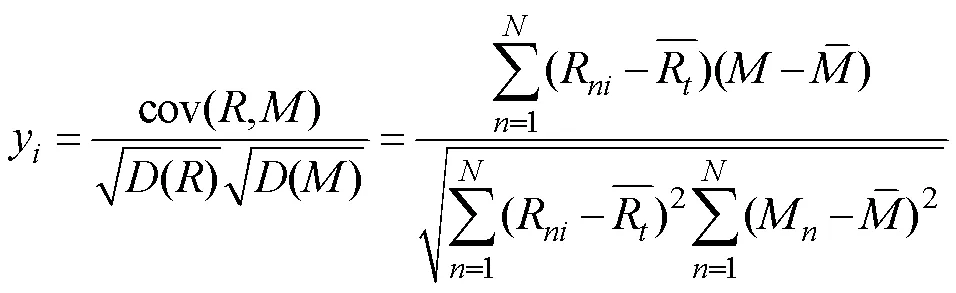
按照相关系数的显著程度可以分成以下3类：|y|<0.4为低度线性相关，0.4<|y|<0.7为显著性相关，0.7<|y|<1为高度线性相关[23]。

1.4 光谱预测模型与验证

为保证预测样本和验证样本的不同土壤类型的土壤氧化铁全量变化范围一致，将不同土壤类型的土壤，根据氧化铁全量的不同，划分为若干个小范围，统计每个范围内的样本数后，随机选取20个建模样本，6 个验证样本。基于去包络线全波段(380 ～ 1 050 nm)高光谱数据建立多元线性回归估测模型(MLR)；按照建模组与验证组比例分别为0.5:0.5和0.75:0.25，建立了两种土壤偏最小二乘回归估测模型(PLSR)。模型精度评价为决定系数2、校正均方根误差RMSEC、预测均方根RMSEP，2越大，RMSEC越小，RMSEP与RMSEC越接近，表明模型的校正及预测精度越高。根据Rossel和Webster[24]对残余预测偏差的分析可知，RPD<1.4说明模型的预测能力很差；1.4≤RPD<2.0，表明模型初步具备定量预测可能；RPD≥2.0表明模型具备较好的定量预测能力。本研究PLSR 建模和验证利用Unscrambler®X10.4完成，多元线性回归建模、数据分析在 SPSS 22.0 完成，绘图通过GraphPad Prism 8完成。

2 结果与分析

2.1 土壤氧化铁全量变化特征

由于海拔高低相差大，气候条件差异较大，大围山土壤呈明显垂直地带分布特征，低于海拔500 m多为山地红壤，海拔500 ～ 800 m为山地黄红壤，海拔800 ～ 1 200 m为山地黄壤，山地黄棕壤则主要分布在海拔1 200 ～ 1 600 m[25]。由图1和图2可知，8个土壤剖面的氧化铁全量均较高，均值为46.33 ～ 79.61 g/kg，表现为红壤>黄红壤>黄壤>黄棕壤，海拔与氧化铁全量之间呈极显著负相关关系(= –0.861 5，<0.001，= 26)。这与随着海拔升高，温度降低，相对湿度升高，土壤脱硅富铁铝化程度降低，氧化铁全量随之不断减少有关。剖面土壤氧化铁全量以剖面红壤1最高，为73.01 ～ 88.56 g/kg，剖面黄棕壤2最低，仅为46.48 ～ 50.41 g/kg。所有剖面土壤氧化铁全量均表现出AB层、B层和BC层较A层高的特征。这反映出研究区雨水丰富，淋溶作用强烈，氧化铁具有从表土层向下聚集迁移的趋势。随着土壤剖面深度的增加，外界环境和淋溶作用减弱，土壤的氧化铁全量逐步下降并趋于稳定状态，这与前人对太白山、庐山土壤氧化铁全量的研究结论类似[26-27]。

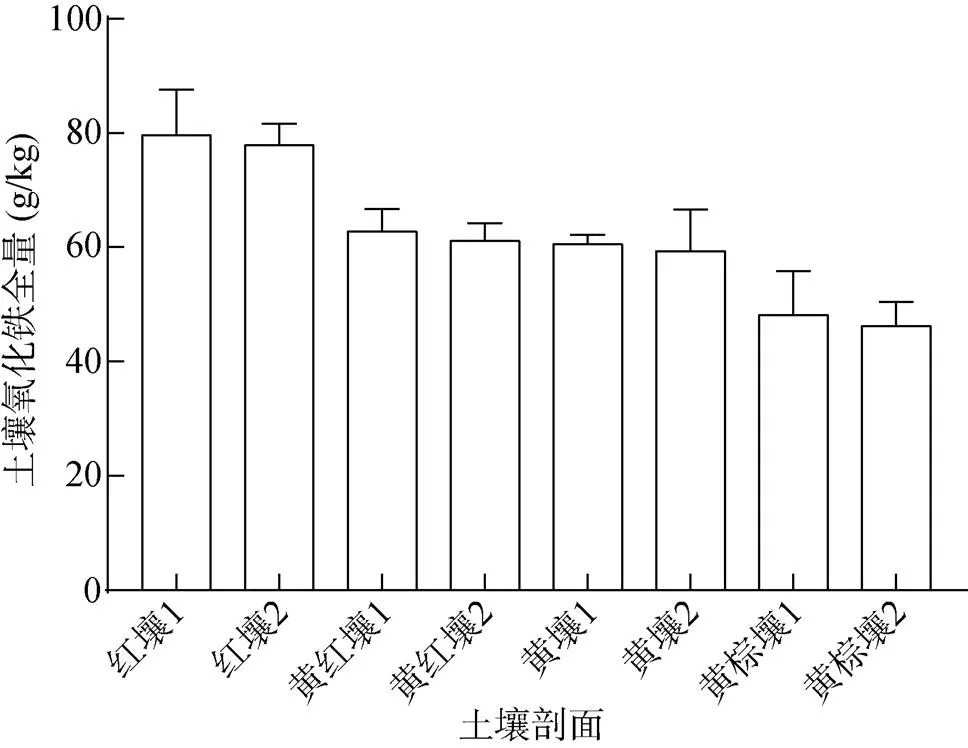
图1 各土壤剖面氧化铁全量变化特征

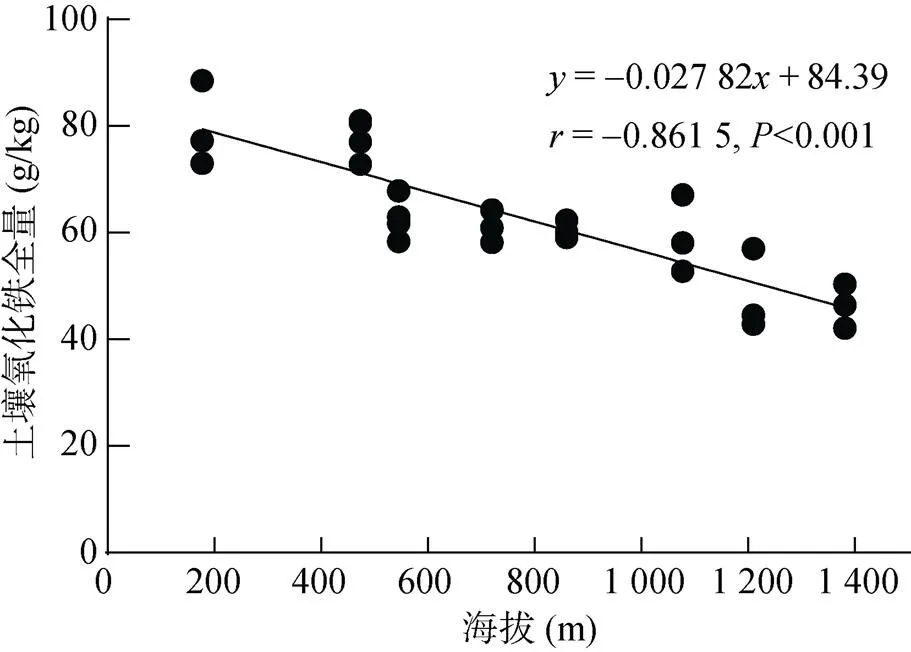
图2 土壤氧化铁全量与海拔的相关性

2.2 土壤光谱曲线特征

根据样本的土壤氧化铁全量，将样本分为 >70、60 ～ 70、50 ～ 60和 <50 g/kg 4个区间，分别计算样本在 4 个区间内的反射率平均值得到平均光谱曲线(图3)。虽然样品的氧化铁全量不同，但高光谱平均反射率曲线均呈上凸的抛物线型。在430 ～ 560 nm，随着氧化铁全量的增加，反射率呈现下降的趋势，氧化铁和反射率为负相关关系；在500 ～ 620 nm波段，反射率曲线斜率增加最快，反射率以递增的速率增加，形似陡坎；在620 ～ 780 nm 波段反射率曲线斜率略微变小，反射率以递减的速率增加；在波长780 nm处，反射率出现最大值，随后波段反射率开始下降；在波长900 nm附近，高光谱曲线存在一个微弱的吸收峰，被认为是Fe2+、Fe3+的微弱吸收峰[28]。这与土壤氧化铁全量增加时，可见光与近红外部分吸收增强，使土壤光谱反射率朝着蓝波段方向下降，导致土壤光谱反射率降低有关[7]。此结果与何挺等[11]、彭杰等[12]、郭颖等[29]认为氧化铁全量与反射光谱率为负相关一致。

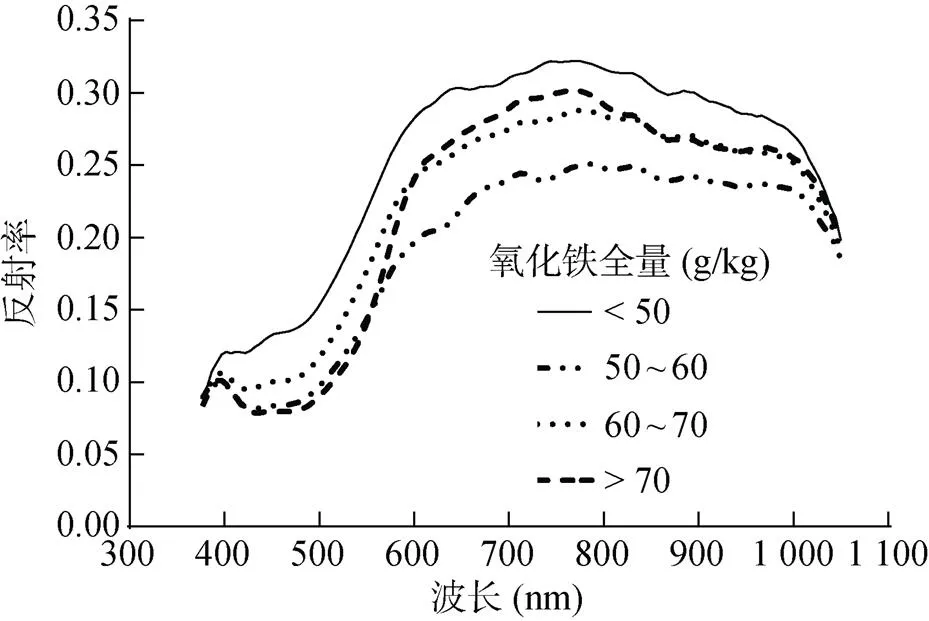
图3 不同氧化铁全量的土壤反射率均值光谱

2.3 土壤氧化铁全量的光谱特征波段

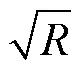
2.4 土壤氧化铁全量多元逐步回归模型

基于去包络线全波段高光谱数据，建立多元线性回归估测模型及误差分析见表1。391、565、994和1040为对应391、565、994及1 040 nm波段反射率经去包络线后的数值。通过比较2及 RPD值可以看出，模型 D 的决定系数(2)及相对分析误差(RPD)达到最大，所以模型D建立的多元逐步回归模型精度相对较高。

2.5 土壤氧化铁全量的偏最小二乘回归模型

将26个土壤样本分成建模组与验证组的比例分别为0.5:0.5(样本形式A)和0.75:0.25(样本形式B)，基于去包络线高光谱数据建立了2种偏最小二乘反演模型。由表2可知，2种样本形式的 RPD 值均大于1.4，表明样本形式A、B模型都能较好地估测土壤氧化铁全量。虽然样本形式A的建模组的决定系数R和校正均方根误差 RMSEC与样本形式B相接近，分别为0.930 6和3.643 4，但样本形式A的验证组决定系数2仅为0.630 0，验证组预测均方根误差RMSEP为7.740 0，表明该模型虽然建模效果好，但预测能力较差。样本形式 B 的建模组的决定系数2达到0.935 8，校正均方根误差RMSEC为3.419 7，验证组的2达到0.981 8，预测均方根误差RMSEP为3.155 0，表明该模型不仅建模效果好，而且预测能力也很强。可见，样本形式 B 的建模效果优于A，且形式 B 的预测效果也更佳，能够更好地估测土壤氧化铁全量。

2.6 模型的验证与优选

从多元逐步回归模型和偏最小二乘回归模型建模结果对比可见(表3)，偏最小二乘回归模型样本形式B精度更高，其验证组的决定系数(2)为0.981 8，预测均方根误差RMSEP为3.155 0，预测相对分析误差RPD为4.235 2。由两种模型预测值和实测值拟合图(图5)也可看出，偏最小二乘回归模型B的数据组相比多元逐步回归模型，建模组和验证组的预测效果更好，该结论和表2的分析结果一致。

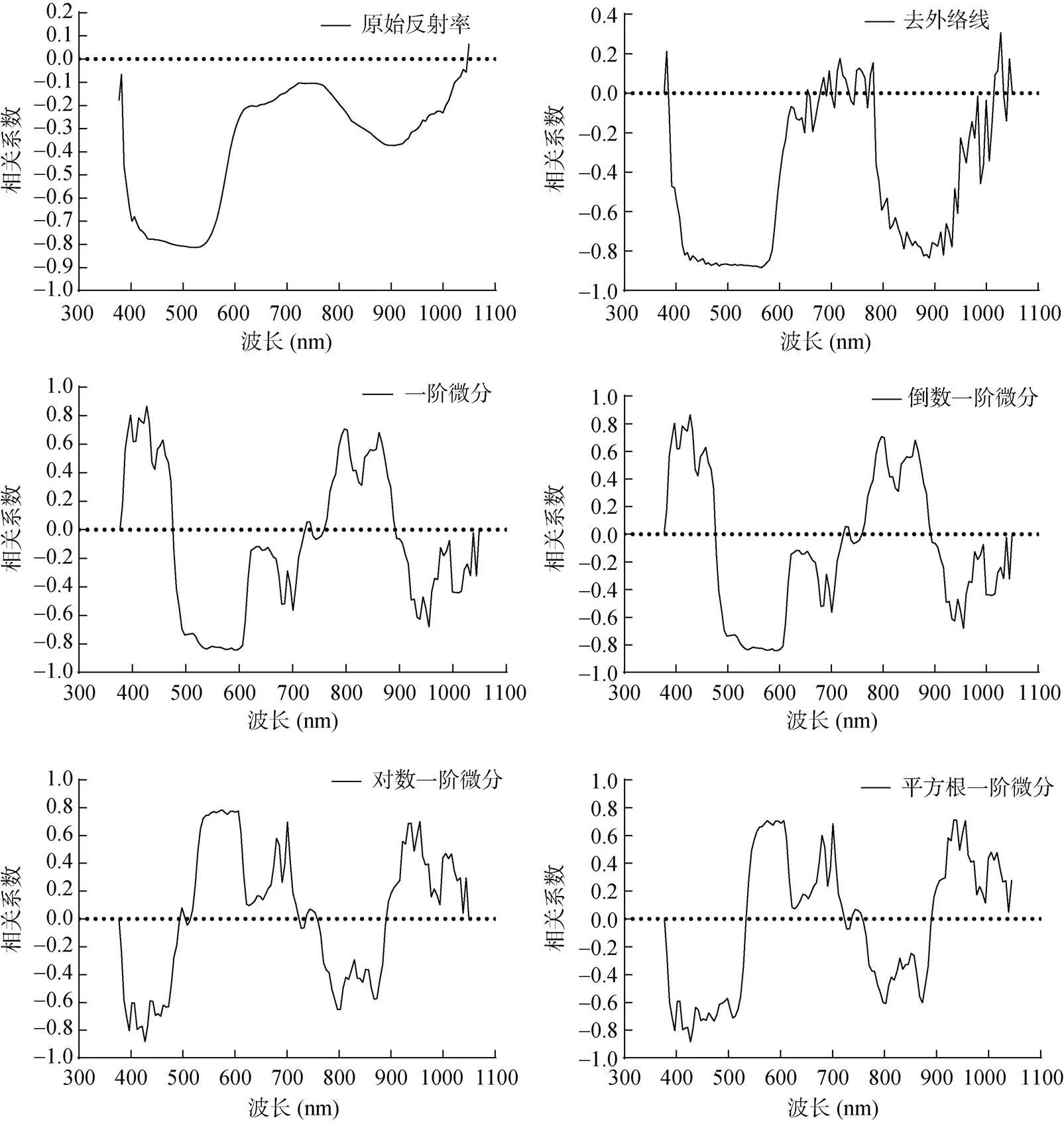
图4 高光谱变换的相关性曲线

表 1 基于去包络线的多元逐步回归模型

表 2 基于去包络线的偏最小二乘模型精度

表 3 建模结果对比

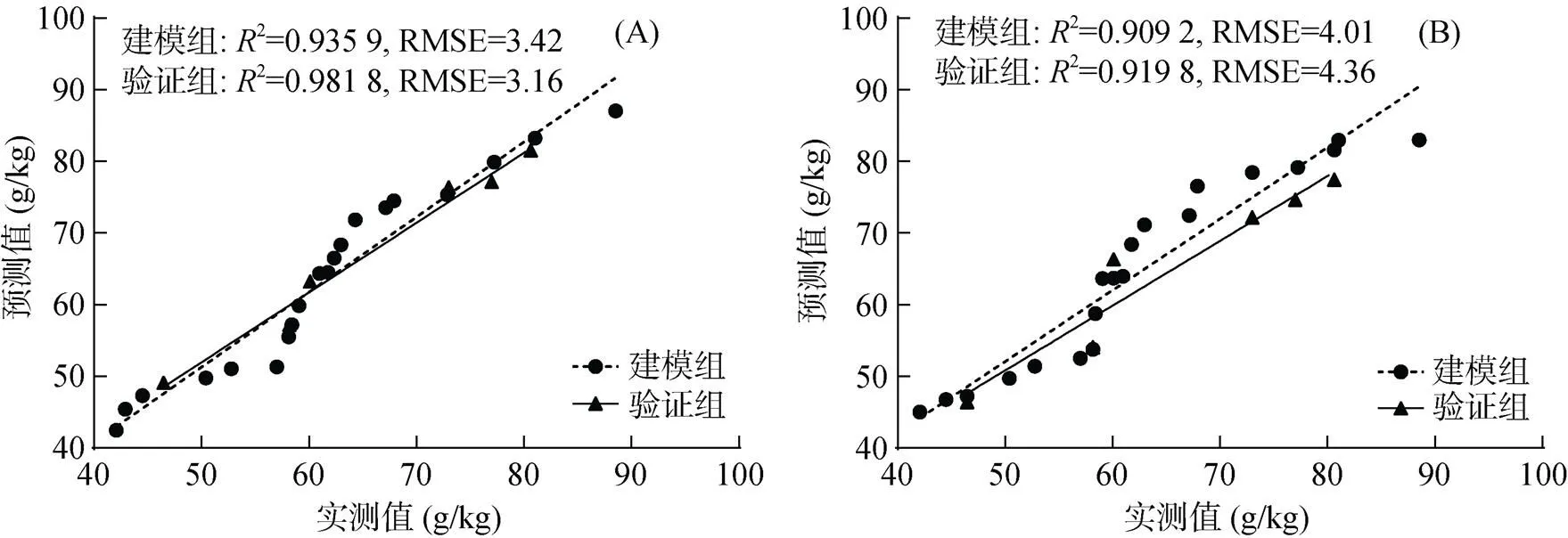
(A.多元逐步回归模型预测值和实测值拟合；B.偏最小二乘回归模型预测值和实测值拟合)

3 结论

1)不同森林土壤氧化铁全量和不同土壤类型光谱曲线在可见光–近红外波波段(400 ～ 1 000 nm)内变化趋势基本一致，均形似陡坎。在420 ～ 580 nm波段，氧化铁全量与光谱反射率呈负相关关系。

2)土壤原始反射率经过S-G平滑，并去包络线和微分处理后，光谱曲线特征差异明显，其中去包络线的处理反演效果最好。土壤氧化铁高光谱的特征波段主要为392、427、529、523、549、559、565、570、994和1 040 nm。

3)以去包络线的土壤光谱反射率为自变量建立的土壤氧化铁全量多元逐步回归模型=–115.015×565–275.853×994+231.346×1040–76.7665×391+227.603精度较好，建模组与验证组的比例为0.75:0.25优于比例为0.5:0.5的偏最小二乘回归模型。其中，建模组与验证组的比例为0.75:0.25的偏最小二乘反演模型的2最高，为0.935 8；RMSEC最小，为3.419 7；RPD最高，为4.235 2，是较为适用于红黄壤区森林土壤氧化铁全量估测的高光谱模型。

[1] Schwertmann U, Cornell R M.Iron oxides in the laboratory: Preparation and characterization[M].Wiley‐VCH Verlag GmbH: 2000.

[2] 章明奎.土壤氧化铁的形态在浙江红壤和黄壤分类中的意义[J].浙江农业大学学报, 1990, 16(1): 42–50.

[3] Terra F S, Demattê J A M, Viscarra Rossel R A.Proximal spectral sensing in pedological assessments: Vis-NIR spectra for soil classification based on weathering and pedogenesis[J].Geoderma, 2018, 318: 123–136.

[4] Todorova M, Atanassova S, Sitaula B, et al.Application of NIRS as a rapid and alternative method for prediction of heavy metals content in soil [J].Agricultural Science and Technology, 2012, 4(4): 440-444.

[5] Gupta A, Vasava H B, Das B S, et al.Local modeling approaches for estimating soil properties in selected Indian soils using diffuse reflectance data over visible to near-infrared region[J].Geoderma, 2018, 325: 59–71.

[6] 史舟, 王乾龙, 彭杰, 等.中国主要土壤高光谱反射特性分类与有机质光谱预测模型[J].中国科学: 地球科学, 2014, 44(5): 978–988.

[7] Fontes M P F, Carvalho I A Jr.Color attributes and mineralogical characteristics, evaluated by radiometry, of highly weathered tropical soils[J].Soil Science Society of America Journal, 2005, 69(4): 1162–1172.

[8] Stoner E R, Baumgardner M F.Characteristic variations in reflectance of surface soils [J].Soil Science Society of America Journal, 1981, 45(6): 1161–1165.

[9] Hunt G R, Ashley R P.Spectra of altered rocks in the visible and near infrared [J].Economic Geology, 1979, 74(7): 1613–1629.

[10] Galvão L S, Pizarro M A, Epiphanio J C N.Variations in reflectance of tropical soils: Spectral-chemical composition relationships from AVIRIS data[J].Remote Sensing of Environment, 2001, 75(2): 245–255.

[11] 何挺, 王静, 程烨, 等.土壤氧化铁光谱特征研究[J].地理与地理信息科学, 2006, 22(2): 30–34.

[12] 彭杰, 向红英, 周清, 等.土壤氧化铁的高光谱响应研究[J].光谱学与光谱分析, 2013, 33(2): 502–506.

[13] de Aldana B R V, Criado B G, Ciudad A G, et al.Estimation of mineral content in natural grasslands by near infrared reflectance spectroscopy[J].Communications in Soil Science and Plant Analysis, 1995, 26(9/10): 1383–1396.

[14] 魏昌龙, 赵玉国, 邬登巍, 等.基于光谱分析的土壤游离铁预测研究[J].土壤, 2014, 46(4): 678–683.

[15] Liu Y L, Chen Y Y.Estimation of total iron content in floodplain soils using VNIR spectroscopy - a case study in the Le'an River floodplain, China[J].International Journal of Remote Sensing, 2012, 33(18): 5954–5972.

[16] Magendran T, Sanjeevi S.Statistical and neural network analysis of hyperspectral radiometric data to characterise hematite of Singbhum iron ore belt, India[C]//SPIE Asia-Pacific Remote Sensing.Proc SPIE 9263, Multispectral, Hyperspectral, and Ultraspectral Remote Sensing Technology, Techniques and Applications V, Beijing, China.2014, 9263: 92630M.

[17] 秦倩如, 齐雁冰, 吴娟, 等.基于高光谱的土壤游离铁随机森林模型估算研究[J].土壤通报, 2018, 49(6): 1286–1293.

[18] 谢文, 赵小敏, 郭熙, 等.基于组合模型的庐山森林土壤有效铁光谱间接反演研究[J].土壤学报, 2017, 54(3): 601–612.

[19] 高开强, 徐泮林, 赵晓旭.基于模糊模式识别的土壤含铁量高光谱估测[J].测绘与空间地理信息, 2020, 43(1): 127–129,132.

[20] 赵振华, 刘伟, 赵亚辉, 等.大围山第四纪冰川地质遗迹特征及成因探讨[J].国土资源导刊, 2008, 5(6): 42–45.

[21] 鲁如坤.土壤农业化学分析方法[M].北京: 中国农业科技出版社, 1999.

[22] 王涛, 喻彩丽, 张楠楠, 等.基于去包络线和连续投影算法的枣园土壤电导率光谱检测研究[J].干旱地区农业研究, 2019, 37(5): 193–199,217.

[23] 魏建榕.经济物理学中的金融数据分析：统计与建模[D].上海: 复旦大学, 2013.

[24] Rossel R A V, Webster R.Predicting soil properties from the Australian soil visible-near infrared spectroscopic database [J].European Journal of Soil Science, 2012, 63(6): 848–860.

[25] 罗兰花, 王翠红, 谢红霞, 等.大围山花岗岩风化物发育土壤抗蚀性垂直分异[J].水土保持研究, 2018, 25(1): 62–65, 71.

[26] 雷梅, 常庆瑞, 冯立孝, 等.太白山土壤特性及氧化铁发生学特征[J].地理研究, 2001, 20(1): 83–90.

[27] 曹庆.庐山北坡土壤发生特性与系统分类[D].南京: 南京师范大学, 2012.

[28] 龚绍琦, 王鑫, 沈润平, 等.滨海盐土重金属含量高光谱遥感研究[J].遥感技术与应用, 2010, 25(2): 169–177.

[29] 郭颖, 郭治兴, 刘佳, 等.亚热带典型区域水稻土氧化铁高光谱反演——以珠江三角洲为例[J].应用生态学报, 2017, 28(11): 3675–3683.

[30] Baumgardner M F, Silva L F, Biehl L L, et al.Reflectance properties of soils [J].Advances in Agronomy, 1986, 38: 1–44.

Inversion of Iron Oxide Contents in Forest Soils of Dawei Mountains Using Laboratory Hyperspectral Data

TAN Jie1, CHEN Yan1, ZHOU Weijun2*, CUI Haojie2, LIU Pei1

(1 College of Landscape Architecture and Art Design, Hunan Agricultural University, Changsha 410128, China; 2College of Resources and Environment, Hunan Agricultural University, Changsha 410128, China)

Iron oxide is the main body of iron-bearing minerals in the soil and is one of the most obvious and useful indicators of soil development and soil classification.In this paper, forest soils in Dawei Mountain of Hunan Province were collected, iron oxide contents in soils were determined respectively by conventional chemical method and by hyperspectral inversion with models of multiple stepwise regression and partial least squares regression inversion established by screening sensitive bands after spectral preprocessing and combinatorial transformation.The results showed that soil spectral curves with different iron oxide contents all were in steep-hill shape in the whole band, iron oxide content was negatively correlated with spectral reflectance within 420-580 nm, different spectral transformation could improve the correlation, and the combination of Savitzky-Golay (S-G) smoothing and de-embedding lines was superior to other pretreatment methods in inversion.The characteristic bands of iron oxides were 392, 427, 529, 523, 549, 559, 565, 570, 994 and 1 040 nm.Partial least squares regression model had better stability than multiple stepwise regression model, and is suitable for rapid estimation of iron oxide contents in forest red and yellow soils.

Soil spectra; Iron oxide; Multiple stepwise regression; Partial least squares regression

S155.1

A

10.13758/j.cnki.tr.2021.04.025

谭洁, 陈严, 周卫军, 等.基于实验室高光谱数据的大围山森林土壤氧化铁全量反演.土壤, 2021, 53(4): 858–864.

国家自然科学基金项目(41771272)资助。

(wjzh0108@163.com)

谭洁(1979—)，女，湖南湘潭人，博士，副教授，主要从事土地/土壤环境过程及模拟研究。E-mail: 37080689@qq.com