多孔介质等效导热系数研究进展
黄 坤,白宇帅,张春云,崔 苗
(大连理工大学,工业装备结构分析国家重点实验室,辽宁省空天飞行器前沿技术重点实验室,辽宁 大连 116024)
J.Bear[1]于1983年提出多孔介质具有三个特点:多相、固体骨架大且孔隙窄和孔隙相互连接.随着人们对多孔介质认知的提升,可以将多孔介质总结成由多相材料所组成的物质,其固体部分被称为骨架,剩余空间被称为孔隙,类型包括气相和液相,孔隙可以连通,根据连通与否分为开孔和闭孔材料.根据多孔固体的孔隙率、孔隙形状及孔隙的微观结构,通常可分为三种多孔介质类型[2]:(1)泡沫型,孔隙以三维空间填充的多面体构成,固体呈连续三维网状分布(如球形、椭球形、多面体),通常称为泡沫体(如泡沫金属[3],泡沫塑料[4],泡沫碳[5-6],蜂窝体).(2)颗粒型,介质内固体以颗粒形状排列,代表单元未固结,非刚性,以相对松散堆积的组合,其中颗粒被颗粒间孔网络包围(如土壤,沙子,砾石或碎石[7]).(3)纤维型,以缝合或编织制成,或以机械,化学或物理方式将纤维粘合成随机的网状结构(如衣物[8-9],纤维编织材料[10],气凝胶[11]).
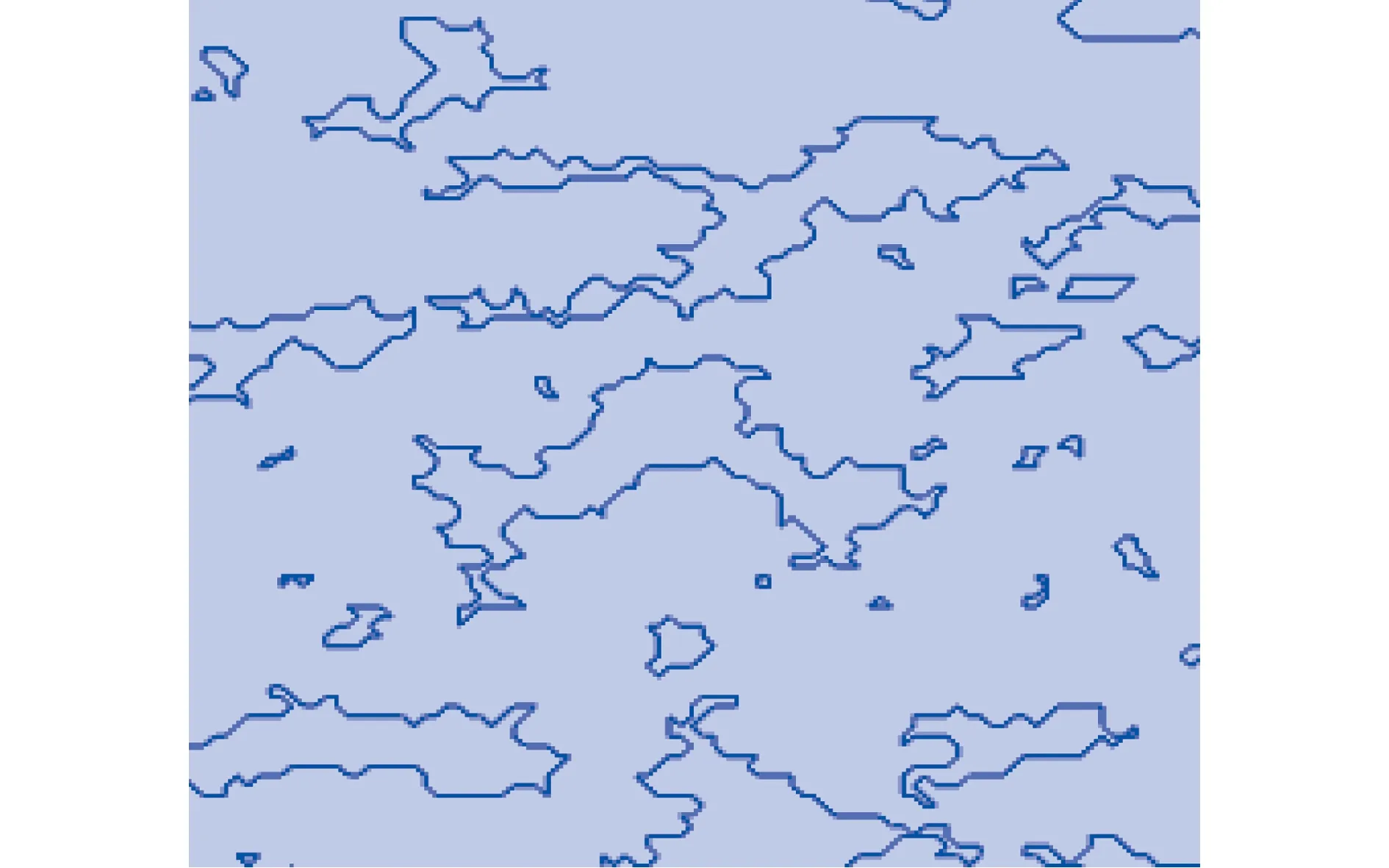
图1 通过随机四参数法生成的多孔介质(将边界平滑处理)
多孔介质具有密度小、导热系数低、隔热性好等特点,在石油开采[12]、地质工程[13]、地球环境科学与技术[14]、能源储存[15-16]、铸造加工[17]、核反应[18]和航天[19]等领域具有重要的应用价值.多孔介质内的传热不仅与固、气相介质本身的热物理特性有关,还与多孔介质中固相网络和孔隙结构有关,对多孔介质结构如图1所示,进行传热数值模拟非常困难,这是因为除了需要考虑各相的热传导,当温度较高时,需要考虑辐射传热[20]的影响,当存在流体流动时,还需要考虑对流换热的影响.采用等效导热系数来描述多孔介质的传热性能,是简化多孔介质内传热模拟的一种常用方法.然而由于多孔介质内部结构复杂,等效导热系数预测模型不具有通用性.研究表明,将经验参数(通过实验或理论方法获得)与理论模型相结合,能提高模型等效导热系数的预测精度.此外,多孔介质内部结构复杂,多孔介质的导热系数有时还呈现出各向异性[21]但是目前大部分的模型都将多孔介质视为各向同性材料,这也是目前需要解决的关键性问题之一.
多孔介质等效导热系数的研究包括实验研究、理论分析和数值模拟[22-25]三种手段,下面将对上述三个方面进行综述.
1 实验研究
多孔介质等效导热系数的实验方法主要包括以下三种:
1.1 稳态实验方法
Amani等[26]通过新型防护热板法[27]研究开孔材料孔隙率为92.7%,尺寸为80 mm×80 mm×40 mm的铝合金泡沫的导热系数,借助X射线断层摄影技术提取金属泡沫的几何特征,通过FEM方法获得其等效导热系数并与实验结果进行对比.防护热板法设备由样品、冷却板、加热板、隔热材料以及相关电气设备组成,借助珀尔帖模块来控制冷却板和加热板的温度,通过传热区域产生的一维温度梯度来准确测量等效导热系数.该实验需要1 h~2 h进入稳态条件,忽略横向的热传递,只考虑一维垂直热传递,通过热阻法计算材料的等效导热系数.由于实验尽可能地减少了自然对流的影响,此外,在低于75 ℃时可忽略热辐射的影响,因此,铝合金泡沫的等效导热系数的预测精度较高.
Rottmann等[28]使用防护热板法测量孔隙率在84%~98%的真空膨胀珍珠岩的等效导热系数,并利用瞬态热线法测量材料的表观热导率.实验温度最高达800 ℃,其在计算过程中考虑了热辐射对导热系数的影响,并且将固体的等效导热系数与表观消光系数进行联系.通过将防护热板法和瞬态热线法对比发现,防护热板法低估了辐射效应对传热的贡献,将防护热板法和瞬态热线法相结合能够很好地确定考虑热辐射影响的等效导热系数.
在防护热板中加入热流量计[29]可以提高等效导热系数的预测精度.Florez等[30]构建了一种用于测量热管烧结多孔介质等效导热系数的设备.实验装置包括三个主要部分:加热器、样品架和冷却器.尺寸为85 mm×10 mm×2 mm铜片与多孔样品串联在一起作为通量计,将热量通过热传导传递到样品.样品的热通量测量值为两个通量计测量值的平均.防护热板中的温度分布与下部通量计、样品和上部通量计测得的温度分布非常相似,所以热板可以起到辐射屏蔽作用.将系统放置在抽空的聚碳酸酯管内,避免了来自测试样品的对流传热.测试温度在20 ℃~80 ℃之间.通过连接到数据采集系统的T型热电偶测量得到温度,然后进行数据处理.
(1)
Moayeri等[31]研究了影响多孔涂层材料等效导热系数的因素,主要包括粉末形状、表面粗糙度以及孔隙率.研究中Cu-Ni粉末分为球形平滑、不规则平滑和不规则粗糙三种各类型,孔隙率包括20%、30%和40%.等效导热系数的测定实验示意图以及热电偶的位置如图2所示.
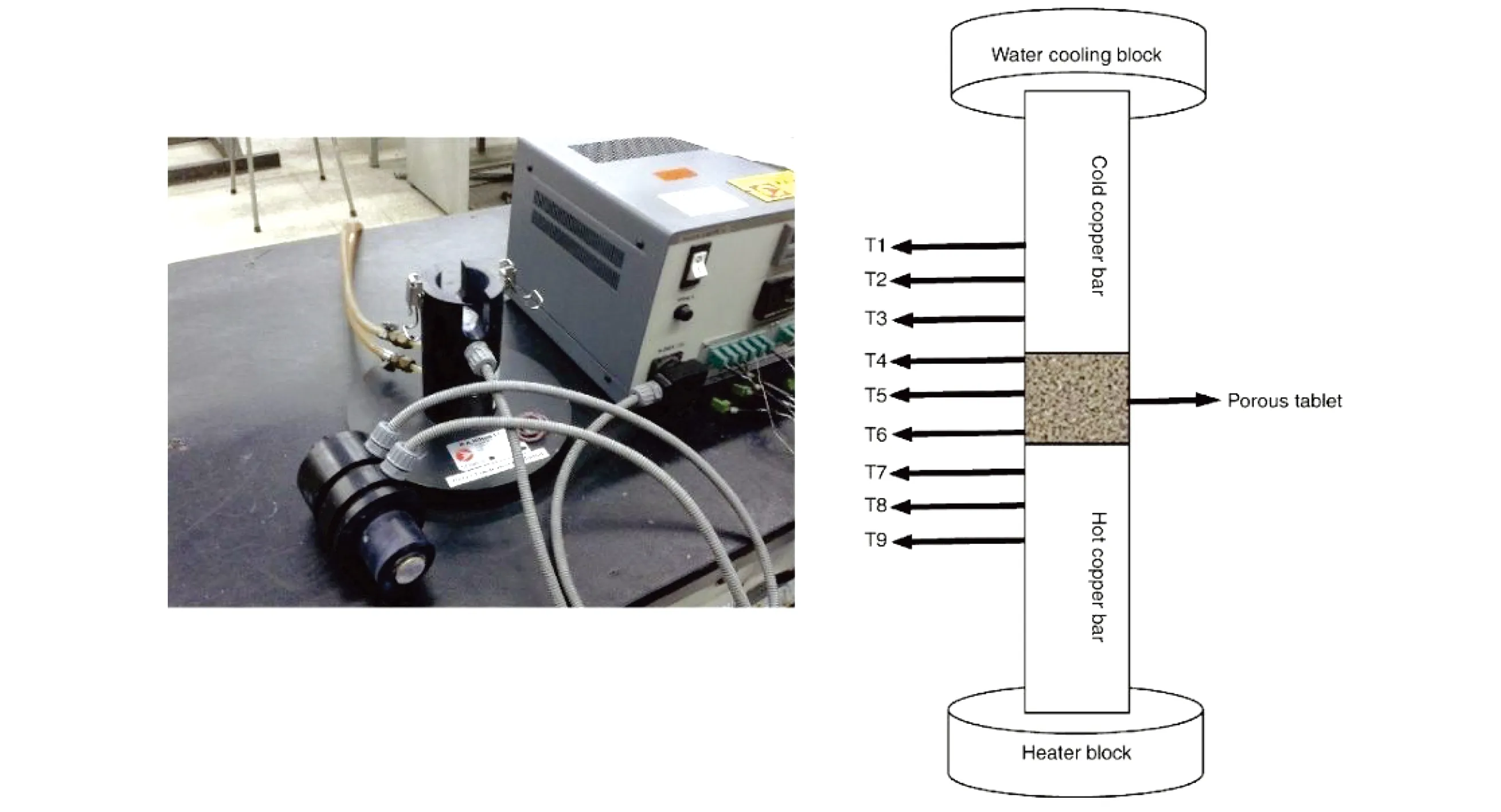
图2 测量样品等效导热系数的实验装置[32]
图2中的9个K型热电偶等间距放置,可以得到多孔介质的等效导热系数为
(2)
公式中:ΔTCu为铜棒上测量点的温度差;ΔTtablet为多孔样品上测量点的温度差;KCu为铜棒的导热系数(这里KCu=372 W/(m·K)).从实验结果可以看出Maxwell模型与等效导热系数实验值比较相近,并且球形粉末相对更加匹配该模型;表面粗糙度对等效导热系数的影响大于粉末形状.
1.2 瞬态实验方法
Penide-Fernandez等[32]研究了压缩对柔性编制陶瓷纤维的各向异性导热系数的影响,通过瞬态平面热源法[33]如图3所示.进行测量导热系数,并将实验结果与FEM建模仿真结果进行对比.实验要求在温度记录时,瞬态加热不能到达样品边界,其中最小输出功率P0=35 mW,瞬态记录时间t=10 s,样品尺寸为40 mm×40 mm,厚度为0.55 mm.实验采用热盘TPS2200分析仪进行数据采集和后处理,该分析仪准确性>95%,可重复性>99%.

图3 使用瞬态平面热源法测量导热系数[33]
对每个施加的载荷,进行了每组三个导热系数的测量,每次测量的室内温度均保持在25±1 ℃.两次测量之间使用30 min的等待时间,确保样品在施加新的压缩载荷后达到热平衡和机械松弛.由于实验过程中存在对流传热,测得的等效导热系数比采用FEM求解得到的数值大.总体上看,FEM仿真模拟与瞬态平面源测量的导热系数具有良好的一致性,应用所提出的方法可以有效地获得陶瓷织物的各向异性导热系数.
Nikpourian等[34]制备了一种高性能的多层气凝胶超级隔热材料[35],借助防护热板法设计了确定单层气凝胶毡的等效导热系数的实验方法,并采用瞬态条件下的March方法计算多层隔热材料的等效导热系数,研究了其内酚醛清漆树脂浓度对气凝胶毡的热物理性质的影响.计算多层隔热材料等效导热系数的实验方法是将多层隔热材料放置在长度0.1 m,外径0.01 m,厚度0.001 m的黄铜圆管周围,借助两个氧化铝泡沫对上下两面进行隔热,使用K型电偶获得冷却温度曲线.
根据傅里叶定律,单层气凝胶毡的等效导热系数可以表示为
(3)
公式中:Q、L、A、(Th-Tc)分别为样品的输出热通量、样品的厚度、样品的表面积以及加热器和冷却器之间的温度梯度.
通过March方法可以得到多层气凝胶毡的等效导热系数
(4)
公式中:h、rH、rc、t分别为圆柱体的高度、外半径、内半径和多层隔热的厚度.将稳态实验和瞬态实验相结合,能够找到最佳气凝胶毡层数:使用酚醛清漆气凝胶的多层隔热材料的最佳层数是12层.
1.3 考虑辐射或对流影响的实验方法
Mora-Monteros等[36]研究了陶瓷泡沫材料的等效导热系数,通过实验来测量辐射换热量如图4所示.该实验使用洛桑联邦理工学院45千瓦的高通量太阳模拟器(HFSS),该模拟器由18个单元组成,每个单元可以提供(1.0~1.5)±0.1 MW·m2峰值的辐射通量,18个单元同时使用可以使峰值热通量达到21.7 MW·m2.将样品放置在HFSS的焦点处,使用红外相机测量表面温度,热电偶测量内部温度.通过将实验与数值模拟进行耦合,可以增加样品测点的温度计算值和实验值之间的拟合度.多孔介质的孔隙率、消光系数以及使用环境对等效导热系数的影响比较大,其中使用致密涂层可以减少热辐射对导热系数测量的影响,通过将实验与数值模拟进行耦合,是处理复杂使用条件,计算等效导热系数的有效方法.

图4 Mora-Monteros 实验原理[36]
在上述的三种方法中,稳态方法需要达到热通量和内部温度的稳定,这种方法比较耗时,且对仪器设备和实验操作要求较高,常见的方法有防护热板法;瞬态方法在加热材料的同时测量材料温度的响应,其中瞬态平面热源法最具代表性,该类方法具有测试时间短、温度变化不大和对材料内部影响小等特点,能够快速、高精度地测量多孔介质材料的导热系数;考虑热辐射/热对流的影响时,实验更为复杂.
2 理论分析
多孔介质模型的构造通常采用孔道网格模型、分形理论、等效导热系数模型(如串联、并联、Maxwell-Eucken 模型等)、随机四参数生长法、基于扫描图像进行二值化等.多孔介质的导热性能一方面取决于固体骨架和孔隙内流体的导热系数,另一方面与固体骨架的空间结构(孔隙大小、形状和空间分布)也有关系,因此通常用宏观意义上的等效导热系数来描述多孔材料的导热性能.由于多孔介质内部结构在局部与电阻网络相似,可以类比电阻求热阻来计算等效热导率,其中使用串联、并联思想求多孔结构等效热导率的方法最常见.
2.1 基本模型
对于物理结构简单,只考虑热传导的各向同性非均匀多孔材料,Cleland等[37]将其归结为以下五种基本模型,如表1所示.

表1 两相材料的五个基本等效导热结构模型
表1中,K为等效导热系数,k1,k2为各相的导热系数,v1,v2为相应介质体积分数.结合这5种模型可以确定一定物理结构多孔材料的导热系数范围,其中等效导热系数计算结果以EMT模型为下限,Maxwell-Eucken 1模型为上限.基于以上五个基本结构模型,通过调整结构的体积分数可得到不同的多孔介质等效导热系数模型.通过这种方式获得的等效导热系数不依赖于经验参数,并且每种组合模型都具有相应的物理基础.
2.2 修正模型
以上的基本模型适用性很广,但对于如表1中所示的Maxwell-Eucken模型和EMT模型,计算精度不高,需要根据不同的结构进行优化和修正,其中常用的方法是等效热阻模型.首先分层计算不同结构的导热系数,再借助串并联的思想来计算周期性结构的等效导热系数,以此来估算整个模型的等效导热系数,与基本模型相比,可以提高等效导热系数的预测精度.
Chan等[38]推导了适用于饱和介质的石墨烯涂层金属泡沫的等效导热系数的理论模型,解决了以往模型无法处理石墨烯涂层的能力.由于金属泡沫结构具有一定的均匀性,可以采用半经验的方式处理其几何结构,此外,金属泡沫的结构是周期性的,可以用晶胞的导热系数来表示金属泡沫的等效导热系数.因此,可以通过单位晶格来导出等效导热系数方程.单位晶胞可分为五层结构,如图5所示.分别求出各层的等效导热系数后,可通过串联方法求出单位晶胞的等效导热系数ke,如公式(5)所示.
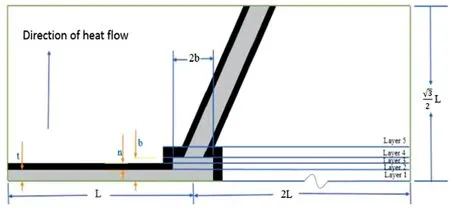
图5 晶胞分层结构[38]
(5)
公式中:ke为等效导热系数,L1,L2,L3,L4,L5分别为各层的高度.通过与实验数据进行对比,该模型计算的等效导热系数误差在0.30%~1.91%.采用该模型有助于设计包含多孔结构复合材料的热管理系统(TMS).通过研究骨架面积和石墨烯面积比对石墨烯覆盖的金属泡沫-石蜡复合材料等效导热系数的影响,发现石墨烯涂层可以显著提高金属泡沫的等效导热系数.此外,该模型可用于其他泡沫周期结构的等效导热系数的估算.
不饱和多孔介质在地热资源开发、二氧化碳封存、干燥和相变材料等领域具有广泛的应用,其中确定等效导热系数对探索其传热机理具有重要作用.Shen等[39]建立了不饱和多孔介质中导热的分型模型,基于孔隙和固相构建了多孔介质的分形毛细管束表征体单元(RVE)模型如图6所示.分形模型中的所有参数都具有特定的物理意义,分形维数的引入可以捕获非饱和多孔介质的孔隙尺度特征.这种模型假设横截面上的毛细管直径遵循分形定律,显示了各向同性多孔介质中的流动路径,其中毛细管的横截面可以视为大小不同的圆形.
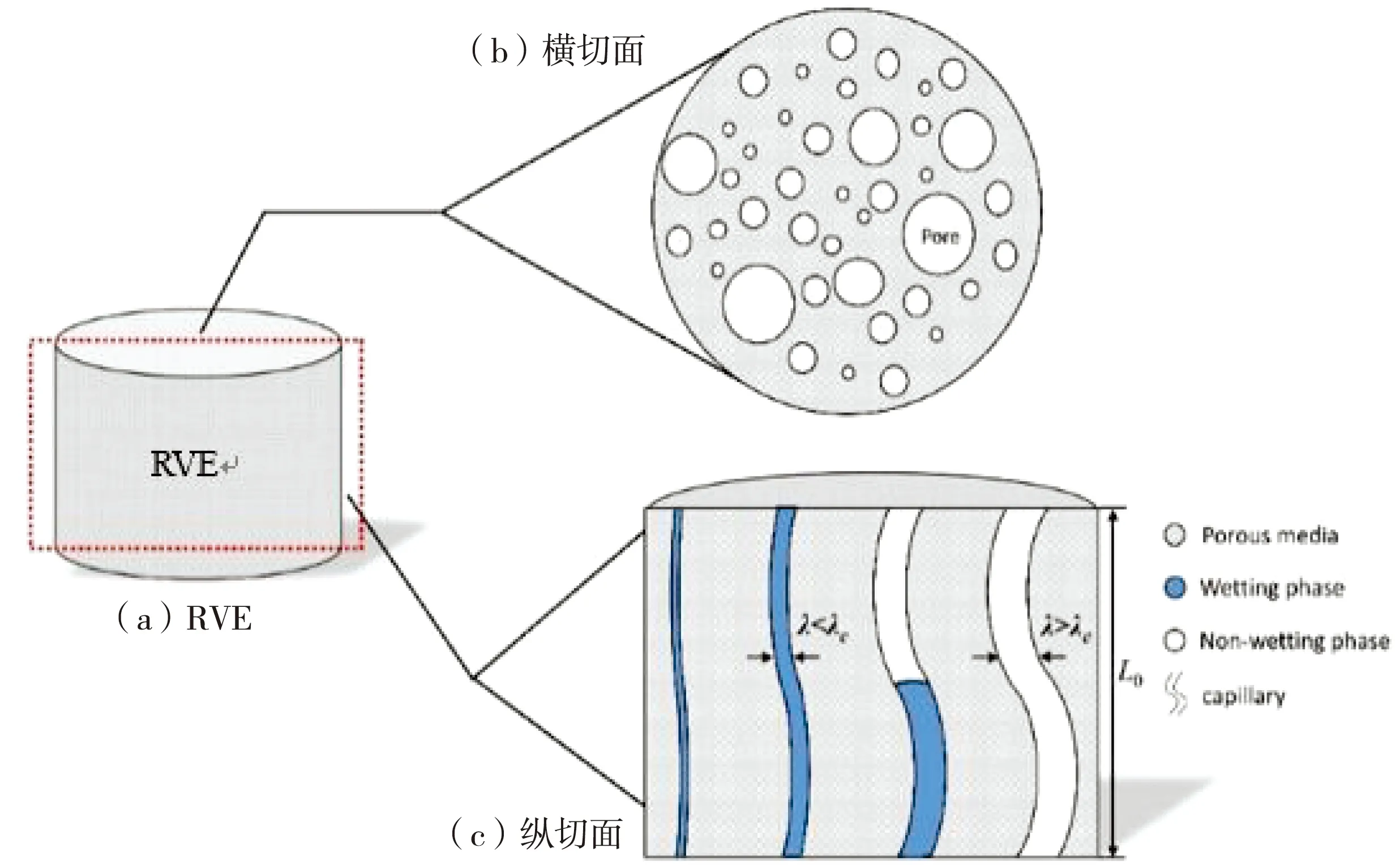
图6 多孔介质的分形毛细管束模型示意图[39]
通过等效热阻方法可以计算不饱和多孔介质的等效导热系数:
(6)
公式中:LR为RVE的代表长度;A为RVE的横截面积;Rg、Rw、Rs分别为非湿润阶段、湿润阶段和不饱和多孔介质的总热阻.该方法构建了不饱和多孔介质导热系数的通用模型,与实验数据吻合较好.通过探索等效导热系数与孔隙率以及液体饱和度之间的关系,发现等效导热系数取决于固体、气体与液相的导热系数之比.
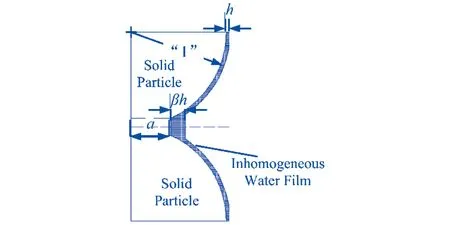
图7 具有不均匀水膜模型的粒子[40]
Chen等[40]通过瞬态平面热源法测量潮湿二氧化硅气凝剂的等效导热系数,该实验测量过程中水分变化小于1%,对模型影响可以忽略不计,通过实验数据验证预测潮湿二氧化硅气凝剂的等效导热系数的理论模型.首先构建了具有不均匀水膜结构的分形相交球的多孔介质模型如图7所示,然后推导了该模型的等效导热系数.由于气凝剂中传热过程比较复杂,借助参考温度下的部分实验数据,通过线性拟合获得经验系数
β(T)=βref+B1(T-Tref),
(7)
公式中:β为不均匀系数,是连接区域内到球形表面上的最大水膜厚与最小水膜厚度之比,下标ref指参考情况;B1为相对材料类型具有正值的经验参数.两个阶段等效导热系数为
(8)
(9)
公式中:λunit-z、λunit_xy为通过等效电路方法求得,γ可以通过公式(10)求得.
(10)
公式中:φ为材料的孔隙率.研究表明,低孔隙率模型的等效导热系数比高孔隙率的等效导热系数对含水量的变化比较敏感.与Bjurström模型[41]等预测气凝剂等效导热系数的模型相比,该方法增加了一层水膜,引入水膜相对不均匀系数β,可以还原潮湿多孔介质的模型,在预测潮湿气凝胶材料等效导热系数时的精度较高.
Kaddouri等[42]结合孔隙形态,提出了一种确定多孔材料等效导热系数的模型,结合均匀化方法计算多孔材料的等效导热系数
λeff≃λMaxl+Aln(r),
(11)
(12)
公式中:λMaxl为Maxwell模型的等效导热系数;λp、λm分别为孔和基体的导热系数;A为一个常量(A=0.7λmP(1-P)2);r为椭圆短轴与长轴之比.通过加入长宽比考虑了微观孔隙结构,与数值模拟结果吻合较好,能够更加准确地预测多孔结构材料的等效导热系数.
2.3 考虑辐射或对流的模型
在高温条件下,多孔介质内部的传热需要考虑辐射热传递.Kiradjiev等[43]对Maxwell类型的三个模型进行了概括,得到了孔隙内考虑辐射热传递的等效导热系数,结果表明,在高温条件下,辐射热传递对多孔介质的等效导热系数的影响较大.三种模型的等效导热系数计算公式如下:
(1)Maxwell辐射模型
(13)
(2)EMT辐射模型

(14)
(3)DEMT模型
(15)
公式中:k、kr分别为固体和辐射导热系数;φ为球形颗粒所占的体积分数.这些模型基于孔隙率以及孔隙内的辐射效应,得到了固体导热系数、材料孔隙率的等效导热系数表达式.通过模拟发现,随着温度的升高,等效导热系数的变化逐渐平缓,这种渐进有界的等效导热系数模型更接近实际的物理现象,对于工程应用具有重要意义,为材料设计提供新的思路.
Munagavalasa等[44]推导了双尺度多孔介质的温度平衡方程,该方程控制了非饱和流动过程中的能量分布,其中等效导热系数是方程式中一个非常重要的参数.由于使用连续性方程、动量方程和能量方程的无量纲形式,可将等效导热系数无量纲化,从而推导出无量纲化等效导热系数张量,提高了数值模拟稳定性.研究了进口速度、界面体积通量在多孔介质饱和与非饱和情况下对等效导热系数的影响,结果表明,双尺度饱和多孔介质中测得的等效导热系数可以用于流动入口后的不饱和区域,与是否存在局部热平衡无关,随着丝束间距离的增加,等效导热系数增大.
多孔介质等效导热系数理论分析大都是基于等效热阻法,首先根据多孔介质的周期性结构将其拆分成层与层,然后采用串、并联方法来求解周期性结构的等效导热系数,以此作为模型的等效导热系数,这种方法对于周期性结构非常具有参考性.当多孔介质结构非常复杂时,等效导热系数计算困难,并且考虑辐射或对流时,进一步增加了等效导热系数的预测难度,目前理论研究相对较少.
3 数值模拟
3.1 有限元法
Zhou等[25]建立多尺度有限元模型来分析基质及复合材料的等效导热系数,结合纤维增强复合材料等效导热系数的理论模型对二氧化硅/酚醛复合材料的等效导热系数进行预测.首先通过不同孔隙率下多孔基质的等效导热系数FEM分析,确定预测各种孔隙率下多孔基质等效导热系数合适的理论模型拟合函数
(16)
(17)
随后借助FEM分析微尺度的纱线模型如图8所示,以及不同基体孔隙率、温度和纤维体积分数复合材料的等效导热系数,与文献中模型进行对比并拟合,对纱线模型的横向和轴向导热系数预测选择了合适的理论模型.通过采用Lewis和Nielsen模型[45]来求解纱线的最佳几何形状参数,得出平纹复合材料面外导热系数的预测公式.

图8 纱线复合材料的多尺度建模框架[25]
Carson等[46]使用有限元方法模拟多孔介质的等效导热系数,有限差分法、边界元法等方法[47]也有相关研究.有限元方法的优点是对不规则几何形状和空间可变的物性及边界条件的适应性比较好.通过FEM研究了二维多孔介质内颗粒的大小和形状、连续相和分散相,颗粒物之间的接触程度对等效导热系数的影响,其中颗粒物的接触比颗粒大小及形状对多孔介质等效导热系数的影响大.对于分散相和连续相,其内部材料导热系数和孔隙率虽然相同,但是具有不同的等效导热系数,这为新的等效导热系数预测模型提供了参考,即多孔介质内的颗粒接触程度、分散性比内部颗粒大小或形状对等效导热系数影响更大,准确确定这些参数能更好地提高模型对不同材料的等效导热系数预测精度.
Bourih等[48]研究了莲花型多孔材料的等效导热系数,借助Kaddouri提出的改进式Maxwell模型[42]来估算莲花型多孔材料的等效导热系数,并通过两步均匀化方法来验证该模型的准确性.莲花型多孔材料是由长圆柱孔组成,孔洞沿单一方向排列,形态像莲花.他们采用了基于RVE的有限元均匀化方法预测了不同体积的多相莲花型多孔材料的等效导热系数,并与两步均匀化方法如图9所示,以及理论模型结果进行对比,发现两步均匀化方法预测等效导热系数的精度较高,证明了Kaddouri提出的预测模型能够准确地估计多相莲花型多孔材料的等效导热系数.

图9 直接均匀化方法和两步式均匀化方法[47]
Gong等[48]建立单壁碳纳米管气凝胶的三维模型,使用非晶格蒙特卡罗方法研究了多孔材料的热传导,结合数值模拟和实验,计算了四种渗透气体之间的热边界电阻.在数值模拟中,计算等效导热系数的公方为
(18)
公式中:Kg为纯气体的导热系数;Ta为沿热通量方向的温度分布;Tg为气体的温度.数值模拟研究了单壁碳纳米管气凝胶的体积分数、形态、长度和直径对等效导热系数的影响,并且开发的介观模型可以用于研究其他类型的气凝胶以及高孔隙率的多孔材料的导热性能.
Chikhi[49]使用COMSOL软件研究了多孔生物复合材料的传热性能,通过理论模型研究了孔隙率、孔隙形状和位置对等效导热系数的影响.这种多孔生物复合材料由石膏、植物纤维和空气构成,可构造一个平行六面体的RVE来研究导热性能,借助FE COMSOL 软件对Laplace方程进行数值求解获得复合材料中的温度分布.只考虑孔隙度时,数值模拟与理论模型结果一致,但是与实验结果相差较大;在考虑孔隙微观结构时,数值模拟与实验结果接近;纤维尺寸影响多孔生物复合材料等效导热系数,而在同等空气体积下,孔隙的位置和形状对等效导热系数没有显著影响.结果表明,数值模拟如果不考虑微观结构参数,很难准确预测多孔材料的等效导热系数.
3.2 Lattice-Boltzmann方法
Wang等[23,50-52]将Lattice-Boltzmann方法(LBM)用于求解多孔介质内部流固耦合传热问题,该方法易于处理多种粒子之间的相互作用和复杂的几何边界条件,但是要求各相界面处的温度和热通量具有连续性,因此各相的体积热容必须保持相同.该方法求解等效导热系数公式为
(19)
公式中:q为通过温度差为ΔT和距离为L之间的介质横截面积为dA的稳定热通量,该模型不存在经验参数.通过与实验对比,发现辐射传热占有一定的比重,在标准气压、温度286 K下,固体体积分数超过10%时,辐射传热占6%,考虑辐射传热后,模型精度有了一定的提升.将数值模拟与理论模型进行对比,发现开孔多孔介质比颗粒型多孔介质的等效导热系数更高,与实际情况相符.他们开发了随机四参数法和网状结构的随机增长方法,用来生成二维多孔介质随机颗粒结构和泡沫结构,该方法符合多孔介质的生长规律,在预测相关类型的材料时精度较高.
Lu等[53]采用LBM研究了纤维多孔介质在真空下的等效导热系数,参考了Wang等[52]的共轭传热控制方程,构建了D3Q19单元的LBM求解器,该方法只需将其中两个边界设为第一类边界条件(Thot=302 K,Tcold=298 K),其他边界设为绝热边界,LBM在处理复杂的微观结构具有一定的优势.研究了气压、纤维直径以及取向对等效导热系数的影响.结果表明,当纤维长度方向与传热方向一致性越高,隔热性能越差,取向角到90°时,等效导热系数最小;在高度真空的情况下,纤维直径与取向角之间具有耦合作用,纤维的直径越细,纤维取向对等效导热系数影响越大,但是纤维直径受纤维取向的影响较小.
Qin等[7]使用分形几何理论来构建砂岩多孔介质不同尺寸样品的模型,并且基于LBM来研究砂岩的传热性能与砂岩内部孔隙结构的关系.采用的具有多松弛时间D3Q19单元的LBM用于模拟多孔介质中的稳态流动,该方案具有较高的精度和数值稳定性[54],并且消除了边界附近的虚速度[55].使用LBM来模拟三维扫描砂岩模型的流固耦合传热,并与分形模型和Maxwell模型进行对比,研究等效导热系数与孔隙率、固相和液相导热系数的关系.通过研究发现,分形维数可用于确定多孔介质的RVE参数,并对等效导热系数有重要影响;LBM模型和分形模型可用于研究多孔介质中热传输的物理机理.结合实验结果,当Ks/Kg<10(Ks是固相导热系数,Kg是气相导热系数),分形模型比LBM得到的等效导热系数偏高,而Maxwell模型偏低;当Ks/Kg>10,分形模型与Maxwell模型得到的等效导热系数都偏低,这与Wang等[56]借助随机行走理论得到的结论相一致.
3.3 其他方法
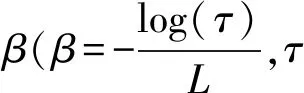
Wei等[57,58]先后用三种机器学习方法来预测通过QSGS方法生成多孔介质的等效导热系数,并结合描述多孔介质的5个重要结构特征,分析其与有效导热系数的关系.首先通过LBM计算不同孔隙大小、孔隙率和孔隙分布的多孔介质模型等效导热系数获取数据,然后通过数据训练SVR、GPR、CNN模型,分析其与Maxwell-Eucken模型、Bruggeman模型的预测误差.发现机器学习方法在预测多孔介质等效导热系数时的精度不同,其中CNN模型能够更好的考虑微观结构的相关性,精度较高.随后通过SVR和GPR模型来研究形状因子、瓶颈、主导路径、通道因数、垂直不均匀性与等效导热系数之间的相关性,通过FEM分析多孔介质等效导热系数,从结果中得出形状因子、瓶颈、主导路径与等效导热系数具有良好的正相关性,而通道因数、垂直不均匀性与等效导热系数具有一般的负相关性.通过这五种物理描述特征,将多孔介质内部微观结构转化为可以通过数据描述的参数,通过考虑这些参数能够显著提高多孔介质等效导热系数的预测精度.
Cui等[59]借助热传导反问题,通过建立最小二乘法,对蜂窝结构的等效导热系数进行预测,通过测量内部点的温度来间接预测等效导热系数等难以直接确定的热物性参数.这种方法对初值要求比较高,但是迭代速度快、计算精度高.通过与复变量求导法相结合,反演了非线性热传导问题中的边界热流密度[60],并提出确定梯度算法中松弛因子的新方法,即松弛因子自适应调节技术,提高了梯度算法的效率[61].该方法目标函数如下:
(20)

热传导反问题最早应用于系统地认识火箭表面和核反应器内部的传热问题[62].由于多孔介质微观结构及内部传热情况比较复杂,可以基于内部点的温度测量数据,通过求解反问题来间接预测其等效导热系数.目前反问题在多孔介质上已有应用,但是应用不广泛,采用反问题来确定多孔介质等效导热系数具有研究价值,特别是在工程应用上,具有一定的发展前景.
综上,关于计算多孔介质传热特性的数值模拟方法近些年发展比较充分,基于传统的有限元方法比较多,而且计算速度快,广泛用于商业软件如ABAQUS、ANSYS等,技术比较成熟,在工程上应用比较广泛.对于考虑辐射或对流的情况,目前发展了基于消光系数计算辐射导热以及基于LBM计算对流换热的数值方法,这种方法经过了可靠性验证.此外,机器学习和热传导反问题求解方法,相比于传统方法,计算精确度有一定提升,对不同种类多孔介质的应用有待进一步研究.
4 总结及展望
多孔介质以其轻质,隔热好等特点,在各种工程上应用较广,本文对多孔介质等效导热系数的研究进行总结,对多孔介质构造方法以及传热性能模拟进行简要介绍,概括了实验研究、理论分析、数值模拟这三种研究方法的优缺点:
(1)多孔介质导热性能实验根据传热类型可以分为稳态和瞬态实验方法,瞬态实验方法相对较为简单,测量时间比较短,同时测量误差也比较大;稳态实验方法对仪器设备和实验操作要求较高,同时测量导热系数精度比较高.对于辐射或对流换热等类型的传热实验装置比较少,实验比较复杂.等效导热系数的实验误差主要来自测量仪器的误差,测量误差不可消除但可以通过高精度设备来减小.
(2)等效导热系数预测的五种基本理论模型对于简单多孔结构预测精度较高,但缺少了描述多孔介质内部微观结构的参数,可以采用表征体单元方法对模型进行优化.当多孔结构比较复杂时,首先观察得到一个表征体单元,然后借助并、串联模型,计算RVE单元的等效导热系数.这种方法是将多孔介质内部简化为周期性结构,由于考虑了内部结构,计算精度比基本模型精度高,当周期性结构与多孔介质微观结构相近时,与数值模拟结果相差不大.当考虑辐射或对流换热模式时,通常将热传导与这两种方式分开计算,或者基于实验给出经验参数或表达式来提高模型的适应性,这也是目前多孔介质等效导热系数预测模型的发展方向.
(3)由于多孔介质内部结构的随机性,构造应用场景下多孔介质的精确模型是一个关键性问题.采用有限元等数值方法可以更好地帮助我们预测多孔介质内部的传热情况,结合 X 射线切片层析等技术还原多孔介质微观结构,能够显著提高等效导热系数的预测精度.通过数值模拟计算多孔介质等效导热系数并与实验所测得的结果进行对比,然后对不同的理论模型进行修正,这也是目前计算多孔介质等效导热系数应用较多的方法.
多孔介质内部传热问题比较复杂,结合实验获得多孔介质内易测的参数如部分温度,然后借助反问题求解方法得到如等效导热系数、内热源分布、复杂热边界条件等未知的参数,这是一条有效的途径.为了准确预测多孔介质或包含多孔介质的热防护系统等结构的传热性能,借助传热反问题方法来确定等效导热系数是一个有前景的研究方向,而选择合适的反问题求解方法也是该方面研究的重点.

