基于多目标算法合理配置火灾中的无人机组合

邱 雪，王永忠，赵 志，杨传军，李佳骏

(中国民用航空飞行学院，四川 广汉 618307)

0 引言

随着全球环境遭到严重破坏，火灾频发。现在火灾已成为威胁我们生存的一个重要灾害。低效率、高危险的灭火活动使得众多消防员受到伤害，且造成大量的财产损失。为了提高效率和安全，使用无人机进行监视和态势感知(SSA)已经好几年了；SSA 无人机携带有高清和热成像摄像机以及遥测传感器，可用于监测和报告前线人员的个人定位信标或更复杂的情况。同时搭载中继器的悬停无人机被用来大幅扩大前线低功率无线电的射程[3]。但是SSA无人机和中继无人机的造价高昂，因此合理配置SSA无人机和中继无人机的数量和组合至关重要。借助算法求解无人机配置模型是一项跨学科交叉研究，它对无人机规划配置方面课题研究具有重要推动意义。因而，本文将引入多目标遗传智能算法，探讨多目标遗传算法在无人机配置模型中求解精度与适应性，并分析配置结果，为火灾无人机配置规划提供参考。

首先提出了一种快速的非支配排序算法，以无人排序的方式降低了数据处理的复杂度，并将优化算法的复杂度从mN3降到mN2，加快了数据处理的过程。

采用精英策略扩展样本空间[4]。通过连接亲本和后代群体，可以通过竞争创造下一代群体，这使得在老年群体中保存的优秀基因增大，从而提高优化结果的准确性。并且保证最新种群中不会失去最好的个体，确保群体的基因水平正在迅速提高。这对于种群的发展是至关重要的。

NSGA算法中需要人为确定公共参数，存在一定的主观性，为了增加参数的可靠性，同时加入种群个体间的比较基准，因此引入了拥挤度比较算法[5]。它可以克服以上缺点，在整个Pareto域中可以得到个体的均匀分布，体现种群的分布的多样性与随机性。

1 基于无人机组合规划的多目标优化研究

多目标优化广泛应用于现实生活中。每个目标都不可能同时达到最优，每个目标都必须有自己的权重。权重分配问题是本文的研究重点，采用全局可能性搜索遗传算法，解决了传统多目标优化算法中陷入局部最优解的缺陷，同时还能够体现个体的多样性[6]。使用基于遗传算法的多目标优化策略探究 无人机组合分布问题，兼顾整体分布的同时，充分发挥无人机单元的个体优点。

目前求解Pareto边界的算法主要有两种，一种是基于数学的规划算法，这种方法过于简单，在解决实际问题过程中易出错[7]。另一种是基于遗传算法，它存在以上优点，被广泛应用于各个领域。因此本文也重点研究了目前广泛应用的NSGA-II算法。

NSGA-Ⅱ算法流程如图1所示。

分析多目标，求解并优化算法是多目标遗传算法的研究核心。重点分析相关目标函数之间的内在函数关系，结合权重分布，研究目标函数的最优趋势，探究其解的最优集[8]。NSGA-II(非支配排序遗传算法的精华)在遗传算法中具有独特的优势。一般来说，它的出现使得多目标求解更加简单、高效和明显的优点，这就是为什么它是多目标优化问题的基本算法之一。这个算法的优点主要有以下几点：

1)首先提出了一种快速的非支配排序算法，以无人排序的方式降低了数据处理的复杂度，并将优化算法的复杂度从mN3降到mN2，加快了数据处理的过程。

2)采用精英策略扩展样本空间。通过连接亲本和后代群体，可以通过竞争创造下一代群体，这使得在老年群体中保存的优秀基因增大，从而提高优化结果的准确性。并且保证最新种群中不会失去最好的个体，确保群体的基因水平正在迅速提高。这对于种群的发展是至关重要的。

3)为了克服NSGA算法里面必须人为确定公共参数的不足。另外种群个体间也需要一定的比较基准，使用拥挤度比较算法。它可以克服以上缺点，在整个Pareto域内可以得到个体的均匀分布，能够体现种群个体的优势，增加整体的多样性[9]。

1.1 多目标优化问题基本定义

1)Pareto最优：在比较解的优劣时，单目标优化直接根据适应度值大小比较不同解的优劣，但是多目标优化中目标值不只一个，根据某一个目标值决定优劣关系是不合理的，常用的比较方法是非支配排序法[10]。

2)Pareto支配：图2中给出一个双目标最小化的例子，B和A比较时，B的两个目标值都比A好，因此B肯定比A好，则称B支配A；B和C比较时，B的第一个目标比C好，但是第二个目标比C差，此时无法判断B和C哪个更好，则称B和C是互不支配的关系。另外，支配解可能不只一个，打个比方(1 000，30)和(2 000，10)这两个向量各有千秋，谁都无法全方面等于或者压制对面，但是它们可以支配其他所有的向量，那么它俩就形成了一个支配解集。这个判断方法知道就好，实际上不会采用这个方法来判断两个解的优劣，因为在目标大于2后，这个方法的效果是相当地差[11]。

图2 Pareto支配

3)Pareto前沿： 在任意一个种群里面，肯定存在着一种不受其他个体支配的解决方案。帕累托前沿(PF)是指0在目标区域中所有解的映射，如图2所示，直观理解帕累托最优解的分布[12]。其中实心的点线性分布帕累托最优解。所有的最优解的映射通过目标函数投射在Pareto最优解集之内，最优解分布于解集的边界，总体上趋于最优解的范围。如图3所示，当存在两个目标问题时，Pareto最优边界一般情况下是一条直线形状，当存在多个目标的问题，Pareto最优边界一般情况下是一个超曲面形状[11]。

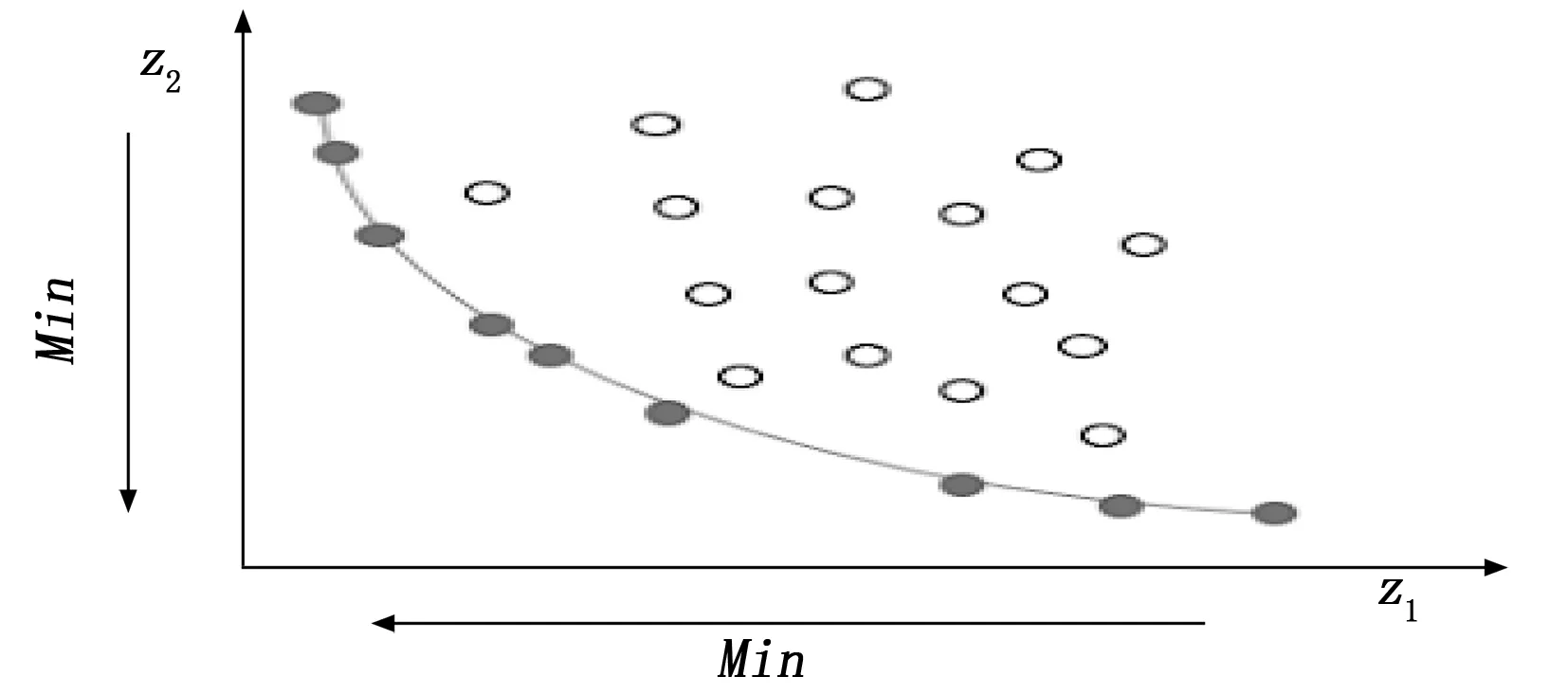
图3 Pareto前沿

4)Pareto解集：帕累托解集就是帕累托前沿所有的Pareto前沿的解不受Pareto前沿以外的解(以及Pareto前沿曲线内的其他解)的支配[13]。因此，与给予决策者更好选择的其他解决方案相比，这些非主导解决方案的目的冲突最小。同时这是必要的，至少削弱另一个目标函数，并在非优势解的基础上，削弱任何目标函数。例如，我们有两个人A和B，他们都喜欢吃西瓜。现在有8个西瓜让他们分，无论两个人怎么分，帕累托都是最优的。因为要使得A利益更大的唯一方法就是让B利益受损，即只能结合实际情况寻求较优的结果，没有最佳方案。

1.2 多目标优化的数学描述

简而言之，由多目标函数和一些相关的方程和不等式约束条件的组合就是多目标优化问题[14]。在多目标决策过程当中，通常由于要达到最好的效果有许多目标需要考虑，而有些目标之间又是相互矛盾的。这就导致多目标问题变得很复杂和困难。然而，多目标决策问题在生活中应用很广泛，因此该方法得到大量研究。解决这一决策问题的方法很多，一般来说，最根本的方法就是将多目标问题的解转化为单个目标问题的解[15]。由简入繁，先解决单目标问题，对多个单目标模型进行求解最优，构成多目标问题的最优解，便可以得到唯一目标模型的最优解。从数学角度可以做如下描述，其中目标函数表达式为：

minF(x)=(z1,z2,…,zm)

(1)

s.t.x∈Ω

(2)

目标空间：m维向量F(x)所在的空间；

以下为支配的数学定义:

定义1：解决最小化问题，需要使得一个向量v=(v1,v2,…,vn)支配另一个向量u=(u1,u2,…,un),当且仅当ui≤vi,i=1,2,…,n时且∃j∈{1,2…,n},uj

定义2：对于任意两个自变量向量x1,x2,…,Ω，如果下列条件成立：

fi(x1)≤fi(x2),∀i={1,2,…,n}

(3)

fj(x1)≤fj(x2),∀j={1,2,…,n}

(4)

则称x1支配x2。

定义3：帕累托最优解是指，一个集合中找不到一个可以支配x的解[16]。所以满足此条件的x解的集合被定义为Pareto最优解集,在目标函数空间中，Pareto前言是指由帕累托最优解集所构成的像集。

minF(x)={f1(x),f2(x),…,fn(x)}T

(5)

s.t.gi(x)≤0,i=1,2,…,p

(6)

对于已知且确定的决策变量x={x1,x2,…,xn}T，能够与n维欧氏变量空间Rn中的各个点形成对应的映射关系，经过决策优化后的目标函数f(x)能够映射m维的欧式目标函数Rm空间中的各个点[17]。换句话说，由n维欧氏设计变量空间到m维的欧式目标函数空间的映射关系便是目标函数：

f:Rn→Rm

(7)

解决多目标优化问题的三个必要步骤是：确定决策变量，寻找目标函数，补充约束条件。决策变量x1,x2,…,xn在解决实际问题过程当中可以人为设定，而且还可以根据实际问题的需要设置多个变量，不同变量具有不同的意义。他们可以任意组合得出不同的结果。但一般情况下都是直接用向量x={x1,x2,…,xn}T表示，我们把它叫做多目标优化问题的一个解。

目标函数指的是一个问题我们需要达到效果的评价指标用一个数学表达式来表达，在实际问题里面,每个性能指标都能够达到最优是决策的最佳状态。但是由帕累托解集可以知道。不可能同时达到最好，只能尽量寻求最优。因此所有的目标函数f1(x),f2(x),…,fn(x)就一起构成了多目标优化问题的目标函数向量F(X)。

约束条件是目标函数存在的属性要求，它要求决策变量需要满足这些条件，通常使用等式或是不等式来表示[18]。我们的目标是寻求可行解的集合，整体优化的可行域便是包含了满足约束条件的要求的最优可行解，由此我们需要全面考虑问题，寻求所有满足条件的约束条件。

1.3 多目标优化问题的解

单目标问题里面只需要用很简单并且常用的数学方法就可以得到最优解。但是，多目标优化问题中，单个目标之间的相互限制往往会使得一个目标得到改善但是其他目标损失较大，而牺牲其他目标的损失并且没有解决方案来实现所有目标的最佳性能。组合所有多目标优化问题的解为一个集合，我们称之为成Pareto解集，其中集合中所有的解为非劣解[19]。

如果有许多个帕累托最优解，并且没有关于问题的进一步详细信息，就很难选择哪个解是最理想的。因此，所有的帕累托最优解都是同等重要的这就是为什么多目标优化最重要的任务是优化尽可能多的Pareto解。由于这个原因多目标优化就应该解决以下两个任务：

1)找到一组尽可能接近Pareto最优域的解。

2)找到一组尽可能不同的解。

2 基于无人机组合规划的多目标模型构建及求解

2.1 仿真模拟

仿真空间：假定森林区域为一个100 km×100 km的正方形区域。

仿真无人机：一个10 W的中继器，重1.3 kg，由一架悬停在远高于地面的无人机携带，可以达到 20 km的射程。其无人机高度大约可达到17 km，则令其仿真面积为一个半径是10 km的圆；SSA无人机携带高清和热成像摄像机以及遥测传感器，可用于监测和报告前线人员的个人定位信标或更复杂的情况。一台Akme公司的原型机 WileE-15.2X 混合动力无人机装备一个5 W的无线电设备，射程可以达到4 km，高度大约2 km，仿真面积为一个以3.5 km为半径的圆。具体辐射情况如图1所示。无人机组合覆盖区域的几何模型如图1所示，搭载天线的无人机可以向下进行360°的信号覆盖，其覆盖半径记为R， SSA无人机的辐射半径记为r[21]。SSA无人机的高度记为h，中继无人机的高度记为H,中继无人机和SSA无人机之间的距离为的d，则其有效覆盖区域面积分别为：

S1=2πRH

(8)

S2=2πRh

(9)

此时天线辐射的最小波束宽度为:

(10)

(11)

(12)

(13)

根据以上公式分别画出中继无人机和SSA无人机的辐射范围,如图4所示。

图4 无人机辐射范围

在一个仿真空间范围之内，根据火灾发生的频率和地形来布局无线电中继无人机，SSA无人机在仿真空间内进行规定路径游走，在覆盖全局的条件下，根据中继无人机的无线电发射射程20 km，在仿真空间内确定中继无人机的数量；

SSA无人机在仿真空间内进行全覆盖性的游走，保证能够与中继无人机保持实时的双向通信，把收集到的地面监测、前线人员可穿戴设备的数据通过中继无人机传输到应急行动中心，同时ECO能够对SSA无人机进行远距离监控。如图5所示。

图5 无人机空间布局图

中继无人机和SSA无人机的空间位置布局大致如图，接下来利用多目标智能算法来确定一下无人机的数量配置。

2.2 智能算法确定无人机的数量组合

基于以上多目标规划的原则，对于该森林火灾中无人机配置问题，本文以经济和效率2个子目标综合优化配置无人机数量组合。我们假设某消防部门有一亿美元用于购买无人机，某公司的混合动力无人机预计在配备无线电中继器或视频和遥测功能时成本约为 10 000美元，假设一台SSA无人机的价格是300美元，一台中继无人机的价格是2 000美元。假设购买SSA无人机台，购买中继无人机台。约束函数设计如表1所示。

表1 无人机数量组合约束函数

效率最大化用下式表达：

(14)

为了更加准确地检测火灾的发生，希望无人机能尽最大可能覆盖全局。使得火情能被SSA无人机迅速检测到并传递给应急行动中心，让应急行动中心(EOC)以最佳方式指挥现役人员，以获得最佳效果和最大安全。

经济最大化用下式表达：

minz2=10000(x1+x2)+300x1+2000x2

(15)

为了能迅速检测到火情，当然是无人机越多越好。但是无人机价格高昂，因此我们需要在有效的范围内使用尽可能少的无人机，因此实现经济效益也是目标函数之一。

根据上述模型建模得出如下结论，无人机覆盖范围越大，需要的无人机越多，花费的费用就越多。具体无人机覆盖范围与无人机花费的关系如图6所示。

图6 无人机覆盖范围和无人机费用之间的关系

图6只是讨论了无人机覆盖范围与无人机花费的关系，下面要具体讨论一下SSA无人机和中继无人机不同的数量组合对无人机花费的影响。如图7可以看出，在100*100平方公里的正方形区域最多只需要32架中继无人机，257架SSA无人机，花费大约320万美元。根据该图可以看到不同的组合所花费的金额。如配备32架中继无人机，166架SSA无人机时大约花费230万美元。

图7 不同无人机组合所需的无人机费用

图7讨论了无人机数量组合对无人机花费的影响，下面要具体讨论一下SSA无人机和中继无人机不同的数量组合所形成的覆盖面积。如图8可以看出无人机的覆盖范围的趋势和无人机花费金额的趋势是类似的。即无人机越多，覆盖面积越大，同时花费也越大。由图可以看出在100*100平方公里的正方形区域内最多只需要32架中继无人机，257架SSA无人机。并且根据该图也可以看到不同的无人机组合所覆盖的具体范围。

图8 不同无人机组合的覆盖范围

3 结束语

根据以上数据进行分析得出在仿真空间之内，依靠32架无线电中继无人机和257架SSA无人机就可以实现对100*100平方公里的区域进行全局监控，但是这种组合花费巨大，需要花费大约350万美元。因此，综合考虑决定选取32架无线电中继无人机和186架SSA无人机通过图5的布局形式进行覆盖，这种方案是最经济有效的。

本文的创新性在于使用多目标规划来创建的无人机配置模型，即考虑了效率又兼顾了经济效益。利用遗传算法对目标函数进行优化求解，其中把无人机的数量组合编码作为决策变量，应用到算法中，可以直接对集合、序列、矩阵、树、图等结构对象进行操作。这样的方式有助于模拟生物的基因、染色体和遗传进化的过程，方便遗传操作算子的运用。合理且准确地给出了无人机配置方案，为有关消防部门规划提供了参考。并且针对不同的火灾范围，只需改变该模型中的一些参数即可得出不同的配置方案。同时该模型也适用于其他相关的多目标配置问题，如公司购置电脑，工厂配备产品等。但本文还存在进一步优化的可能性，可以结合不同的情况，多增加一些约束条件。比如火灾的地形，无人机在不同地形的监视情况等。