基于CFD模拟的甲烷裂解太阳能管式反应器结构优化

肖凡，贾胜坤，罗祎青，袁希钢，2

（1天津大学化工学院，天津 300354；2化学工程联合国家重点实验室（天津大学），天津 300354）

引 言

氢能作为21世纪最具有发展潜力的清洁能源之一受到普遍关注[1]。目前制氢方法主要有电解水法[2-4]、煤气化法[5-6]、甲醇裂解法[7]等。电解水制氢能量消耗大；煤气化法制氢会产生大量二氧化碳，加重温室效应，不利于“节能减排”战略的实施；甲醇裂解制氢，产物不纯，并伴有大量的碳氧化物，后续分离工艺烦琐，能耗大。而化石燃料（低碳烷烃）经高温直接裂解成氢气和炭黑不产生二氧化碳，近年来受到研究者的广泛关注。太阳辐射清洁易得，辐射集中后产生的高温可以作为裂解制氢的热能来源。因此，太阳能高温裂解甲烷制氢研究具有重要的意义和发展前景[8]。

太阳能高温裂解甲烷过程，主要是利用太阳光聚焦产生的高温热能加热反应器，促使在氩气保护下的甲烷直接发生高温裂解反应，生成氢气和炭黑[9]。太阳能的利用减少了化石能源的消耗，副反应较少，并且生成的炭黑是重要的化工原材料，因此优势显著。目前，高温裂解甲烷反应器主要有颗粒流反应器[10]、涡流反应器[11]和管式反应器[12]等形式。其中，管式反应器主要包括单管式[13]和多管式反应器[14]，因其结构简单而受到关注。在管式反应器的研究中，发现影响甲烷转化率和氢气收率的不仅包括进料气体流速及甲烷浓度、反应温度、催化剂，还包括反应器管径、入口结构[15]以及太阳能加热功率[16]等因素。与实验研究对比，计算流体力学（CFD）模拟研究具有成本低和容易实施等优点，越来越多地被用于探究各种因素对管式反应器甲烷转化率以及氢气产率的影响[17]，且CFD模拟可对实际实验进行指导[18]。

在已有研究中，为保证反应器内较低的流速和长停留时间，反应器内的流体大多为层流状态[15-19]，以实现较高甚至百分之百的转化率。但层流反应器难以满足实际工业的高通量需求，因此需要提高反应物的流速来提高反应通量。较大的流速会导致反应物停留时间更短，而受到太阳能反应器透镜尺寸等因素的限制，很难通过增加反应管的长度来提高停留时间。因此，为了保证甲烷转化率，在给定反应器管长内，通过改变流场实现反应过程的强化具有重要意义。Cao等[20]在湍流状态下，以反应过程的熵产最小为目标函数，通过虚拟外力对太阳能甲烷裂解反应器内的流场进行了优化，提高了湍流状态下的甲烷转化率，但如何将虚拟外力实物化尚未解决。

本文针对太阳能甲烷裂解反应器，通过CFD模拟的方法，开展通过主动和被动方式实现流场的优化研究，提出反应器具体建构方案，并针对实际反应器的优化设计给出定量的参考。本文首先建立了甲烷裂解反应器的湍流CFD模型，在湍流反应扩散模型的基础上，引入了碳颗粒的生成和聚集模型，实现对碳颗粒辐射吸收系数的更准确计算，利用离散坐标（DO）模型[19]对太阳能辐射场进行求解，并通过已有的实验结果对模拟结果进行了验证。然后，通过引入翅片挡板[21-22]以及射流[23]措施对流场进行优化调节，对射流流速及角度、翅片挡板高度进行优化，实现反应器内流场的优化，从而强化反应过程[24]，提高甲烷转化率。最后，以增加的反应转化率和代表强化成本的黏性耗散为指标，筛选出离散的Pareto最优解，并利用机器学习中的支持向量机回归（SVR）算法[25]对离散的Pareto最优解进行插值，得到连续的最优操作曲线以及与之相对应的射流角度和流速等操作参数。使用SVR算法进行插值相对于传统插值方法具有预测误差小、对原始数据分布要求低、可以在数据量较小时取得较好的拟合效果等优点。

1 考虑炭颗粒及其辐射的CFD模型

1.1 流体流动控制方程

假设颗粒流速和气体主体流速保持一致，且对气体的物理性质没有影响，故此反应可视为均相反应。流动模型采用基于Navier-Stokes方程的均相模型，湍流模型采用标准k-ε模型进行封闭。

流体流动控制方程主要分为连续性方程、动量传递方程以及能量传递方程。二维均相流体流动模型：

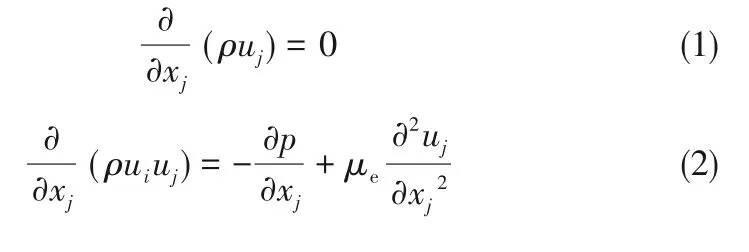
式中，μe为有效黏度，为气体混合物的黏度与湍流黏度之和，混合物黏度采用质量平均组分黏度，湍流黏度采用“标准k-ε”模型进行计算。

1.2 能量方程

甲烷热裂解反应在高温环境下具有强吸热效应，其标准状态下的反应焓变为75 kJ·mol-1[26-27]。因此，在CFD模拟中必须考虑能量方程，即：

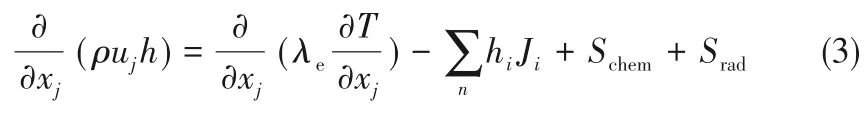
式中，hi是组分i的焓变；Schem是反应热；Srad是辐射热。

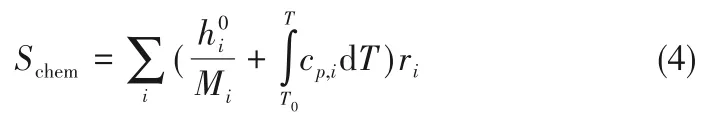
沿路程S辐射传递方程为：

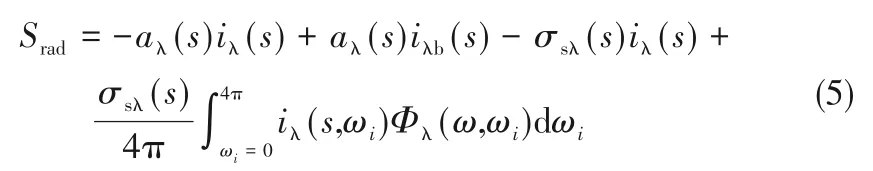
沿路程S影响辐射强度[28]大小的量包含四部分：吸收引起的衰减、发射引起的增强、散射引起的减弱以及射入散射引起的增强。式（5）采用DO模型进行求解。

1.3 组分输运方程

太阳能高温热裂解甲烷反应过程，涉及到甲烷、氢气、氩气、炭颗粒等几种组分。为了更好地模拟炭颗粒粒径对辐射系数的影响，将炭颗粒粒径划分为不同的尺寸。反应组分（甲烷、氢气、炭颗粒）的传递通过组分输运方程进行描述：

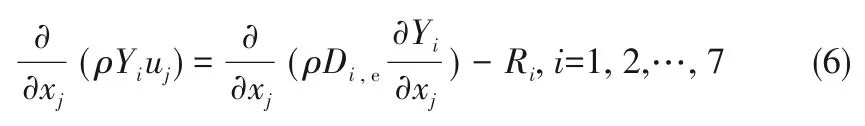
式中，Ri为反应源项；下角标i=1~5表示5种不同尺寸的炭颗粒组分，i=6和7则代表CH4和H2;Di,e为有效扩散系数：

式中，Sct为湍流Schmidt数，取为0.7，即假设湍流扩散系数与湍流黏度系数成正比。

1.4 反应源项

反应源项包含甲烷、氢气以及炭颗粒等几种组分。甲烷热裂解反应过程中，伴随着氢气和亚微米级炭黑颗粒生成，这些炭黑颗粒在气体混合物中悬浮，对流体流动、传热以及反应过程都会产生影响。实际反应中，会有少量乙烷、乙烯、乙炔等副产物生成[22,24]，但含量很小，在本文的模拟过程中予以忽略。

甲烷太阳能热裂解反应方程式可表示为：

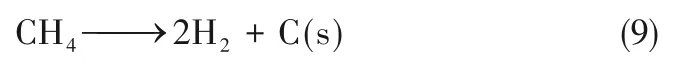
无催化剂条件下，反应动力学方程[18,26-27]为：

式中，α=0.84，Ea=259 kJ·mol-1，K0=7.68×108s-1。

甲烷直接裂解生成氢气和炭黑颗粒，组分输运方程中炭颗粒组分的源项[18]Ri为：

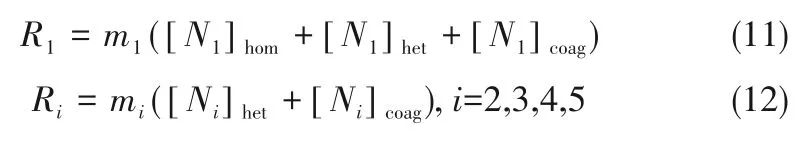
炭颗粒分为生成与聚集两部分；组分运输方程中甲烷和氢气组分的源项分别为：

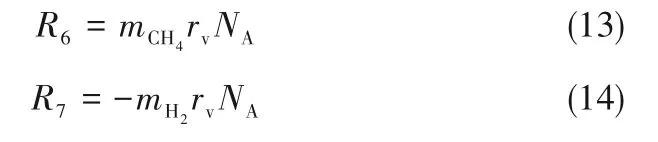
1.5 炭颗粒生成与聚集模型

在实际的甲烷裂解反应中，炭颗粒的粒径主要分布在1~9μm[18-19]。因此，考虑计算的精度与负荷的平衡，将炭颗粒组分分为5种不同的尺寸等级，对应的尺寸分别为1、3、5、7、9μm。第i等级炭颗粒的质量分数为：

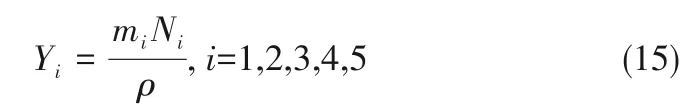
式中，mi是第i阶单个炭颗粒的质量；Ni是单位体积内i阶炭颗粒的个数。

炭颗粒会通过反应不断生成，且颗粒间也会发生聚集合并。不同尺寸的炭颗粒来源包括均相反应[N1]hom、非均相反应[Ni]het[29-30]以及颗粒的聚集[Ni][31-33]coag三部分。均相反应（成核反应）速率采用Arrhenius反应速率表达形式：

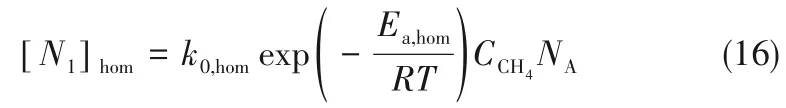
非均相反应主要发生在炭颗粒的表面（炭颗粒成长反应）：

式中，Hhet,i为甲烷扩散到级别i炭颗粒上的传质系数，具体计算公式为：

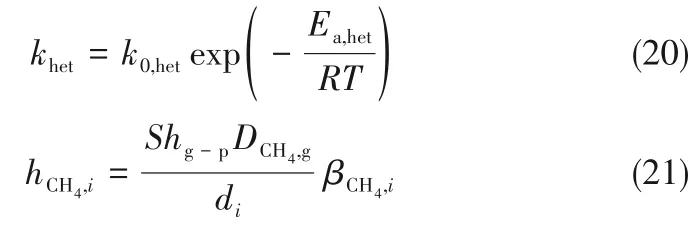
均相反应和非均相反应会形成粒径较小的初级粒子，这些初级粒子形成后会经过布朗碰撞发生聚集生成新的粒子。布朗碰撞采用菲克聚集系数模型[18-19]。其中，初级聚集单体的来源为：

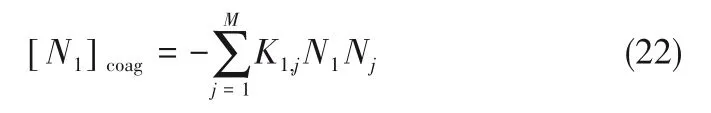
多级聚集单体的来源为：

湍流聚集系数采用菲克聚集系数：

炭颗粒的平均辐射吸收系数：

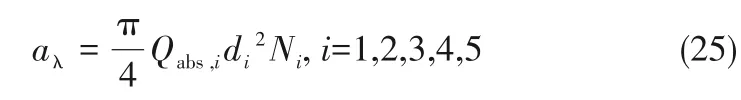
式中，Qabs指的是炭颗粒的平均光谱吸收率。本节计算得到的辐射系数将用在式（5）中，利用DO模型来求解辐射传热。

2 反应边界条件与模型验证

2.1 几何模型和边界条件

太阳能反应器几何模型如图1所示。反应管内径为10 mm，长度为100 mm。上下壁面温度为2100 K，壁面辐射发射率设为0.9，与高温下的石墨发射率保持一致。甲烷和氩气以摩尔比1∶1的比例混合后均匀进入反应器，气体流速为2 m·s-1，入口气体温度1800 K。采用充分发展的出口边界条件。

图1 太阳反应器单元模型Fig.1 Schematic diagram for a cell of solar reactor

2.2 数值模拟求解

选用ANSYS FLUENT 16.0TM商业软件求解器对控制方程进行求解。其中，压力速度耦合采用SIMPLE Scheme进行求解，梯度选择Least Squares Cell Based进行求解，压力选择Standard进行求解。连续性方程（1）、动量方程（2）、能量传递方程（3）、组分输运方程（6）选择QUICK Scheme进行求解。辐射传递方程（5）选择二阶迎风格式（second order upwind scheme）进行求解。CH4、H2以及炭颗粒组分选择一阶迎风格式（first order upwind scheme）求解。DO模型求解时每个八分圆中的天顶角和方位角采用4×4进行离散化求解。产生10套不同密度的计算网格，在相同的工况条件下进行计算，以反应管出口温度变化率不超过1%为标准进行网格独立性验证，考虑计算负荷与计算精度，选择10万个结构化网格数进行模拟。

模拟过程选择稳态模拟，甲烷转化率计算公式如下：

式中，min为进口甲烷质量；mout为出口甲烷质量。

2.3 模型验证

为验证模型的可靠性，本文以Abanades等[14]的实验为基础，以该实验太阳能反应器单元管为原型进行CFD模拟。参照文献[14]实验条件进行边界条件设置，控制方程采用式（1）~式（25）。模拟结果如表1所示，实验值与模拟值吻合很好，证明了本文模型准确。

表1 模型验证数据Table 1 Model validation data

3 太阳能管式反应器甲烷热裂解流场优化

3.1 反应管内结构优化

Cao等[20]以熵产极值为目标，获得了湍流条件下太阳能高温甲烷裂解制氢管式反应器中最优流速场，并证明该流速场可作为该反应过程优化的热力学极限。该最优流速场主要特征是，在靠近管的中间位置有一个很接近管径尺度的非轴对称涡，这种流型实现了在给定黏性耗散（即流体阻力）条件下系统的熵产速率最小，即热力学效率最高[20]。本文根据文献[20]给出的最优流场结构特征，通过在管壁增加射流以及翅片挡板的方式重现该最优流场结构。本文采取的射流和翅片挡板等措施如图2所示。上壁面距离进口33.5~35.5 mm位置处设置射流入口，上壁面52.5 mm和下壁面60 mm位置处设置翅片挡板。上述结构尺寸通过多次试算得到，其目的是获得尽量靠近文献[20]得到的流场。

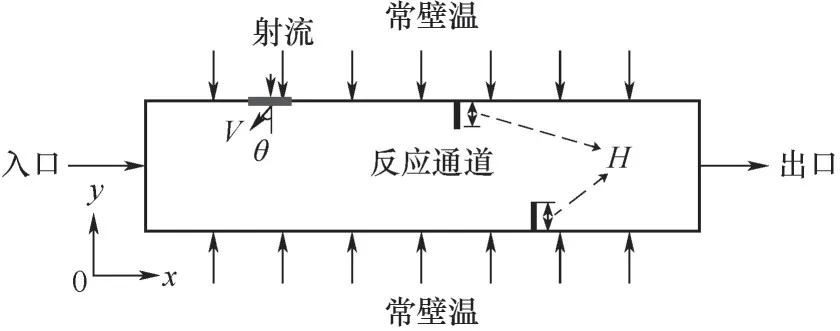
图2 太阳能反应器单元结构优化Fig.2 Optimization schematic diagram for a cell of solar reactor

3.2 优化结果与讨论

本研究对射流流速V、挡板高度H以及射流角度θ三个参数进行优化。

3.2.1 射流流速优化 在得到基本优化结构后，本文固定挡板高度为1.5 mm，射流角度为0°，射流气体组分为氩气，温度为2100 K，仅对射流速度进行优化。射流速度变化范围是1~15 m·s-1。以射流流速9 m·s-1为例进行说明，优化前、后的流线、温度、甲烷质量分数对比分别如图3~图5所示。

比较图3(a)、(b)可以看出，射流的引入导致流场发生扰动，流线图与文献[20]中给出的最优流场接近。比较图4(a)、(b)可以看出，在反应管中段，经过射流扰动后的温度明显高于优化前。甲烷裂解为吸热反应，温度升高有利于甲烷裂解反应的进行，当射流流速为9 m·s-1时，甲烷转化率可以提升约2%左右。比较图5(a)、(b)可以看出，由于前半段甲烷裂解反应更为充分，优化后的甲烷浓度在反应管后半段更低。

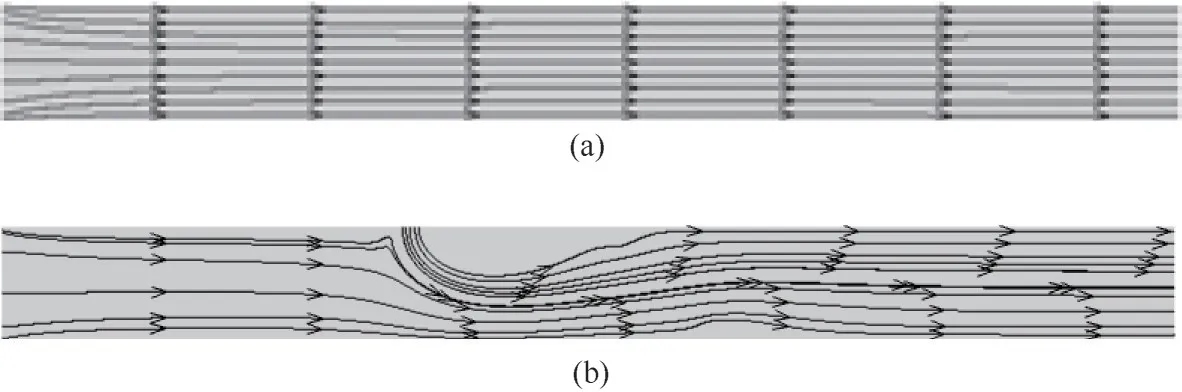
图3 无优化(a)和优化后(b)太阳能反应器内的流线图Fig.3 Streamlines in the solar reactor for the base case(a)and optimization case(b)

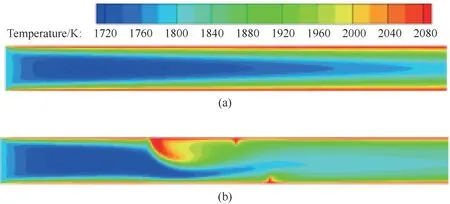
图4 无优化(a)和优化后(b)太阳能反应器内的温度分布Fig.4 Temperature profile in the solar reactor for the base case(a)and optimization case(b)

图5 无优化(a)和优化后(b)太阳能反应器内的甲烷质量分数分布Fig.5 CH4 mass fraction profile in the solar reactor for the base case(a)and optimization case(b)

图6(a)~(d)分别为反应器中x=34.5、52.5、60和90 mm位置处，不同射流速度下的温度分布对比。图7(a)~(d)是相同位置处的甲烷摩尔分数分布。由图6能够明显观测到，在y=3~6 mm范围内优化后的温度有明显的增加，且随着流速增大，温度也随之升高。优化后反应器的中后部温度升高，使得化学反应推动力增大，引起甲烷转化率的增加。

对比图6和图7可以发现，甲烷的摩尔分数分布与对应位置的温度分布大致呈负相关趋势。随着射流速度的增加，在y=2~8 mm间，甲烷摩尔分数随之降低，甲烷热裂解反应充分进行。

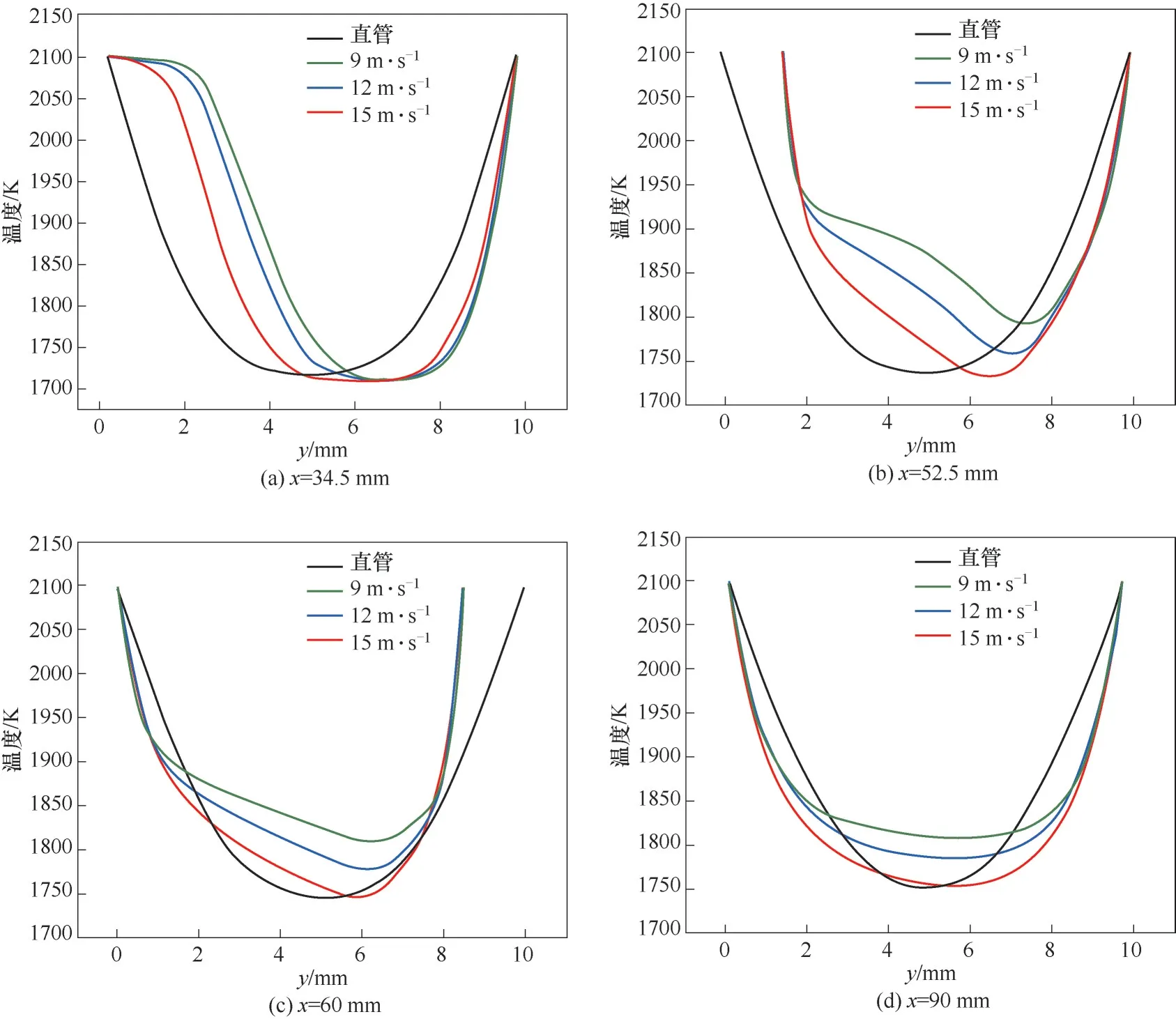
图6 无优化（直管）和优化后反应器内的温度分布对比Fig.6 Comparison of temperature distribution for the base case(straight tube)and the optimization case in the reactor

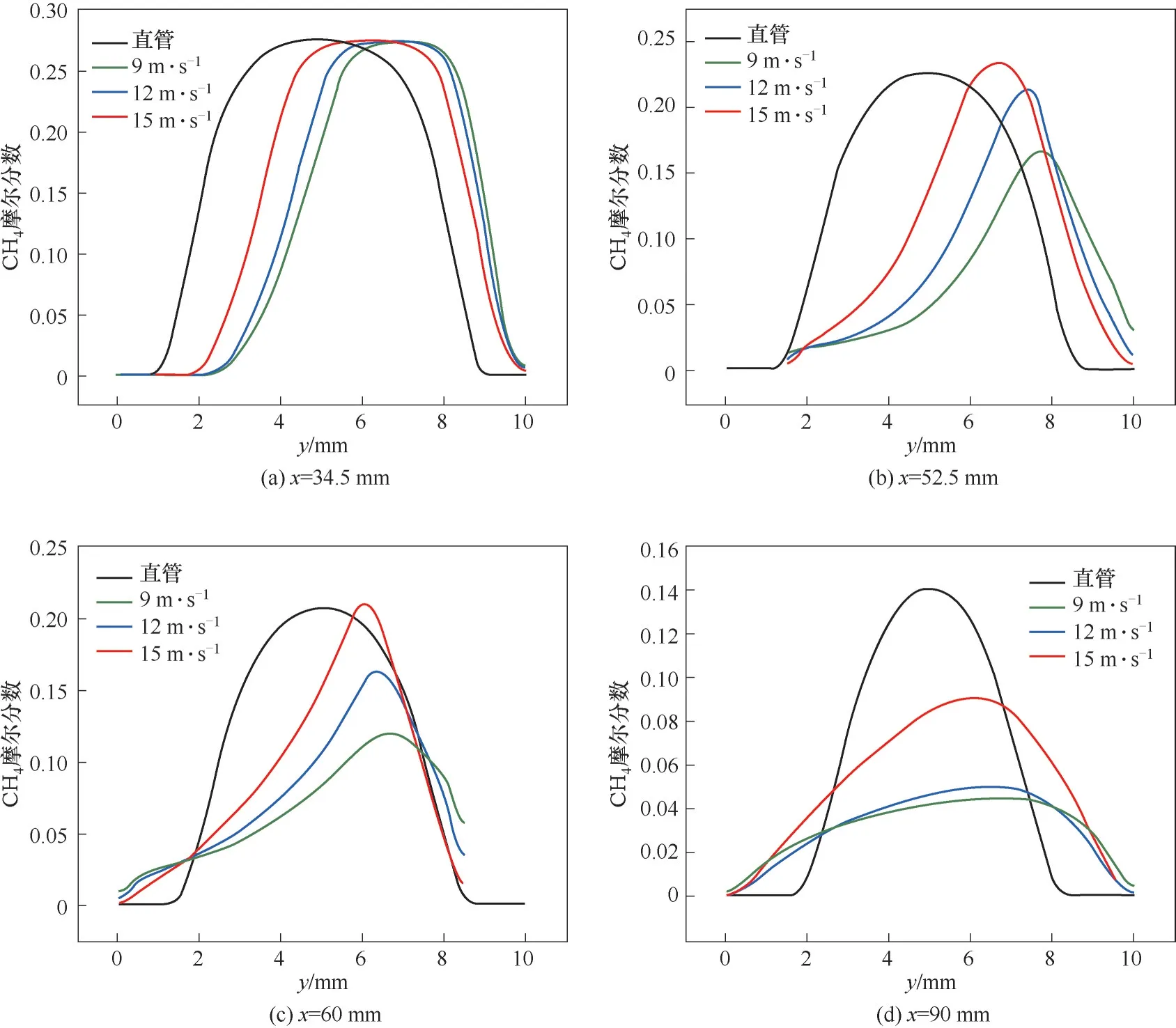
图7 无优化（直管）和优化后反应器内的甲烷摩尔分数分布对比Fig.7 Comparison of CH4 mole fraction distribution for the base case(straight tube)and the optimization case in the reactor

3.2.2 挡板高度优化 本文保持管内反应气体组分比例与质量通量不变，在不同射流流速下，对挡板高度进行优化。射流速度变化范围是1~9 m·s-1，挡板高度分别取1.0、1.5和2.0 mm，结果如表2所示。模拟发现，在确定的气体流速下，挡板高度达到1.5 mm后，增加挡板高度对甲烷转化率影响不明显。

表2 不同挡板高度在不同射流流速下甲烷增加的转化率Table 2 The increase of methane conversion rate for different baffle heights at different jet flow rates

3.2.3 射流角度优化 射流对反应器流场分布有显著影响，而挡板高度的影响甚微，因此本节对射流角度进行优化，同时挡板高度不变，设定为1.5 mm。y方向分量射流速度为1~9 m·s-1，考虑到工业气体流速极限，实际气体流速不宜超过40 m·s-1。设θ为射流方向与竖直方向的夹角，顺时针旋转为正，射流角度变化范围取-30°~85°，以5°为间隔变换角度考察计算结果。

图8给出不同射流速度和角度下甲烷转化率增加量的计算结果。可以看出，正角度的射流会提高甲烷转化率，而负角度射流会降低甲烷转化率。其原因应为正角度射流进入反应管内产生逆向扰动，流体湍动程度更为剧烈，反应更加充分，甲烷转化率会有所提高；在负角度下，射流仅会加速反应气体流出，反应停留时间减少，导致反应不充分。图8表明，在相同角度下，随着射流流速的增加，甲烷转化率呈现先上升后趋于平缓且下降趋势。这表明确定角度下射流流速并不是越大越好，存在最佳的流速，且这一最佳射流流速随射流角度的增加而增加。图8还表明，射流流速与角度对甲烷转化率增加量的影响呈现较为复杂的曲线交叉现象，在交叉区域，射流角度增加的同时射流流速需要同时增加才能提高甲烷转化率。例如，当射流速度为10 m·s-1时，射流角度80°给出的甲烷转化率增加量反而低于65°、70°和75°对应的甲烷转化率增加量。

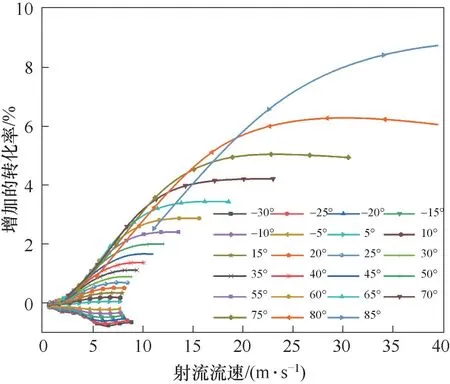
图8 不同角度及不同射流流速下甲烷增加的转化率（相同流速下，以1.5 mm挡板、0°夹角结构下甲烷转化率为基准进行比较）Fig.8 Increase of methane conversion rate in different angles and different jet flow rates

图9(a)~(c)分别为反应器中x=52.5、60和90 mm位置处射流角度优化前后温度分布对比（射流流速5 m·s-1）。图9表明，射流角度的变化会影响反应管内的温度分布。在y=2~8 mm的管内中心区域，温度随着射流角度的增加而逐渐升高。射流角度的提升会加大流场的扰动，导致高温气体在管内混合较为充分，管内温度中半段会有所提升，甲烷裂解为吸热反应，温度升高会加快反应进行，相同时间下，反应会进行得更加彻底，甲烷转化率会有所提高。

图9 流速5 m·s-1下无优化（0°）和优化后（30°,45°,60°）反应器内的温度分布对比Fig.9 Comparison of temperature distribution in the reactor without optimization(0°)and after optimization(30°,45°,60°)at a flow rate of 5 m·s-1

3.3 最优操作参数的确定

3.2节结果表明射流流速及角度的改变、挡板的引入均会强化反应过程。但是这些措施均导致流体的湍流强度的增加，因而都是以增加黏性耗散[34]，即流体流动的阻力为代价的。图10为不同射流角度和射流流速下的黏性耗散云图。图10表明，相同射流角度下，反应器内黏性耗散会随喷射流速变大而增加；相同射流流速下，反应器内的黏性耗散会随射流角度的增大而增加。黏性耗散增加意味着流体阻力以及相应的流体输送能量的增加。因此，反应器设计需要权衡反应转化率和黏性耗散，来确定最优的射流角度和流速参数。图11为甲烷增加的转化率与黏性耗散关系，可以看出，固定黏性耗散的情况下，随着角度的增大，甲烷的转化率大体呈现增加的趋势。但与图8相类似，不同射流角度的曲线会存在交叉，这意味着，相同黏性耗散下并不总是角度越大效果越好。此外，当射流角度为75°、80°和85°时，当黏性耗散增加到一定程度后，甲烷增加的转化率反而开始下降，这说明存在给定射流角度下，射流流速存在一个最优值，该最优值可使甲烷转化率的增加值达到最大，而继续增加射流流速则黏性耗散会继续增加，甲烷转化率的增加值反而下降。

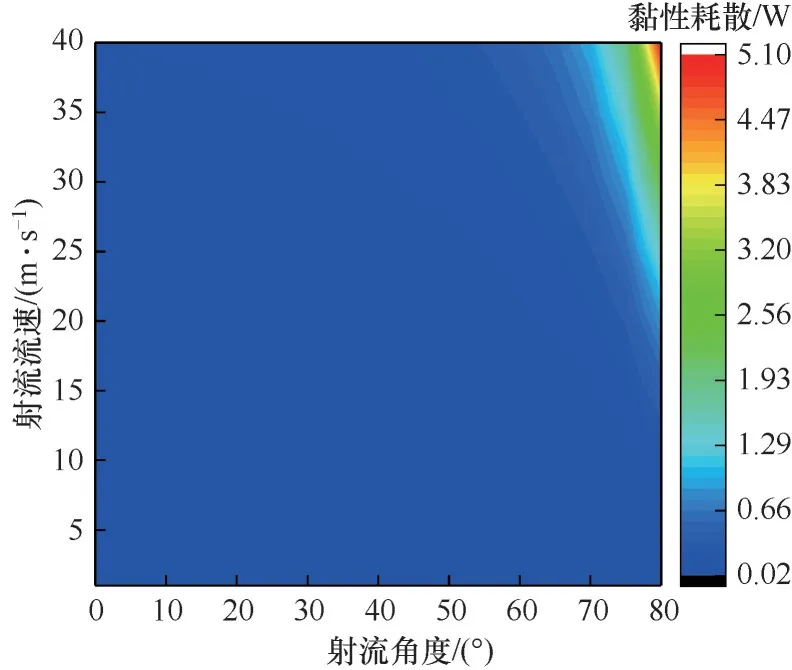
图10 不同射流角度和射流流速下黏性耗散云图Fig.10 Contour of viscous dissipation under different injection angles and injection flow rates

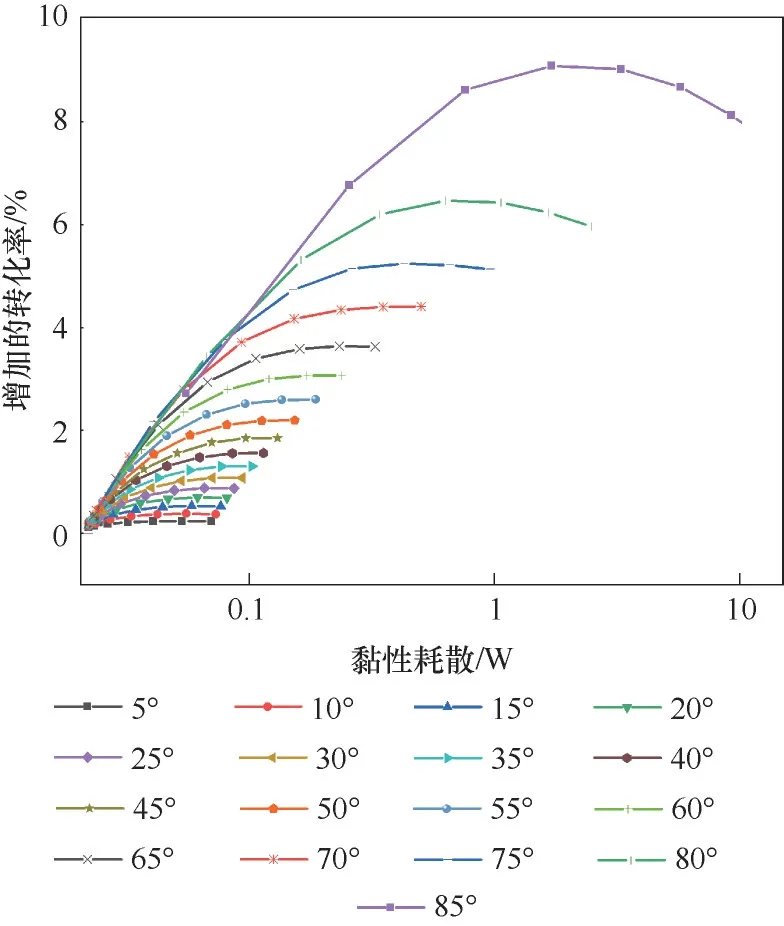
图11 甲烷增加的转化率与黏性耗散关系Fig.11 Relationship between increased methane conversion rate and viscous dissipation

以提高转化率和降低黏性耗散为目标函数，对所有模拟结果进行离散Pareto最优解的筛选，结果如图12(a)所示。因模拟工作得到的数据点有限，相应的Pareto最优解并不连续，因此，本文采取插值的方法将离散解连续化。在现有插值方法中，SVR算法插值具有预测误差小、对原始数据分布要求低、可以在数据量较小时取得较好的拟合效果等优点。本文采用SVR算法对数据点进行插值，利用SVR算法公式对黏性耗散和增加的转化率进行插值拟合，并以此得到连续的Pareto最优解曲线，如图12(b)所示。图12(b)表明，当黏性耗散低于0.7 W时，甲烷增加的转化率对黏性耗散的增加较为敏感；当黏性耗散高于0.7 W时，这一敏感度显著降低，即继续增加转化率则黏性耗散会急剧增加。因此可以选取该点附近某点作为最优设计点。射流角度为85°，垂直射流速度为3.50 m·s-1时，甲烷增加的转化率8.8%为最大值。考虑到甲烷提高的转化率为主要目标函数，取最大甲烷增加转化率的90%（增加的转化率为7.92%），作为建议操作点M（0.68 W,7.92%）。该操作点对应的垂直射流流速为2.54 m·s-1，射流角度为85°。

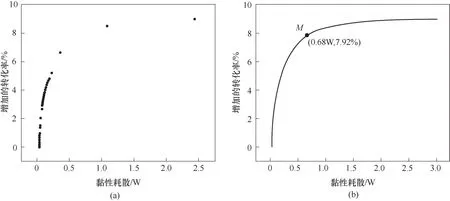
图12 甲烷增加的转化率与黏性耗散Pareto最优解Fig.12 Pareto optimal solution of increased methane conversion rate and viscous dissipation

4 结 论

本文引入炭颗粒的生成和聚集模型，考虑反应器内的辐射传热，给出了太阳能甲烷高温裂解过程更加严格的模型，并以此模型为基础对甲烷高温裂解管式反应器流场结构进行模拟。引入射流与翅片挡板对反应器管内优化流场重现来提高甲烷转化率。通过模拟，本文对射流角度、射流流速以及翅片挡板高度对甲烷转化率增加量的影响开展了研究。结果表明，翅片挡板对反应过程强化影响不明显，而射流角度和流速则对甲烷转化率有显著影响。在考察射流角度和流速对甲烷转化率影响的同时，考察了射流角度和流速对相应的黏性耗散的影响，并以甲烷转化率增加量和黏性耗散为目标，给出了两目标Pareto前沿，并据此给出了确定最优射流角度和射流流速的分析方法。在最优操作曲线上，以甲烷增加的转化率为主要目标函数，同时兼顾较小的黏性耗散，给出了建议操作点，通过本文方法设计的反应器与传统直管反应器相比甲烷转化率可提高达7.92%。

应该指出，本文研究中采用的最优流场是基于文献[20]的最优流场经重现而得，虽然引入炭颗粒产生的动力学以及辐射传热方程，但仍采用了较为简单的单相流模型。因而今后采用更加严格的多相流模型使模拟更加接近实际反应过程具有重要研究价值。

符号说明

aλ——吸收系数，m-1

CCH4——甲烷浓度，mol·L-1

DCH4,g——甲烷的扩散系数，m2·s-1

Di——组分i的扩散系数，m2·s-1

Dt——湍流扩散系数，m2·s-1

di——粒子直径，m

Ea——活化能，kJ·kmol-1

hi——组分焓变，kJ·mol-1

iλ——辐射强度，W·m-2

K——湍流聚集系数，m3·s-1

K0——反应速率常数，s-1

m——单个炭颗粒的质量，kg

N——粒子浓度，m-3

NA——阿伏伽德罗常数，6.02×10²³mol⁻¹

[N]——粒子源项，m-3·s-1

p——压力，Pa

R——热力学常数，8.314 J·(mol·K)-1

Schem——反应热，J·(m3·s)-1

Srad——辐射传热，J·(m3·s)-1

Sct——湍流Schmidt数

Shg-p——Sherwood数

T——温度，K

u——速度，m·s-1

Y——质量分数

βCH4,i——达涅克修正系数

εk——能量耗散率

λe——有效热导率，W·(m·K)-1

μe——有效黏度，kg·(m·s)-1

ν——动力黏度，kg·(m·s)-1

ρ——密度，kg·m-³

σsλ——散射系数，m-1