维里定理及其对称性
王怀玉
(清华大学 物理系,北京 100084)
0 引言
维里定理反映一个系统做稳定运动的基本规律。本文我们只讨论稳定或者叫做稳定的运动。什么叫做稳定运动,谁也没有给出严格定义。作者的理解是:稳定运动一般是指系统在运动过程中,系统的总能量总动量总角动量保持不变,系统的各部分不会运动到无限远处去。对于经典力学的系统,物体在有限的空间范围内运动,例如太阳—地球系统;对于量子力学系统,在无限远处,波函数足够快地趋于零。
对于维里定理已经有过各种各样的讨论[1-16]。维里定理先是用于经典力学系统,然后用于量子力学系统。每一种力学都有非相对论和相对论两种情况。但是,以往的讨论有以下不足。第一点,讨论都太零散,每一篇文章只谈及维里定理的一小点内容,不全面。并且,对于维里定理的物理意义认识不足。第二点,只给出了量子力学维里定理的形式,如何得到此形式没有人详细证明过。第三点,人们还没有认识到维里定理体现的对称性。维里定理的对称性,指的是关于正负动能的对称性。
众所周知,在到目前为止的经典力学中,动能只可能是正的,不可能是负的。在量子力学的薛定谔方程中,我们遇到了粒子的能量E可以小于势能V(E (1) 其中一个是正动能解,另一个是负动能解。这就明确给出了负动能的形式。本文以下,凡是一个表达式中同时出现正负符号,那么,上(下)面的符号对应于正(负)动能的情况。低动量近似后的动能形式是K(±)=±p2/(2m)。低动量运动,也称为非相对论运动,这两者是同义词。无论是式(1)的相对论形式,还是做低动量近似之后的形式,负动能就是以往的正动能的形式加一负号。注意,负动能时,动量仍然是实数而不是虚数。 长久以来,人们将非相对论运动和相对论运动看成是两种非常不同的运动。因此,通常将这两种运动割裂开来考虑。对于相对论运动和非相对论运动之间的区别和联系,作者有以下四个基本的观点。 第一,薛定谔方程在势垒区域是否适用,既没有实验上的定量验证,也没有理论上的严格推导。第二,非相对论理论只是相对论理论在低动量时的近似形式。因此,非相对论理论不是一个完备的理论,从非相对论理论本身,是看不出有没有缺陷的。相对论理论才是完整的理论。它对于动量从零到无穷大的任何数值都是正确的,所以,既适用于相对论运动也适用于非相对论运动。当它做低动量近似后,才能看出非相对论理论有什么样的缺陷。从牛顿力学本身,是看不出它有什么缺陷的。只有相对论理论出现之后,做低动量近似,才能发现牛顿力学只适用于低动量的情况。薛定谔方程应该也只是适用于低动量运动,不是一个完备的理论。从薛定谔方程本身出发,看不出有什么缺陷的。第三,相对论量子力学的负动能解和正动能解具有等同的地位,它们体现了对称性。第四,相对论量子力学方程所具有的一些性质,特别是对称性,在低动量近似时应该完全保留而不应该丢失。对称性与动量数值的大小无关。 相对论量子力学方程有三个对称性[17]。第一个是正负动能解的对称性,如式(1)所示。第二个是正负动能解的流密度数值相同、方向相反。第三个是如果势能取相反数,则方程的本征值取相反数,正负动能解交换。作为相对论量子力学方程的一个低动量近似的薛定谔方程,则没有这三个对称性。可知,薛定谔方程有缺陷。 根据第三个观点,作者圆满解决了一个相对论粒子遇到势垒时的克莱因佯谬[18]。作者根据另外三个观点,将相对论量子力学方程做低动量近似并进行了仔细的研究[17]。与经典力学相比,量子力学有着更为丰富的内容。这是因为相对论量子力学方程比狭义相对论力学多出来以下两个内容。第一,狄拉克方程除了正动能解,还有负动能解。第二,量子力学中有自旋。波函数必须用旋量的形式来表达。 相对论量子力学方程的正动能解,其低动量近似是薛定谔方程,这是有经典对应的。这一点已为大家所熟知。大家还没有认识到的一点是,负动能解也应该有低动量近似。近似的结果,是负动能薛定谔方程[17]。这就扩展了我们关于量子力学的知识。作者还提出了探测负动能电子的实验[17]。将负动能薛定谔方程与薛定谔方程相结合,就继承了前述的相对论量子力学方程的三个对称性。 到目前为止,我们所熟悉的系统中,组成系统的粒子都具有正动能。这样的系统的热力学性质和统计力学性质已经有了充分的研究。这类系统的能谱的特点是:有下限而没有上限。而相对论量子力学方程的负动能解和负动能薛定谔方程的能谱的特点是:有上限而没有下限。对于这一类系统的热力学和统计力学,作者也做了研究[19]。 在经典力学中,牛顿力学和狭义相对论分别描述宏观物体的低速运动和相对论性运动。在量子力学中,薛定谔方程和相对论量子力学方程的正动能解分别描述微观粒子的非相对论和相对论运动。作者发现,可以在量子力学的方程中,令普朗克常数趋于零(ћ→0),这一步骤叫做经典近似。做经典近似后,可以从量子力学方程得到经典力学的运动方程[20]。 以上这些,都是具有正动能的物质的运动。相对论量子力学方程的负动能解和负动能薛定谔方程,描述具有负动能的微观粒子的运动。同样,对于这样的量子力学方程做经典近似,就可以得到负动能宏观物体的运动方程[20]。我们称之为负动能物体的经典力学。它也分为低动量运动和相对论性运动。作者认为负动能物质就是暗物质。所以,我们宇宙中的物质具有正动能—负动能的对称性,也就是说,我们的宇宙具有物质—暗物质对称性。暗物质是因为它们具有负动能,所以,我们才观察不到。以后,作者将撰文研究说明,暗物质为什么是暗的。 既然物质可能具有负动能,这一点就应该在维里定理中反映出来。本文的目的是对于维里定理有一个全面的研究。既有经典力学也有量子力学,每种力学都包括低动量运动和相对论运动。作者要证明,量子力学和经典力学的维里定理具有同一起源。有的文献在讨论量子力学系统时,用费曼—海尔曼定理来推导维里定理的内容,而经典力学中是没有费曼—海尔曼定理的,这就显得经典力学和量子力学系统似乎有不同的公式起源。 作者还要强调维里定理关于正负动能的对称性。这种对称性是来源于前述的物质运动的基本方程关于正负动能的对称性。 对于每一种具体的情况,只给出单体和二体系统的表达式。多体的情况可以以此类推。少许文献只是在形式上涉及非相对论量子系统的多体情况[13,14]。有的文献还讨论量子统计系综的维里定理[15,16]。这时会涉及到温度。本文不讨论涉及温度的情况。 克劳修斯最先提出了维里这个物理量。维里的定义如下:一个粒子在运动时,把它的位矢和动量的点乘定义为这个粒子的维里。 G=r·p (2a) 如果一个系统有不止一个粒子,就把所有粒子的维里求和,定义为这个系统的‘总的维里’。 (2b) 经典力学的维里定理:一个系统在稳定运动时,维里对于时间的导数的时间平均值为零。表达式为 (3) 如果该运动是周期运动,那么在一个运动周期内对时间取平均。 维里对于时间的导数为 (4) 其中用到了牛顿第二定律。 以下,我们要把速度和动量之间的关系式代入。对于低动量运动和相对论运动,速度的表达式是不同的。因此,需要分别考虑。本文总是同时考虑正动能和负动能物质运动的公式[20]。 一个物体的速度和动量之间的关系如下[20]。 (5) 其中,正负号分别表示正动能和负动能物质的运动。由此可知, (6) 式中,T为动能。这表明式(4)右边的第一项是系统总动能的2倍。稳定运动时,该物体所受的作用力写成势能的负梯度。 (7) 由式(3)-(7),得到 (8) 以下我们来看最简单的一个物体和两个物体的情况。 若只有一个物体,它在势场V中运动,那么,式(8)就简化为 (9) 此式既包含了正动能的情况,也包含了负动能的情况。我们说,是关于正负动能对称的。 设势能与距离的一次方成反比,如: (10) 式中,a是常数。这样的势,对应着平方反比力。当a<0时,为吸引势,对应着吸引力;当a>0时,为排斥势,对应着排斥力。那么,式(9)就简化为 (11) 此式表明,动能平均值的2倍是势能平均值的负值。通常,大家以此作为维里定理的结论。实际上,这是粒子受到平方反比力的作用而做稳定运动时的结论。 从式(11)可知,当a<0时,为吸引势能,其动能必为正。当a>0时,为排斥势能。其动能必为负。 再来看另一个例子。设物体仅受到一个弹性力的作用。其弹性势能是 (12) 式中,b是一个常数。当b>0时,对应着弹性回复力;当b<0时,对应着线性排斥力,这是一个排斥势能。那么式(9)就写成 (13) 经典理论中,物体做简谐运动。简谐运动的平均动能和平均势能的符号相同,数值相等。如果一个物体具有正动能,它就只能在弹性回复力的作用下做稳定运动。如果一个物体具有负动能,它只能在线性排斥力的作用下做稳定运动。 式(11)和(13)表明,在不同的势能中,物体的平均动能的符号可能与平均势能的符号相反,也可能相同。但是两者有一个共同点,就是:正动能物体,只有受到吸引力的作用,才能做稳定运动;而负动能的物体,只有受到排斥力的作用,才能做稳定运动。这就是式(9)反映的物理内容。 在经典力学中,一个物体能否做稳定运动,判据是维里定理。一个物体受到吸引力,做稳定的运动。如果一个物体受到排斥力,不可能做稳定运动,但是这一结论只对正动能的物体适用。本文的讨论包括了负动能的情况。上述公式表明:负动能的物体受排斥力的作用,也可以做稳定运动。 若势能在无限远处为0,即把无限远处定位势能零点,那么,动能为正(负)的稳定系统,总能量一定是负(正)的。 根据经典理论,一个正动能物体做稳定运动,它的总能量必然达到极小值[8]。对于负动能物体做稳定运动的情况,笔者在文献[19]中证明其总能量应该达到极大值。 常见的几种形式的势能可写为V(r)∝rn。这里,我们只讨论式(10)和(12)形式的势能,即n=-1和n=2。这两种形式的物理意义最为明确。 下面以两个物体组成的系统为例,进行讨论。假定两个物体之间的作用势能是V(r1-r2),那么两个物体受到的作用力分别为 (14) 式(6)和(14)代入式(4),得到维里定理表达式为 (15) 通常,两个相互作用的物体,在合适的条件下,可构成一个稳定的系统,如“地—月系统”。但这是经典力学中,两个物体都为正动能的例子。由式(15)可知,两个物体组成稳定的系统共有四种的情况。在文献[20]中,假定两物体之间是平方反比力,给出来这四种稳定运动的图像。四种情况都符合维里定理(15)。总动能都是势能负值的一半,其中两种情况的总动能为正。只有在相互吸引的作用力下才能有稳定的运动,并且系统的总能量达到极小,是个负值。对于总动能为负的情况,只有在相互排斥的作用力下才能达到稳定运动,并且系统的总能量达到极大,是个正值。 由式(15)可知,每个物体都可能有“正”或“负”动能,由两个物体组成稳定系统,就有四种可能性。以此类推,N个物体组成稳定的系统有2N种可能性。 相对论性速度与动量之间关系如下[20], (16) 式(6)就改为 (17) 注意,把相对论的表达式(17)与低动量表达式(6)区别开来。式(17)并不是相对论动能的2倍。自由物体相对论动能的表达式是 (18) 如果动量很低(cp≪mc2),可做近似处理(m2c4+c2p2≈m2c4),那么,式(17)就简化为非相对论动能的2倍,见式(6)。极端相对论的情况,可做近似处理(mc2≪cp),式(17)写为v·p=±cp。 式(17)和(7)代入式(4),就得到相对论的维里定理,如下: (19) 若是一个物体的运动,则等式两边都只有一项。 (20) 其中,正负号仍然表示正负动能的情况,体现了维里定理关于正负动能的对称性。对于式(20)的物理分析与非相对论式(9)一样。正(负)动能的物体,只有受到一个吸引(排斥)势的时候,才能有稳定运动。 对于两个物体的系统,式(19)式的左边有两项,每一项都有正负两个符号,与式(15)左边类似。讨论过程也是类似的。 在量子力学中,力学量必须用算符表示。因此,现在式(2)是维里算符。要计算维里的量,就是计算维里算符在波函数中的平均值,记为〈G〉。对于稳定运动,就是定态波函数。 量子力学的维里定理:维里在定态波函数中的平均值对时间的全微分为零。已知系统的哈密顿量为H。那么,维里定理的表达式就是 (21) 表面上,式(21)没有像式(4)一样将维里对时间平均。文献[10]中也给出了表达式(21),但没有推导过程。实际上,式(21)也是由式(3)推导而来的。这一点,还没有人直接证明过。现在来证明这一点。先写出维里对于时间的全导数。 (22) 维里定理要求式(22)对时间的平均为零。维里算符G本身是不显含时间的。定态波函数随时间变化的关系就体现在因子e-iωt上[10-12]。这个因子表明定态一定是个时间周期函数。又因为e-iωt对一个周期的时间平均为零,式(22)第一项对于时间的平均值为零。第二项不含时间,不用写出其对时间的平均值。因此,量子力学的维里定理就简化为式(21)。 根据各种具体的哈密顿量,可以计算其对易关系。 哈密顿量是 (23) 式(23)包括了正负动能的两种情况。为计算式(21),需要做对易关系 (24) (25) 维里定理表示成 (26) 对比式(8)与式(26)可知,将前者对时间的平均改写为对定态的平均,就成为后者。 先考虑一个粒子的情况。 若势能是式(10)的库仑势,代入式(26),就得到 (27) 式(27)与式(11)相同,只是把时间平均写成了定态平均。 若势能是式(12)的谐振子势,代入式(26)得 (28) 也是将式(13)中的时间平均写成定态平均,即得(28)。 注意,在量子力学的情况,在式(10)中a<0(a>0)表示势阱(势垒);式(12)中的b<0(b>0)表示势阱(势垒)。因此,量子力学中的结论是:一个正(负)动能粒子只有在势阱(势垒)中运动,才是稳定的。这与经典力学的结论实质上是相同的,只是用了量子力学的语言。 我们由此得到一个结论:如果宇宙中负动能粒子之间只有万有引力作用,它们一定是均匀弥散在宇宙空间的。现在一般认为,暗物质是弥散在宇宙空间中的。这暗示了暗物质有可能就是负动能物质。 若是由两个粒子组成的系统,它们之间的相互作用势是V(r1-r2),那么,维里定理(21)的具体表达式就是 (29) 其中,每一个粒子分别可以是正负动能两种情况。式(29)左边共有四种情况。此式的分析与(15)是相同的。 我们知道,电子带负电荷,质子带正电荷。它们的反粒子分别带相反的电荷。氢原子是一个正动能电子和一个正动能质子依靠它们之间库仑吸引势构成的稳定系统。同样,一个正动能正电子和一个正动能反质子依靠它们之间库仑吸引势构成稳定的系统,这是反氢原子。我们把正反氢原子概括在同一句话中:一个正动能电子(正电子)和一个正动能质子(反质子)依靠它们之间库仑吸引势构成的稳定系统,就是氢原子(反氢原子)。我们在前面的工作中列出了另外三种可能的稳定系统[20]。它们分别是:一个负动能正电子(电子)和一个负动能质子(反质子)依靠它们之间库仑排斥势构成的稳定系统,叫做暗氢原子(反暗氢原子);一个正动能电子(正电子)和一个负动能质子(反质子)依靠它们之间库仑吸引势构成的稳定系统,叫做混氢原子(反混氢原子);一个负动能电子(正电子)和一个正动能反质子(质子)依靠它们之间库仑排斥势构成的稳定系统,叫做暗混氢原子(反暗混氢原子)。这是式(29)所表现的四种情况的具体应用。作者[20]建议在天体光谱中寻找混氢原子的谱线,它们相对于氢原子的谱线是蓝移的。 作为一个实际的应用,作者指出,由于处于势垒中的电子具有负动能,两个这样的电子可以依靠它们之间的库仑排斥作用而成为一个稳定的二体系统[17]。这很可能是固体材料中电子配对的一个新的机制。 哈密顿量要用分解的克莱因—高登哈密顿量的形式[20]。 (30) 代入维里定理(21),经计算对易关系,维里定理就成为: (31) 此式也只要把式(19)的时间平均写成在定态中的平均即可。因此,分析过程与式(19)一样。 量子力学中非相对论粒子和自旋为0的相对论粒子都有经典对应。具体体现为:在经典力学的维里定理的具体表达式中,把有关物理量对时间的平均写成对于定态的平均,即成为量子力学的维里定理的表达式。 自旋为1/2的相对论性粒子,因为其波函数是用旋量来表示的,是没有经典对应的。经典粒子没有自旋这个物理量。讨论维里定理仍然是式(21)。 一个自旋为1/2的粒子服从狄拉克方程。两个粒子的运动则服从二粒子狄拉克方程。多粒子的运动方程更复杂,本文不讨论。我们只讨论单个粒子和两个粒子的系统的维里定理。 一个粒子的狄拉克哈密顿量是 H=cα·p+mc2β+V (32) 其中 (33) 其中σ是泡利矩阵。可以计算得到如下的对易关系。 [r·p,σ·p]=σ·p (34) [r·p,α·p]=α·p (35) 将哈密顿量式(32)代入维里定理(21)。利用式(35)计算对易关系,维里定理就成为: (36) 前文中,维里定理的具体表达式的左边,包括了正负动能的情况。式(33)左边没有明确写出正负动能,但实际上都已经被包含在其中。这是因为哈密顿量(32)的定态方程,既有正动能解也有负动能解。 我们把定态方程写出来 (cα·p+mc2β+V)Ψ=EΨ (37) 把波函数写成二分量旋量的形式 (38) 其中,φ和χ各都是二分量旋量。方程(37)式有四个解,其中两个属于正动能E(+),两个属于负动能E(-)。自由粒子的能量就是式(1)。在正动能解中,φ是大分量而χ是小分量[10,21];在负动能解中,φ是小分量而χ是大小分量。负动能解的特点以前没有人分析过。作者在文献[17]中第一次详细分析了负动能解。如果矢量α反号,α⟺-α,那么,式(36)的正负能解的本征值和相应的本征函数交换,即E(+)⟺E(-),φ⟺χ。这就是在引言中提到的狄拉克方程的第三种对称性。因此,式(36)中已经自动地把正负动能的情况都包括进去了。 为了展示这一点,本文做了低动量近似。式(36)采用式(38)的波函数。再将式(33)代入维里定理得 (39a) (39b) 对于正动能解E(+)>0,φ是大分量而χ是小分量。做低动量近似时,它们之间有如下关系式[21]: (40) 代入式(39a),得到 (41) 该粒子是在一个势场中运动的,而能量E(+)中还含有相互作用能的部分,并不是自由粒子的形式。因此,式(41)的左边就不是真正的动能。式(41)与(31)左边不同,原因是自旋1/2的粒子没有经典粒子对应。而自旋为0的粒子是有经典粒子对应。式(41)是正动能解,稳态粒子的总能量达到极小值。 对于负动能解E(-)=-E(+)<0,φ是分量而χ是大分量。实际上,正负能解具有对称性[17]。做低动量近似时,关系式如下: (42) 代入式(39b),得到 (43) 这是负动能解的情况,所以总能量达到极大值。 因此,在低动量近似时,维里定理正负动能的具体表达式分别为(41)式和(43)式,可以把两式统一写成: (44) 注意,取正号时,应在φ态中求平均;取负号时,应在χ态中求平均。 式(40)~(44)是低动量近似的情况,正负动能解可以分开来计算。任意动量的情况只能用原式(36)计算。正负动能解之间是有耦合的,见式(39)。这种形式无法把正负动能区分开来。 二粒子狄拉克方程的哈密顿量已经给出[22-24]。狄拉克方程提出来之后,人们就想到要对相互作用的两个粒子做细致的研究,提出了对二粒子狄拉克方程做低动量近似的方法[25,26]。这是从单粒子狄拉克方程的低动量近似方法[27]发展而来的。可是,由于人们很快就用量子场论的方法来处理基本粒子的相对论运动,认为实用的目的达到了,就不再继续对于二粒子狄拉克方程做透彻的研究。作者秉持在引言中所说的四个基本观点,认为二粒子狄拉克方程是一个正确的方程,对其做低动量近似,可以得到低动量时二粒子系统的所有性质,这将探究出多粒子系统更多特性。为简化模型,本文只探讨二粒子系统的维里定理,其表达式基本公式仍然是式(21)。 先回顾一个粒子的狄拉克哈密顿量。它是四阶的,这是因为,粒子的能量可有正负两个解,每个解可以有自旋上下两个状态。因此,波函数必须是四分量的。哈密顿量就是四阶矩阵。 考虑两个粒子组成一个系统的情况。对于自由粒子,每个粒子都有正负能量之分,见式(1),两个粒子按正负能量组合,就有四种。同时,每个粒子的自旋又分“上、下”,两个粒子的自旋也有四种,分别是“上上、下下、上下、下上”。若既考虑正负能量又考虑自旋状态,将有16种组合。因此,波函数必须是16分量的旋量。相应地,哈密顿量就是16阶矩阵。以此类推,N个粒子的系统的波函数应该是4N分量的旋量。 现在考虑两个粒子之间有相互作用势V(r1-r2)而组成的系统。此处把这个哈密顿量H(1,2)它尽可能简略地写在下面。 (45) 其中,H(0)是如下的8阶矩阵。 (46) 我们记 a1=cσ·p1,a2=cσ·p2 (47) (48) 在矩阵H(0)中,每一个元都是一个二阶矩阵。泡利矩阵σ是二阶矩阵。 式(45)中的两个矩阵H(0)的本征值是相同的。但是它们的自旋构型不同,各有两个自旋构型。式(45)中的上H(0)矩阵,两个粒子的自旋可以是“上上”或“下下”;下H(0)矩阵,两个自旋则是“上下”或“下上”。本文只考虑哈密顿量与自旋无关的情况,因此我们不考虑自旋构型。只需研究其中一个H(0)八阶矩阵,其波函数也是八分量旋量。不含时的定态波函数记为 Φ=(Φ1Φ2Φ3Φ4)T (49) 式中,上标T表示对矩阵的转置。式(49)中,每一个分量又都是二分量旋量。 现在将哈密顿量(46)-(48)式代入(21)式。计算对易关系时,用到式(34)。维里定理的具体表达式为: (50) 式(50)的右边与式(29)的右边形式相同,都只有对角元,容易计算。式(50)的左边则较为复杂。为了给出其物理含义,本文仿照单粒子的情况,做低动量近似,即指系统的总能量E满足 E≪m1c2,E≪m2c2 (51) 先写出含时方程 (52) 因为此处哈密顿量不含时间,所以式(51)中的波函数Ψ和式(49)中的不含时波函数Φ之间只差一个时间相因子。但是,时间相因子的选取与两个粒子的正负动能有关。做低动量近似时,需要判断波函数中的大分量和小分量。而大小分量的判断依赖与两个粒子的正负动能有关。两个粒子的正负动能的组合共有四种情况,要根据每一种情况分别选取合适的时间因子。 (1) 设两个粒子都具有正动能。做如下变换 Ψ=Φe-i[E+(m1+m2)c2]t/ћ (53) 联立式(49),(52)和(53)得: (54) 将后三个方程写成如下形式。 (55a) (55b) (55c) 现在将式(55c)代入式(55a)和(55b)。由于式(55c),可以看到式(55a)和式(55b)的第二项都是小量,可略去,所以,它们就近似成 (56a) (56b) 可见,此种情况下,Φ1是大分量,与Φ1相比,Φ2和Φ3是一级小分量,Φ4则是二级小分量。因此,在式(50)左边,第三、四、七、八项可去掉。即只保留带有Φ1的四项。用(56a)代入,就得到 (57) (2) 粒子1负动能粒子2正动能。做如下变换 Ψ=Φe-i[E-(m1-m2)c2]t/ћ (58) 由式(49)、(52)和(58)得到分量所满足的方程组。分析过程同上。此时,Φ2是大分量,与Φ2相比,Φ1和Φ4是一级小分量,Φ3则是二级小分量。因此,在式(50)左边,第三、四、五、六项可去掉。只保留带有Φ2的四项,就得到 (59) (3) 粒子1正动能粒子2负动能。做变换 Ψ=Φe-i[E+(m1-m2)c2]t/ћ (60) 由式(49),(52)和(60)得到分量所满足的方程组。分析过程同上。此时,Φ3是大分量。与Φ3相比,Φ1和Φ4是一级小分量,Φ2则是二级小分量。因此,在式(50)左边,第一、二、七、八项可去掉。只保留带有Φ3的四项,就得到 (61) (4) 两个粒子都具有负动能。做如下变换 Ψ=Φe-i[E-(m1+m2)c2]t/ћ (62) 由式(49)、(52)和(62)得到分量所满足的方程组。分析过程同上。此时,Φ4是大分量,与Φ4相比,Φ2和Φ3是一级小分量,Φ1则是二级小分量。因此,在式(50)左边,第一、二、五、六项可去掉。只保留带有Φ4的四项,就得到 (63) 式(57)、(59)、(61)和(63)是在满足式(51)条件下的近似表达式,可以只在一个分量中求平均值,并且当分母中的E完全略去时,就成为非相对论的式(29)。对于一般情况,必须用原式(50)做计算,各分量之间是有耦合的。以上只计算了式(46)中上H(0)矩阵的矩阵元。对于下H(0)的计算结果完全相同。因此,要把式(57)、(59)、(61)和(63)这四式都乘以2。将此四式前的因子都改为4。因为每一种能量有四种自旋组合,而此处哈密顿量与自旋无关,这四种自旋组合的贡献是相同的。 本文把四种情况下四个分量的相对大小列表,见表1。对于单粒子情况,波函数分为大小分量。对于二粒子情况,有大分量和一级与二级小分量。由此推想,若是三粒子系统,波函数的分量应该分为大分量,一级二级和三级小分量。 表1 相对论自旋1/2的二粒子系统的大分量和小分量 (1) 本文对于维里定理做了全面的研究。从统一的公式出发来写出维里定理,即物质做稳定运动时,维里随时间的平均值为零。对于量子力学的情况,维里的量就是维里算符在定态波函数中的平均值。对于经典力学和量子力学的各种情况,都写出了维里定理的具体表达式。这些情况是:非相对论和相对论运动,单体和二体系统。对于自旋为1/2的系统做了详细的讨论,给出了低动量近似下的表达式。 (2) 引言提到量子力学方程有三个对称性。本文表达的维里定理体现了第四种对称性:维里定理关于正负动能的对称性。对于经典力学和相对论力学,对于非相对论运动和相对论运动,都有同样的对称性。这就是与引言中所说的基本观点一致:如果相对论运动具有一种对称性,这种对称性在低动量运动中仍然是保留的,不会丢失。这反映了我们宇宙关于正负动能物质运动的对称性。 (3) 一个粒子或者物体是否能够做稳定运动的最终判据是维里定理。根据维里定理,一个正(负)动能的粒子或者物体,只有在受到吸引(排斥)作用时,才有可能做稳定运动。 (4) 本文提到的负动能物质的来源,既是对于狄拉克方程负动能解的正确理解,也是理论上对称性的要求,负动能的物理实在性有待实验验证。1 经典力学的维里定理
1.1 非相对论运动


1.2 相对论运动
2 量子力学的维里定理
2.1 非相对论粒子


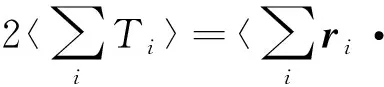

2.2 自旋为0的相对论粒子

3 自旋为1/2的相对论粒子
3.1 一个粒子的情况
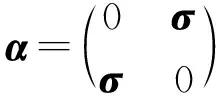







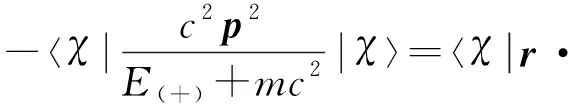
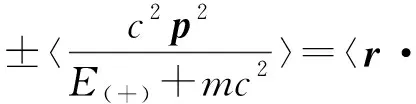
3.2 两个粒子的情况
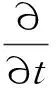
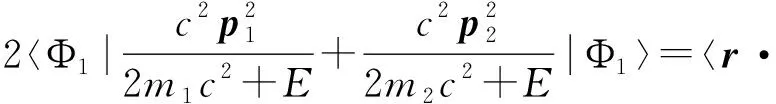


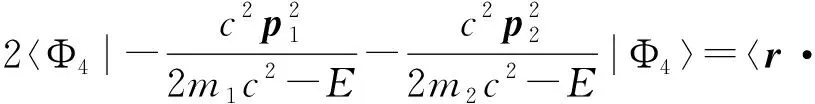

4 结论

