Numerical simulation of the effects of protrusion on DC arc anode attachment

Chong NIU (牛冲), Xian MENG (孟显), Heji HUANG (黄河激),Tao ZHU (朱涛), Surong SUN (孙素蓉),3,∗and Haixing WANG (王海兴),3,∗

1 School of Astronautics, Beihang University, Beijing 100191, People’s Republic of China

2 Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, People’s Republic of China

3 Ningbo Institute of Technology, Beihang University, Ningbo 315800, People’s Republic of China

Abstract The attachment of the DC arc on the anode is usually affected by surface morphology such as protrusions due to ablation or melting deformation.A three-dimensional thermodynamic and chemical non-equilibrium model is used to numerically simulate the effect of artificially assumed surface protrusions on the arc anode attachment.The numerical simulation results show that the arc deflects toward the protrusions on the anode and attaches to them in a constricted mode,resulting in an increase in the temperature of the arc attachment region.The analysis shows that the presence of protrusion on the anode surface changes the electric field distribution,intensifies the degree of thermodynamic and chemical non-equilibrium in its vicinity,further influences the chemical kinetic process of the plasma around it, which is the main reason for the deflection of the arc toward the protrusions and the arc anode attachment in a constricted mode.In order to verify the numerical simulation results,verification experiments are also performed using similar size scale anode protrusion, and the results showed that the presence of protrusion can indeed cause the deflection of the arc and even cause the ablation of the protrusion.

Keywords: DC arc, arc anode attachment, anode protrusion, chemical non-equilibrium

1.Introduction

The anodes of the DC arc devices used in the fields of electric propulsion and material processing are often subjected to high current and heat flow fluxes.In the case of extremely high heat flux or insufficient cooling, the anode suffers noticeable damage at the attachment region, especially for the constricted arc attachment mode.The temperature of the arc anode attachment region continues to rise, which may cause deformation, melting, and even ablation of the anode surface to form some structures with different sizes, such as protrusions or craters.These protrusions or craters have important effects on the arc anode attachment,causing the arc parameter distribution lose symmetry and even stability.Although there have been intensive investigations on the anode phenomena of DC arc which are related to the anode-plasma interaction,such as the physics of anode spots [1–5] and arc attachment mode [6–9], most studies are based on the assumption of a smooth anode surface.Our understanding on the effects of anode morphology on the arc attachment mode is still inadequate, mainly due to the complicated interaction mechanisms of the arc plasma and anode involved.

Previous studies have shown that surface morphology of the electrodes, such as bumps, burrs, roughness, etc, has substantial influence on the mode of electrode arc attachment,while most of the studies focused to the interaction between the cathode and the arc [10–12].In the field of vacuum arc research, the effect of the protrusion on the cathode surface has attracted wide attention, which is because the protrusion plays an important role in the arc spot formation and evolution [13, 14].Actually, the effect of protrusions on the DC arc attachment on the anode surface is also important which is closely related to the ablation of anode.Since the protrusions are inside the anode boundary layer which is characterized by large gradients of the plasma parameters,so it is very difficult to analyze and study their effect on arc attachment.Therefore,the development of numerical simulation approach is important to investigate this process.As demonstrated in previous studies [15–19],at the arc fringes and inside the arc anode boundary layer, the plasma deviates significantly from the thermodynamic and chemical equilibrium [20–30].Therefore thermodynamic and chemical non-equilibrium should be important features of the region near the anode protrusions and should be considered in the physical model.A reasonable chemical kinetic model should be used to simulate the effect of protrusions on arc anode attachment[31–35].

The main purpose of this paper is to provide a preliminary understanding of the influence of protrusions on arc anode attachment.An artificially assumed millimeter-level protrusion on the anode surface is adopted to study the influence of the protrusion on the arc attachment.In the study,the anode solid zone is also coupled to computational domain,allowing to obtain the temperature distribution of anode protrusion.Numerical simulation results of the effect of protrusions on arc anode attachment are presented, followed by preliminary experimental validation.

2.Modeling approach

2.1.Computation domain

Figure 1 shows the schematic diagram of the wall-stabilized transferred arc device used in the calculation.The length and radius of the water-cooled constrictor tube are 40 mm and 5 mm, respectively, which are the same sizes with the experimental setup in[36].The distance between the outlet of the water-cooled constrictor tube and the anode surface is 12 mm,the radius of the anode is 15 mm,and the thickness of the anode is 10 mm.The cathode is assumed to be a round rod with a radius of 2 mm, with a top cone angle of 60°, and a small platform with a radius of 0.5 mm.In this study, we artificially set a trapezoidal protrusion on the anode surface.The radii of the bottom and the top of the protrusion are 0.5 mm and 0.2 mm,and the height is 1 mm.Considering that the protrusion of the anode surface may cause the arc to lose axi-symmetry,three-dimensional simulation is adopted in this study.Since the arc and the device are symmetric about theyz-plane (x=0 mm), ABCDEFGHIJ in the figure 1 is set as computational domain, which is the half of the arc device in this simulation.In this simulation,the governing equations of arc plasma and anode region are solved together.

Figure 1.Schematic diagram of wall-stabilized transferred arc setup and computational domain used in calculation.

Figure 2.Comparison between the calculated electron temperature (lines) and the experimental data (symbols).

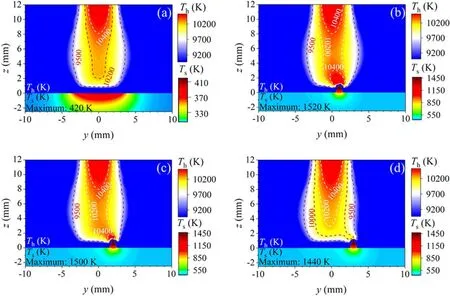
Figure 3.Heavy-species temperature distributions for the cases without(a)and with protrusion at different radial positions.(b)y=1 mm,(c)y=2 mm, (d) y=3 mm.

Figure 4.Temperature distributions for the cases without and with protrusion at the radial position y=2 mm.

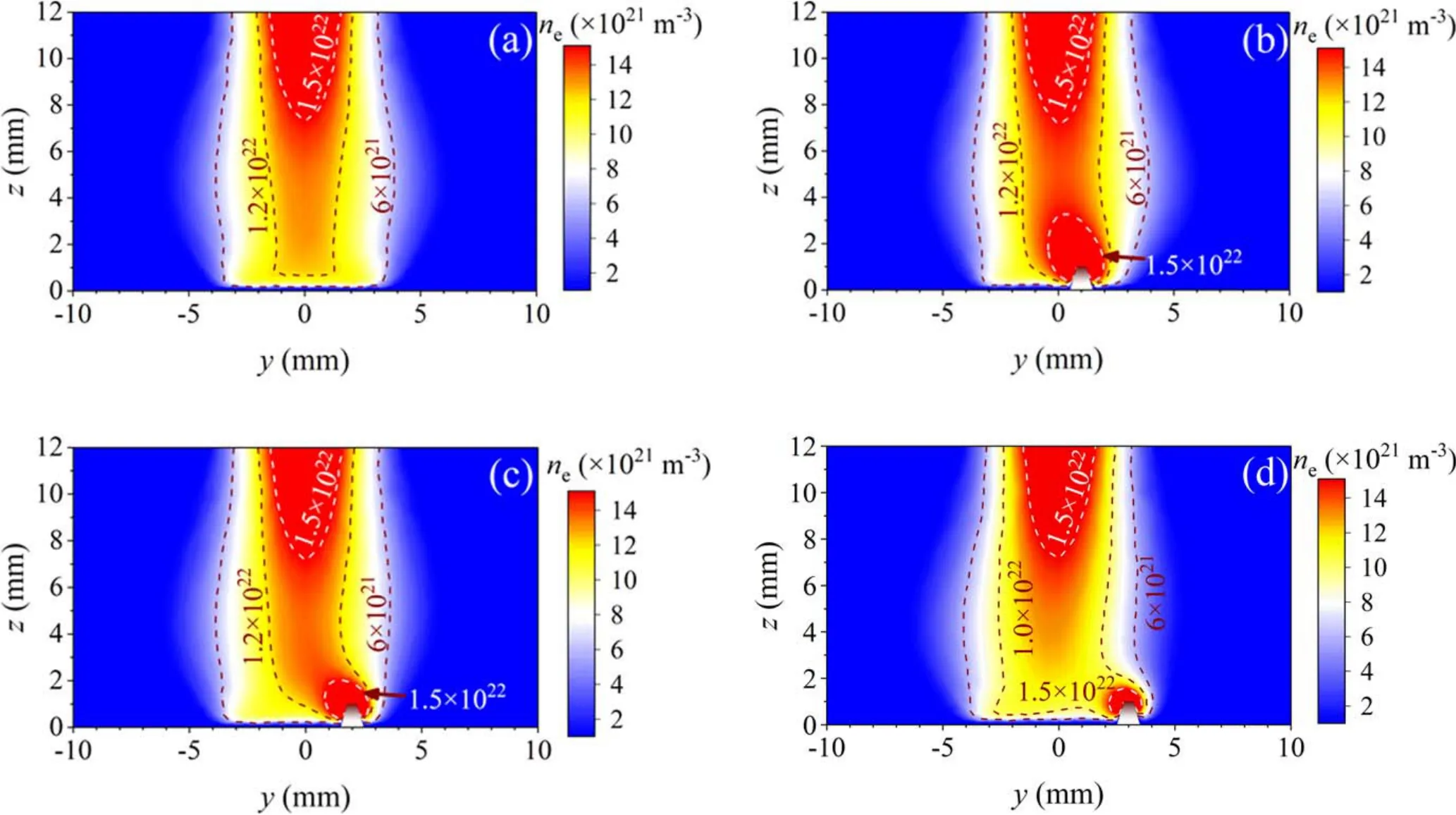
Figure 5.Electron number density distributions for the cases without(a)and with protrusion at different radial positions.(b)y=1 mm,(c)y=2 mm, (d) y=3 mm.

2.2.Main assumptions and governing equations

The following assumptions are used in this simulation.(1)The flow is considered as steady and laminar.(2) The arc anode is operated without ablation, even if it is considered that the artificially set protrusion may be heated to a higher temperature.(3) Arc plasma is electrically neutral, and the radiation loss is evaluated by net emission coefficient with absorption radiusR=0 mm.(4) The thermodynamic nonequilibrium chemical non-equilibrium are considered, and a five-species (ground state atoms, excited state atoms, atomic ions,molecular ions and electrons)is include in the chemical kinetic model.

Based on the above assumptions, the required governing equations are as follows.

Gas species equation

Here,ρsandare the mass density and diffusion flux of speciess.In this simulation,the diffusion fluxis calculated by the self-consistent effective binary diffusion approximation developed by Ramshaw [37–39].Sc,sis the chemical reaction source term which is determined by different kinetic processes shown in table 1.The diffusion flux→are obtained from equation (2) [40, 41].Here,pis the gas pressure.Msis the molecular weight andDsis effective diffusion coefficient.This the heavy-species temperature solved by heavy-species energy equation.Rgis the universal gas constant andysis the mass fraction of speciess.is the volumetric driving force defined asHere,qsis the charge per unit mass of speciessandis the ambipolar diffusion electric field.→is the driving force shown in equation (3)whereis the partial pressure of speciess,andβsjis the thermal diffusion coefficient between speciessandj

Table 1.The reactions taken into account in the numerical model.

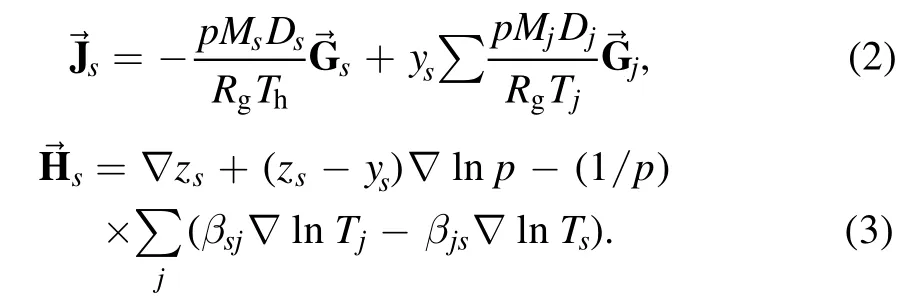
Momentum conservation equation

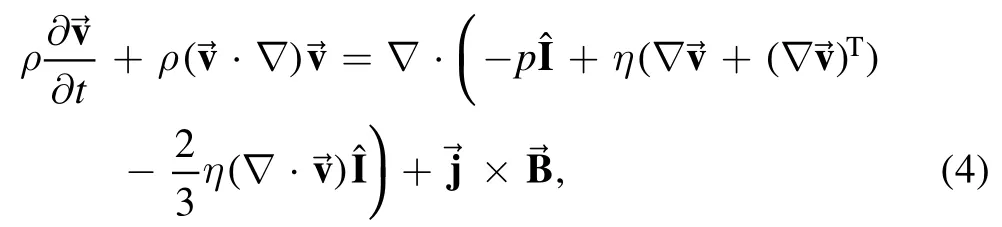
Current continuity and Maxwell’s equation

whereμ0is the the permeability.

The electrical conductivity is given by equation (7).Here,ecis the elementary charge.neandmeare number density and mass of electron respectively.vmis the sum of collision frequencies between electrons and heavy-species including the atoms and ions

Electron energy equation

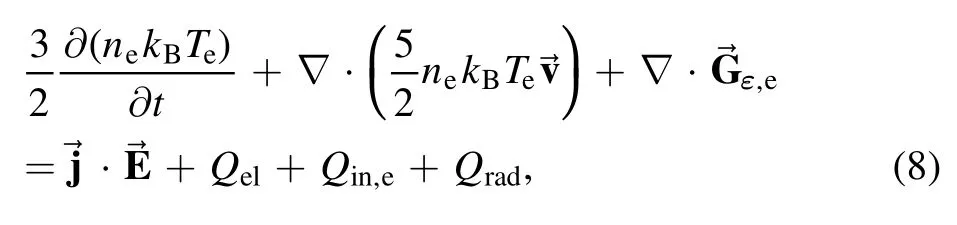
whereTeandkBare respectively the electron temperature and Boltzmann constant.is the electron energy flux density,which can be expressed as follows

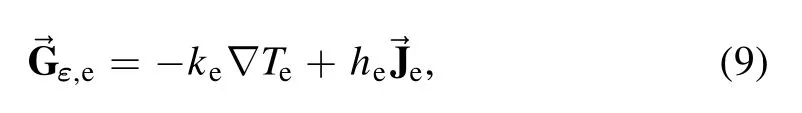
wherekeis the electron thermal conductivity,heis the specific enthalpy of electron and→is the diffusion flux of electron which can be calculated by relation[35].In the right-hand of equation (8),represents the Joule heating andis the electric field which is calculated by relationφ= ∇,here,φis the electric potential.Q,elQin,eare respectively the electron elastic collision term and the reaction heat due to electron impact reactions,which can be calculated by

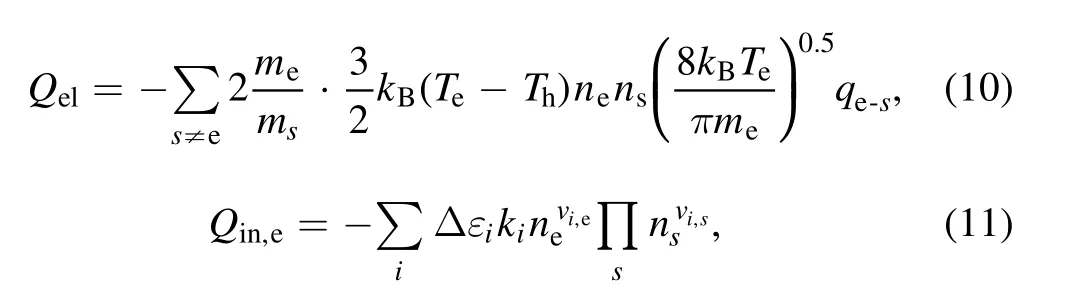
whereqe‐srepresents the cross sections for collisions between electrons and heavy-species, which are obtained from [49].Δε iis the energy loss due to inelastic collisions which is related to the corresponding kinetic process.vi,srepresents the stoichiometric coefficients corresponding to speciessin reactioni.In equation(8),Qradis net radiation losses obtained from [50].

Table 2.The boundary conditions of the numerical model.

Heavy-species energy equation

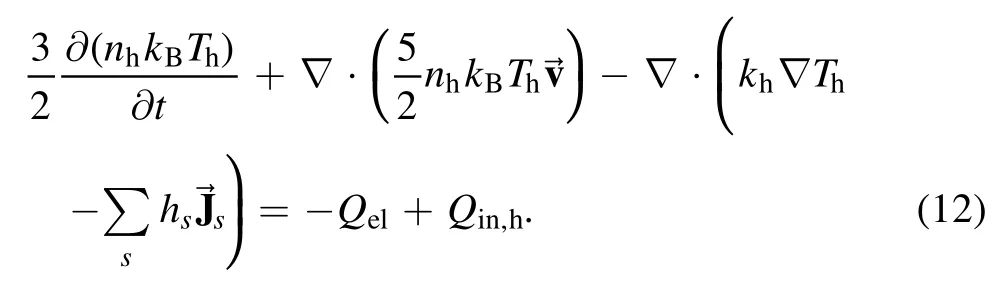
Here,nhandkhare respectively the number density and the thermal conductivity of heavy-species.hsand represent the species specific enthalpy.Qin,his the reaction heat due to heavy-species impact reactions.

In this paper, five-species are considered in the model.The excited state atoms (Ar*), molecular ions (Ar2+), and atomic ions (Ar+) are obtained from species equation.The electron density is determined by the charge neutrality condition,The density of ground state atom(Ar) is calculated by state equation.

Since in this simulation, the copper is chosen as anode material.The anode is coupled to plasma region and its energy equation is as follows

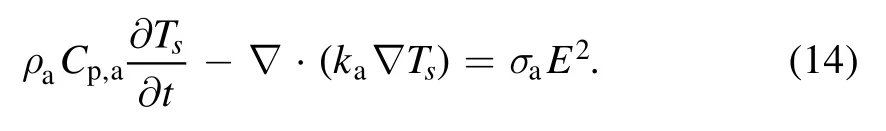
Here,Tsis the temperature of the solid anode.ρa,Cp,a,kaandσaare the density,specific heat,thermal conductivity and electrical conductivity in copper anode, the data are obtained from [51].

Thermodynamic and transport properties involved in the previous governing equations are important for obtaining reasonable arc parameters and distributions, especially in the region with large parameter gradients.In this paper, these properties are calculated based on the temperature and species number density of the grid nodes during each iteration.The calculation methods of thermodynamic and transport properties of plasma under non-equilibrium conditions can be found in [52–54].The transport properties are calculated based on the Chapman–Enskog method,in which the collision between the particles is evaluated by collision integral.The collision integral can be obtained by integrating the interaction potential between particles.The collision integrals between neutral particles are calculated by HFDTCS2 potential [55],and the interaction potential of ions and neutral particles is obtained from [56].The Coulomb potential is used for the calculation of collision integral between charged particles,and the collision integrals of electrons and neutral particles are obtained from [57].

2.3.Boundary conditions

The boundary conditions used in the calculation are shown in table 2.The gas enters from the annular channel between the inner wall of the constrictor and the outer wall of the cathode with flow rate of 0.35 slpm.The gas flows out from the gap between the bottom wall of the constrictor and the anode surface and the pressure is set as 1 atm at outlet.Non-slip flow conditions are set at the walls of water-cooled constrictor and the anode surface.

For heavy-species temperature,the gas temperature is set as 300 K at the inlet, outlet and inner and bottom walls of constrictor.Along the cathode surface, the temperature is assumed to gradually change from 300 K at the rod part to 3500 K at the cathode flat tip.The anode bottom is watercooled,and its temperature is set to be 300 K,while the upper surface of anode is coupled to the arc plasma and its temperature can be obtained self-consistently.For the electron temperature, it is set to be 300 K at the inlet.At other boundaries, zero electron temperature gradient is adopted.

For anode,several important heat transfer processes,such as electron condensation heat, electron enthalpy transport,conduction heat and radiation loss are taken into account[23,51,58,59].The conduction heat transfer between the arc plasma and anode is solved by coupling.Therefore, the boundary conditions of anode heat transfer in this model can be set as follow:

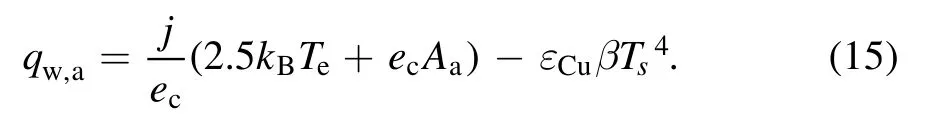
Here, the first term is the electron enthalpy transport and the electron condensation heat, and the second term is the anode radiation loss.Aa,εCuandβare respectively the work function, surface emissivity and Stefan–Boltzmann constant,which are taken from [51].

At the cathode surface, the current density is assumed to be a Gaussian distribution as in [60], the peak value ofjmax=3.0×107A m−2is chosen forI=50 A.At the anode,the electric potential on the bottom surface of anode is connected to ground.Electric insulation is adopted along the other boundaries.For the magnetic vector potential equation, the Dirichlet boundaries are set at inlet, outlet and the walls of constrictor tube, and zero gradients are adopted at other boundaries.For species equation, zero gradients are set at all boundaries.

It is expected that the presence of protrusion would lead to the ablation of the copper at the tip of protrusion,and then the copper vapor would enter the plasma zone.Therefore it is necessary to properly consider the effects of copper vapor on the plasma properties near the protrusion, especially the electrical conductivity.A more reasonable method is to develop a reasonable chemical non-equilibrium kinetic model that includes the mixing of metallic copper vapor and its ionization process with argon plasma.However,this is a very challenging task.In this simulation, we use a method similar to previous literatures[61,62]to improve the conductivity of the boundary layer.In this simulation, an artificially high electrical conductivity of a mixture of 50%Ar and 50%Cu is used to increase the conductivity of the boundary layer within the thickness of 0.2 mm around the protrusion.The electrical conductivity of the Ar–Cu mixture is calculated based on the Chapman–Enskog method, and the collision integrals required for the calculation are obtained from the [63].

A non-uniform mesh with 30 (x-direction) × 56 (y-direction) × 94 (z-direction) is used in the simulation, and a refined grid is adopted near the electrodes, especially around the protrusion region of the anode surface.The parameter distributions are the same compared with those calculated by finer mesh so that the numerical results do not depend on grid accuracy.For decrease of computational effort,therefore,the mesh with 30(xdirection) × 56 (y-direction) × 94 (z-direction) is used.The complete set of coupled governing equations listed above is solved based on the COMSOL software platform [64].

3.Results and discussion

3.1.Comparison and verification of numerical simulation results and experimental measurement results

To verify the reliability of code in this simulation, we compared the calculated results with the experimental results reported in [36] based on the same conditions.The anode region of arc with a superimposed cold flow was investigated in[36]for the wall-stabilized arc device shown in figure 1.In[36], three-dimensional electron temperature distributions are obtained with a laser Thomson scattering system,for the case with arc current of 100 A and the argon flow rate of 5 slpm,and cross flow rate of 12 slpm.

From the comparison of the calculated electron temperature and the experimental measurement results given in figure 2,it can be seen that the calculated temperatures are in good agreement with the experimental results.However, in the upstream region of the lateral gas flow,which is the region with a larger parameter gradient,the numerical results deviate from the experimental data.The temperature gradients of experimental data are steep, while the gradients at the same position are underestimated by the numerical model.The predicted results of the same numerical approach are also compared with the experimental results presented in [65], as shown in [40].Generally, the results of numerical simulation predictions are acceptable in this simulation.

3.2.Effects of the existence of protrusion on arc temperature and electron number density distributions

In this section, the effects of protrusion on temperature and electron number density are discussed.The arc device is operated at current of 50 A and argon flow rate of 0.35 slpm.It can be seen from figure 3 that in the case without protrusion,the temperature distribution of the arc column is axi-symmetric.However,in the case with the protrusion,the arc anode attachment shifts to the position of the protrusion.For the cases where the protrusion is located 1 mm and 2 mm away from the device axis, the protrusion makes the arc attachment more constricted,and a high temperature zone with a temperature of 10 000 K is formed in the arc column above the protrusion.In the case where the protrusion is located 3 mm away from the device axis, the constriction and attraction effects of the protrusion on the arc is weakened so that the maximum temperature around the protrusion decreases.The protrusions of the anode are intensively heated by arc plasma.The highest temperature at the tip of the protrusions in three cases has already exceeded the melting point of copper, 1357 K, which increases the likelihood of the protrusion being ablated.

Figure 4 presents the distributions of electron temperature and heavy-species temperature along they-direction 1.1 mm above the anode,i.e.0.1 mm above the protrusion.In the case without protrusion, the deviation of heavy-species temperature from electron temperature is small at the device axis, while the degree of thermodynamic non-equilibrium increases with the increase of distance from device axis.For the case with protrusion located aty=2 mm, the electron temperature around protrusion increases to 12 000 K due to the arc constriction, while the heavy-species temperature decreases to 5500 K.This indicates that the presence of anode protrusion strengthens the degree of thermodynamic nonequilibrium in this region.

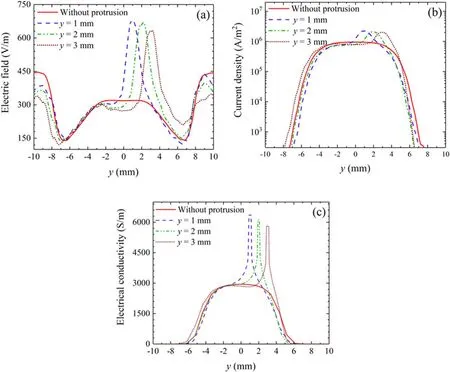
Figure 6.Distributions of (a) electric field strength, (b) current density and (c) electrical conductivity for the cases without and with protrusion at different radial positions of y=1 mm, y=2 mm, and y=3 mm.

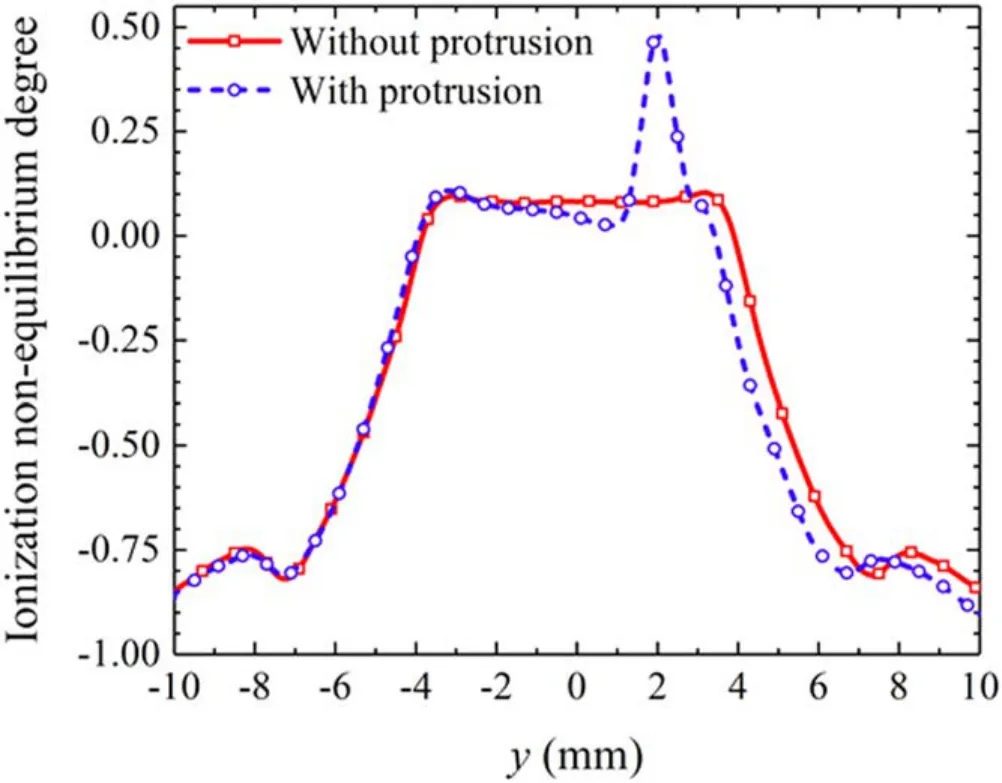
Figure 7.Ionization non-equilibrium degree distributions for the cases without and with protrusion at the radial position y=2 mm.

The comparisons of electron number density for different cases are shown in figure 5.The presence of protrusion leads to the electron number density near the protrusion being comparable to that in the central area of the outlet of the water-cooled constrictor tube.As the distance between the protrusion and the device axis decreases, the influence of the protrusion on the electron number density distribution around it increases.

3.3.Analysis of the effects of protrusion on the plasma nonequilibrium process near the anode

As presented above, the presence of protrusion causes the changes of parameters distribution,further leading to changes in the non-equilibrium plasma processes.Therefore, it is necessary to further analyze the influence of the presence of protrusion on the electric field strength, current density and electrical conductivity.The electric field, current density and electrical conductivity distributions along they-direction 1.1 mm above the anode, i.e.0.1 mm above the protrusion,are given in figure 6.It can be seen that the presence of protrusion greatly increases the electric field distribution.The current density and electrical conductivity also increase.Moreover, the closer the position of the protrusion is to the device axis, the more significant the increase in electric field strength, current density and electrical conductivity.

The chemical non-equilibrium process is essential to accurately and reasonably describe the characteristics of the plasma near the arc fringe and the electrode regions.The ionization non-equilibrium degree is calculated by the following equation [66]

Here,kiionandkirecrepresent the rate coefficient of ionization reaction and recombination reaction respectively.The ionization non-equilibrium degreeθis between −1 and 1.A value ofθequal to 1 indicates that only ionization reactions occur in plasma, whereas a value ofθequal to −1 indicates that only recombination reactions occur in plasma.Moreover, a value ofθequal to zero means that ionization-recombination equilibrium.

Figures 7 and 8 show the distributions of ionization nonequilibrium degree and ionization and recombination processes along they-direction 1.1 mm above the anode, i.e.0.1 mm above the protrusion respectively.In the case without protrusion,the degree is approximately 0.1 at the device axis,which indicates that the ionization and recombination reactions are close to equilibrium.However, the ionization non-equilibrium degree approaches −1 as the distance from device axis increases.This means that the ions and electrons are recombined to atoms in this region.

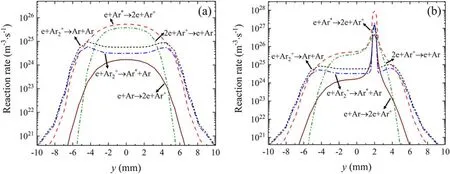
Figure 8.Ionization and recombination processes for the cases (a) without and (b) with protrusion at the radial position y=2 mm.

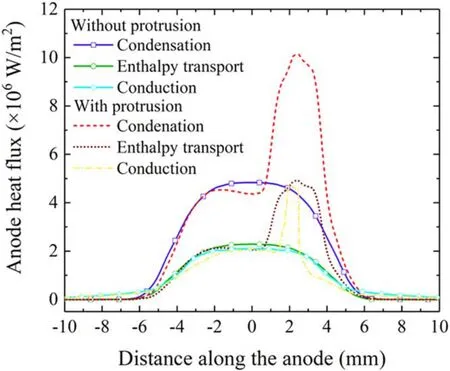
Figure 9.The main heating processes along the anode surface for the cases with and without protrusion at the radial position y=2 mm.

Figure 10.Experimental photo of a free burning argon arc with protrusion on anode.

It can be seen from the figure 8 that the main ionization and recombination mechanisms are respectively the ionization of the excited state of argon atom by electron impact and the three-body recombination of electrons and ions at the device axis.The chemical reaction rate of three-body recombination is slightly lower than that of argon atom excited state ionization.However, recombination reactions of molecular ions and electrons become the dominant reactions at the arc fringe.For the case with protrusion, ionization non-equilibrium degree increases to 0.5 at the protrusion, which is consistent with the increase of electron number density shown in figure 5.It can be seen that the increase of ionization nonequilibrium degree is caused by the considerable increase of rate of excited state atom ionization reaction.Moreover, the rates of recombination reactions have also increased.In addition to the three-body recombination reaction of electrons and atom ions,the recombination reactions of molecular ions and electrons also become important.

As shown in figures 3(b)–(d), the protrusion region on the anode surface is intensely heated by the plasma, making the tip temperature of protrusion much higher than other areas on the anode surface, which may further lead to anode material melting and ablation.Therefore,it is necessary to further analyze the main heating process that affects the temperature distribution of the protrusions.Figure 9 shows the distribution of heat flux on the anode surface with or without protrusion.In the attachment region, the electron condensation heat is dominant, and its value is higher than the electron enthalpy transport and heat conduction to the anode.For the case with protrusion,the peak heat flux density is almost twice that of the case without protrusion.The presence of protrusion penetrates into the high temperature plasma environment like pin ribs.The water cooling on the lower side of the anode is not enough to reduce the temperature of the top of protrusion,so that the heat at the top of the protrusion accumulates, and the temperature even exceeds the melting point of the metal material.

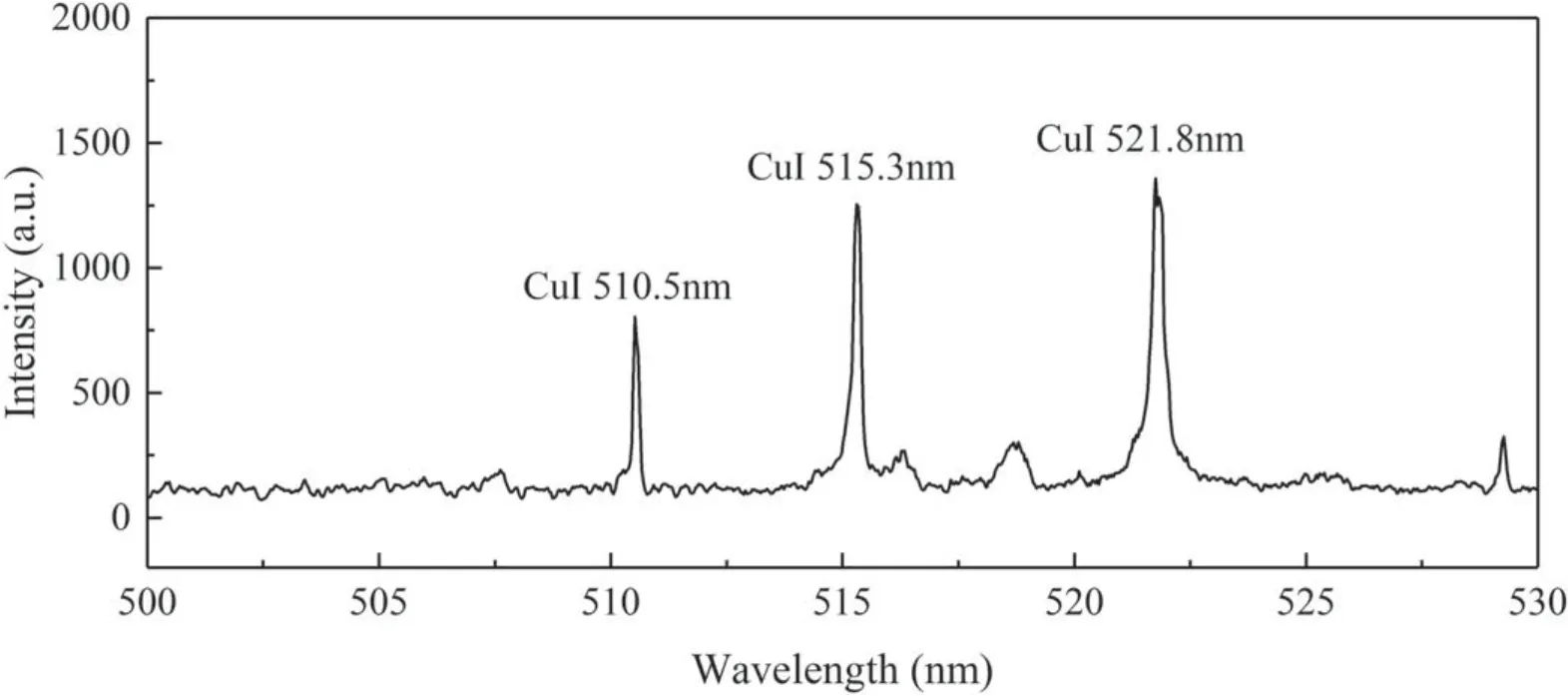
Figure 11.Spectral lines of copper vapor in free burning argon arc.

3.4.Preliminary experimental verification and discussion on the influence of protrusion on arc anode attachment

As mentioned above in this study, an artificially assumed millimeter-level protrusion on the anode surface is adopted to study the influence of the protrusion on the arc attachment.In order to verify the results of the numerical simulation,we also set up a protrusion of which the size is the same with that in numerical simulation, and conducted experimental observations on a free burning arc device as shown in figure 10.In the experiment, the free burning arc is operated at 50 A current and 15 mm electrodes gap.The presence of protrusion on the anode surface does cause the arc to deflect to the protrusion.It is worth noting that the high temperature of the surface of the protrusion extending into the arc leads to ablation, and the green metallic copper vapor can be observed in the arc fringe.The anode ablation and the presence of copper vapor can be verified by the spectral lines shown in figure 11.

Preliminary experiments verify the rationality of the numerical simulation in this paper, that is, the presence of protrusion on the anode surface will cause the arc deflection and the change of the arc attachment state.However,it should be pointed out that the current numerical simulation has certain limitations.The main problem is that the process of the metal evaporation in the protrusion area is not considered in a consistent manner.The ablation of protruding metallic copper will lead to two effects on the arc.First, it would change the chemical kinetic process,that is,the chemical nonequilibrium model used in the numerical simulation should take the chemical kinetic process related to copper into account, and second, it should further consider the impact of copper vapor on the plasma transport process and properties.Even with these shortcomings, considering the difficulty and complexity of the above-mentioned problems, our current work is still helpful to improve the understanding of the influence of protrusion on the arc anode attachment.

4.Conclusion

In this simulation, artificially assumed protrusion on the anode surface is used to study the influence of protrusion on arc attachment.Thermodynamic and chemical nonequilibrium models are used considering the importance of the non-equilibrium processes in the boundary layer and the arc fringe.Numerical simulation results show that the presence of protrusion causes the arc column deflect to the protrusion and increase of temperatures near the protrusion because of arc constriction.Compared to the case without protrusion,the presence of protrusion strengthens the degree of thermodynamic non-equilibrium around it.Moreover,protrusion extends into the high temperature plasma zone like the pin ribs, so that the protrusion is intensively heated, making the temperature much higher than other anode areas.Therefore, the anode ablation is more likely to occur at the protrusion.

The presence of protrusion significantly increases the electric field and current density around it.The closer the position of the protrusion is to the device axis,the more significant the increase in electric field strength and current density.The chemical reaction rates also change significantly near the protrusion.For the case with protrusion, the ionization non-equilibrium degree increases resulting in the production of electrons and ions around the protrusion.Moreover, both the electron–ion three-body recombination reaction and molecular ions recombination reactions become dominant recombination processes.

Preliminary experiments have qualitatively verified the rationality of the numerical simulation in this paper.In the experiment, the arc deflection caused by the presence of protrusion and the ablation caused by the high temperature in the protrusion tip were observed.Although the current nonequilibrium model used in numerical simulation has some limitations, it can still provide a reference for in-depth understanding of related processes.

Acknowledgments

This work was supported by National Natural Science Foundation of China (Nos.11735004 and 12005010).