在移动荷载作用下简支梁桥的结构损伤识别研究

陈 尧 罗雨舟

（1.西华大学土木建筑与环境学院， 四川 成都 610039；2.四川路桥桥梁工程有限公司， 四川 成都 610039）

0 引言

桥梁等基础设施随着其运行使用，设计功能会出现一定的损伤，这一不可避免的过程意味着很有必要对结构进行健康检测。由于各种不确定性和非均匀分布的环境影响，传统的损伤检测方法面临着很多挑战，并且传统的检测方法无法实现实时的桥梁损伤检测。

卷积神经网络，英语称为Convolutional Neural Network，简称CNN，思想源于Hubel等在1962年对动物视觉皮层细胞研究提出的感受野(Receptive Field)概念。近年来学界不断地提出新的CNN模型，与一些传统算法相融合是这些年CNN的发展趋势。因此CNN在众多领域获得了快速的应用扩展。通过CNN将结构加速度响应作为输入向量，李雪松等人系统对比经验模态分解法与小波包变化法，结果显示，CNN 自主提取的特征向量能更准确地反映结构的损伤情况[1]。Cha[2]等利用CNN自动的图像识别能力，在不结合图像识别技术的情况下，研究了CNN对混凝土结构裂缝等缺陷的图像识别精度。Duy-Tang Hoang[3]指出在振动信号中，含有很多能反映结构损伤的信息，将振动信号转化成二维灰度图像，利用CNN网络出色的图像识别能力，从中提取损伤特征并进行分类，以此来实现结构损伤识别因此，受到上述学者研究成果的启发，本文拟采用阶段式学习法与自主学习，研究CNN对结构损伤的个数和位置的判断，以及CNN对损伤横向分布的识别准确率。

1 卷积神经网络原理及结构

卷积神经网络的本质是原始输入数据经过多个卷积层和池化层的交替处理后，提取原始数据的特征信息，再映射到一个新的特征表达的数学模型。CNN是典型的前馈网络，先通过前馈运算从原始数据中提取数据特征，再利用反向传播算法进行网络参数的优化，求解出最优的权值与阈值。前馈运算，即是采用原始数据作为网络的输入，通过卷积层将原始数据中包含的各类特征进行提取和抽象，再由非线性激活函数激活后传入池化层，然后池化层把特征提取后的信息进行汇合和压缩，最后将数据通过全连接的方式继续向前运算得到计算值。所谓反向传播，即通过对比计算值与目标值之间的差距得到损失函数，依据BP反馈算法，将损失函数从最后一层向上一次逐层反馈，从而更新权值和阈值。因此，通过前馈运算与反馈运算，持续的更新网络的权值和阈值，直到损失函数逐渐收敛为止，这便是卷积神经网络的训练目的。

卷积神经网络组成部分一般有输入层、卷积层、池化层、全连接层和输出层，卷积层和池化层一般会取若干个，并交替设置，即一个卷积层连接一个池化层，池化层后再连接一个卷积层，依此类推[4]。卷积神经网络的核心就在于局部感受野，它是通过卷积层这一数学模型来模拟的。池化层也称为下采样层，是CNN网络的重要组成之一。池化层一般紧跟卷积层之后，其主要功能是汇总和压缩卷积层中提取到的特征，在一定程度上维持特征的尺度不变，提高泛化能力。在卷积深度网络结构中，在经过多个卷积层和多个池化层的交替传递后，连接着多个全连接层。全连接层的主要作用是整合卷积层和池化层中的局部信息。在全连接层中可采用例如Softmax函数进行分类。

2 确定CNN框架

本文进行了多次反复的试验，最终确定了第一阶段与第二阶段的CNN框架。对于第一阶段的CNN框架，本文设置了三个卷积层，三个池化层。经过认真的分析理解，在第一卷积层中，卷积核的数量设定为3个，尺寸大小为3×3。一般 CNN 中两层之间会含有多个卷积核，目的是学习出 Input 的不同特征，对应得到多个特征图。对于第二卷积层和第三卷积层，所以卷积核的数量设置为6个，尺寸同为3×3。池化层采用最大值池化，池化窗口为2×2。经过卷积与池化后，设置有两个全连接层。第一全连接层经过压缩后，有50个节点数量；第二全连接层压缩到10个节点数量。最后通过Softmax函数输出4个节点。在第二阶段，对于第一卷积层，设置了4个卷积核，第二、三卷积层，都设置了8个卷积核，且输出层设置了3个节点。两个阶段的具体CNN框架如图1～2所示。

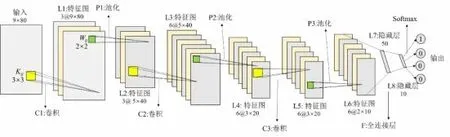
图1 第一阶段CNN框架

图2 第二阶段CNN框架

3 数值实验

3.1 装配式简支梁模型

为研究CNN对桥梁结构损伤的定位能力，本文利用有限元软件，构建了装配式简支梁模型，如图3所示。该简支梁模型一共设置了三个主梁，分别用数字编号为1～3。随机选取损伤一片主梁中4个连续的单元，并利用CNN识别损坏的主梁。该模型通过对梁单元刚度乘δ系数实现损伤方式，即δ·EI，δ为0.5～1上的随机数[5]。由三个横隔板将三片主梁连接，横隔板每单位长度的质量m取815kg/m，其他参数惯性矩I取0.022m4，横截面积A取0.3m2，弹性模量E取27.6GN/m2。在下图中，标记红点的位置，为加速度的采集位置。在本文有限元模拟中，自由荷载的大小，自由载荷的速度，损伤单元的单元号，损伤单元的损伤程度这四个量为随机量。因为要加快计算的速度，所以在每个样本中，采样点的采样个数都需要减少。经过减少后，每片主梁的信号都变成了3×80的矩阵，因此全模型为大小为9×80的输入矩阵。

图3 装配式简支梁模型

卷积神经网络的算法属于监督学习，对于CNN来说，就是将已知数据通过CNN训练后，然后再判断未知的数据。对于本文已建立的有限元模型，一共可以分成8种情况。在这8种情况里，有1种无损伤的情况，单片梁损伤的情况有3种。存在3种双片梁损伤的情况以及1种三片梁同时损伤的情况。理论上，这8种类型的数据可以使用一个数据集糅合起来，之后再对CNN模型进行训练。然而在训练过程中，作者发现CNN在训练集中的识别精度会迅速地回落至最低点在其上升小段之后。经过仔细认真的分析后，得到其主要原因为该CNN架构能够提取到的特征信息不够多。此外由于硬件的限制问题，很难有效的对更复杂的CNN框架进行训练。

为了克服上述的限制问题，本文采用了一种有效的方法，叫做阶段式学习法，该方法的具体步骤如图4所示。在第一阶段中，由首层CNN模型区分是几片梁损伤还是无损伤。第二阶段，初步分类的数据是特定CNN模型的输入，进而对损伤进行定位。该阶段的两个CNN模型，分别用数字1和2进行编号，两个模型进行训练时，使用不同的数据，因此互不影响。

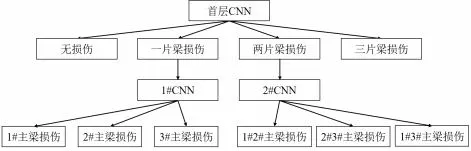
图4 阶段式学习流程

3.2 结果分析

在训练时，模型在优化的过程中，存在一定的随机性与不确定性，并且优化过程容易出现过拟合现象。在经过多次试验后，发现迭代步通常在8000～12000之间时，识别准确率开始逐步上升。在第一阶段试验过程中，CNN模型输入了4000个样本，其中每种类别各有1000个。经过多次反复地试验，发现对于无损伤情况、一片梁损伤以及两片梁损伤的情况，模型均能够较好的识别。其中无损伤情况的平均识别率达到了98.4%，一片梁损伤的情况的平均识别率达到了96.4%，对于两片梁同时损伤的情况，平均识别率达到了96.7%。对三片梁同时损伤的情况，模型出现了判断出错的情况，经过认真研究分析原因，是模型判断成损伤两片梁的情况。因此，本文对同时损伤三片梁的情况进行了单独训练，另外单独训练两片梁同时损失的情况作为对比。结果显示，相比之前的结果，三片梁同时损伤的识别精度有了明显的提高，平均识别率为89%，最高识别率达到了93%。

在第二阶段，本文以3000个样本（每种类别1000个样本）为CNN的训练集，对于CNN的预测集，同样用3000个样本，每种类别1000个，测试CNN的分类准确率。其结果显示，对于桥梁损伤，该CNN模型可以进行初步有效的定位。其中对于一片梁损伤的情况，平均识别准确率达到了96.7%；对于两片梁同时损伤的情况，平均识别准确率达到了97.8%。综合第一阶段与第二阶段的工作，CNN损伤定位的最终精度为第一阶段精度与第二阶段精度的乘积。因此最后汇总得出，CNN模型的分类精度如表1所示。

表1 CNN总准确率

4 结论

本文利用有限元软件，构建了一个装配式简支梁模型，同时搭建了相应的CNN框架，并且对于改模型，本文通过数值模拟数据进行了训练，从中提取结构损伤的特征信息，再将这些信息运用到实际结构的损伤识别诊断中。两个阶段的试验训练并测试了CNN对损伤横向分布的识别准确率，因为本文采用的阶段式学习法以及自主学习的优势，对于结构损伤的个数和位置，CNN识别判断的较为精确。

本文的结论大多为通过有限元数值分析所得到的理论值，缺乏实际数据对本文结论的佐证，因此对本文结论的实效性还需做进一步的深入研究。