求解具有非线性源项的双侧空间分数阶扩散方程的样条方法
陈雪娟,陈景华,2*,章红梅
(1.集美大学理学院,福建 厦门 361021 ;2.集美大学数字福建大数据建模与智能计算研究所,福建 厦门 361021;3.福州大学数学与计算机科学学院,福建 福州 350108)
近年来,研究者们在湍流、核磁共振、多孔介质中的渗透等系统中都观察到偏离布朗运动特性的扩散行为,而分数阶微分方程能够较精确地描述具有记忆和遗传、路径依赖性质的物理过程[1],因此分数阶微分方程目前已被用来描述诸多领域[2-4]中的反常扩散问题.从现实问题中抽象出分数阶微分方程之后,如何对分数阶微分方程进行求解成为一个迫切的研究课题.目前已有很多文献讨论了分数阶微分方程的解析解,但是这些解大多含有特殊函数(比如多变量的Mittag-Leffler函数[5-9]),要计算这些特殊函数相当困难,而且并非所有的分数阶微分方程都能得到其解析解,因此研究分数阶方程的数值模拟有着重要的理论与应用价值.国内外对分数阶微分方程数值解的研究也有一定的进展,主要采用的数值方法是有限差分[10-14]、有限元、谱方法[15-17]等;但是采用二次多项式样条函数进行数值逼近的研究文献却较缺乏.Sousa[18]研究线性分数阶扩散方程,借助样条函数近似离散分数阶导数,并在时间上采用Crank-Nicolson离散.Rashidinia等[19]提出一种新的非多项式样条方法数值求解二阶双曲线方程.Siraj等[20]构造了三次非多项式样条函数来求解非线性薛定谔方程.陈雪娟等[21]采用基于二次样条函数的数值方法求解分数阶扩散方程,但是处理的是单侧分数阶导数.较少文献涉及用样条方法数值求解双侧分数阶导数.由于双侧分数阶导数涉及到区间两个边界的函数值,比单侧分数阶导数能更好地模拟反常扩散现象,所以多用于定义空间变量的分数阶导数.
本文提出一种基于多项式样条函数的数值方法,用来求解具有非线性源的双侧空间分数阶扩散方程,同时证明了该数值方法是无条件稳定和收敛的.
考虑具有非线性源项的双侧空间分数阶扩散方程:
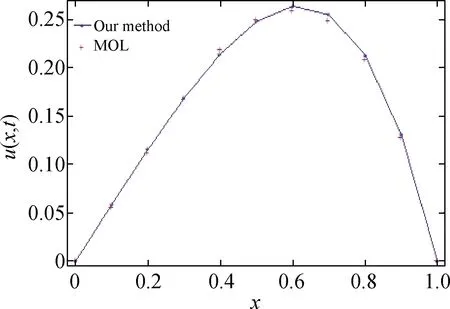
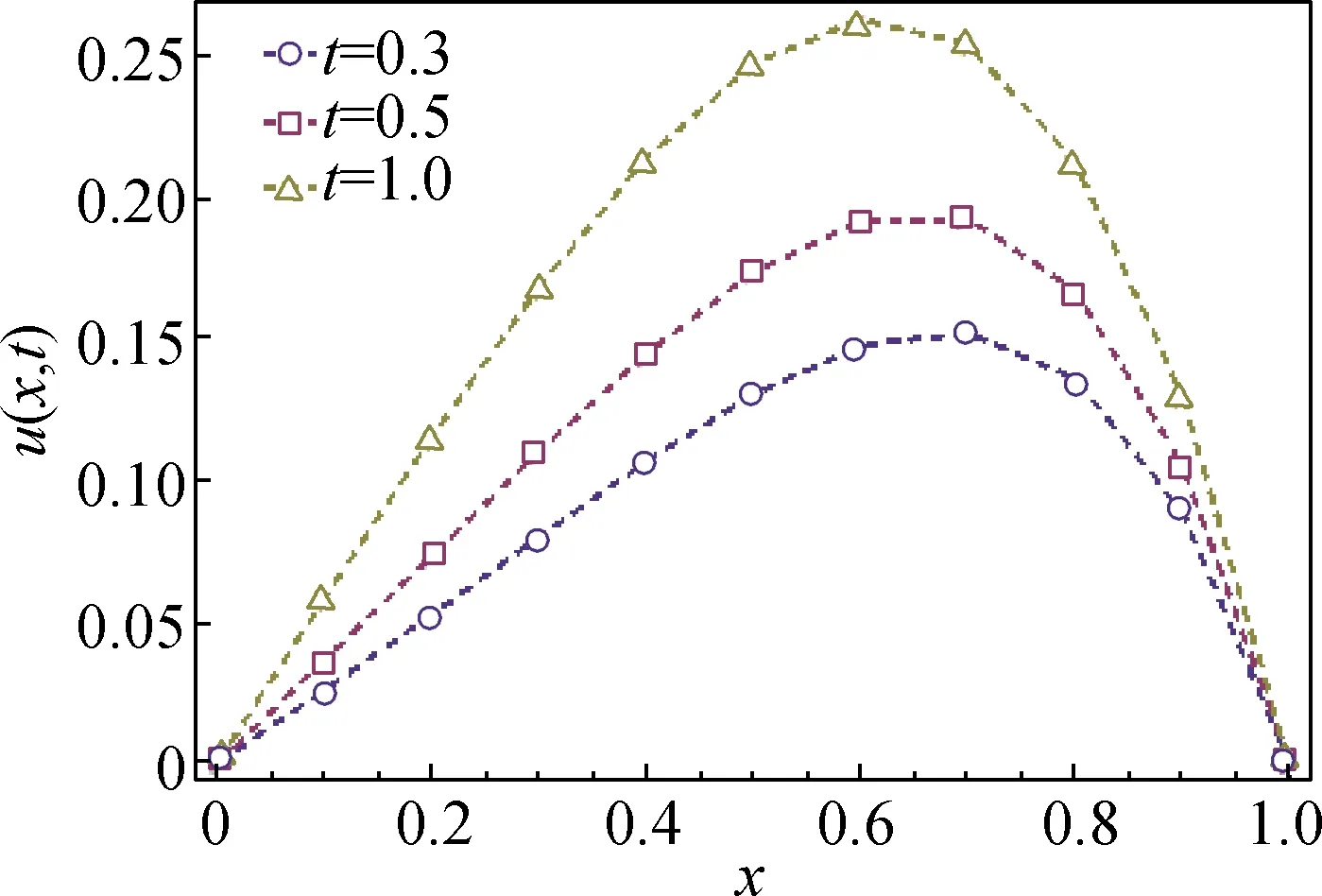
1<α≤2,a (1) 初始条件: u(x,0)=g(x),a (2) 具有Dirichlet零边界条件: u(a,t)=u(b,t)=0, 0≤t≤T. (3) 这里扩散系数λ1(x,t)>0和λ2(x,t)>0.非线性源项f(u,x,t)满足局部Lipschitz连续条件[22-23], 即存在某个常数L>0,使得 ‖f(u,x,t)-f(v,x,t)‖≤L‖u-v‖. (4) α阶的左、右侧Caputo导数分别定义如下[24]: (5) (6) 考虑如下二次多项式样条函数Pi(x,tj)(xi≤x Pi(x,tj)=ai(tj)(x-xi)2+bi(tj)(x-xi)+ ci(tj),i=0,1,2,…,m-1. (7) 为了确定函数Pi(x,tj)的系数表达式,定义: (8) (9) (10) 由方程(7)~(9)可以计算出: (11) 再由方程(7)和(10),及Caputo分数阶导数的定义可以推出: (12) 从而可以确定方程(7)的系数为: (13) 为了使二次函数pi(x,t)在x=xi,i=0,1,2,…,m-1处满足连续性条件 利用方程(13), 得到如下等式: (14) 进一步,可以计算出等式(14)的局部截断误差. O(h2). (15) (16) 这里, (17) 以下建立分数阶扩散方程(1)~(3)的差分格式. 由方程(1)可得: (18) 对时间导数采用向后差分格式,得到: o(τ), (19) 及 (20) 从方程(14)和(18)可得以下方程: (21) (22) (23) (24) 因此得到分数阶扩散方程(1)~(3)的数值逼近格式(22)~(24),且此数值格式的收敛阶为O(hα+τ). 本节讨论数值方法的收敛性和稳定性.将方程组(22)写成更简单的形式: (25) 为了证明数值方法的稳定性和收敛性,引入引理2. 引理2离散的Gronwall不等式[25].假设fk≥0,ζk≥0,k=0,1,2,…,并且ζk+1≤μζk+τfk,μ=1+C0τ,k=0,1,2,…,ζ0=0,这里C0≥0是常数, 则 由迭代格式(25), 得到误差方程: (26) 对j=1,2,…,n, 分别定义网格函数[26] 则εj(x)和ρj(x) 可分别展开成Fourier级数: 其中系数为 及 有 这里j=0,1,…,n. (27) 定理1数值离散格式(22)~(24)是无条件稳定的. 证明将式(27)代入迭代格式(26), 得到 则有 经过简单计算得到下列不等式: 因此有 |ξj|≤(|ξj-1|+τ|ηj-1|). (28) 则|ηj|≤L|ξj|.因此 |ξj|≤(1+τL)|ξj-1|,j=1,2,…,n. (29) 运用上式归纳得到 ‖εn‖2≤(1+Lτ)n‖ε0‖2≤eLT‖ε0‖2. 因此,证明了数值离散格式(25)是无条件稳定的. 根据迭代格式(25)的相容性,得到以下误差方程: (30) j=0,1,…,n. (31) 定理2数值离散格式(22)~(24)是无条件收敛的,并且存在正常数C>0使得: j=1,2,…,n. 证明将式(31)代入到迭代格式(30)中,得到: 经过简单的计算得到 2,…,n. (32) 这里C1是正常数. 从而 ‖ej‖2≤(1+τL)‖ej-1‖2+C1(hα+τ). 运用离散的Gronwall不等式(引理2)得到: C1TeLT(hα+τ)=C(hα+τ), (33) 这里C=C1TeLT. 因此,证明了数值离散格式(22)~(24)是无条件收敛的,且收敛为o(hα+τ). 一般分数阶微分方程的精确解是很难求得,因此为了说明数值方法的有效性,通常将所得的数值解结果与分数阶行方法(method of line,MOL)的解进行比较.分数阶MOL其本质是只离散空间变量,将分数阶偏微分方程转换成一组常微分方程加以求解.继而可以采用解决微分代数系统的工具DASSL来求解.2004年Liu等[27]首次运用分数阶MOL求解空间分数阶Fokker-Planck偏微分方程. 2u(xi-k+1,tj)+u(xi-k,tj)]}+ 2u(xk,tj)+u(xk-1,tj)]}+ u(xk-1,tj)]}+o(h2). 由此得到左、右侧Caputo分数阶导数的逼近格式: 2u(xi-k+1,tj)+u(xi-k,tj)]}, 2u(xk,tj)+u(xk-1,tj)]}. 因此,具有非线性源项的双侧空间分数扩散方程(1)~(3)的MOL可以写成以下形式: (34) 本节给出两个数值例子来证明所提出的理论分析的有效性. 例1考虑具有非线性源项的分数阶扩散方程: (35) 这里系数 λ1(x,t)=0.5Γ(5-α)x2+α(1-x)4et, λ2(x,t)=0.5Γ(5-α)x4(1-x)2+αet, 非线性源项为f(x,t,u)=u(x,t)+u2(x,t)·[-24x2+24x-12+2α(4-α)]. 图1是方程的精确解、数值格式(22)~(24)的数值解及MOL的数值解在t=1.0时刻的比较.取空间步长h=0.05,时间步长τ=0.01,α=1.5. 图1 t=1.0时刻,取α=1.5,h=0.05,τ=0.01,数值解与 分数阶MOL的解及精确解的比较Fig.1 Comparison of numerical solutions using our method, the MOL, and the exact solution at time t=1.0,α=1.5,h=0.05,τ=0.01 表1显示了在t=1.0时刻,α=1.5,不同的时间步长和空间步长(空间步长和时间步长的关系为h≈τ-α)下精确解与数值解的最大误差和误差率.可以看出 表1 在t=1.0时,取α=1.5,数值解与 精确解的最大误差及误差率Tab.1 The maximum errors and error rates for the numerical method relative to the exact solution at time t=1.0,α=1.5 说明数值解的收敛阶为o(hα+τ),这与本文中理论分析结果是相一致的. 从图1和表1中可以看出,基于二次多项式样条函数的数值方法与精确解很好地吻合. 例2考虑以下具有非线性源项的分数阶扩散方程: (36) 这里f(x,t,u)=u(1-u)+x2,此题精确解难以求得.因此考虑将数值解与分数阶MOL的数值解进行比较. 图2显示在t=1.0时刻, 取α=1.5,h=0.05,τ=0.01时数值解与分数阶MOL数值解的比较.图3显示了当α=1.5,h=0.05,τ=0.01时, 在不同时刻t=0.3,0.5,1.0的数值解的图形.图4显示了在t=1.0时刻取不同的分数阶导数值α=1.5,1.8,2.0时数值解的图形. 图2 t=1.0时刻,取α=1.5,h=0.05,τ=0.01,数值解与 分数阶MOL数值解的比较Fig.2 Comparison of numerical solutions using our method and the fractional MOL at time t=1.0,α=1.5,h=0.05,τ=0.01 图3 取α=1.5,h=0.05,τ=0.01,本文方法 在不同时刻的数值解比较Fig.3 Comparison of numerical solutions using our method at different times when α=1.5,h=0.05,τ=0.01 本文提出了一种基于多项式样条函数的数值离散格式,用于求解具有非线性源项的双侧空间分数阶扩散方程,其中的分数阶导数采用Caputo分数阶导数;同时,提出一种计算分数阶微分方程数值解的计算技巧,即分数阶MOL.证明了提出的数值离散格式是无条件稳定和收敛的,且收敛阶为o(hα+τ)(1<α≤2).最后,给出数值例子证明了方法的有效性.这种样条方法和分析技术可用于求解和分析其他类型的分数阶偏微分方程.1 样条配置法

1.1 二次多项式样条函数

1.2 构造数值方法

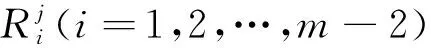
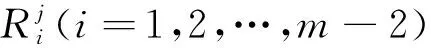



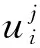


2 数值方法的稳定性和收敛性分析
2.1 稳定性分析
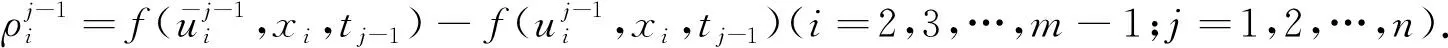





2.2 收敛性分析
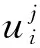

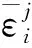


3 分数阶行方法


4 数值例子


5 结 论

