基于模糊集的陶质文物碎片点云特征提取算法
王淑睿,郭 宝,郭锐哲,耿国华,周芯羽,张雨禾
(1.西北大学 文化遗产数字化国家地方联合工程研究中心,陕西 西安 710127;2.西北大学 信息科学与技术学院,陕西 西安 710127)
近年来,点云模型处理广泛地与医学[1-2]、艺术[3]以及文物数字化保护与复原[4]等领域相结合,这得益于三维扫描技术的快速发展,极大地加快了点云模型处理技术的研究进度。作为最基本的曲面几何形状的特征基元,特征点对于几何模型的外观及其准确表达起着十分重要的作用[1]。特征提取为数字几何领域的许多研究提供了重要途径,如几何分析、曲面配准、曲面重建以及基于几何特征的点云去噪和简化等,成为备受关注的底层技术之一。
在实际应用场景中,采集到的点云模型往往存在噪声影响和数据缺失等问题,且模型中各点之间并不具有显著的拓扑关系,这使得点云模型的特征提取难度远大于网格模型。本文将点云模型特征提取技术大致分为以下几种:①基于协方差分析和最小生成树,文献[5-6]对于提取点云上特征线的基本思路,均为先构造特征点集的最小生成树,再优化该最小生成树。具体来说,Gumhold等首先构造黎曼树表示点数据上的邻域信息,然后利用协方差分析方法为每个点计算一个权重,该权重被用作判断其为棱点、边点以及角点的标记[5]。Pauly等在特征点的提取中,以局部邻域大小作为离散的尺度参数,计算一点在不同尺度下成为特征点的可能性,通过引入多尺度的理论来对含有噪声的模型进行处理[6]。基于多尺度理论的特征提取方法还有文献[7],通过综合考虑不同尺度下的数据特征,可以增加特征检测方法的鲁棒性和抗噪能力[7]。②基于法向估计和聚类思想,Demarsin等首先用PCA方法对点云模型各点的法向量进行计算,在此基础上,以法向量的变化为依据,采用区域生长策略进行点数据的划分,以得到数据的初始聚类,最后通过分割不同聚类的边缘点云数据构造出最小生成树,从而得到封闭特征线[8]。Weber等提出的特征提取方法基于高斯法向聚类的思想,采用高斯法向聚类方法对一点局部邻域内由该点组成的所有可能的三角形的法向进行聚类,判定该点是否为特征点的依据是法向聚类的个数[9]。You等介绍了一种基于示例的子空间聚类方法,以解决几何拟合任务中的数据不平衡问题[10]。通过测量表示系数的L1范数,他们搜索最能代表所有数据点的数据子集。王小超等考虑了基于局部重建的方法,对潜在特征点构建的不跨越特征区域的三角形的法向进行聚类,这样可以得到对应局部区域的数据点分类集合,然后对每一类点拟合平面,根据该点是否同时落在多个平面上作为特征提取的关键条件[11]。③基于投影映射的方法,庞旭芳等首先用点云模型中绝对值较大的主曲率标记潜在谷脊特征点集合,然后平滑潜在特征点来得到平滑的谷脊线,具体做法是将得到的特征点投影到其邻域点构成的主轴上[12]。Daniels等以当前点在基于最小平方中值和前向搜索法的RMLS方法得到的拟合曲面上的投影残差值的大小,来确定是否标记其为潜在特征点[13]。Kang等建立了一个由两个同心圆组成的自适应半径的圆形模型,将非接地点按照选定的间隔划分为若干个切片,通过基于体素的形状识别生成一组线性体素,并对生成的线性体素及其相邻的线性体素进行聚类,然后将聚集点投影到关联的切片平面[14]。Xu等采用截面投影法来提取和分析点云,对环形数据进行投影和迭代滤波,将点云数据分割成薄片,并获取每个截面轮廓中的投影平面,以提高精度[15]。Wushour等首先估算了散乱点云法向量,并用张量投票法对其进行平滑估算,最后,计算采样点以及其对应的加权邻域重心之间的距离,并将该距离向法向方向进行投影,这种方法可以有效地消除因为采样密度不均匀以及边界点所引起的尖锐特征点误判问题[16]。④其他方法,Chica基于视觉投票的方法提取点云模型的特征[17],Mérigot等的方法采用了Voronoi协方差度量[18],在进行特征点检测时,王丽辉等为每个数据点定义了一个基于曲率和密度的特征参数[19]。Huang等提出通过提取多尺度特征表示,并将其局部嵌入到低维鲁棒子空间中,在该子空间中获得更紧凑的表示,同时保留数据的固有结构,从而减少硬阈值选择策略带来的信息丢失[20]。
1 研究方法
针对采自分片光滑曲面的陶质文物碎片散乱点云模型P={pi},pi∈R3,i∈{1,…,N},其中,P为构成整个点云模型的点的集合,R为点云模型外包圆的半径,本文提出一种特征提取算法,首先,基于法向估计和区域生长的思想,以特征点位于多个潜在分片光滑曲面相交区域为依据,提出一种基于模糊集的区域生长法,利用点的隶属度作为判据,将每个潜在曲面生成一个区域,不同区域相交部分的点被标记为潜在特征点。然后,采用权重敏感的移动最小二乘法对点的邻域拟合局部平面,基于多尺度理论,在计算点的局部拟合平面时,以局部邻域大小作为离散的尺度。接下来将点在不同局部平面的投影残差作为特征值,当点的投影残差在两个连续的度量中都大于给定阈值时,则认为该点是特征点。最后,采用“双生长圆”策略,生成特征折线,并对其进行平滑扰动处理,最终得到平滑的特征线。算法通过以下3个步骤来完成,如图1所示。

图1 本文特征提取方法流程图Fig.1 Flow chart of proposed feature extraction method
1.1 邻域选择
特征点可以被描述为在局部范围内法向变化较大的点,即与其邻域点法向间夹角较大的点。采样密度均匀的点云模型的点邻域选取较为简单,通常取一个点的k个最近邻点来代表其邻域。但在实际应用中,点云模型的采样密度往往是不均匀的,这就导致模型特征点的k个最近邻点可能是位于其一侧而非多侧区域内,如图2所示。为了解决这一问题,本文采用Delaunay邻域[21],如图3A所示,针对点云模型上的任一点p,首先,建立满足式(1)的球邻域Nball,
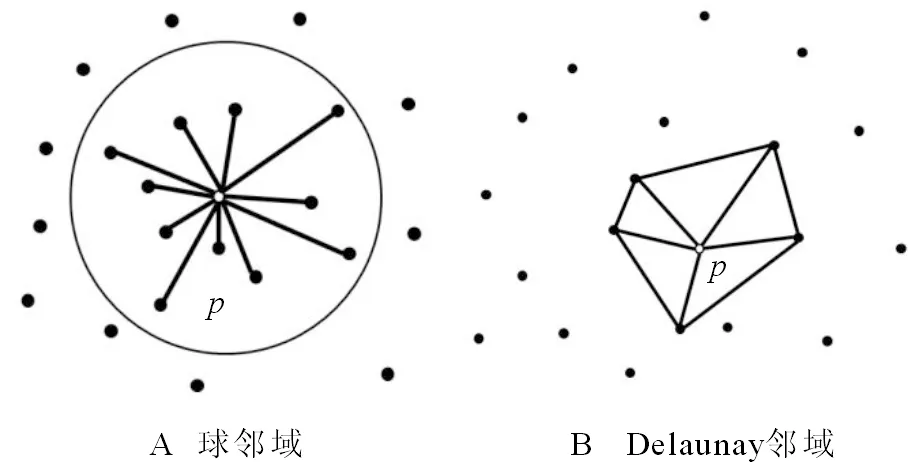
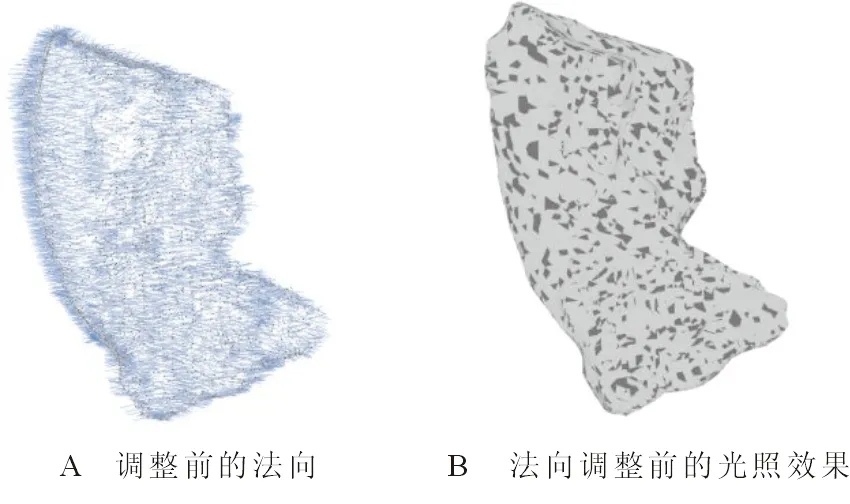
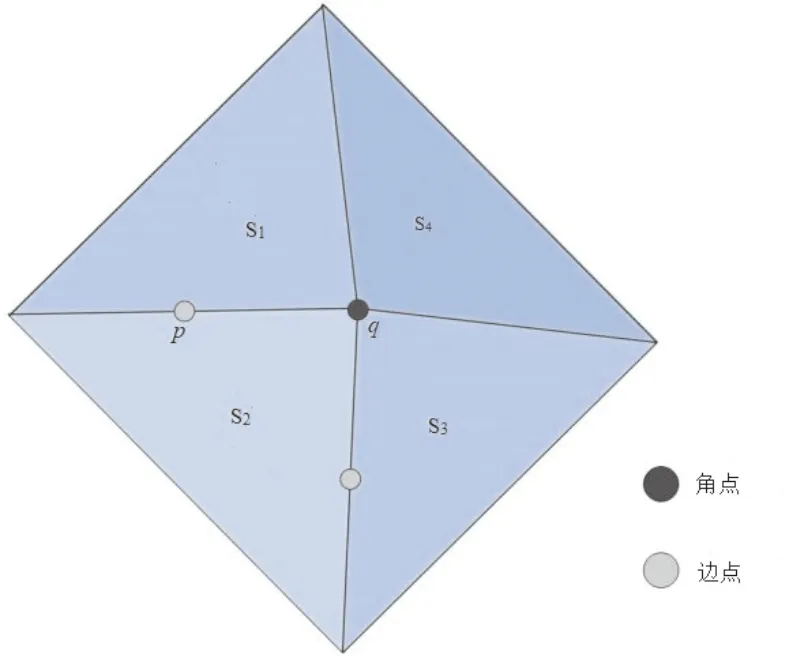
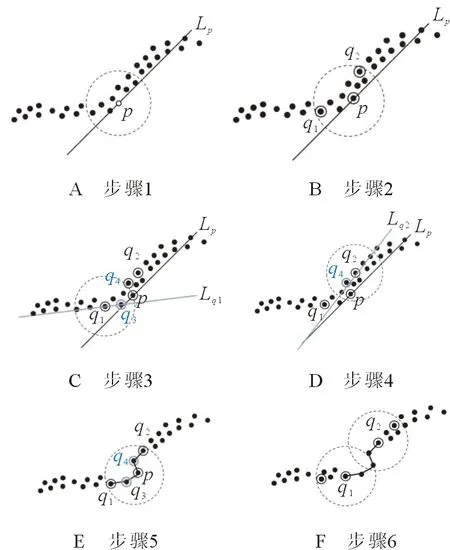
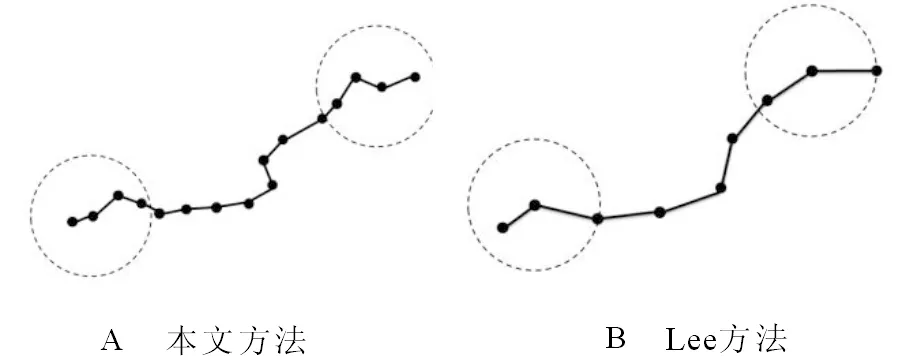
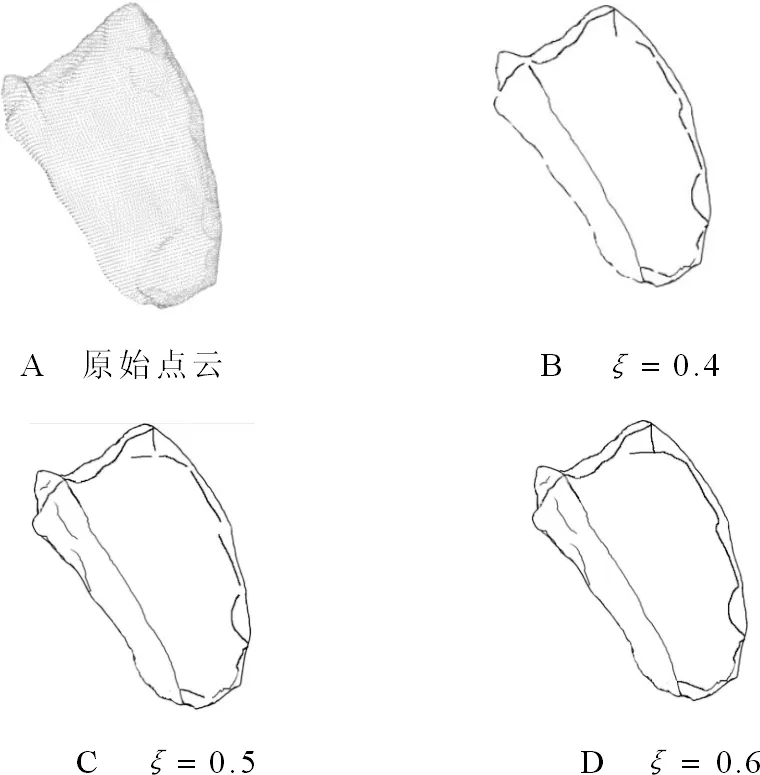
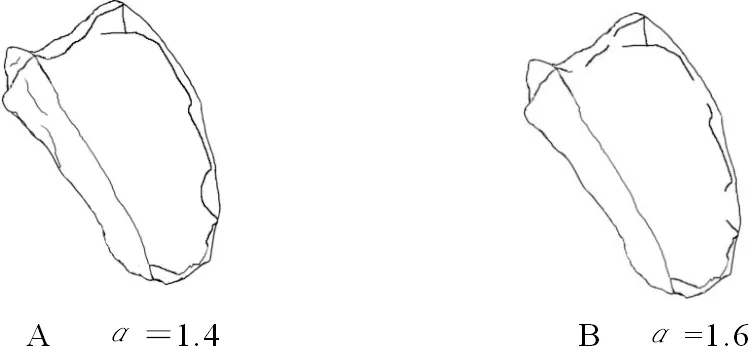
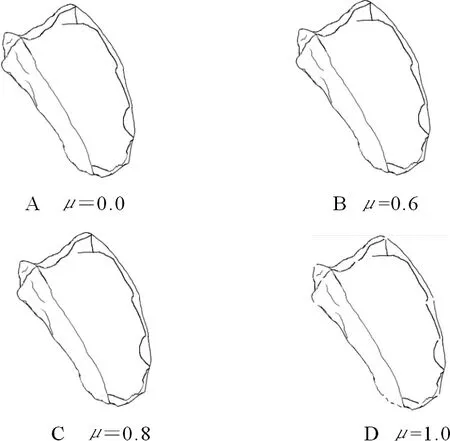
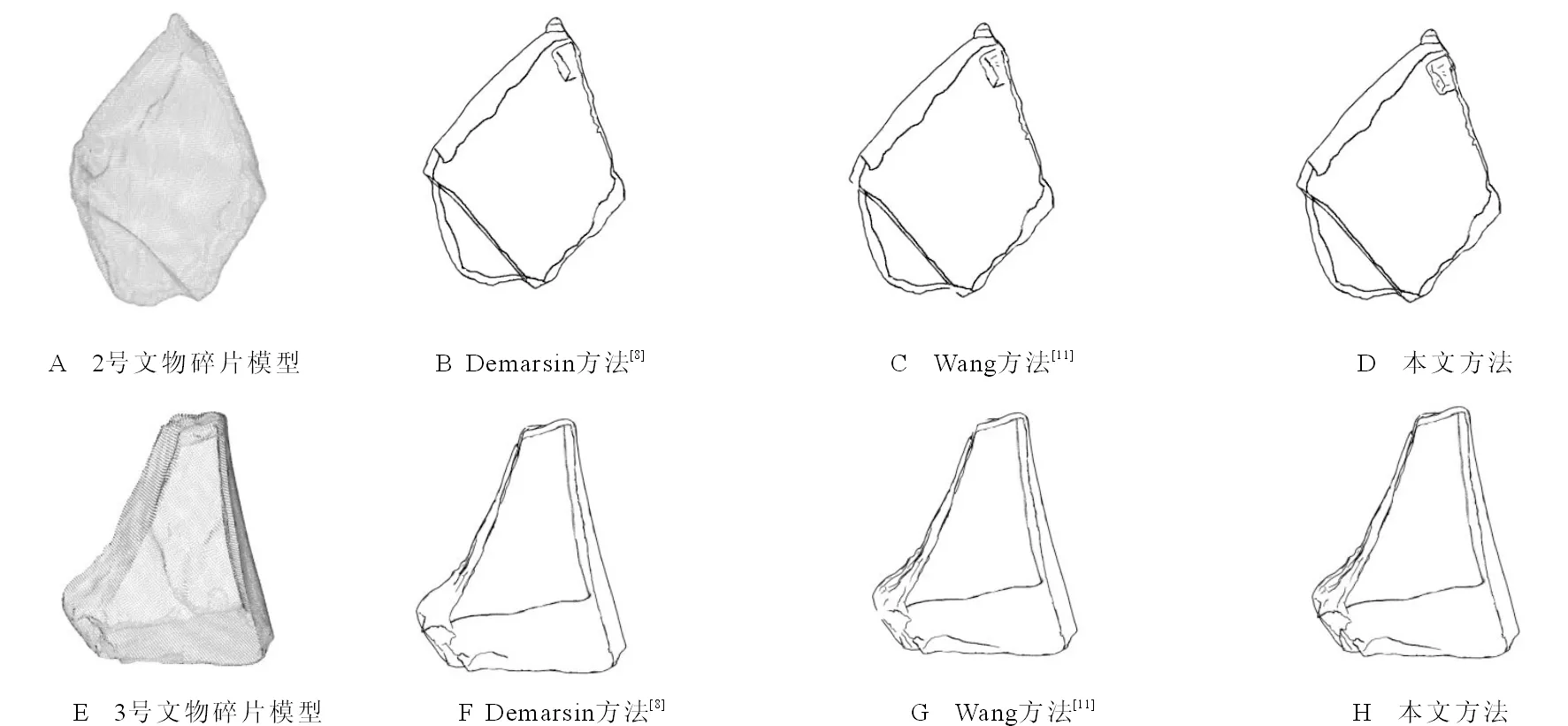
Nball={j:0<‖pj-p‖ (1) 其中,r为球邻域的半径。如图3B所示,为了使点p的邻域点可以尽可能均匀地分布于点p周围,球邻域内需要包含尽量多的近邻点,因此,其半径的选取应足够大。然后,对球邻域内的点pj拟合局部平面,将点p及其邻域点pj沿拟和平面法向方向拟合平面做投影,点到投影点q和qj。最后,利用Delaunay三角剖分方法对投影点qj进行处理,根据式(2)得到点p的Delaunay邻域Np, Np={pj:qj与q共享边}。 (2) 图2 点p的k近邻Fig.2 k-nearest neighbors of point p 图3 球邻域和Delaunay邻域Fig.3 Spherical neighborhood and Delaunay neighborhood 法向夹角的变化可以作为衡量曲面上光滑和突变区域的度量。本文通过计算点云模型中点的法向与其邻域点法向的夹角作为隶属度函数的参数,计算一点的隶属度,进而标定潜在特征点。因此,首先需要计算点云上点的法向,本文采用协方差分析法,对点云中每个点p及其邻域点pj∈Np进行协方差分析,协方差矩阵T如式(3)所示,对应于T最小特征值的特征向量v0被当作点p的法向量。 (3) 其中, (4) o是Np的质心。需要注意的是,利用上述方法得到的点法向有的指向三维模型内部,有的指向外部,如图4所示。本文需计算顶点与近邻点的法向夹角,因此,需要为法向建立一个统一的参照,使法向指向三维模型的外部,调整法向后的结果如图5所示。 图4 法向调整前的效果Fig.4 Effect before normal adjustment 图5 法向量调整后的效果Fig.5 Effect after normal adjustment 在几何造型领域,特征点一般被定义为法向在局部邻域内不能保持一阶连续的点。例如,棱点和角点均为典型的特征点,与一般情况下仅落在某一曲面内的非特征点不同,特征点往往落在多个潜在分片光滑曲面的相交区域[11]。因此,特征点会同时属于多个曲面,但隶属度可能不同。如图6所示,点p为棱点,同时属于S1和S2区域,但在两个区域的隶属度可能不同。点q为角点,同时属于S1、S2、S3、S4这4个区域,同理,在4个区域的隶属度也不同。Ge等利用种子点和相邻点之间的法线差异进行相似性度量[22],其中,点的法线由拟合到该点及其4个连接点的平面的法线表示,Wang等通过考虑全局视图而非局部视图来进行区域生长的初始种子点选取和控制区域生长的标准[23],结合以上分析,基于文献[8]和文献[22-23],提出一种基于模糊集的区域生长法,将每个潜在曲面生长为一个区域,区域间相交部分的点被标记为潜在特征点。 对于潜在特征点的标定,基于如下原则,将区域中非特征点的隶属度赋值为1,点越靠近平滑区域,法向在局部范围内变化越小,隶属度越大。相反,点越靠近边界,法向在局部范围内变化越大,隶属度越小。当点在某区域的隶属度大于0时,则认为该点隶属于当前区域。最终将隶属于种子点所在区域,即隶属度大于0的点集合起来构成区域。 图6 特征点位置Fig.6 Position of feature points 与传统区域生长法的不同在于:①基于模糊集的区域生长法,将隶属度作为判定条件,判定一点是否属于当前区域。从一定程度上避免了传统方法中采用硬阈值作为判定条件造成过划分或错误划分的问题。②种子点的选取范围为那些隶属度大于给定阈值的点,避免在区域生长的过程中,将边界点作为种子点,将另一个区域也包括进来。③在区域生长的过程中,由于特征点往往在潜在曲面的边界区域,因此点的搜索范围包括未被划分的点,以及那些已被划分到其他区域且隶属度均不等于1的点。从而,基于模糊集的区域生长法划分的不同区域间会有相交,相交部分的点将被标定为潜在特征点,具体步骤为: 1)在待分割的区域,选择一个非特征点p作为种子点,该点的隶属度赋值为1。在判定一点p是否为非特征点时,利用点p与其邻域点pj∈Np间的法向夹角和作为特征值, (5) 其中,θpj为点p与其邻域点pj的法向夹角。设定一个合适的阈值τ,将潜在特征点与非特征点进行区分,当fp<τ时,点p为非特征点,此时可被选作区域生长起点,否则不能。为了避免将特征点隶属度误赋为1而造成特征点漏判的问题,在τ的设定中应尽量选择较为严格的阈值。本文计算了模型平均点法向夹角的均值,目的是使得算法能够自适应地根据模型来确定合适的阈值。同时,考虑到算法的计算成本,仅计算模型中任意m(m>N/20)个点与其邻近点的法向夹角均值μA。本文实验中,取τ=0.7·k·μA,可以得到满意的结果。 2)根据隶属度函数,计算点p邻域点pj∈Np的隶属度,将隶属度大于0的点合并到生长起点所在的区域中。本文设定的隶属度函数为 (6) 当点pj与点p的夹角∠A大于某一特定阈值h1时,点pj在当前区域的隶属度为0,即点pj不属于当前区域;当点pj与点p的夹角∠A小于某一特定阈值h2时,点pj在当前区域的隶属度为1,点pj属于当前区域且为非特征点;当点pj与点p的夹角∠A处于h1和h2之间时,点pj在当前区域的隶属度根据式(6)计算,并且满足0 h1和h2的设定,应选择较严格的阈值。h1界定了同一区域中两个相邻点法向夹角的最大值,保证区域划分的有效性,避免一个区域的生长过程中越过边界将另一个区域包括进来。h2直接断定了点是否为特征点,如果h2设置得较大,部分潜在特征点会被误判成非特征点而造成特征点漏判的问题。本文实验中取h1为均值μA的2~4倍,h2为0.7·μA时,能够得到满意的结果。 3)隶属度大于0的点被包括到当前区域,这些新加入的点中,隶属度大于给定阈值η的点,才能被当作新的种子点,然后继续步骤(2),直到没有隶属度大于给定阈值的点可被包括进来,这样就完成了一个区域的生长。η判定了一个点能否作为新的种子点继续区域生长,因此,η的设定应选择较严格的阈值,尽量使η接近边界点的隶属度,避免当前区域生长不完整,同时还要避免跨越边界将另一个区域完全包括进来。本文实验中,取η为0.2~0.3时,可以获得较好的结果。 当所有点都被划分到不同区域中后,即找不到新的区域生长起点时,算法结束。不同区域间相交部分,即具有多个隶属度且隶属度均满足0 潜在特征点集B和C中包含了很多伪特征点,需要对其中的点进行判定,筛掉伪特征点,保留特征点。为进一步识别特征点,将B和C中的点向局部平面P做投影,计算该点为特征点的可能性γp。同时,为了提高特征检测的鲁棒性和抗噪能力,方法在进行特征提取过程中计算并综合考虑了点在不同尺度下成为特征点的可能性。 由于潜在曲面边界上的点往往距离局部拟合平面较远,因此点在局部拟合平面上的投影残差会较大[13]。据此,在进行特征点的判定时,本文将点到局部拟合平面的投影残差作为特征值对其进行度量。首先,通过对给定点p∈B(或p∈C)进行局部邻域的协方差分析(协方差矩阵T如式(3)所示),得到λi为T的特征值且λ0≤λ1≤λ2,分别对应特征向量v0、v1、v2,其中v0为主轴矢量。然后采用权重敏感的移动最小二乘法,进行局部平面P的拟合,该方法的拟合结果不局限于点的坐标影响,而是将点的权重影响纳入拟合结果,即拟合满足式(7)的平面P,这一点是与一般应用中坐标敏感的最小二乘法不同, (7) 其中,d为p到坐标原点的距离;n为平面p的法向量,式中的权函数为 (8) 其中,dv1j(o)为邻域点pj沿主轴矢量v0距离质心o的距离,距离质心o越远,权重越小。最后,将点p及其邻域点pj∈Np沿平面P法向n方向向平面P做投影,得到投影点q和qj,式(9)计算邻域点投影残差值, rpj=‖pj-qj‖。 (9) 利用式(10)进行判定, (10) 其中,μrpj和σrpj分别为点p邻域点在平面P上投影残差的均值和标准差,如式(11)、(12)所示, (11) (12) 通过设定阈值α过滤伪特征点,基于多尺度,在计算点在局部拟合平面时,点的邻域分别选择k-1阶、k阶、k+1阶的Delaunay邻域,如图7所示分别为一阶和二阶Delaunay邻域,当点在两个连续的度量(k-1阶、k阶或k阶、k+1阶)中,都满足γp>α时,则认为该点为特征点,否则,该点则为伪特征点,从B(或C)中删除,最终得到棱点集B*和角点集C*。 为了简化角点的表示,将在一定半径ε内的角点用一个角点表示[13]。取点p∈C*半径为ε的球邻域Nballp中距离质心最近的点作为代表,同时,将Nballp内的其他点转移到B*中。 图7 不同大小的Delaunay邻域Fig.7 Delaunay neighborhood of different sizes 为了提取特征线,需在特征点集B*中选取合适的点并建立连接关系。借鉴文献[24]中的方法,采用“双生长圆”折线生长算法,半径r控制特征折线的生成精度,由用户输入。具体步骤为: 1)将B*中的点按照其离最近角点的距离依次加入优先队列,且距离越大的棱点优先度越高,每次从优先队列中取出一个棱点p,作为特征折线生长的“初始生长点”。选定初始生长点后,以初始生长点为圆心,半径为r的圆即为上文提到的“生长圆”。 2)如图8A所示,首先对初始生长点生长圆内邻点NRp进行主元分析,主轴矢量确定为NRp协方差矩阵的最大特征值对应的特征向量。接下来,将NRp内的每个点都投影到由主轴矢量和点p确定的直线Lp上。此时,由投影位置来确定新的生长点,取投影最远的两个远端点q1、q2作为新生长点,如图8B所示。 3)为了得到更为平滑的特征折线,分别对q1、q2及其生长圆内的邻点NRq1、NRq2进行主成分分析得到主方向矢量,与步骤2)类似,将NRq1(NRq2)内的点投影到由主轴矢量和点q1(q2)确定的直线Lq1(Lq2)上,取投影较远且尽量满足‖pq3‖≈‖q1q3‖(‖pq4‖≈‖q2q4‖)的点q3(q4),如图8C、D所示。依次连接p、q3、q1(p、q4、q2),同时,将NRp内的点从优先队列中删除,如图8E所示。 4)从新的“生长点”(点q1,q2)开始继续生成折线并检测下一个“生长点”,如图8F所示。当检测不到新的生长点时,该条特征折线“生长”完成。重新从优先队列中选取“初始生长点”,重复步骤2)~3),直到优先队列为空。 图8 特征折线的生长 Fig.8 Growth of characteristic polylines 如图9A所示为本文方法折线生长结果,图9B为文献[24]方法所生成的折线,从图中可以看出,本文方法生成的特征折线能够保留更多细节且更为平滑。 图9 特征折线生长对比Fig.9 Comparison of the growth of characteristic polylines 在潜在特征点的标定中,具有多个隶属度且隶属度均满足0 图10 ξ取不同值的特征提取结果Fig.10 Feature extraction results when ξ takes different values 在特征提取方法中,γp>α的点被认定为是特征点,而γp<α的点则被认定为是非特征点。α的取值界定了提取出的特征点的尖锐程度,α取较大值,较平滑的特征将会被过滤掉,只保留了较尖锐的特征;α取值较小,则能够保留更多的特征,但同时也可能会造成特征提取错误的问题。图11为α=1.4和α=1.6时,1号文物碎片模型(原始点云模型如图10A所示)的特征提取效果。 由于本文方法在特征提取时多尺度理论,因此本文方法具有一定的鲁棒性。图12为1号文物碎片模型在不同噪声尺度下的特征提取结果,添加噪声的方法参考文献[12],μ表示加入噪声的程度。从图中可以看出,本文方法在具有适度噪声的情况下,仍然可以很好地提取出特征线,具有一定的鲁棒性,但随着噪声的增大,受噪声的干扰,有些特征点会被遗漏。 图11 α取不同值的特征提取结果Fig.11 Feature extraction results when α takes different values 图12 不同噪声影响下的特征提取结果Fig.12 Feature extraction results under the influence of different noises 图13为分别使用文献[8]、文献[11]和本文方法进行特征提取的结果对比。模型均为陶制文物碎片点云模型,包含尖锐特征以及相对较平滑的特征,既存在采样较好的区域,也存在采样不均的区域。由于破碎陶制文物碎片具有一定的缺损,模型中均存在由4~7个曲面交合而成的角点,如图13A和13E所示。图13B和图13F为文献[8]的方法,同样基于区域生长法,文献[8]可以很好地提取出模型的尖锐特征,但较平滑的特征则被遗漏。其主要原因在于传统的区域生长法采用了硬阈值,当阈值较严格时,会过滤掉较平滑的特征,当阈值较宽松时,会造成将非特征点误判成特征点而造成特征提取错误的问题。图13C和图13G为文献[11]的方法,采用基于局部重建的策略,文献[11]可以有效地提取出尖锐特征、部分较平滑特征以及部分角点。但是当角点由5~6个曲面交合而成时,文献[11]的方法有效性较低,不能很好地提取出该类型的角点。图13D和图13H为本文方法特征提取结果,由于采用了基于模糊集的区域生长法,利用隶属度标定潜在特征点,并且在特征提取方法中,依靠点的局部特征信息进行判别,这样的方法免去了对角点邻域的局部拟合平面数这一难点的考虑,从而可以有效地提取出多个曲面交合所形成的角点。该方法从一定程度上解决了传统区域生长法中的过划分或错误划分的问题,通过设定合适的阈值,不仅能够有效地提取出尖锐特征,还可以尽可能地保留较平滑的特征。 图13 实验结果对比Fig.13 Comparison of experimental results 本文提出了一种具有鲁棒性的特征提取方法,在一定程度上解决了传统区域生长法中采用硬阈值造成的错误划分或过划分问题。以特征点位于多个潜在分片光滑曲面相交区域为依据,针对采自分片光滑曲面的散乱点云,利用基于模糊集的区域生长法标定潜在特征点;同时,在处理角点时,不受限于交合形成角点的曲面个数,有效地提取各类角点信息。在提取特征点时,将点在局部拟合平面上的投影残差作为特征度量,方法上引入了多尺度理论,这样能够大大提高特征检测的鲁棒性和抗噪能力。最后,采用“双生长圆”策略生成特征折线,能够保留更多细节且生成的特征折线更为平滑。本文方法在有效、准确地识别出尖锐特征的同时,还能保留相对较平滑的特征,针对含有孔洞、曲面较多以及特征线结构较复杂的模型,仍能得到较好的效果。 尽管本文方法可以有效、准确地提取点云模型的特征,但是所设定的参数不能根据模型中的各部分进行调整,因此会影响算法的结果。将来的研究工作是采用智能方法根据模型各部分动态调整阈值。同时,基于模糊集的区域生长法的计算量较大,寻求一种更高效的预处理算法将是一个有意义的研究方向。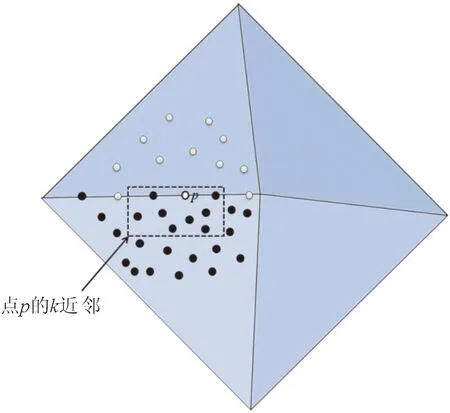
1.2 法向估计

1.3 潜在特征点标定
1.4 特征提取

1.5 特征折线的生成及优化处理
2 实验结果与分析
2.1 参数说明
2.2 实验结果
3 结语

