基于LSTM神经网络的时间序列证券价格趋势预测

摘 要：针对国家对证券市场的监管和投资人对证券市场的决策而言，一个精确度更高的时间序列预测模型是很重要的。本文在吸取前人利用神经网络模型进行证券价格趋势预测中的经验，基于长短期记忆人工神经网络搭建时间序列，提出利用指数移动平均值均线对数据进行采样，以提高时间序列对证券价格趋势预测的准确性。本文采用的时间序列数据为上证指数日线收盘价，实验结果表明预测精确度提高70%，采用指数移动平均值均线对数据进行采样输入时间序列分析模型的预测效果优于传统方法进行数据采样。本文的实验结果为国家对市场的监督和投资者的决策提供了一定参考。

关键词：时间序列;指数移动平均值;神经网络;LSTM;深度学习

本文索引：陈腾劲 .<变量 2>[J].中国商论，2021（20）：-094.

中图分类号：F832.0 文献标识码：A 文章编号：2096-0298（2021）10（b）--03

时间序列分析是以已有的历史数据为根据，通过数学建模进行分析和判断未来发展趋势的一种手段，被广泛地运用在证券走势的预测当中。自20世纪80年代开始，在人工智能（Artificial Intelligence， AI）領域，人工神经网络（Artificial Neural Networks， ANN）受到越来越多的关注。得益于最近十多年来科技的进步，人们在半导体领域的探索不断深入，ANN的研究工作也不断向前迈进，已经取得了很大的进展。传统的时间序列分析方法因其对高噪声序列分析的效果不佳，又因证券价格为高噪声序列，故难以对证券价格趋势的变动做出科学的、严谨的判断，而ANN容易处理不完整的、模糊不确定或规律性不明显、高噪声的数据，所以用ANN进行价格预测的优势是传统时间序列模型无法相提并论的。

长短期记忆人工神经网络（Long-Short Term Memory， LSTM）是人工神经网络的一种，衍生于循环人工神经网络（Recurrent Neural Network， RNN），因其具有负责计算时间序列中各个观测值之间依赖性的能力，所以，LSTM通常被用于预测目的[1]。又因其具有快速适应趋势中急剧变化的固有能力，所以，LSTM可以在波动的时间序列中很好地工作。传统的时间序列分析模型，如差分整合移动平均自回归模型 （Autoregressive Integrated Moving Average Model， ARIMA）则无法尽快适应证券价格的突然剧烈变动。

一个精确度高的时间序列分析模型对证券市场的价格进行分析和预测，将有助于国家对宏观经济政策的把控，也能为投资者带来极大的利润。本文将运用LSTM模型对证券价格进行时间序列分析，并分别以收盘价和以指数移动平均值均线 （Exponential Moving Average， EMA）价格进行采样，对比两个不同采样方式的误差率，评估两种采样方式的预测效果，为国家对市场的监督和投资者的决策提供参考。

1 LSTM模型原理

由于RNN模型没有长期记忆能力和会出现梯度爆炸或者梯度消失等弊端，在RNN模型的基础之上，Juergen Schmidhuber提出了LSTM模型。

LSTM除了RNN结构外，还具有阀门节点层。有三种类型的阀门：忘记门，输入门和输出门。这些阀门可以被打开或关闭，用于确定模型网络的内存状态（前一个网络的状态）的输出是否达到阈值，从而添加到该层的当前计算中。

ft，it，ot和Ct分别表示在t时刻对应的三种门结构和细胞状态;Wf，Wi，Wo和Wc表示循环层的权重矩阵;σ表示激活函数，一般为sigmoid函数或者tanh函数;bf，bi，bo和bc表示偏置向量，LSTM模型的计算公式如下[2]：

2 EMA均线原理

EMA均线是一种趋向类指标，其构造的原理是对收盘价进行算术平均，并且把不同时间的平均值连接成一条平滑的曲线，用于判断证券价格未来走势的变动趋势。对序列{xn}定义其截至第n项的周期为N的指数移动平均 EMAN（xn）的计算公式：

由于x1之前没有数据，一般都会补充定义x0=x-1=x-2=…=x1。这样自然就能给出EMAN（x1）=x1的结果。从定义式中，我们可以看出EMA均线加权平均的特性。在EMA均线指标中，时间越靠近当天（当期）时刻，该证券价格所获得的权重越大。这说明EMA函数对近期的证券价格逐步增加权重比，更能及时反映近期的证券价格的波动情况[3]。

3 模型构建

本文基于Python3.8和Tensorflow环境下的Keras API进行LSTM模型的搭建。

本文搭建的LSTM模型共有1层隐藏层，该隐藏层内含有的神经元数量为128个。

人工神经网络运用梯度下降法在反向传播过程中，迭代出最佳的损失残差，能更好地基于训练数据迭代地更新神经网络权重[4]。本文选用的梯度下降迭代器为Adam优化算法。

本文中选择用于衡量训练误差的损失函数为均方误差（Mean Squared Error， MSE）。训练过程中，随着迭代次数不断增加，MSE的值会不断缩小，当MSE的值越来越接近于0，说明LSTM模型拟合的效果越来越好[5]。

在对神经网络模型进行多次训练之后，发现Epochs次数为1000时，模型对数据拟合的损失函数MSE的值最小，即拟合的精确度最高，故本文所选用的Epochs次数为1000次，选用的输入数据批次大小 （Batch Size）为128，数据采样的滑动窗口设置为1。

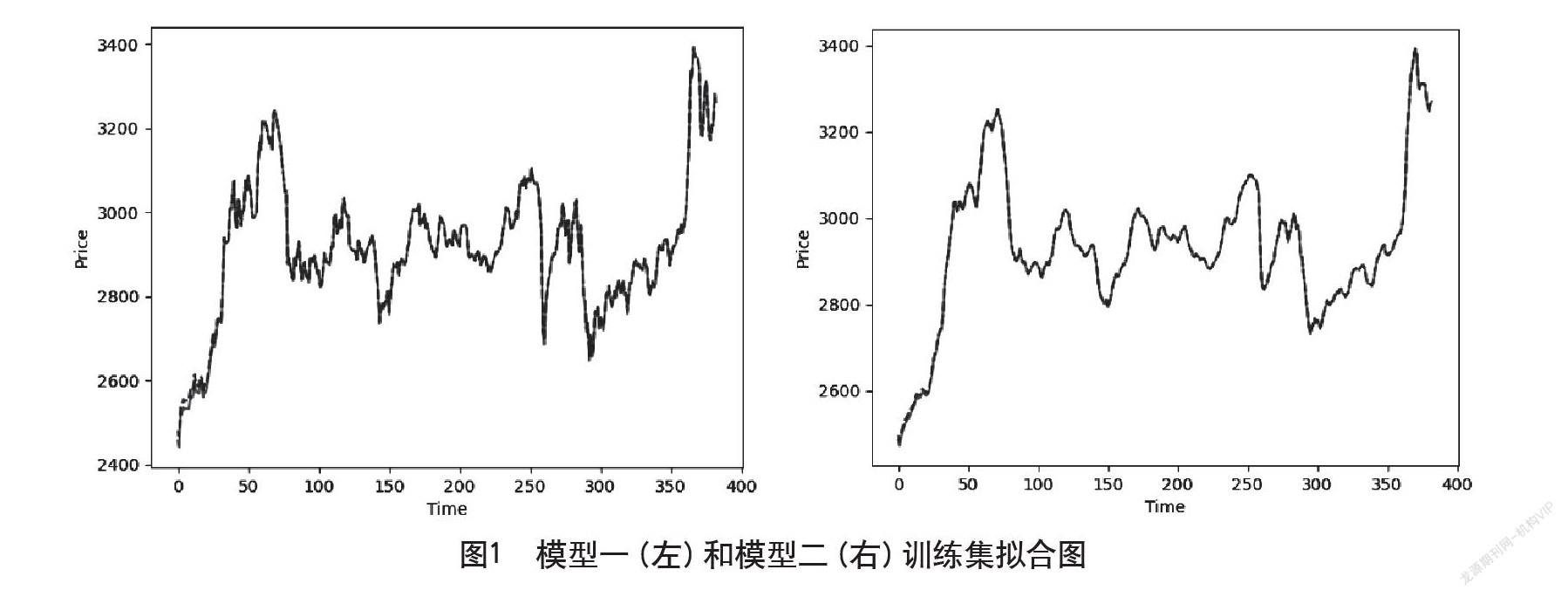
本文利用LSTM神经网络建立了两个不同的模型来进行证券价格的预测，具体模型描述如下：

模型一：利用连续采样单纯的历史收盘价作为模型的输入数据;

模型二：利用连续采用的历史收盘价的EMA价格作为模型的输入数据。