Stability and optoelectronic property of lead-free halide double perovskite Cs2B′BiI6(B′=Li,Na and K)∗

Yunhui Liu(刘云辉) Wei Wang(王威) Feng Xiao(肖峰) Liangbin Xiong(熊良斌) and Xing Ming(明星)

1College of Science,Guilin University of Technology,Guilin 541004,China

2School of Optoelectronic Engineering,Guangdong Polytechnic Normal University,Guangzhou 510665,China

Keywords: lead-free halide double perovskite,solar cells,stability,optoelectronic property

1. Introduction

Lead-based halide perovskites have revolutionized the development of solar cells in the past decade, achieving a conversion efficiency of more than 25%, which are superior to the polycrystalline silicon and thin-film photovoltaic solar cells.[1–3]Despite these impressive achievements, halide perovskites still face some unresolved disadvantages. The instability and toxicity of lead are obstacles to the industrial application of solar cells.[4–6]In order to solve these issues,it is significant to find stable and non-toxic perovskite alternates.[7,8]One simple strategy to obtain lead-free halide is replacing Pb2+cations with other less toxic divalent metal ions Sn2+or Ge2+in the same IV group.[9]Unfortunately,the materials containing Sn2+and Ge2+ions are often destabilized by the oxidation of divalent ions to their corresponding 4+states.[10]Another promising way is based on the replacement of two divalent Pb2+ions with one monovalentB′+and one trivalentB′′3+cation(2Pb2+→B′++B′′3+),generatingA+2B′+B′′3+X6(AandB′=Li,Na,K,Rb,Cs,Ag,Tl,etc.;B′′=Bi,Al,Ln,Ga, Fe, etc.;X=F, Cl, Br, I) compounds, named as double perovskite (DP), which maintain both the perovskite crystal structure and the charge neutrality.[11–18]

TheA+2B′+B′′3+X6DP materials can date back to the end of the 1960s, for example, Cs2NaBiCl6and Cs2KBiCl6have been synthesized for a long time, historically known as elpasolite with a face-center cubic structure and space group ofFm¯3m.[19]The ferroelastic and ferroelectric phase transitions in elpasolites have attracted intensive attentions,while they have never been considered for photovoltaic applications at that time.[19–21]The Raman spectrum of Cs2NaBiCl6indicates that the structures of the BiCl6and NaCl6are (nearly) octahedra.[22]The low-temperature lattice instability of Cs2NaBiCl6is ascribed to the Cs+hole size.[23]In view of the tremendous interest in halide perovskites,the experimentally already synthesized all-inorganic halide DPs Cs2B′BiX6, such as Cs2AgBiCl6, Cs2AgBiBr6,Cs2NaBiCl6, and Cs2NaBiCl6have received widespread attention recently.[17]Owning to good stability under ambient conditions, suitable band gap values, and excellent optical absorption at the visible-light range, the Cs2AgBiCl6and Cs2AgBiBr6have been put forward as promising alternatives to the lead halide perovskites in 2016.[24–26]Alternatively,Cs2NaBiCl6possesses an indirect band gap of 3.41 eV and shows adjustably photoelectric properties by various ion doping.[27–30]A bright orange-red phosphor has been achieved by doping Mn2+ions into Cs2NaBiCl6host, and a red shift of the optical absorption and excitation spectra has been observed through further chemical substitution of Cl−ions with Br−ions.[28]The indirect band gap can change to direct one by gradual substitution of Bi3+with In3+in Cs2NaBiCl6, and a strong orange-yellow photoluminescence was observed when doped with Mn2+, and can be manipulated by the Bi3+/In3+ratios.[29]In addition,Cs2NaBiCl6nanocrystals with different concentrations of doped ions have been synthesized, which show the excitonic absorption energy shifting from 3.82 eV to 3.48 eV by Ag+ions doping, leading to a significant improvement of photoluminescence quantum yield from 1.7%to 20%.[30]

Recently,another novel halide DP material of Cs2NaBiI6has been synthesized for the first time by hydrothermal reaction.[31]Cs2NaBiI6possesses a proper band gap of 1.66 eV,high stability in ambient air,and excellent optical absorption performances,which fulfil the requirements of photovoltaic applications. Cs2NaBiI6has been successfully applied into a solar cell device, which simultaneously solves the key issues of toxicity and stability of the lead-based halide perovskites. Furthermore, compared with the wider band gap of Cs2NaBiCl6,the iodide Cs2NaBiI6points out a promising direction to reduce the band gap of the halide DP materials.[32]High quality Cs2NaBiI6films have been obtained by vacuum evaporation, which dramatically enhances the photovoltaic performance by post-treatment engineering.[33]Different from the cubic structure of the common DP materials [Fig. 1(a)],the x-ray diffraction pattern of Cs2NaBiI6powder is consistent with that of the MA2AgBiI6, which crystallizes in an orthorhombic structure.[31,34]However,detailed crystal structure information has not been reported in these pioneer works.

First-principles calculations have been extensively employed to design a series of halide DPs,[7,8,11–18]assess the stability of the DPs,[35]and explore the electronic and optical properties of DPs.[36,37]Based on a hypothetical cubic DP structure, the calculated formation enthalpy of the cubic phase Cs2NaBiI6is positive,[38]indicating it is thermodynamically unstable,which is obviously contradictory with the experimental fact. As shown in Fig. 1(a), mostA+2B′+B′′3+X6DPs adopt the rock salt sublattice as the ground state, theB′X6andB′′X6octahedra alternate in all directions.[11]In addition,the halide perovskites often crystallize in other three typical structures,tetragonal,orthorhombic,and hexagonal phases[Figs.1(b)–1(d)].[39,40]Undoubtedly,it is deserving to identify the true crystal structure of Cs2NaBiI6,and it is significant to seek other similar iodide DPs to Cs2NaBiI6. In this paper,we evaluate the stability and explore the electronic structures and optical properties of a series of iodide Cs2B′BiI6(B′=Li,Na and K) DP materials by first-principles calculations. These theoretical results provide a useful guide for the development of lead-free DP materials.

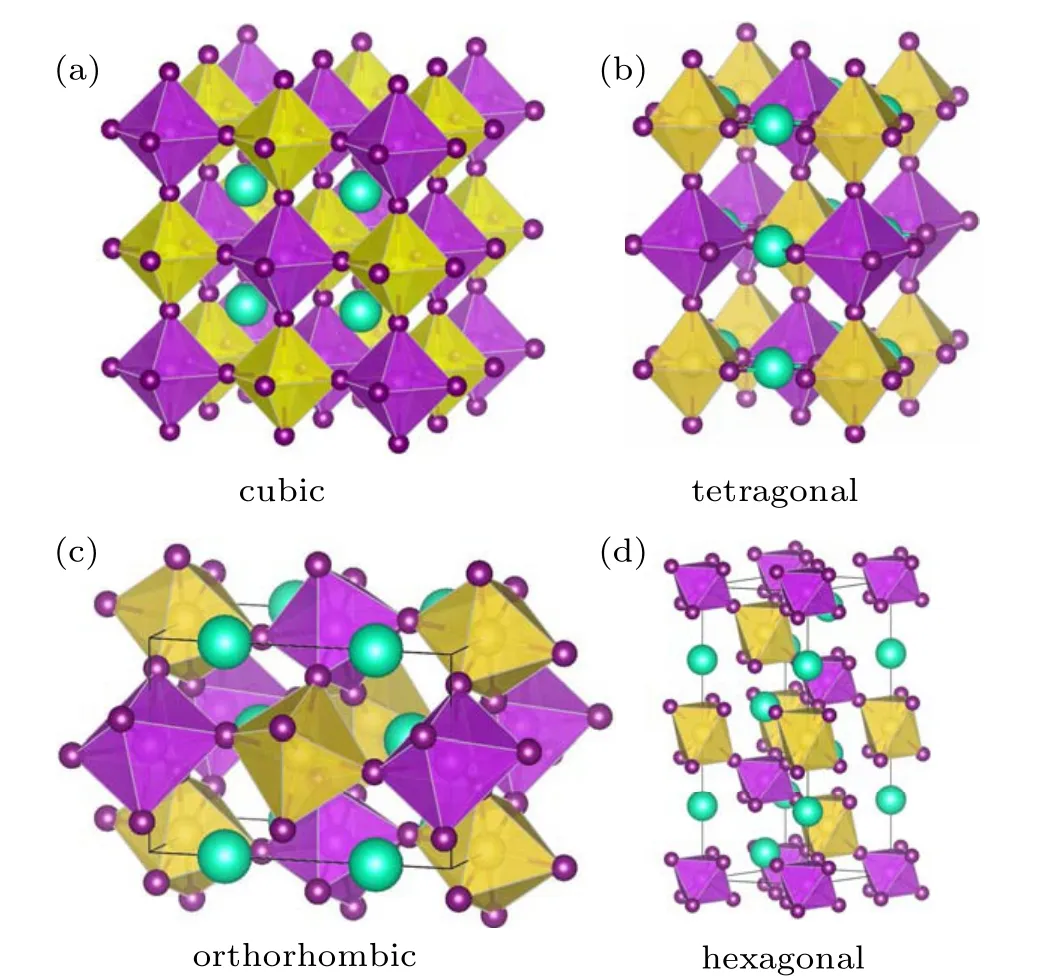
Fig.1. The schematic crystal structure of hybrid halide A+2 B′+B′′3+X6 DPs with different structural symmetry: (a)cubic,(b)tetragonal,(c)orthorhombic,and(d)hexagonal. The cyan,yellow,magenta,and purple balls denote the A,B′,B′′,and X atoms,respectively. The B′X6 and B′′X6 octahedra are depicted in yellow and magenta colors.

2. Computational methods

All the theoretical calculations are based on the density functional theory as implemented in the Viennaab initiosimulation package(VASP)program[41]within the projector augmented wave method.[42]All calculations are performed by using the generalized-gradient approximation(GGA)electron exchange-correlation functional of Perdew–Burke–Ernzerhof(PBE)form.[43]The cutoff energy of 520 eV is used,and thekmesh is set to 0.15/2π°A−1in reciprocal space. Electronic structures and optical property calculations have considered the spin-orbit coupling (SOC) effects. The structural models of Cs2B′BiI6were initially built up by replacing atoms of the halide perovskite MAPbI3materials. As shown in Fig.1,the cubic,tetragonal,orthorhombic,and hexagonal phases are considered in our simulations. The calculations are performed on primitive cells. All the lattice parameters and atomic positions of each DP compositions are fully relaxed until the force on each ion is less than 0.001 eV/°A and total energy convergence to 10−6eV.

The optical absorption spectrum is calculated by the energy-related dielectric function:[44]ε(ω)=ε1(ω)+iε2(ω),whereε1(ω)andε2(ω)are the real and imaginary parts of the dielectric function, respectively. The optical absorption coefficientα(ω)can be calculated by the following formula:[45]

whereωis the optical frequency, andcis the light speed in vacuum.

3. Results and discussion

3.1. Geometric stability

In order to evaluate the crystallographic stability of the perovskite materialsABX3, two empirical parameters in the framework of the idealized solid sphere model are usually considered,that is the Goldschmidt tolerance factortand the octahedral factorµ.[46]The Goldschmidt tolerance factortis a commonly used and most successful empirical criteria,which is expressed as follows:[47]

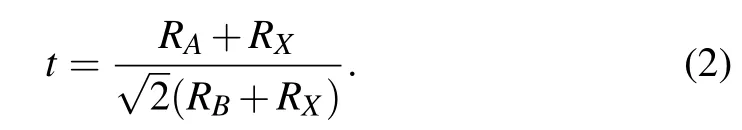
The octahedral factorµis defined asµ=RB/RX.RA,RB,andRXare the effective ionic radii of theAcations,Bcations,andXanions,respectively.Considering two types ofBcations(B′andB′′)in theA2B′+B′′3+X6DPs,the average value of the cation radius ofB′andB′′is used asRB. In general, the stable ranges of the DPs are 0.813 ≤t≤1.107 and 0.414 ≤µ≤0.732.[48]

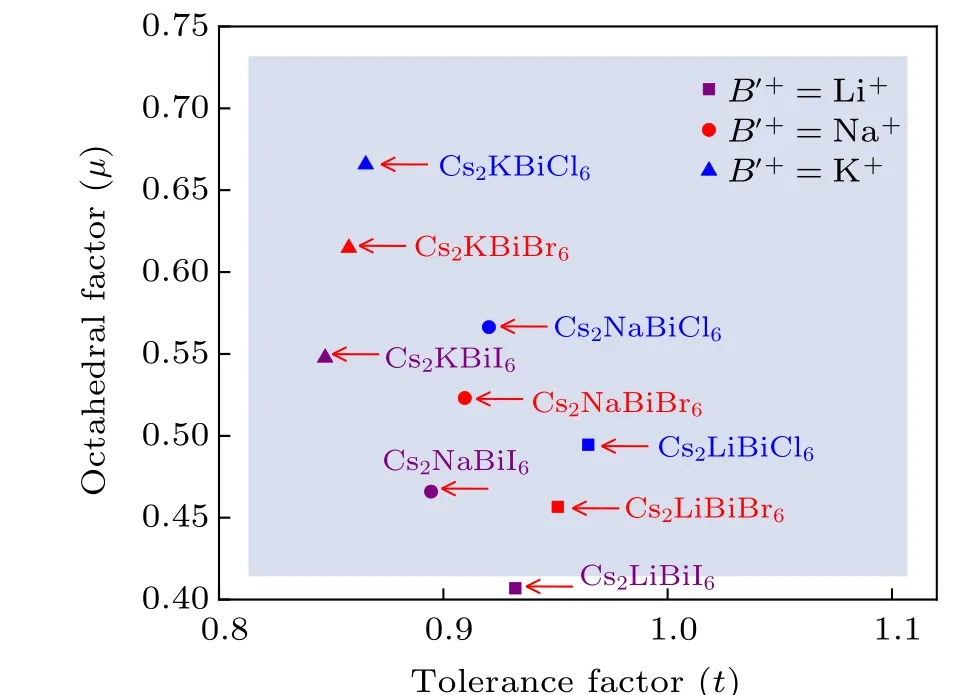
Fig.2.Tolerance factor–octahedral structure map of the Cs2B′BiX6(B′=Li,Na and K,X =Cl,Br,and I)DPs with effective tolerance factor(t)and octahedral factor(µ)as variables.

Using the Shannon ionic radii of the 12-coordinated Cs+ions and 6-coordinatedB′+, Bi3+, andX−ions,[49]we calculate thetandµfactors of the Cs2B′BiX6(B′=Li, Na and K;X=Cl,Br and I)DPs. Figure 2 shows the distribution of the candidate Cs2B′BiX6DPs in the map withtandµvariables. The shaded area indicates that the geometric structures of the DPs are stable.All the Cs2B′BiX6DPs except Cs2LiBiI6fall in the empirically stable region of DPs. Theµfactor of Cs2LiBiI6is 0.407, which is on the verge of the stable range ofµ. Furthermore,theµfactors of the LiBr6and LiI6octahedra are 0.388 and 0.346, which are out of the stable criterion ofµ. These results illustrate that Cs2LiBiBr6and Cs2LiBiI6are structurally less stable relative to other Cs2B′BiX6DPs.In fact, among these predicted stable Cs2B′BiX6DPs, only Cs2NaBiCl6, Cs2KBiCl6, and Cs2NaBiI6have been experimentally synthesized to date.[19,20,22,23,31]As pointed out by Liet al.,both thetandµfactors are necessary but not sufficient conditions for the halide perovskite formability.[48]Therefore,it is necessary to assess the stability of Cs2B′BiI6DPs based on other aspects.

3.2. Thermodynamic stability

We evaluate the ground state of the four possible structures of Cs2B′BiI6by calculating the total energy(see Table 1).The calculated results manifest that the most favorable structure of Cs2B′BiI6is the orthorhombic phase from an energetic viewpoint, which agrees with the experimental fact that the orthorhombic structure Cs2NaBiI6has been synthesized.[31]

Table 1. The calculated total energy E (in units of eV/formula)of the four candidate structures of Cs2B′BiI6 DPs.

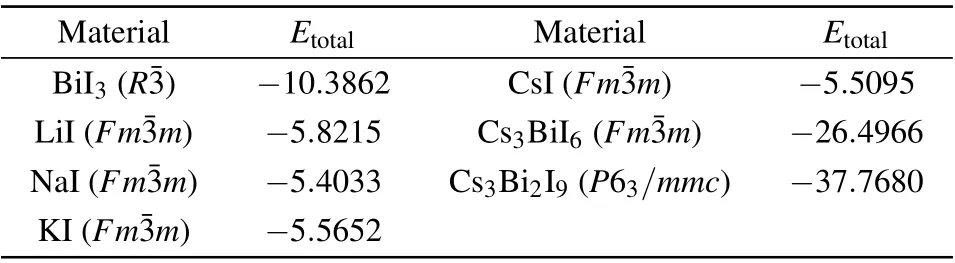
Table 2.Calculated total energy Etotal(eV/formula)of the reactants and decomposition products of the Cs2B′BiI6 DPs. The most stable crystal structures(the corresponding space groups are given in the parentheses)from the Materials Project crystal structure databases[50] are employed to calculate Etotal of these materials.

The formation energy of the cubic,tetragonal,orthorhombic,and hexagonal phases Cs2B′BiI6DPs are shown in Fig.3.The orthorhombic phase Cs2B′BiI6displays negative formation energies, while all the other phases Cs2B′BiI6DPs show positive formation energies. Therefore, only the orthorhombic phase meets the thermodynamic stable conditions,and the other three crystal structures are unstable. The theoretically calculated result is in line with previous reports on the cubic phase Cs2NaBiI6.[38]Considering the Cs2NaBiI6has been experimentally synthesized in the orthorhombic structure,[31]we suspect that orthorhombic Cs2LiBiI6and Cs2KBiI6can also be synthesized by the corresponding binary compounds within an exothermic reaction process.

The calculated results of the decomposition enthalpy of Cs2B′BiI6along two representative decomposition paths are shown in Fig.4. The products of the first decomposition path are Cs3Bi2I9, CsI andB′I, while those of the second case are Cs3BiI6, BiI3andB′I. The ∆H1are all negative values for all the four considered phases, which indicate that even if the Cs2B′BiI6DPs have been synthesized, they will spontaneously decompose to Cs3Bi2I9and other binary compositions. By contrast, all the DPs except the tetragonal phase show positive ∆H2values, illustrating that other three phases of Cs2B′BiI6DPs will much more stable than the tetragonal phase. All the orthorhombic phases show lower values of ∆H1and higher values of ∆H2, which is consistent with the results of the formation energy, so that the orthorhombic phase will more stable than other three crystal structures.In addition,the orthorhombic phase of Cs2LiBiI6exhibits the largest negative value of ∆H1and the smallest positive value of∆H2with respect to the same orthorhombic phase Cs2NaBiI6and Cs2KBiI6, indicates that orthorhombic Cs2LiBiI6is less stable relative to other two counterpart DPs. The thermodynamic stability is well consistent with the geometric stability,so that the stable orthorhombic Cs2B′BiI6DPs may be synthesized in experiments.[31]Hereafter, we will only discuss the orthorhombic phase Cs2B′BiI6.

Owing to the orthorhombic structures of Cs2B′BiI6are constructed from the MAPbI3by replacing MA group with Cs ions and Pb ions withB′and Bi ions,[31,34]the spatial symmetry ofB-site Pb ions have split to two differentB′and Bi ions,which form the rock-salt order in the perovskiteBsites.Then the orthorhombic space groupPnmaof MAPbI3formally changes to the monoclinic space groupP21/n.[51]The Wyckoff positions of Bi andB′(B′=Li, Na, K) are 2c(0.5,0.5, 0) and 2d(0, 0, 0), which have unchanged in the monoclinic representation. The Cs and I atoms occupy the Wyckoff positions of 4e. The crystallographic data of the orthorhombic Cs2B′BiI6DPs are shown in Table 3. TheB′–I (B′=Na or K)bond lengths are longer than those of the Bi–I bond length.Other lead-free DPs also have similar bond lengths, for instance,Cs2AgSbCl6(Ag–Cl=2.72 °A;Sb–Cl=2.63 °A).[52]

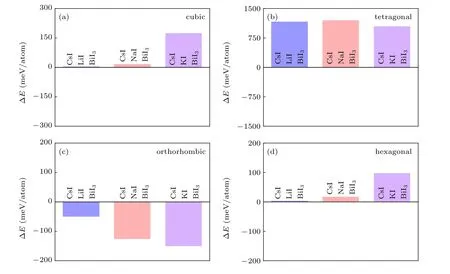
Fig.3.Calculated formation energy of the Cs2B′BiI6 DPs with different crystal structures:(a)cubic,(b)tetragonal,(c)orthorhombic,(d)hexagonal.The blue,orange and purple bars represent the result of Cs2LiBiI6,Cs2NaBiI6 and Cs2KBiI6,respectively.

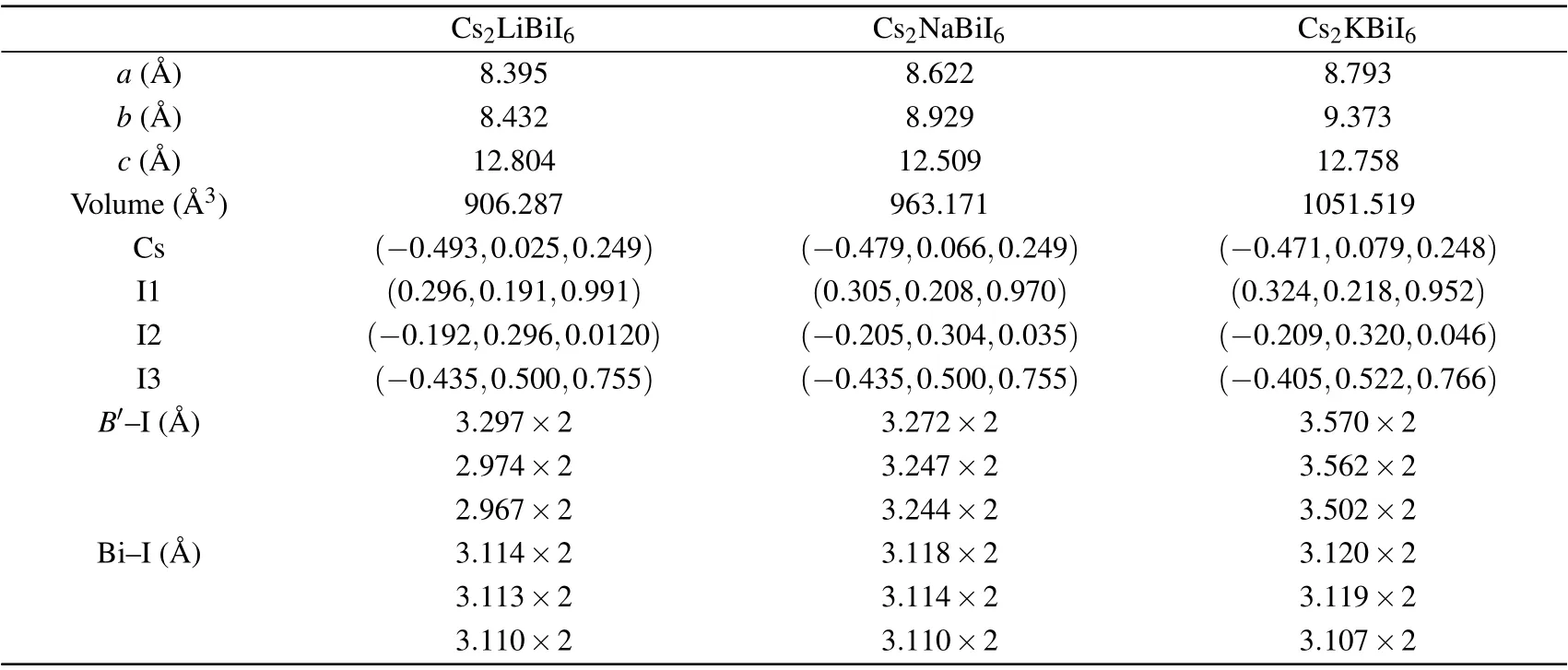
Table 3. Calculated lattice parameters,atomic positions,cell volumes and bond distances(B′–I and Bi–I)of Cs2B′BiI6 DPs.

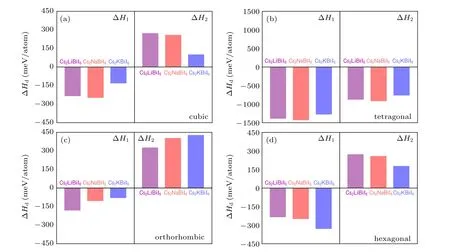
Fig.4. Calculated decomposition enthalpy ∆Hd of Cs2B′BiI6 double perovskites along two representative decomposition pathways: (a)cubic,(b)tetragonal,(c)orthorhombic,and(d)hexagonal.

3.3. Mechanical stability

Elastic constants are important parameters to measure the bearing capacity of materials, and could conduce to evaluate the mechanical stability. In this study, the elastic constantsCijare estimated in accordance with the relationship between strain and volume,[53]which are listed in Table 4. According to the mechanical stability criterion of monoclinic crystals,[54]Cs2LiBiI6material does not meet the mechanical stability,while Cs2NaBiI6and Cs2KBiI6fulfil the mechanical stability conditions. Therefore,the geometric,thermodynamic,and mechanical stabilities reveal that the orthorhombic Cs2LiBiI6material is less stable relative to the isostructural Cs2NaBiI6and Cs2KBiI6DPs.

Employing the Voigt–Reuss–Hill approximations, the mechanical properties, such as the bulk modulus (B) and the shear modulus (G) can be calculated from the elastic matrixCi j,[55,56]while the Young’s modulus (E) and Poisson’s ratio (ν) are calculated by the following formula:E=9BG/(3B+G),andν=(3B−G)/[2(3B+G)].[54]The small bulk moduliBmanifest that the Cs2B′BiI6are easily compressible materials, which are also easier to be deformed by tensile stress for the reason of the weak bond strength. Furthermore, the shear moduliGof Cs2B′BiI6are smaller with respect to Cs2AgBiI6,[57]and indicates its stronger capacity to shape change through distortion under shear loading. The calculated Poisson’s ratios are bigger than 0.3,and the Pugh’s ratiosB/Gare larger than the critical value of 1.75,which means these Cs2B′BiI6DP materials possess good ductility. The mechanical properties demonstrate that the Cs2B′BiI6DPs may be used as flexible materials.[57]

Table 4. Calculated elastic constants Cij (GPa), bulk modulus B (GPa), shear modulus G (GPa), Young’s modulus E (GPa), Poisson’s ratio ν,Pugh’s ratio (B/G) of Cs2B′BiI6. The subscripts V and R of the moduli denote results from the Voigt and Reuss models, while B and G moduli without subscripts from the Voigt–Reuss–Hill approximations defined as the average of the Reuss and Voight values,respectively.

3.4. Electronic structure and optical properties

In order to better understand the electronic structure of the Cs2B′BiI6, the band structure and the partial density of states(DOS) have been calculated. The band gaps of Cs2LiBiI6,Cs2NaBiI6and Cs2KBiI6calculated within GGA are 2.26 eV,2.37 eV, and 2.79 eV, respectively. By considering the SOC effect, the band gaps are significantly reduced to 1.51 eV,1.73 eV and 1.99 eV,respectively The theoretically calculated band gap value (1.73 eV) of Cs2NaBiI6agrees well with the experimentally derived value(1.66 eV).[31]Without considering the SOC effect,Cs2B′BiI6DPs are predicted to be indirect band gap semiconductors. As shown in Fig. 5, Cs2LiBiI6is predicted to be a direct band gap semiconductor when the SOC effect has been considered,where the valence band maximum(VBM)and the conduction band minimum(CBM)are located at the sameΓpoint. By contrast, Cs2NaBiI6and Cs2KBiI6still are indirect band gap semiconductors. The band gap values of Cs2B′BiI6increase in the order of increasing ions radium from Li,Na to K,which are similar to the cases of chloride Cs2B′BiCl6DPs.[11]At the same time,the increasing size ofB′ion from Li, Na to K will lead to theB′I6octahedron expand and the BiX6octahedron contract, which result in an increase of the interaction between Bi 6p and I 5p orbitals and lead to a raise of VBM.As shown in the partial DOS,the VBM predominantly arise from the I 5p orbital, while the CBM is contributed by strong hybridizations of Bi 6p and I 5p states.Furthermore,the strong SOC interactions induced energy level splitting of the Bi 6p states will give rise to the decrease of the CBM position and the reduction of the band gap. Replacing Cl by I significantly lower the CBM and raise the VBM due to the interaction between Bi3+and I ions,[11]resulting in the band gap shrinkage from 3.41 eV(Cs2NaBiCl6)[29]to 1.66 eV(Cs2NaBiI6).[31]

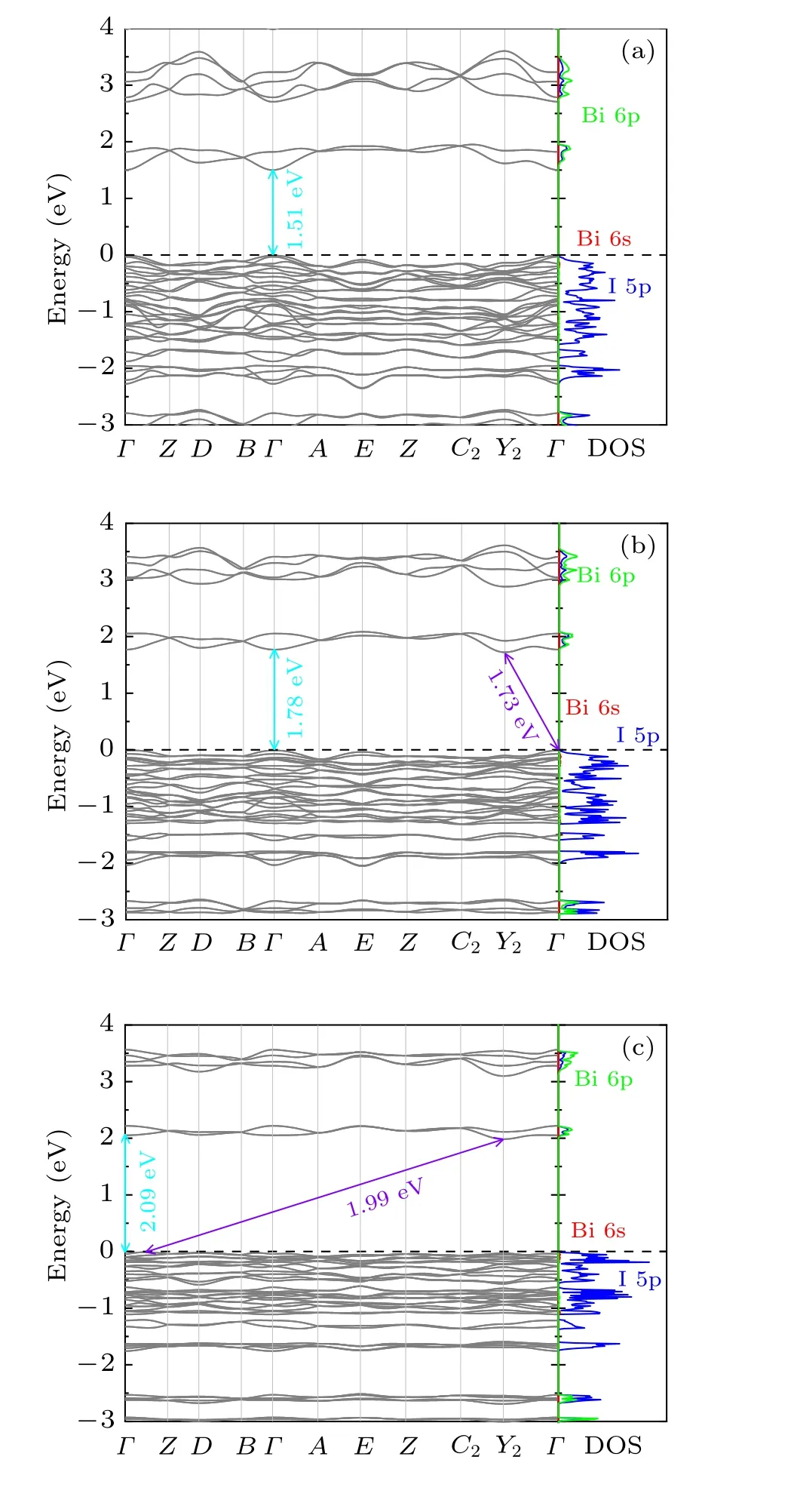
Fig. 5. Band structures and the partial DOS of orthorhombic Cs2B′BiI6 DPs calculated within GGA + SOC: (a) Cs2LiBiI6, (b) Cs2NaBiI6,(c) Cs2KBiI6. The arrows depict the direct and indirect band gaps. The partial DOS of the Bi 6s,6p,and I 5p states are drawn with red,green,and blue lines,respectively.

Table 5. The effective masses of electrons(m∗e)in CBM and holes(m∗h)in VBM,reduced effective masse of the carriers(m∗r),static dielectric constant(εoptic)and exciton binding energy(Eb)of Cs2B′BiI6.

As shown in Table 5, the effective masses of electrons(holes)of Cs2LiBiI6,Cs2NaBiI6,and Cs2KBiI6are 0.6272me(1.9149me), 0.7578me(2.9023me), and 1.2658me(3.2976me), respectively, wheremestands for the electron static mass. The effective masses of electrons and holes increase along with the increasing atomic radius, implying lower carrier mobility,because the effective mass and conductivity show an inverse proportional relationship.[60]The exciton binding energies of Cs2LiBiI6(Cs2NaBiI6, Cs2KBiI6)are 0.2321 eV (0.3025 eV, 0.5775 eV), which are comparable to those of the low-dimensional organic tin bromide perovskites[37]and 3D/2D hybrid lead-halide perovskites(C4H9NH3)2PbX4.[58]These results imply that Cs2B′BiI6DPs materials with weaker exciton binding energy are suitable for solar cell applications.

To further investigate the light harvesting capacity of these Cs2B′BiI6DPs, we calculate the optical absorption coefficients. As shown in Fig. 6, the light absorption of Cs2LiBiI6(Cs2NaBiI6, Cs2KBiI6) increases rapidly above 1.51 eV (1.73 eV, 1.99 eV), which are consist with the band gap determined by electronic transitions from the top of valence bands to the bottom of conduction bands. Especially,the light absorption efficiency is significantly improved in the visible light region,which reaches an order of 106cm−1,overperforms the organic–inorganic hybrid perovskite materials MAPbI3.[61,62]The characteristic peaks of absorption coefficients are mainly derived from the transitions from I 5p to Bi 6p states, similar to that of the lead halide perovskites.According to the band dispersions illustrated in Fig. 5, although the band gaps of the Cs2NaBiI6and Cs2KBiI6are indirect type, the energies of the conduction bands are very close atΓandY2points, implying strong direct transitions,which are beneficial for the optical performances. In addition,the absorption coefficients along three incident directions are very close, implying the Cs2B′BiI6DPs are almost isotropic.The excellent optical absorption performances demonstrate Cs2B′BiI6DPs can be effective solar energy absorbers in the visible light spectrum.

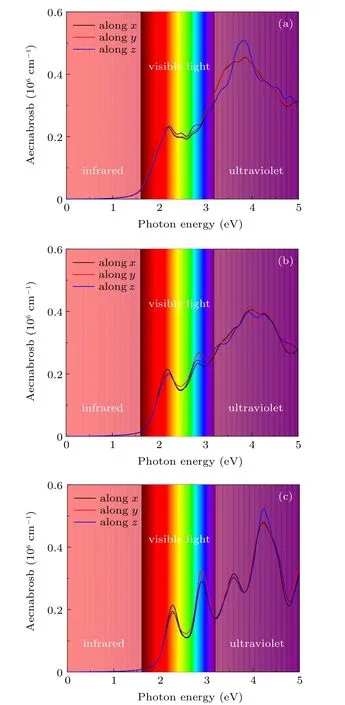
Fig. 6. Optical absorption spectrum of orthorhombic Cs2B′BiI6:(a)Cs2LiBiI6,(b)Cs2NaBiI6,(c)Cs2KBiI6.

4. Conclusions

In summary, the geometric stability, thermodynamic stability, mechanical stability, electronic structure, and optical properties of the Cs2B′BiI6(B′= Li, Na and K) DPs were studied by the first-principles calculations. By comprehensive evaluations of the tolerance factort, octahedral factorµ, formation energy, decomposition enthalpy, and mechanical stability, the stable orthorhombic phase of Cs2B′BiI6has been identified out of four different crystal structures(cubic,tetragonal,orthorhombic,and hexagonal phases). Furthermore,the orthorhombic Cs2LiBiI6is less stable than the isostructural Cs2NaBiI6and Cs2KBiI6, which is consistent with the experimental fact that the orthorhombic structure Cs2NaBiI6has been synthesized. The orthorhombic Cs2LiBiI6show direct band gap characteristics,while Cs2NaBiI6and Cs2KBiI6have indirect band gaps,and all of them show weaker exciton binding energies and good light absorption performances in the visible light region.According to the good stability,suitable band gap,and excellent optoelectronic properties,the orthorhombic Cs2NaBiI6and Cs2KBiI6can be used as promising lead-free solar-cells materials for optoelectronic applications.