地下水不同盐度条件潜水蒸发特性及其简化模型适用性评价

茹秋瑾， 杨军超， 李晓琳,3,4

(1.杨凌职业技术学院， 陕西 杨凌 712100； 2.陕西省引汉济渭工程建设有限公司，陕西 西安710010； 3.西安理工大学水利水电学院，陕西 西安 710048； 4.西北旱区生态水利国家重点实验室，陕西 西安 710048； )

1 研究背景

地下水是一种重要水资源，在地下水浅埋区，地下水通过毛管上升对包气带的补给作用明显，且毛细水上升可以用来描述地下水的补给量，潜水蒸发在农田水循环中发挥着重要作用，在农田水利领域备受重视[1-3]。在地下水位较高地区，地下水中的可溶性盐在蒸发作用下随土壤水向上迁移，并在土体中聚集，增加了土壤盐渍化风险，危害作物生长，成为制约农业可持续发展的障碍[4-5]。潜水蒸发与土壤盐分积累和土壤盐渍化密切相关，开展浅埋区潜水蒸发特性的研究对制定灌溉制度和淋洗农田盐分均具有重要的实践意义。

已有的关于潜水蒸发特性的研究成果多集中于淡水地下水[6-9]，在一定程度上忽略了地下水为盐水的情况，然而在地下水浅埋干旱地区，地下水中往往存在盐分，这些盐分很可能改变潜水蒸发规律，有关地下水含盐情况下的毛细水上升和潜水蒸发特性亟需探索。科学评价潜水蒸发对土壤盐渍化研究、地下水数值模拟参数反演、地下水循环研究以及地下水资源科学评价与管理均发挥着重要作用[10]。目前，较为常用的潜水蒸发计算方法主要有蒸渗仪直接测定法和经验公式法，农田实测法中蒸渗仪尺寸和材料的选择往往对观测精度具有明显影响，而经验公式法缺乏理论支撑，不利于其机理研究。基于土壤水动力学理论的极限蒸发强度(Emax)模型计算方法将地下水蒸发看作蒸发条件下的非饱和土壤水运动问题，当大气蒸发能力趋于无穷大时，潜水蒸发强度则趋于Emax[11]，可用Gardner模型进行估算。但采用该方法计算导水率(即K=a/(sn+b))时，通常忽略常数b以实现模型简化的目的，虽然模型得以简化，但在很大程度上将影响Emax的估算精度，关于忽略参数b如何影响Emax估算精度、简化模型是否可靠等问题并未引起广泛关注。

本研究选用最为常见的K-Cl和Na-Cl型盐溶液作为供水水源，以陕西杨凌、长武地区和山东临沂地区壤土为例，开展毛细水上升和潜水蒸发试验，对不同地下水盐度条件下的毛细水上升和恒定埋深潜水蒸发特性进行研究，并基于土壤水动力学理论采用Gardner模型对Emax进行估算，进一步对该模型中参数b对Emax估算精度的影响进行评价，进而评判在Emax估算问题中Gardner模型是否可以简化。该研究可为农田盐碱化防治提供理论依据。

2 资料来源与研究方法

2.1 供试材料

供试土样取自陕西杨凌(YL)、陕西长武(CW)、山东临沂(LY)地区农田0～30 cm耕作土层，采集完成后充分混合。全部土样经风干、磨碎、去除杂质后过2 mm筛分，采用激光粒度仪测定土壤颗粒组成(表1)，全部供试土样均为非盐碱土。为探究盐溶液供水条件潜水蒸发特性，并根据微咸水(盐浓度1～3 g/L)、咸水(盐浓度3～10 g/L)和盐水(盐浓度10～50 g/L)矿化度范围，选用浓度为1、5、30 g/L的KCl和NaCl溶液分别作为供水水源(分别记作处理K-1、K-5、K-30、Na-1、Na-5、Na-30)并以蒸馏水作为对照组(记作处理CK)。

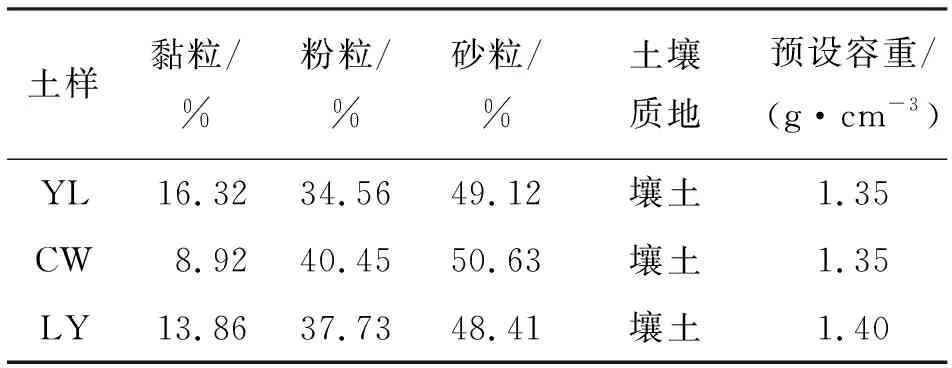
表1 供试土样颗粒组成

毛细水上升试验装置和恒定地下水浅埋条件潜水蒸发试验装置主要包括有机玻璃土柱(高60 cm，内径15 cm)、有机玻璃管(内径2.9 cm)、马氏瓶、灯泡等。

2.2 试验设计与方法

毛细水上升试验：将供试土样按预设容重装入有机玻璃管中，装土高度为30 cm，并在底部用纱网包裹，固定于铁架台，底端放入与供水水源连通的水槽内(见图1(a))。记录湿润锋到达顶部所需的时间T。由于管径远大于土壤粒径，故忽略管径对毛细作用的影响，可认为毛细水上升仅由毛管作用所致。各处理均进行3次重复。

定水位潜水蒸发试验：将供试土样按设定容重装入有机玻璃中形成土柱，并在土柱底部设10 cm厚砂石反滤层；将不同类型和浓度的盐溶液盛于马氏瓶中，马氏瓶与土柱底部连通以实现持续供水，供水水头恒定为50 cm(见图1(b))。当湿润锋上移至土样表面且毛细上升水稳定时，移除土表覆盖的塑料薄膜，并将土柱置于275 W远红外灯下(土样表面距光源垂直距离为40 cm)，昼夜蒸发试验持续20 d，每日8:00读取马氏瓶内水位刻度以计算日潜水蒸发量。各处理均进行3次重复。

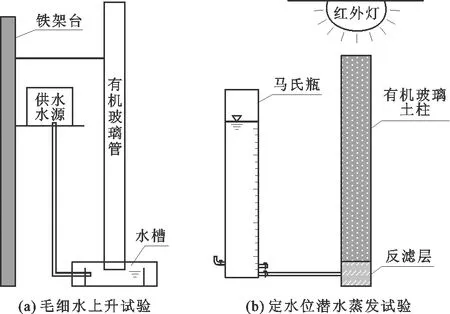
图1 毛细水上升与潜水蒸发试验装置示意图

2.3 模型构建

对于某种均质土壤，潜水位埋深为H，当处于稳定蒸发时，土壤含水率和吸力分布如图2所示。

图2 均质土壤稳定蒸发时含水率和吸力分布示意图

此时地表处的蒸发强度与任一断面处的土壤水通量相等，即为潜水蒸发强度，其定解问题可用公式(1)描述。

(1)

式中：E为潜水蒸发强度，cm/d；K(s)为导水率，cm/d；s为土壤水吸力，cm；z为垂直坐标(自地下水位起向上为正)，cm。

Gardner导水率计算公式为[12]：

(2)

对公式(1)进行积分，同时结合公式(2)，则z可表示如下：

(3)

式中：a、b、n均为常数，其中n值可为1.0、1.5、2.0、3.0、4.0，土质越粗则n值越大。

将z=H代入公式(3)中，便可获取地表处的土壤水吸力sH与稳定蒸发强度E的关系，如公式(4)所示。

(4)

由公式(4)可知，当H一定时，E随着sH的增大而增大；当地表处土壤风干时，sH则趋于无穷大，此时E将达到最大可能值。由于稳定蒸发强度即为定水位下的潜水蒸发强度，故可将稳定蒸发强度的最大可能值Emax定义为潜水极限蒸发强度[13]。

对于本研究中所供试的均质土样，取n=2[14]；当sH趋于无穷大时，可分别构建出忽略参数b(简化模型)和未忽略参数b时的Gardner模型，分别如公式(5)、(6)所示。

Emax=2.46aH-2

(5)

(6)

3 结果与分析

3.1 不同地下水矿化度对毛细水上升的影响

水分蒸发的内在驱动力为土壤毛管作用，故需评价地下水类型和矿化度对毛细水上升的影响。湿润锋到达土壤表面所需要的时间T可以反映蒸发强度，即时间T越短，则毛管作用越强，在外部环境相同条件下其蒸发强度越高。通过试验得出，对于YL、CW和LY土样的CK处理，T分别为396、388和410 min，均大于盐溶液供水处理；在地下水矿化度为1～30 g/ L范围内，KCl和NaCl处理的T值均表现为随浓度增加而增加。表明土壤水中KCl和NaCl会在一定程度上增强毛管作用，加快水分上升，使得在外部条件相同时的蒸发强度增强。

3.2 不同地下水矿化度对Emax的影响

试验中在持续光照和恒定埋深条件下，历时20 d后各处理潜水蒸发强度趋于稳定并达到最大值，各土样不同处理的潜水极限蒸发强度测定值与计算值如表2所示。

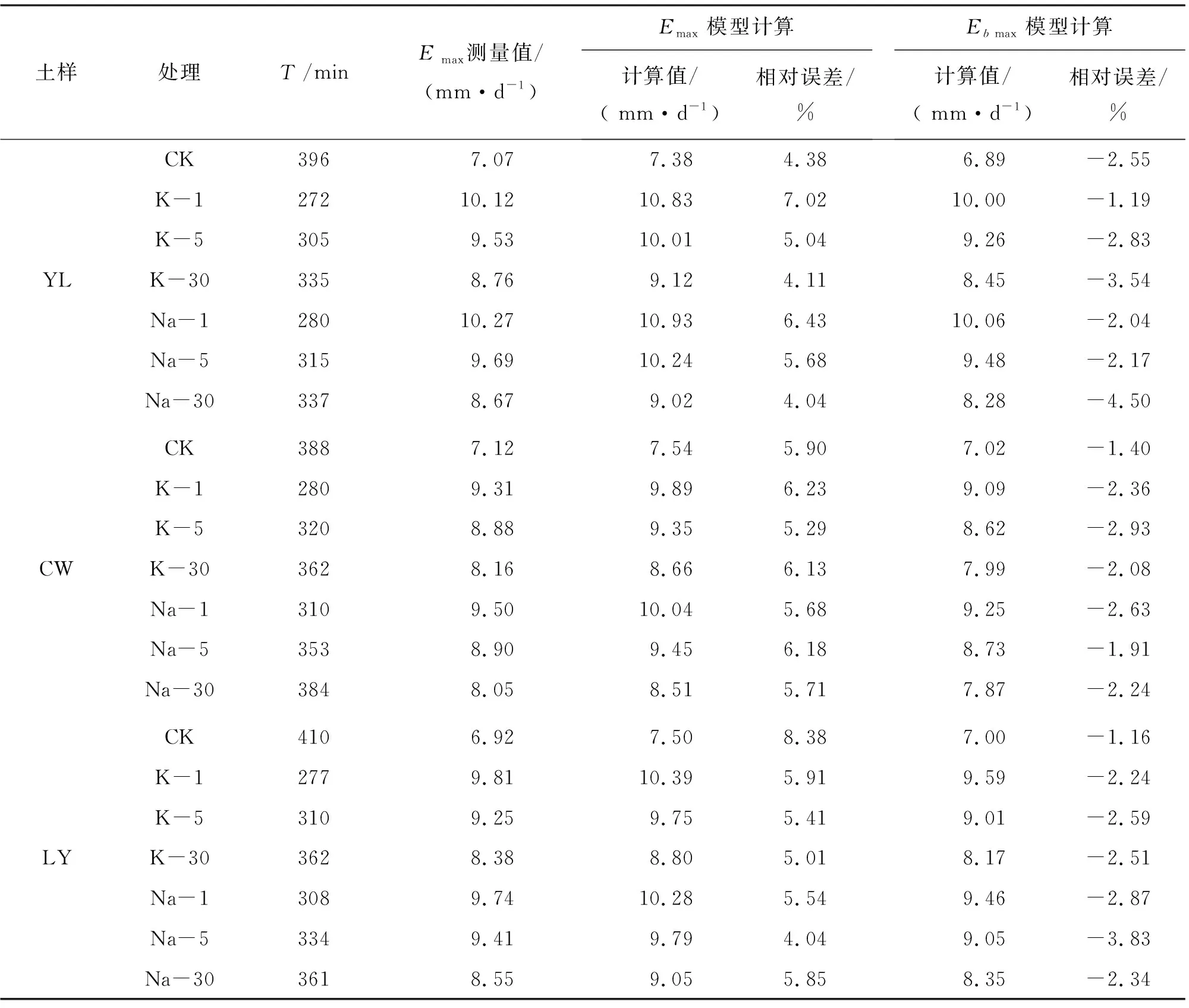
表2 各土样不同处理的潜水极限蒸发强度测定值与模型计算值

由表2中可看出：(1)Emax受溶质类型和浓度共同影响，进而导致不同溶质和浓度处理的Emax存在一定差异；对于YL、CW和LY土样的CK处理，Emax分别为7.07、7.12和6.92 mm/d，且均小于盐溶液供水处理；在地下水矿化度1～30 g/L范围内，KCl和NaCl处理的Emax值均表现为随浓度增加而减小。(2)采用Gardner模型对Emax进行估算时，在忽略和未忽略参数b(公式(5)、(6))两种情况下，Emax估算结果与其观测结果表现出相同的变化趋势；与实测值相比，忽略参数b导致Emax高估，考虑参数b导致Emax低估，Emax计算值与测量值之间的相对误差介于4.04%～8.38%，Eb max计算值与测量值之间的相对误差介于1.16～4.50%，表明采用考虑参数b的Gardner模型对Emax估算的精度更高。

3.3 参数b对Emax的敏感性分析

引入敏感系数用以评价参数b对Emax的影响，不同n值情况下的敏感系数Cn定义为：未忽略参数b时的潜水极限蒸发强度Eb max值与相应n值情况下潜水极限蒸发强度Emax(n)的比值，如公式(7)所示。

(7)

根据公式(7)可导出：

(8)

由公式(8)可知，当H>0.86 cm时，C1.5/C2.0、C2.0/C3.0、C3.0/C4.0均小于1，即Emax(2.0)

对于供试土样(n=2.0)，敏感系数可用公式(9)进行表述，并可对参数b进行敏感性分析。由式(9)可知，∂C2.0/∂b<0，表明C2.0(b)为递减函数，即C2.0随着b值的增加而减小，亦即忽略参数b对Emax的影响随b值增大而逐渐减弱。

(9)

4 讨 论

潜水蒸发实际上是土壤毛细水上升的过程，毛细水上升特性可以用来阐释土壤水分蒸发机理，故将毛细水上升试验和潜水蒸发试验相结合具有理论意义。在地下水浅埋区，地下水中的可溶性盐在蒸发作用下随土壤水向上运移，广泛分布于土壤中甚至在土表聚集，最终导致土壤次生盐渍化。由此看出，明晰潜水蒸发特性对盐碱土富集地区的土壤盐碱化防控具有实践指导意义。

盐分对潜水蒸发的影响是通过改变毛细管力和毛细上升而产生的[15-16]，即土壤中的可溶性盐对土壤孔隙和结构产生了显著影响[17]，进而影响土壤水分运动。在蒸发过程中，析出的盐分吸附在土壤团聚体表面，使土壤孔隙度和透水性发生变化，最终改变了水分运动特性。表2显示，Emax与T呈反比关系，即蒸发强度越小，毛细水上升速率越小，则湿润锋到达顶部所需时间越长，符合实际变化特征。同时表2也表明，与CK处理相比，盐溶液供水处理毛细水上升至土壤表面所需时间较短且极限潜水蒸发强度较大。分析认为，地下水中的可溶性盐在蒸发作用下随土壤水向上运移并滞留在土体中，水分散失过程导致盐分析出结晶。对于矿化度较高的地下水，土壤毛管易被析出的盐分堵塞，增加了毛细管水的上升阻力，对于矿化度较低的地下水，虽然也有盐分析出，但土壤毛细管未被完全堵塞，而是部分沉淀的盐分被吸附在毛细管壁上，使得土壤毛管通道在一定程度上变细，增加了毛细吸力，进而加速了毛细水的上升[18-19]，即为水分蒸发的毛管力驱动机制。另一方面，土壤水溶液中的盐分析出使得土壤孔隙体积减小，导致运输土壤水汽的通道数量减少，从而对土壤水分蒸发产生了一定影响，并且因土壤孔隙体积减小所引起的毛细上升对潜水蒸发的影响大于因土壤通道数量减少对潜水蒸发的影响，最终导致试验中盐溶液供水处理的毛细水上升速率较快且潜水蒸发强度更大。此外，本试验中土柱底部持续供水，故土柱底部土壤盐溶液浓度高于顶部，因此底部土壤土水势较顶部低，加大了水分向下流动的驱动力，因此，随着地下水盐浓度的增加(1～30 g/L)，水分向上流动的驱动力逐渐减弱，导致毛细水上升速率和Emax均表现为随地下水盐浓度的增加而减小。

从理论上讲，基于土壤水动力学理论的Emax计算结果应与其实测值相等，然而本研究发现，无论是否忽略参数b均导致Emax实测值与计算值之间存在差异，分析认为，实际地下水区域的自由水面与土体之间会存在残余空气，而本研究计算Emax时并未考虑水面与土体之间空气对水流运动的影响；另外，实际农田中的层状土较均质土更为常见，不同土层之间往往存在阻力，而对于均质土而言则不考虑该阻力。虽然本试验以均质土体为研究对象，但人工装填土导致相邻土层界面处存在阻力，而基于土壤水运动学理论计算Emax则为理想情况。

本研究仅对K+和Na+影响下的毛管水上升和潜水蒸发特性进行了研究，除此之外，Ca2+和Mg2+也是土壤中常见的盐离子，不同价态会导致土壤胶体的稳定性及其对阳离子的亲和力产生差异[20]，从而使土壤水流运动表现出不同的特征。因此，其他类型盐离子对潜水蒸发特性的影响仍有待探索。在实际农田耕作层中，层状土更为常见且相邻土层土质通常不同，多孔介质物理性质的变化势必对其中水流运动特征造成影响，因此还需开展对层状土壤和不同质地土壤的毛细水上升和潜水蒸发特性的研究。本研究中蒸发试验是在连续光照条件下进行的，没有考虑昼夜交替和降水的影响，昼夜交替将导致上部土壤温度势发生变化，降水将导致上部土壤含水率增加从而减小土壤水势，进而改变土壤水运动特性，在当前研究成果的基础上，还应进一步扩展非稳定蒸发情况下的潜水蒸发特性研究。

5 结 论

(1)与蒸馏水水源供水相比，KCl和NaCl溶液(1～30 g/L)作为供水水源可在一定程度上加快土壤毛细水上升速度进而使Emax值增大；对于K/Na-Cl型盐溶液供水情况，均表现为Emax值随着盐溶液浓度的增加而减小。

(2)无论Gardner模型中的参数b是否被忽略，该模型均可用于估算Emax(相对误差介于1.16%～8.38%)。Gardner模型估算结果与实测值相比，忽略参数b(简化模型)会导致Emax高估，考虑参数b则导致Emax低估；未忽略参数b的Gardner模型具有更高精度，忽略参数b对Emax的影响随b值增大而逐渐减弱。在实际应用中，应根据需要与要求确定是否忽略该模型中的参数b。