THE∂-BOCHNER FORMULAS FOR HOLOMORPHIC MAPPINGS BETWEEN HERMITIAN MANIFOLDS AND THEIR APPLICATIONS∗
Kai TANG(汤凯)
College of Mathematics and Computer Science,Zhejiang Normal University,Jinhua 321004,China
E-mail:kaitang001@zjnu.edu.cn
Abstract In this paper,we derive some∂-Bochner formulas for holomorphic maps between Hermitian manifolds.As applications,we prove some Schwarz lemma type estimates,and some rigidity and degeneracy theorems.For instance,we show that there is no nonconstant holomorphic map from a compact Hermitian manifold with positive(resp.nonnegative)ℓ-second Ricci curvature to a Hermitian manifold with non-positive(resp.negative)real bisectional curvature.These theorems generalize the results[5,6]proved recently by L.Ni on Kähler manifolds to Hermitian manifolds.We also derive an integral inequality for a holomorphic map between Hermitian manifolds.
Key words Schwarz lemmas;Bochner formulas;holomorphic map;Hermitian manifolds;ℓ-second Ricci curvature
1 Introduction
There are many generalizations of the classical Schwarz Lemma on holomorphic maps between unit balls via the work of Ahlfors,Chen-Cheng-Look,Lu,Mok-Yau,Royden,Yau,etc.(see[2,4,8,14]).Here,we recall in particular Yau’s general Schwarz Lemma[14]that a holomorphic map from a complete Kähler manifold of Ricci curvature bounded from below to a Hermitian manifold of holomorphic bisectional curvature bounded from above by a negative constant decreases distances.Recently,there has been signi ficant progress on this topic,which has involed relaxing either the curvature assumptions or the Kählerian condition;see[5,6,9,11,12]and references therein for more details.In particular,Ni[5,6]proved some new estimates interpolating the Schwarz Lemmata of Royden-Yau for holomorphic mappings between Kähler manifolds.These more flexible estimates provide additional information on(algebraic)geometric aspects of compact Kähler manifolds with nonnegative holomorphic sectional curvature,nonnegative Ricℓor positive Sℓ.One wonders if the results of Ni could be extended or modi fied to apply to the Hermitian setting.


We will give speci fic de finitions of these curvatures in the next section.For ℓ=1,the 1-fi rst Ricci curvature and 1-second Ricci curvature are both holomorphic sectional curvature;If ℓ=m=dimM,the m-fi rst Ricci curvature is the(fi rst)Chern Ricci curvature and the m-second Ricci curvature is the second Ricci curavture.For 1≤ℓ≤dimM,they are the same when the metric is Kähler.In an attempt to generalize Wu-Yau’s Theorem([10])to the Hermitian case,Yang and Zheng[13]introduced the concept of real bisectional curvature for Hermitian manifolds.When the metric is Kähler,this curvature is the same as the holomorphic sectional curvature H,and when the metric is not Kähler,the curvature condition is slightly stronger than H,at least algebraically.This condition also appeared in a recent work by Lee and Streets[3],where it is referred to as a“positive(resp.negative)curvature operator”.
The following are the rigidity and degeneracy results:
Theorem 1.5Let f:(Mm,g)→(Nn,h)be a holomorphic map between Hermitian manifolds with M being a compact.Let m≤n and ℓ≤m.Then,

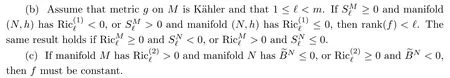
In particular,from the proof of theorem 1.5(c),we easily get the following result:
Corollary 1.6There is no non-constant holomorphic map from a compact Hermitian manifold with positive(resp.non-negative)holomorphic sectional curvature to a Hermitian manifold with non-positive(resp.negative)holomorphic sectional curvature.
Note that the above Corollary 1.6 is also proved independently by Yang in[11,12]using a different method.
As an application of Theorem 1.1,we will also give an integral inequality for non-degenerate holomorphic maps between two Hermitian manifolds without assuming any curvature condition.More precisely,we shall prove the following:
Theorem 1.7Let(Mm,g)and(Nn,h)be two Hermitian manifolds and let M be compact.Assume that dimM=m≤n=dimN.Then there exists a smooth real function ψ on M such that for any non-degenerate holomorphic map f:M→N,it holds that
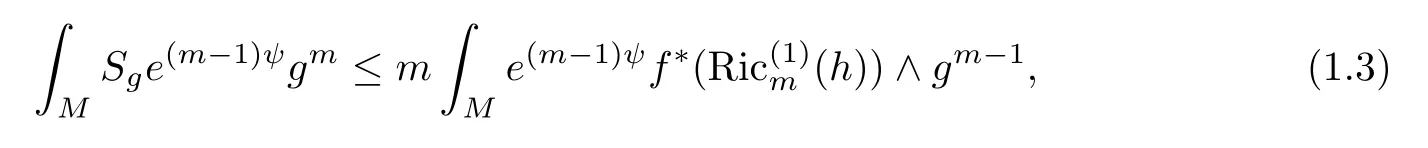
where Sgis the Chern scalar curvature of g andis the m-fi rst Ricci curvature of h.
Remark 1.8The above Theorem 1.7 recovers Theorem 1.2 in[15],which is proved by Zhang when dimM=dimN.The above result can be applied to prove degeneracy theorems for holomorphic maps without assuming any pointwise curvature signs for both the domain and the target manifolds.
2 Preliminaries
2.1 Curvatures in complex geometry
Let(M,g)be a Hermitian manifold of dimension dimCM=m,where ω=ωgis the metric form of a Hermitian metric g.If ω is closed,that is,if dω=0,we call g a Kähler metric.In local holomorphic chart(z1,···,zm),we write
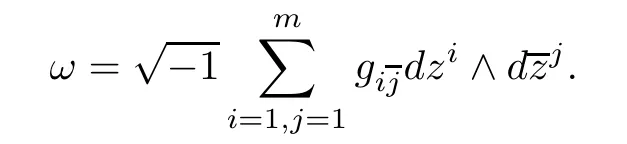
Recall that the curvature tensor R=of the Chern connection is given by
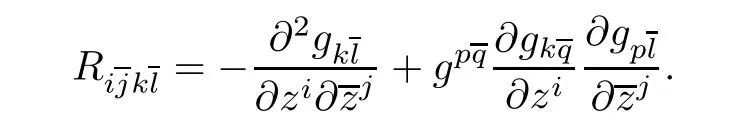
Then the(fi rst)Chern Ricci curvature Ric(ωg)=trgR∈Γ(M,∧1,1T′∗M)has components
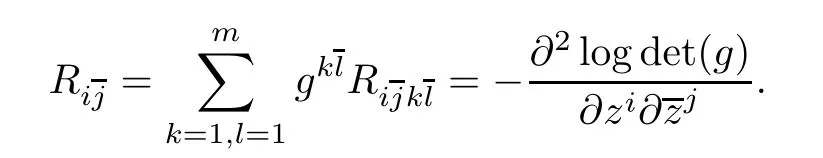
The second Chern Ricci curvature Ric(2)(ωg)=trωgR∈Γ(M,End(T′M))has components
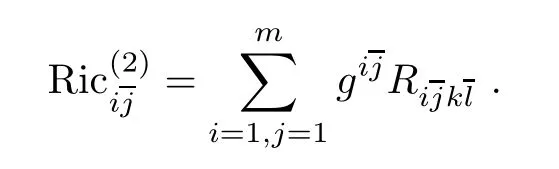
Note that Ric(ωg)and Ric(2)(ωg)are the same when ωgis a Khler metric.The Chern scalar curvature Sωis given by
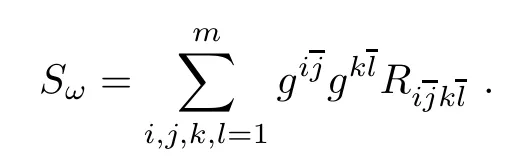
The holomorphic bisectional curvature B(X,Y)for X,Y inM at p∈M is given by
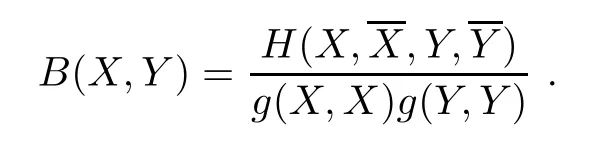
The holomorphic sectional curvature H(X)is denoted by

Let us recall the concept of real bisectional curvature introduced in[13].Let(Mm,g)be a Hermitian manifold.Denote by R the curvature tensor of the Chern connection.For p∈M,let e={e1,···,em}be a unitary tangent frame at p,and let a={a1,···,am}be non-negative constants with|a|2=+···+>0.De fine the real bisectional curvature of g by
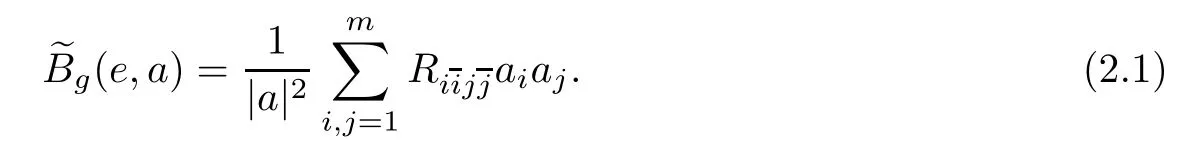
We will say that a Hermitian manifold(Mm,g)has positive real bisectional curvature,denoted by>0,if,for any p∈M and any unitary frame e at p,and any nonnegative constant a={a1,···,am},it holds that(e,a)>0.
Recall that the holomorphic sectional curvature in the direction υ is de fined by H(υ)=If we take e so that e1is parallel to υ,and take a1=1,a2=···=am=0,thenbecomes H(υ).Thus,>0(≥0,<0,or≤0)implies that H>0(≥0,<0,or≤0).For a more detailed discussion of this,we refer readers to[13].
2.2 Gauduchon metric
Let Mmbe a compact Hermitian manifold.A Hermitian metric ω is called Gauduchon if
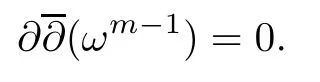
For a Gauduchon metric ω and a smooth function u on M,we easily get
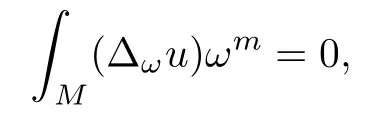
where∆ωu is the complex Laplacian de fined by∆ωu=A classical result of Gauduchon[1]states that,for any Hermitian metric ω,there is a ψ∈C∞(M,R)(unique up to scaling)such that eψω is Gauduchon.
2.3 Non-degenerate holomorphic maps
Let f:Mm→Nnbe a holomorphic map between two Hermitian manifolds(m≤n).If dim(f(M))=m,then we say that f is non-degenerate.If dim(f(M)) In this section,we will give the proof of Theorems 1.1 and 1.2.The calculation is more complicated in the Hermitian case than in the Khler case. The last two lines only hold at point p. Similarly, Taking the second derivative and evaluating at p,we have Putting all of the above together,we can get the formula(1.1). where ΘEis the curvature of the vector bundle E with respect to the induced metric,since More precisely,we can assume that Hence,at the point p assumed in the theorem condition,we have Putting all the above together,we can get the formula(1.2). Proposition 4.1([6],Proposition 2.1) For any 1≤ℓ≤m,the following holds: Proposition 4.2([6],Proposition 2.2) For any 1≤ℓ≤m,the following holds: Proof of Theorem 1.4To prove part(a),let D==Wm.Since M is compact,D attains its maximum at some point p.We assume that at p,D is not equal to zero.Then in a neighborhood of p,D0.The maximum principle then implies that at p,with respect to the coordinates speci fied in Theorem 1.1, The proof of part(c)is similar.We assume that σℓattains a maximum at p.We also assume that the coordinates at p and f(p)satisfy the conditions of Theorem 1.2,so Uℓ(x)≤σℓ(x)≤σℓ(p)=Uℓ(p)for x in the small neighborhood of p.Thus,at p, Combining Theorems 1.1,1.2 and 1.4,we can now easily prove Theorem 1.5. Proof of Theorem 1.5If f is not degenerate,then D==Wmhas a nonzero maximum somewhere at p.By using the coordinates around p and f(p),speci fied as in Theorem 1.4,at p,we have that This leads to a contradiction under the assumption that either SM≥0 and manifold(N,h)has<0,or that SM>0 and≤0.For the second part of(a),we introduce the operator The above also induces a contradiction under either RicM≥0 and<0,or RicM>0 and≤0. The proof of(b)is similar to that of(a).It is worth noting that in the second part of(b),we need to introduce the operator For(c),if f is not constant,σℓwill attain a maximum somewhere,say at p and σℓ(p)>0.By using the coordinates around p and f(p),speci fied as in Theorem 1.4,at p,we have that In this section we prove Theorem 1.7.The proof does not use any maximum principle argument,since the curvatures and target spaces may not be signed in a pointwise sense.This method was essentially derived by Zhang in[15]. Proof of Theorem 1.7Because f is a non-degenerate holomorphic map,we assume that p∈M with D(p)=(p)>0.We also assume that the coordinates at p and f(p)satisfy the conditions of Theorem 1.1.Let∊be an arbitrary positive constant.By the formula(1.1),at p,we have Here we note that the above inequality is independent of the choice of coordinates. Set V={x∈M|D=0 at x},which is a proper subvariety(may be empty)of M.Then,the above inequality(5.1)holds on MV,and by continuity we know that it holds on the whole of M. Now,we can easily use the same arguments as to those in Theorem 1.1 in[15]to complete the proof. AcknowledgementsThe author is grateful to Professor Fangyang Zheng for constant encouragement and support.He wishes to express his gratitude to Professor Lei Ni for many useful discussions on[5,6].
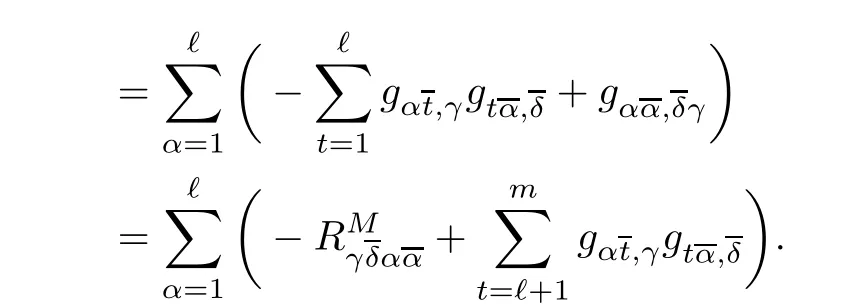
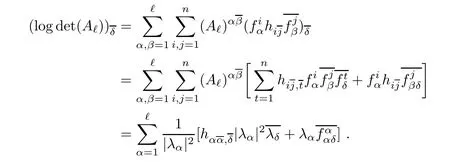
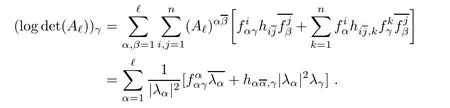
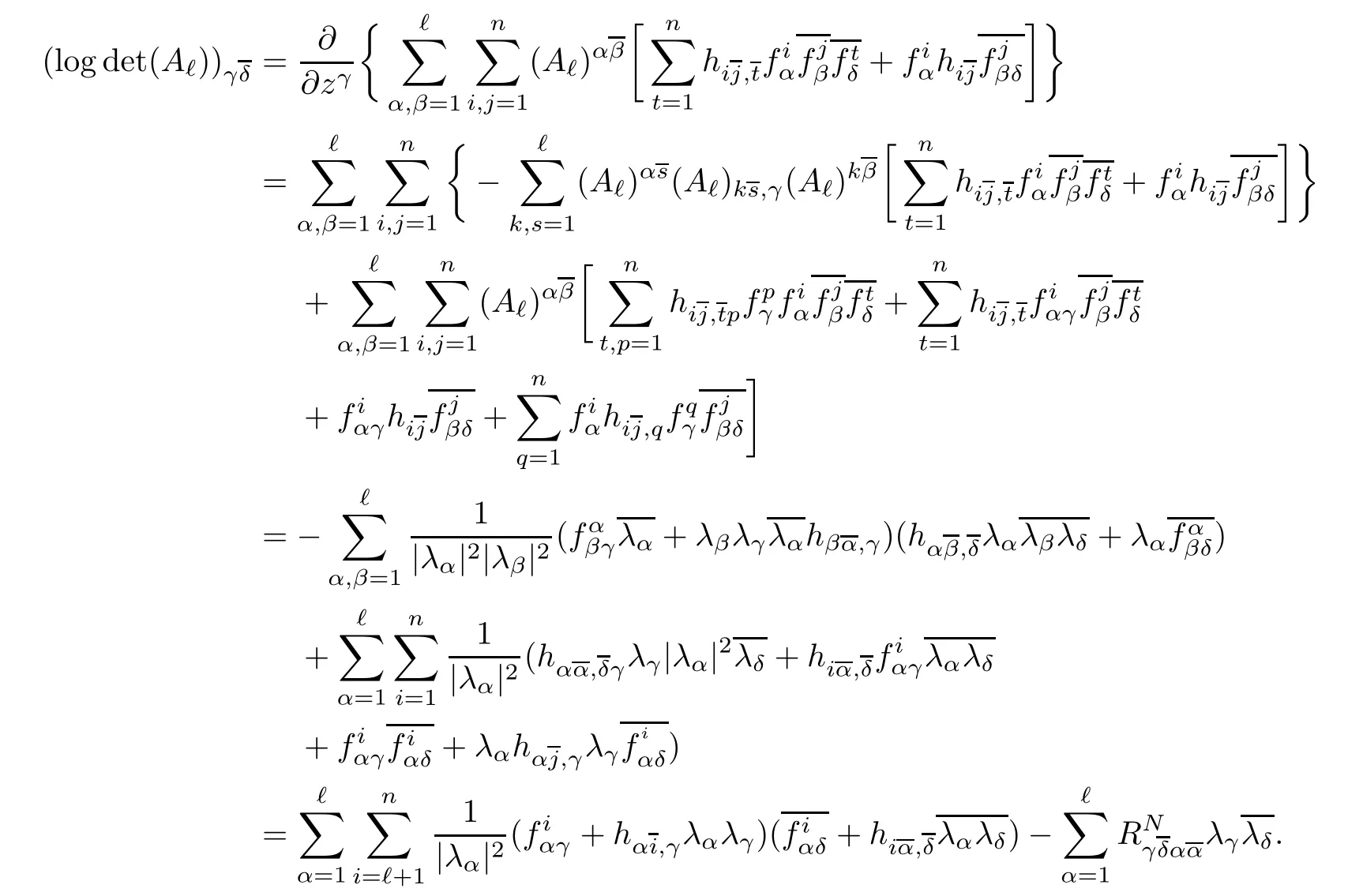
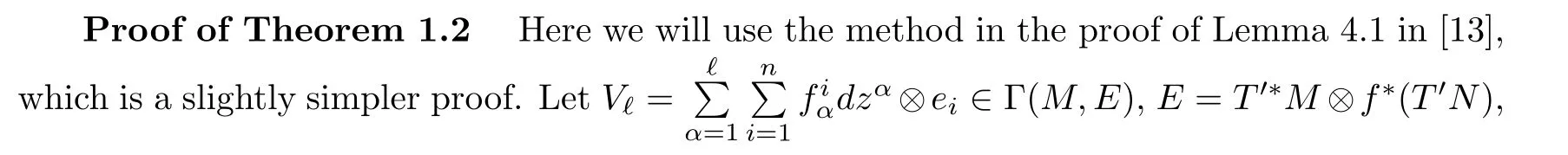

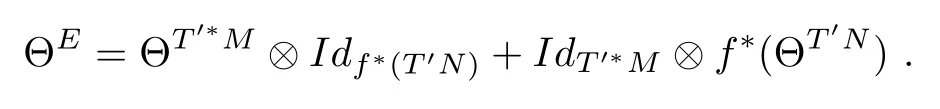
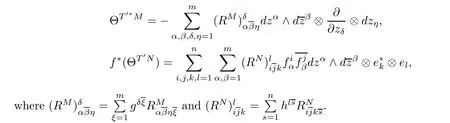
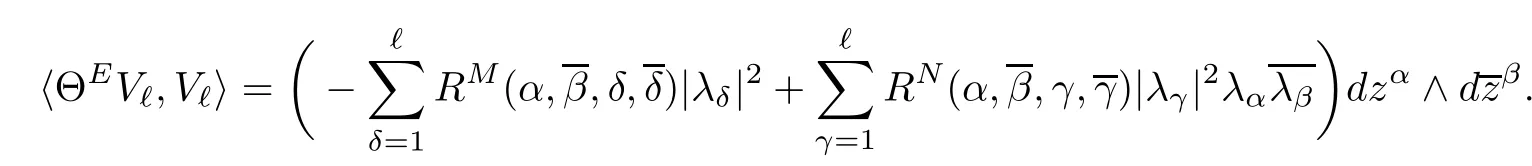
4 Applications

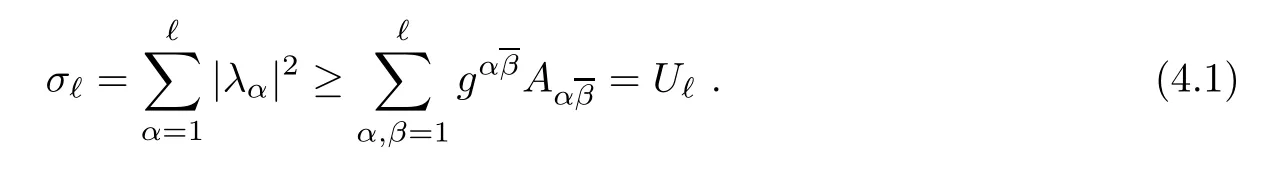

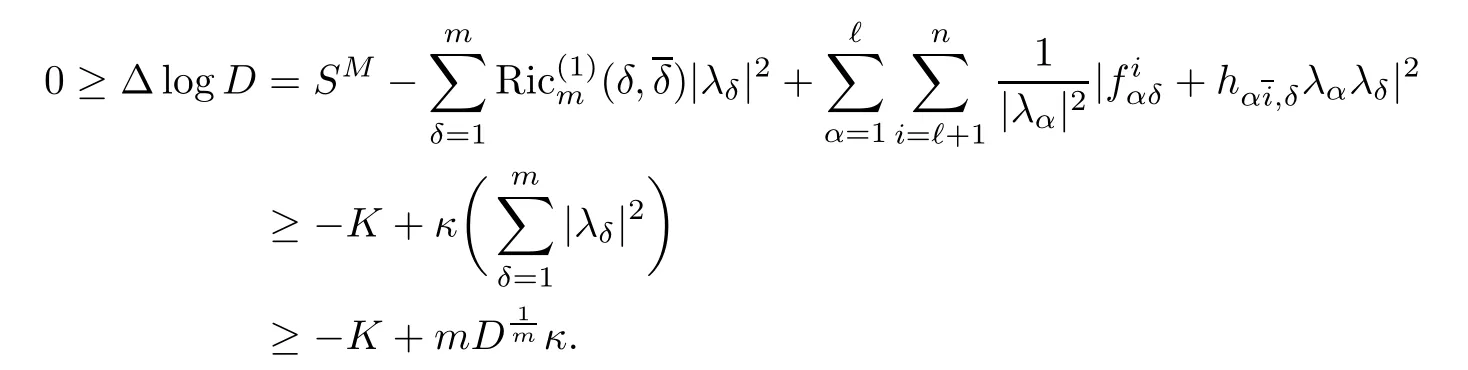

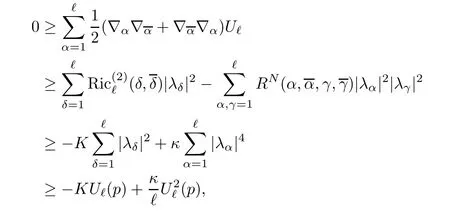
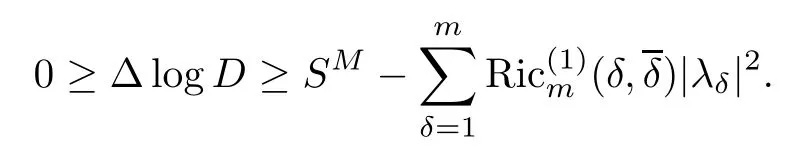
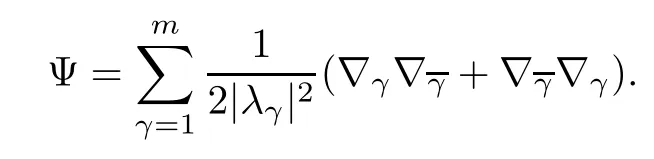
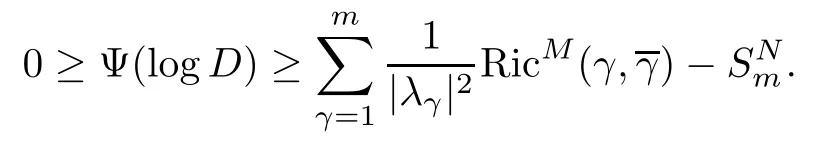
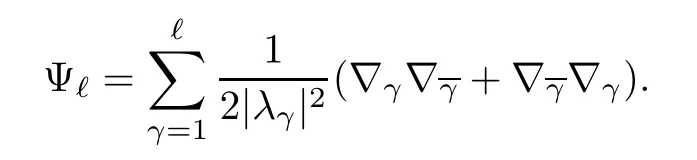
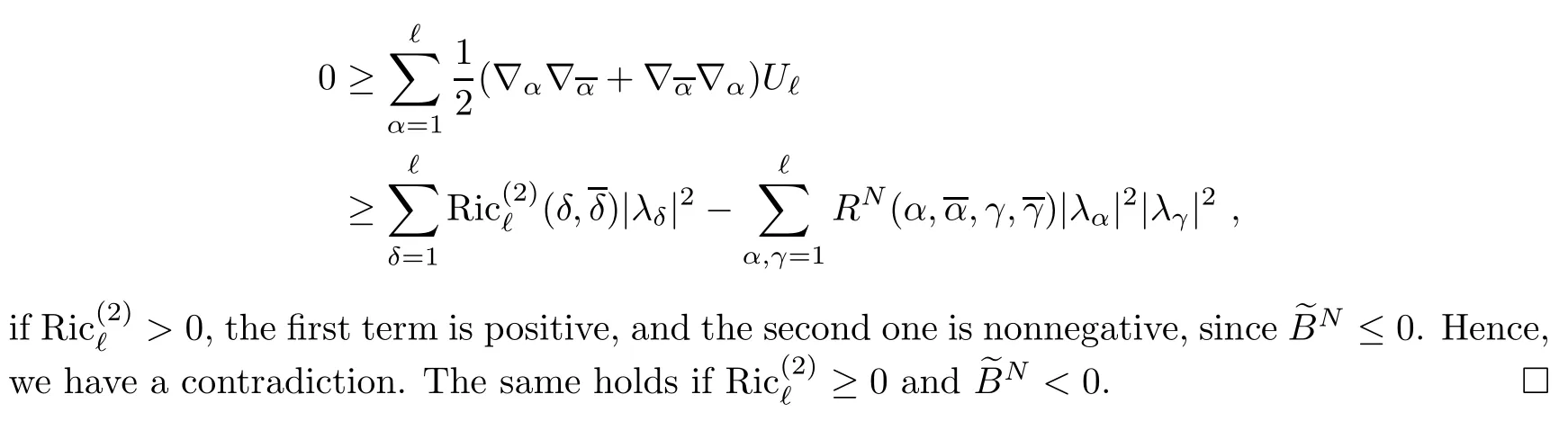
5 An Integral Inequality for Non-degenerate Holomorphic Maps
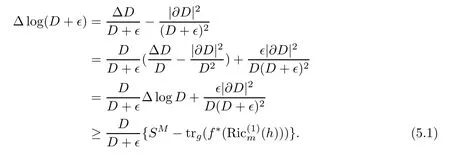
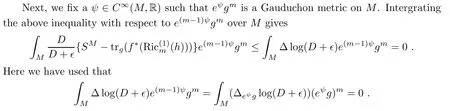
 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
- Acta Mathematica Scientia(English Series)的其它文章
- RIGIDITY RESULTS FOR SELF-SHRINKING SURFACES IN R4∗
- GLOBAL STRONG SOLUTION AND EXPONENTIAL DECAY OF 3D NONHOMOGENEOUS ASYMMETRIC FLUID EQUATIONS WITH VACUUM∗
- CONTINUOUS TIME MIXED STATE BRANCHING PROCESSES AND STOCHASTIC EQUATIONS∗
- SOME OSCILLATION CRITERIA FOR A CLASS OF HIGHER ORDER NONLINEAR DYNAMIC EQUATIONS WITH A DELAY ARGUMENT ON TIME SCALES∗
- COARSE ISOMETRIES BETWEEN FINITE DIMENSIONAL BANACH SPACES∗
- ZERO KINEMATIC VISCOSITY-MAGNETIC DIFFUSION LIMIT OF THE INCOMPRESSIBLE VISCOUS MAGNETOHYDRODYNAMIC EQUATIONS WITH NAVIER BOUNDARY CONDITIONS∗
