THE NONEMPTINESS AND COMPACTNESS OF MILD SOLUTION SETS FOR RIEMANN-LIOUVILLE FRACTIONAL DELAY DIFFERENTIAL VARIATIONAL INEQUALITIES∗

Yirong JIANG(蒋宜蓉) Zhouchao WEI(魏周超) Jingping LU(卢景苹)†

1.College of Science,Guilin University of Technology,Guilin 541004,China

2.School of Mathematics and Physics,China University of Geosciences(Wuhan),Wuhan 430074,China

E-mail:jiangyirong996@126.com;weizhouchao@163.com;lujingbaby520@163.com

Abstract This paper investigates the nonemptiness and compactness of the mild solution set for a class of Riemann-Liouville fractional delay differential variational inequalities,which are formulated by a Riemann-Liouville fractional delay evolution equation and a variational inequality.Our approach is based on the resolvent technique and a generalization of strongly continuous semigroups combined with Schauder’s fixed point theorem.

Key words differential variational inequality;Riemann-Liouville fractional delay evolution equation;resolvent;Schauder’s fixed point theorem

1 Introduction

Pang and Stewart in[14]introduced and investigated the differential variational inequality(DVI).They pointed out that the DVI is a useful mathematical tool for the modeling of systems that simultaneously involve dynamics and constraints in the form of inequalities arising in several applied areas,such as electrical circuits with ideal diodes,Coulomb friction problems for contacting bodies,economical dynamics,dynamic traffic networks and so on.Since then,more and more scholars have paid attention to the study of DVI.For details and examples,we refer the reader to the monographs by Stewart[15],and the series of papers[8,10,12]and the references cited therein.Recently,Ke-Loi-Obukhovskii[5],Ke and Tuan[6],Loi-Ke-Obukhovskii[11],Zeng-Liu-Mig´orski[18],Mig´orski and Zeng[13],Jiang-Huang-Wei[4],and Weng-Li-Huang[16]studied the qualitative properties and the behavior of mild solutions for Caputo fractional differential variational inequalities(FDVIs).However,to the best of our knowledge,there have been no results about the nonemptiness and compactness of the mild solution set for a class of Riemann-Liouville fractional delay differential variational inequalities(RL-FDDVIs).

In this paper,we consider the fractional delay differential variational inequality

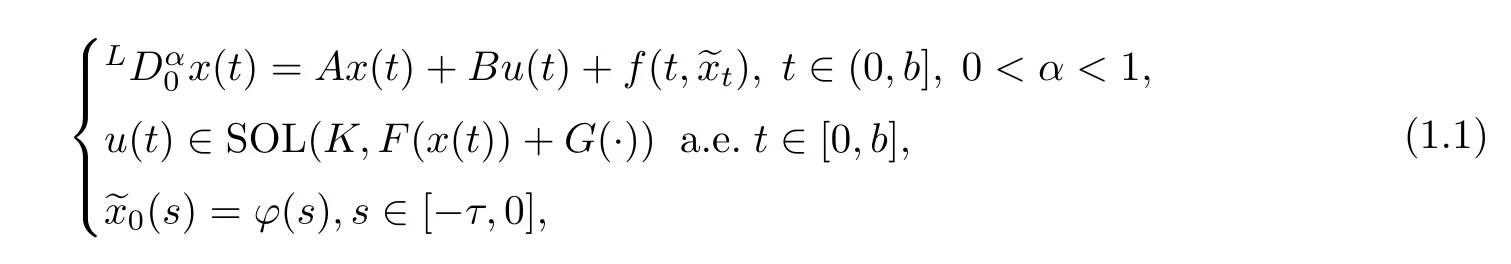
whereLstands for Riemann-Liouville fractional time derivatives of order α,A:D(A)⊆X→X is an operator generating α-order fractional resolvent{Qα(t)}t>0on X,X is a Banach space equipped with the norm‖·‖,ϕ is continuous on[−τ,0],(t)=Γ(α)t1−αx(t)for t∈(0,b],

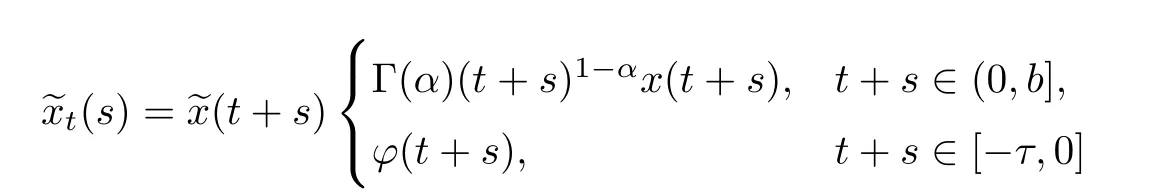
for t∈(0,b]and s∈[−τ,0],K is a closed convex subset of a separable Hilbert space Y with the norm‖·‖Y,and the notation SOL(K,F(x(t))+G(·))denotes the solution set of the following variational inequality(VI):fi nd u:[0,b]→K such that

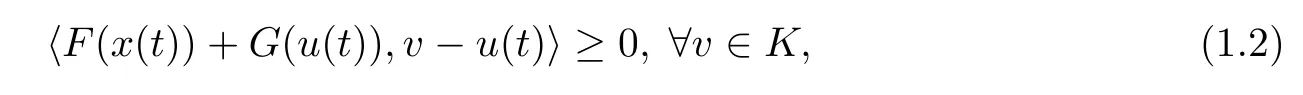
where the notation〈·,·〉denotes the canonical pairing between Y and its dual Y∗,and B,f,F,G are given but will be speci fied later.

The novelties of this paper are threefold.The first novelty is that all of the aforementioned works were considered under the Lipschitz assumption of the nonlinear term f,while we remove the Lipschitz assumption of the nonlinear term f without imposing any additional conditions.In addition,in contrast to fractional evolution equations(inclusions)with the Cauchy initial and delay conditions considered in[5,6,11,13,18],we consider the Riemann-Liouville fractional evolution equations with the Riemann-Liouville integral delay initial condition.However,as pointed out by Heymans and Podlubny[3],and Zhu-Fan-Li[19],the Riemann-Liouville initial and delay conditions are more appropriate than physically interpretable initial conditions.This represents the second novelty of the present work.It is well-known that the solutions of Riemann-Liouville fractional systems admit singularity at zero,while the aforementioned works[4–6,11,13,18]consider fractional evolution systems without singularity at zero.Thus,the third novelty of the paper is that methods and techniques of aforementioned works are not applicable here;we use the resolvent technique,a generalization of strongly continuous semigroups and Schauder’s fixed point theory to solve RL-FDDVIs(1.1).

The plan of this paper is as follows:Section 2 gives some preliminaries,and Section 3 is dedicated to the nonemptiness and compactness of the mild solution set for RL-FDDVIs.

2 Preliminaries

Let L(X,Y)be the space of all bounded linear operators from X to Y,and let L(X)denote L(X,X).For I⊂R,p>,let Lp(I,X)be the Banach space of all Bochner integrable functions from I into X with the norm

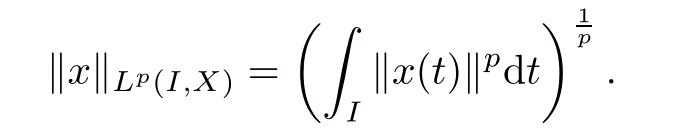
The symbol C([d,e];X)denotes the space of all X-valued functions which are continuous and normed by

We now recall regarding some notions of the fractional calculus theory,as well as the concept and some properties of the resolvent.

De finition 2.1(see[7]) Let α∈(0,1)and x∈L1([0,∞);X).The Riemann-Liouville fractional integral of order α is de fined by

where∗stands for the convolution

For x∈C([0,∞);X),the Riemann-Liouville fractional derivative of order α is de fined as

De finition 2.2(see[9]) For α∈(0,1),a function Qα:(0,∞)→L(X)is said to be an α-order fractional resolvent if it satis fies the following assumptions:

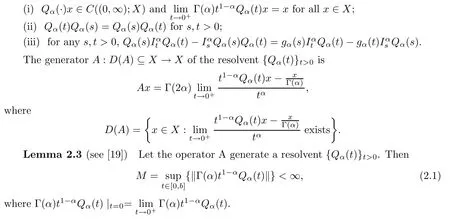
Lemma 2.4(see[9]) Assume that{Qα(t)}t>0is a resolvent with generator A.Then,

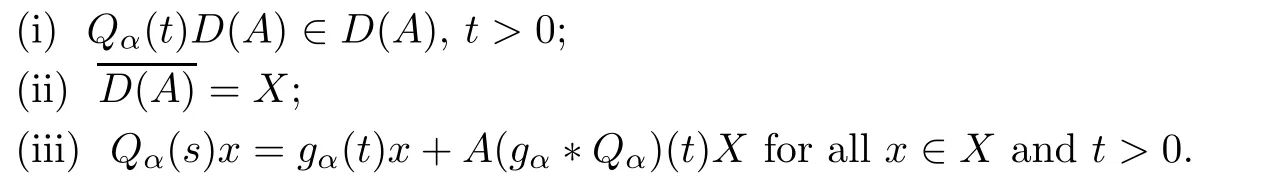
3 Nonemptiness and Compactness of Mild Solution Sets

In this section,we study problem RL-FDDVIs under the following assumptions:

(HA){t1−αQα(t)}t>0is compact and there exists a constant C>0 to ensure that

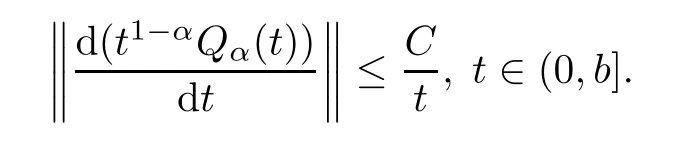
(HB)B:L([0,b];Y)→L([0,b];X)is a bounded linear operator.

(Hf)The nonlinear map f:[0,b]×C([−τ,0];X)→X satis fies the condtions that

(f1)v→f(t;v)is continuous for almost every t∈[0,b];

(f2)t→f(t;v)is measurable for each v∈C([−τ,0];X);

(f3)for all v∈C([−τ,0];X)and almost every t∈[0,b],

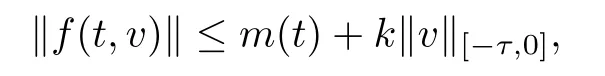
(HF)The function F:X→Y∗is Lipschitz continuous with constant LF,i.e.,

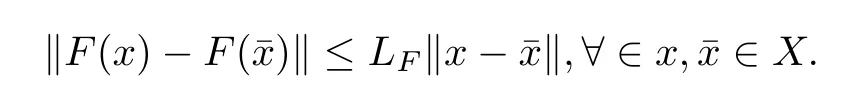
(HG)The function G:Y→Y∗is de fined by

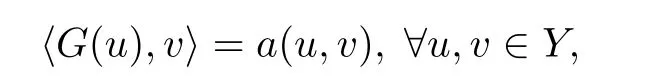
where a:Y×Y→R is a bilinear continuous function on Y×Y such that

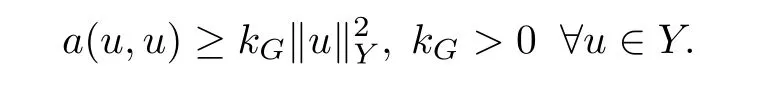
Remark 3.1The condition(HA)comes from the practical problems.Moreover,by Lemma 3.8 of[2],if{t1−αQα(t)}t>0is a compact and analytic operator family of analyticity type(ω0,θ0),then(HA)is automatically satis fied.

Lemma 3.2(see[19]) Let condition(HA)hold and let p>.Then,

(i)Qα∗g∈C([0,b];X),where g∈Lp([0,b];X);

(ii)the operator Θ:Lp([0,b];X)→C1−α([0,b];X)de fined by(Θg)(·)=(Qα∗g)(t)is compact.

For z∈Y∗,we denote

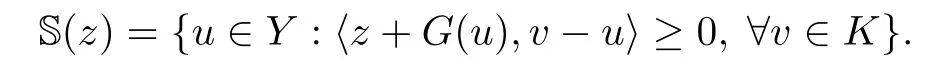
Lemma 3.3(see[6]) Let condition(HG)holds.Then,for each z∈Y∗,the solution set S(z)is a singleton.Moreover,the map z→S(z)is Lipschitz continuous from Y∗to Y with constant kG,i.e.,

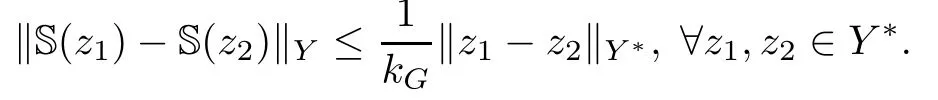
We have a variational inequality that is the original form of(1.2),i.e.,for a given∈X,if consists in finding∈K such that

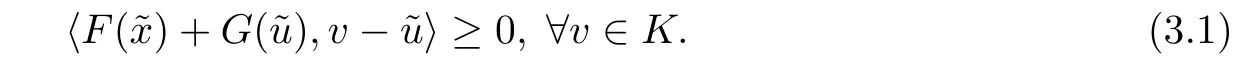
Lemma 3.4(see[6]) Let the conditions(HF)and(HG)hold.Then,for each∈X,(3.1)has a unique solution∈Y.Moreover,the solution map

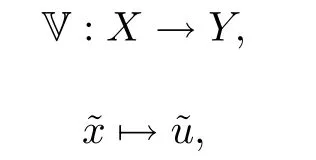
is Lipschitz continuous.More precisely,

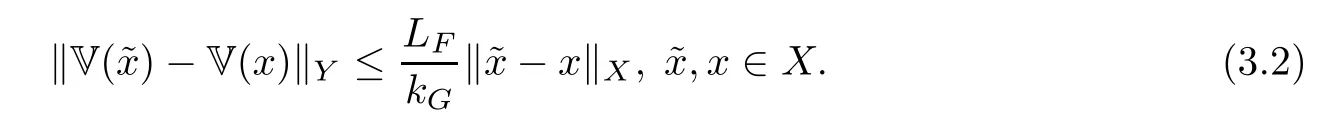
In order to solve RL-FDDVI(1.1),we reformulate it as an equivalent fractional evolution equation.To this end,we consider the map

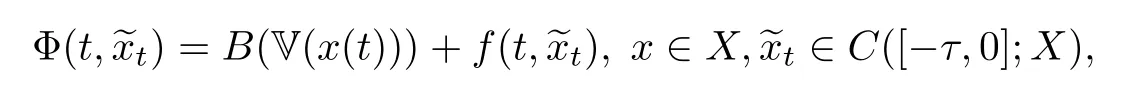
and the fractional evolution equation

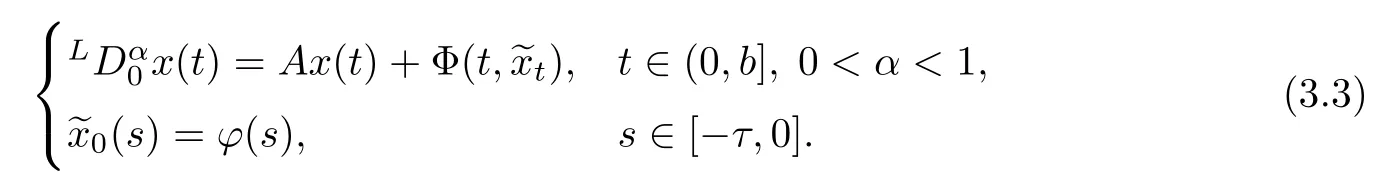
To formulate the de finition of mild solutions to(3.3)by the resolvent technique,for convenience,we now consider the fractional evolution equation

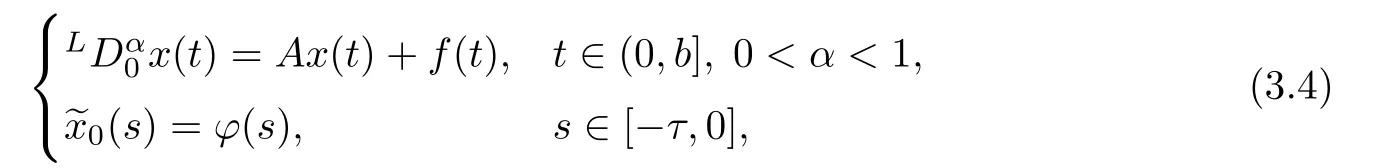
where f∈Lp([0,b];X),ϕ is continuous on[−τ,0].

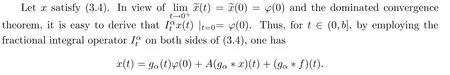
Employing(iii)of Lemma 2.4,it follows that

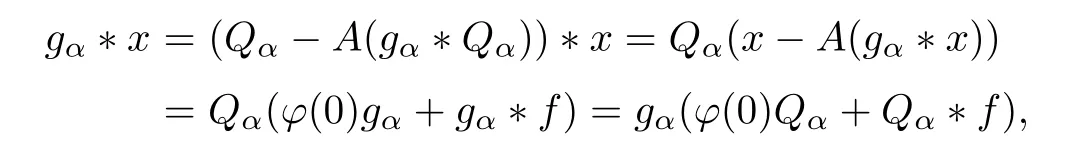
which implies that

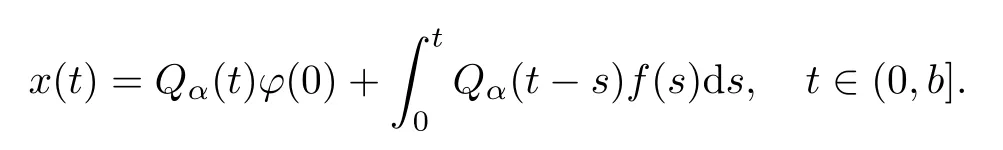
According to the aforementioned setting,(3.3),Pang and Stewart[14],and Zhu-Fan-Li[19],we give the de finition of the solutions for problem(1.1)in the mild sense.

De finition 3.5A pair(x,u)with∈C([−τ,b];X)and u:[0,b]→K integrable is called a mild solution of RL-FDDVI(1.1)(also(3.3))if x|(0,b]∈C1−α([0,b];X),

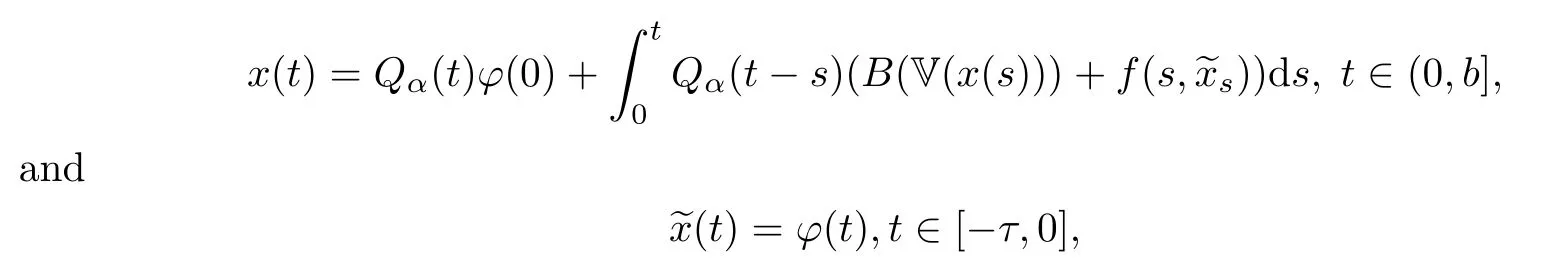
where u(t)=B(V(x(t)))∈SOL(K,F(x(t))+G(·))a.e.t∈[0,b].

Remark 3.6For x∈C1−α([0,b];X),let

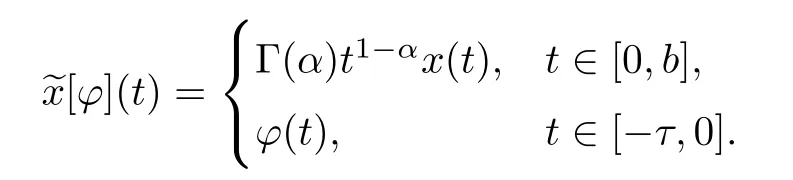
Then,based on De finitions 2.2,3.5 and Lemma 3.2,[ϕ]∈C([−τ,b];X)is a mild solution of RL-FDDVIs related to u if and only if x∈C1−α([0,b];X)satis fies

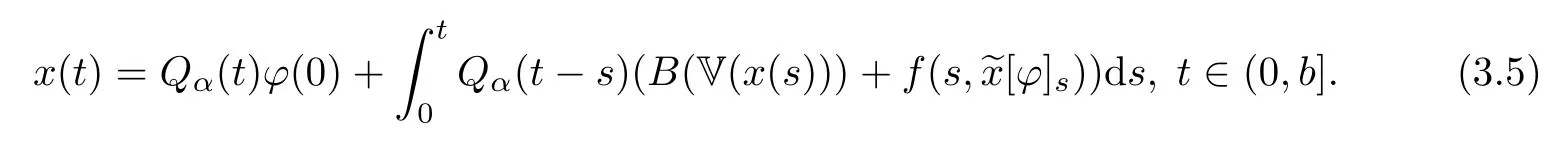
For simplicity,we put that W(u)={x∈C1−α([0,b];X):x satis fies(3.5)}and abbreviate the notation[ϕ]to.

Theorem 3.7If hypotheses(HA),(HB),(Hf),(HF)and(HG)hold,then W(u)is nonempty and compact.

ProofBy the de finition of mild solutions for RL-FDDVIs(see De finition 3.5)and Lemma 3.2,a map Ψ:C1−α([0,b];X)→C1−α([0,b];X)is de fined by

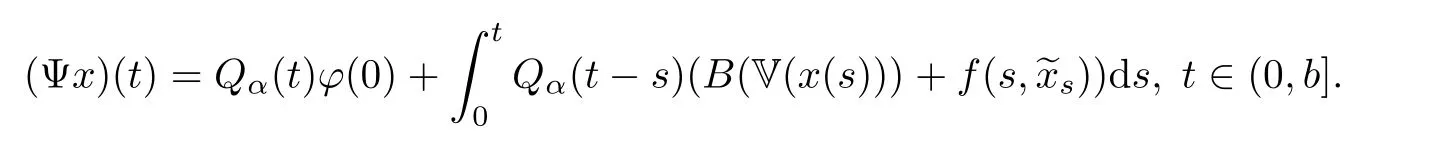
Since x∈W(u)is equivalent to x∈Fix(Ψ),our problem is reduced to checking that Fix(Ψ)is nonempty and compact.Put

where

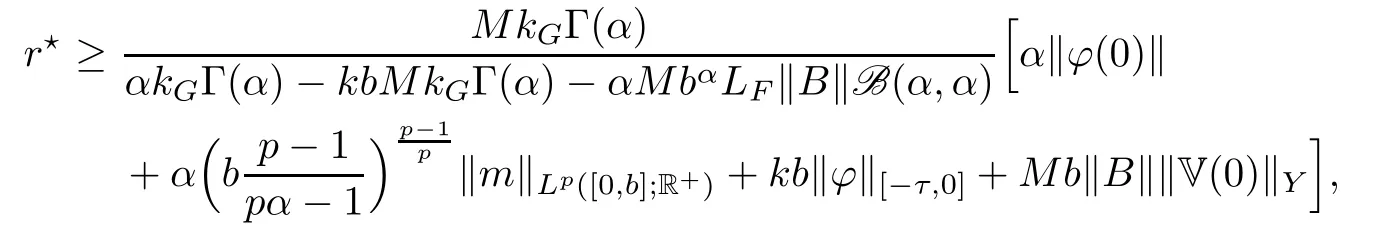
whereB(α,α)is the beta function.We divide our proof into four steps.

Step 1We shall prove that Ψ(Br⋆)⊆Br⋆.

Let x∈S(u).Then ρ∈[0,t],t∈(0,b],so one has

Let x∈Br⋆.Then,for s∈[0,t],t∈(0,b],by(3.2),one has

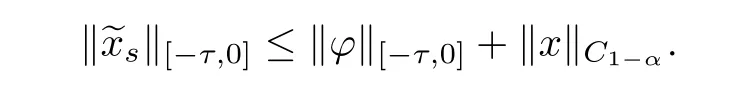
In addition,we give the growth of Φ(see(3.3)),and by conditions(f3),(HB)and(3.2),we get

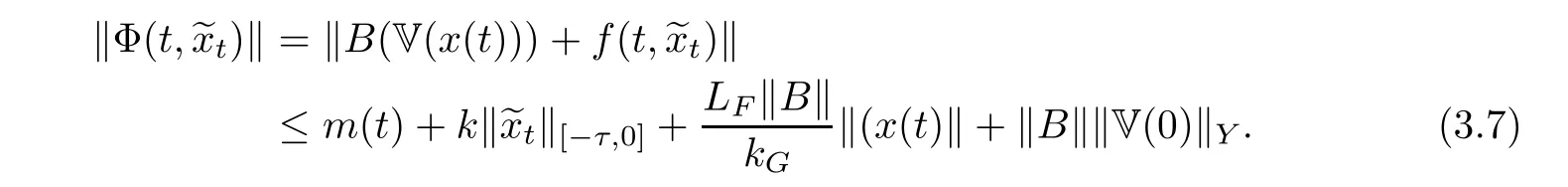
Thus,for t∈(0,b],from(3.6),(3.7),Lemma 2.3,and H¨older’s inequality,we obtain that

Consequently,for t∈(0,b],by mean of H¨older’s inequality and the dominated convergence theorem,we can prove that

4 An Example

We consider the following problem:fi nd x:[0,1]×(0,1)→R and u:[0,1]×(0,1)→R satisfying

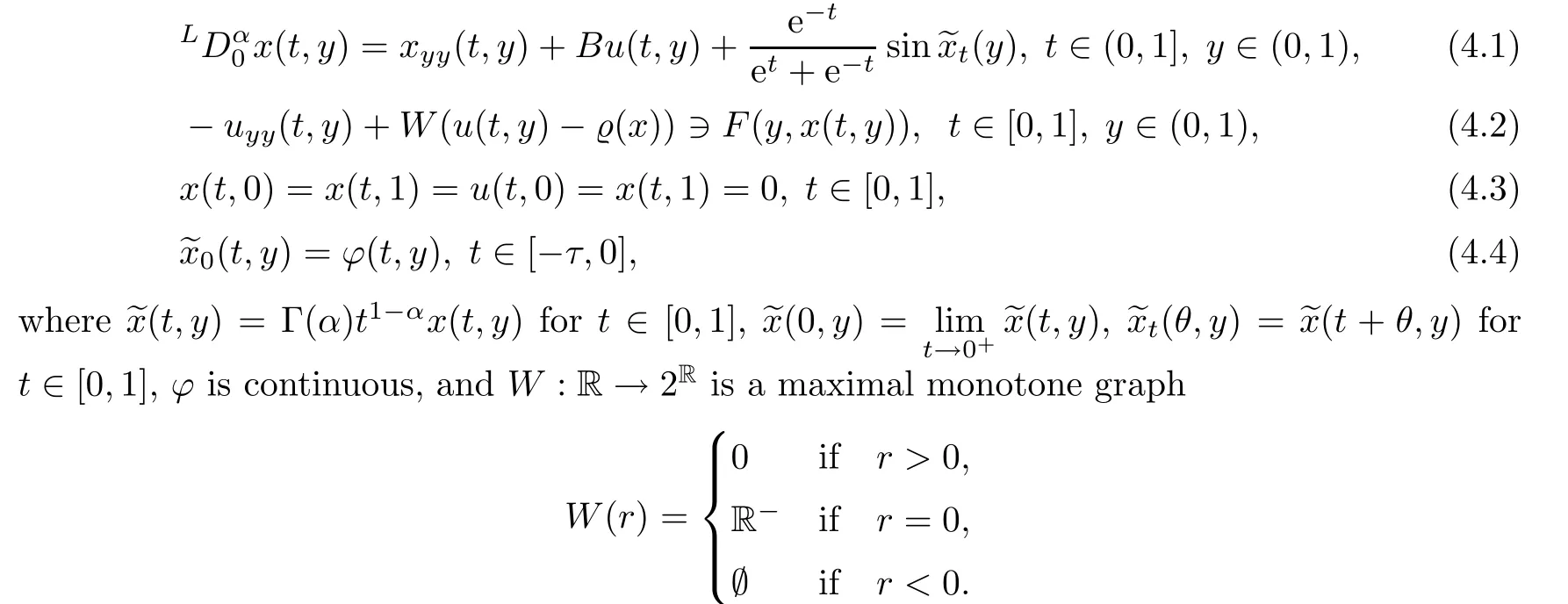
Let X=Y=L2(0,1),we de fine the operator A:D(A)⊂L2(0,1)→L2(0,1)as follows:

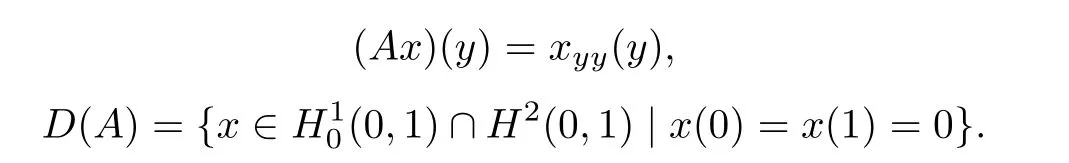
It is well known from the application of[6]and example 5.1 of[19]that A satisfes hypothesis(HA)on the space X=L2(0,1).Moreover,the semigroup T(t)=eAtgenerated by A is compact and exponentially stable,i.e.,

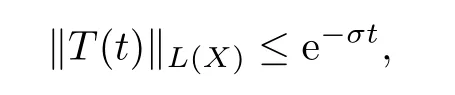
Then f is bounded.Therefore,we can take k=0 in condition(Hf).

In addition,let B:L2([0,1];Y)→L2([0,1];X)be an operator de fined in(5.2)of[19].From example 5.1 of[19],we know that the operator B satis fies assumption(HB).

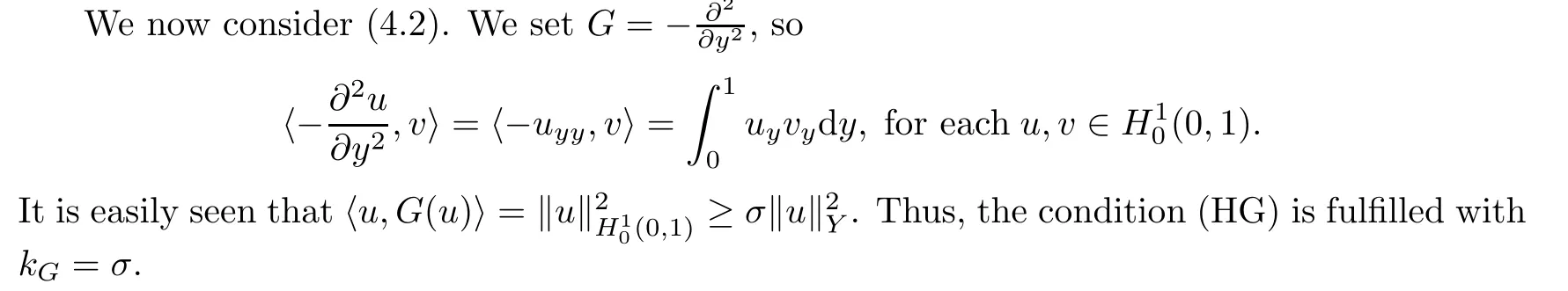
Regarding nonlinear function F appearing in(4.2),we assume that F is Carath´eodory function de fined on(0,1)×R such that

where LF∈L2(0,1).We consider the following abstract form of F:

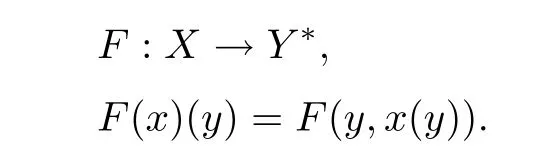
It follows that

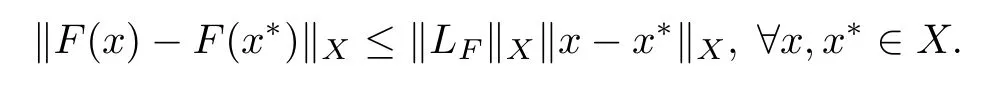
By the same arguments as in[1,Proposition 2.11],(4.2)can be written as

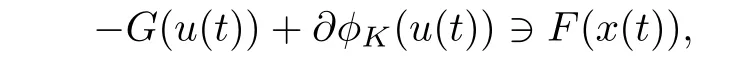
where

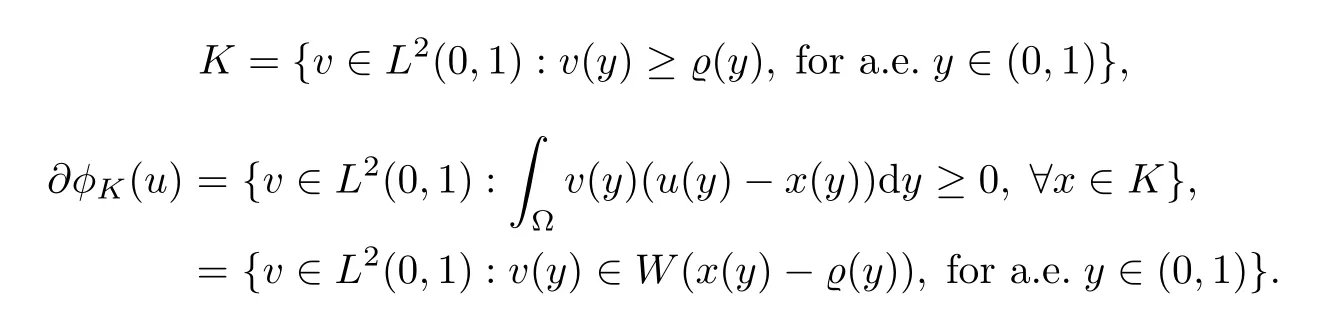
Therefore,problem(4.1)–(4.4)can be written as the abstract form of RL-FDDVI(1.1).