ON THE(p,q)-MELLIN TRANSFORM AND ITS APPLICATIONS∗
Pankaj JAIN Chandrani BASU Vivek PANWAR
Department of Mathematics,South Asian University Akbar Bhawan,Chanakya Puri,New Delhi-110021,India
E-mail:pankaj.jain@sau.ac.in,pankajkrjain@hotmail.com;chandrani.basu@gmail.com;vivek.pan1992@gmail.com
Abstract In this paper,we introduce and study a(p,q)-Mellin transform and its corresponding convolution and inversion.In terms of applications of the(p,q)-Mellin transform,we solve some integral equations.Moreover,a(p,q)-analogue of the Titchmarsh theorem is also derived.
Key words q-Mellin transform;(p,q)-Mellin transform;inversion formula;convolution;integral equation
1 Introduction
Integral transforms play an important role in solving many differential and integral equations.Riemann[1] first recognized the Mellin transform in 1876 in his famous memoir on prime numbers.The explicit formulation was given by Cohen in 1894,and almost simultaneously,Mellin[2]gave an elaborate discussion of it,along with its inversion formula.
The Mellin transform and its inversion formula can be derived from the complex Fourier transform.More precisely,the Mellin transform of a suitable function f over(0,∞)is given by
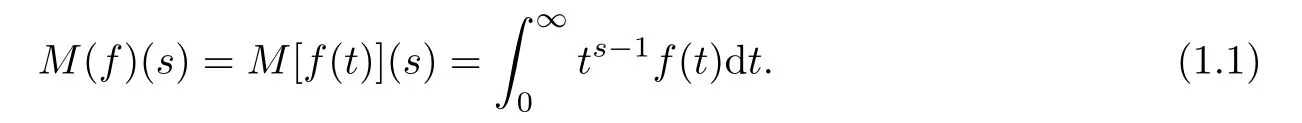
The integral(1.1)is well de fined in a(possibly empty)maximal open vertical strip〈α,β〉,which is called a fundamental strip.The inversion formula for the Mellin transform is given by the following line integral:
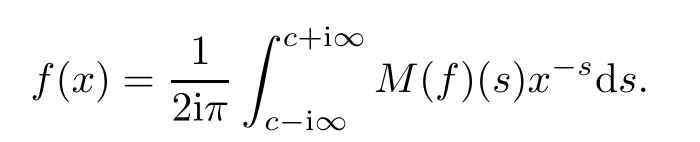
The Mellin convolution product of two suitable functions f and g is de fined by
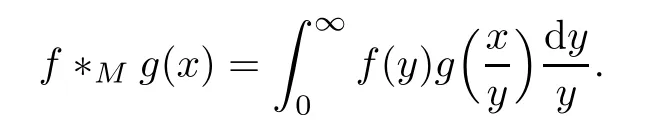
The Mellin transform and the corresponding convolution satisfy the following relations:
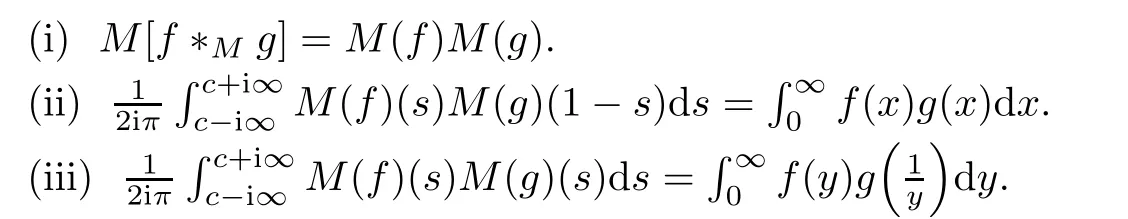
The development of quantum calculus,also called q-calculus or‘limitless’calculus,was started in the 1740s by Euler,and its progress continued under C.F.Gauss,who in 1812 invented the hypergeometric series and its contiguity relations[3].The study of quantum calculus or q-calculus has accelerated in the past two decades.It has been used in several fields in mathematical,physical and engineering sciences.Fitouhi et al.[4]introduced the concept of a q-Mellin transform and studied its applications in solving some integral equations.Later on,Brahim et al.[5]applied the q-Mellin transform to solving partial differential equations.The finite Mellin transform[6]and two dimensional Mellin transforms[7]have also been studied in the framework of quantum calculus.
The notion of q-calculus has further been generalized to post-quantum calculus,or(p,q)-calculus[8–10].In the recent past,(p,q)-calculus has been applied in several areas,such as approximation theory,computer aided geometric design,inequalities etc..For the relevant literature on these applications,one may refer to[11–18].The Laplace transform in the(p,q)-framework[9]has also been studied.
In this paper,we introduce and study some properties of the(p,q)-Mellin transform,as well as its inversion and convolution.Also,we appy the(p,q)-Mellin transform to solving some integral equations.Moreover,the Titchmarsh theorem[19]is proved in the framework of(p,q)-calculus.
2 Preliminaries
2.1 q-Calculus
Throughout this paper we shall take q∈(0,1).Here we shall give some basic notions and notations used in q-calculus.Let x∈C,and n∈N.The q-analogue of x and the q-factorial of n are de fined,respectively,by

and
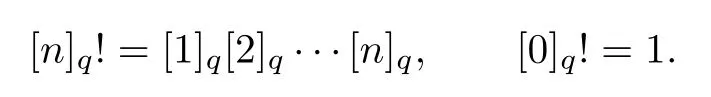
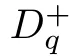
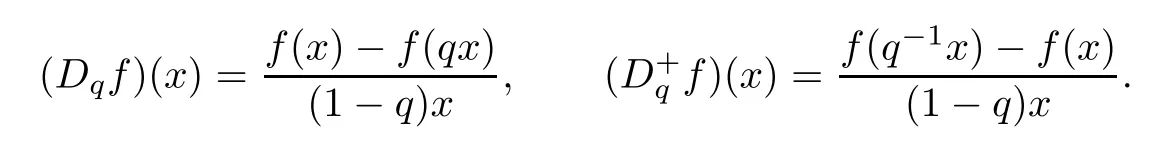
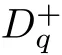
Suppose that 0 provided that the series on the right converges absolutely.Also, The improper q-integral is de fined by provided,again,that the series on the right converges absolutely.For a systematic study of basic properties of q-calculus,one may refer to[3,20]. In this section,we give a brief introduction of(p,q)-calculus.Throughout this paper we shall take 0 Suppose that 0 and the improper(p,q)-integral is de fined by provided that all the series involved are absolutely convergent. Note that when p=1,most of the notions in(p,q)-calculus reduce to the corresponding notions of q-calculus.For more on(p,q)-calculus,one may refer to[8–10]. Remark 2.1 De fine the set Rby For a suitable function f de fined on R,its q-Mellin transform is de fined by Remark 2.2 We mention the following results from[4]: Proposition A then M(f)(s)exists in the strip〈−u,−v〉. Proposition B Next,we will mention some basic properties of the q-Mellin transform;see[4]. Proposition C (b)For s∈〈−β,−α〉, (c)For s∈〈1−β,1−α〉, (d)For s∈〈α,β〉, (e)For s∈〈α+1,β+1〉, Moreover,for n∈N and s∈〈α+n,β+n〉,the following holds: (f)For s∈〈α+1,β+1〉, Moreover,for n∈N and s∈〈α+n,β+n〉,the following holds: (g)For s∈〈α−1,β−1〉, (h)Given ρ>0 and s∈〈ρα,ρβ〉,we have that (i)Let{µ}be a sequence in R,let{λ}be a sequence in C,and let f be a suitable function.Then provided that the sum converges. Lemma D where The inversion formula for the q-Mellin transform is given by the following theorem: Theorem E The q-Mellin convolution product of two functions f and g is de fined by provided that the q-integral exists. The q-Mellin convolution is a commutative operation.Moreover,the q-Mellin convolution equality holds.More precisely,the following is known: Proposition F (i)f∗g=g∗f; (ii)M[f∗g]=M(f)M(g). We also have that the following Parseval-type relations hold: Proposition G De fine the set Rby De finition 3.1 Remark 3.2 (ii)There exists a(possibly empty)maximal open vertical strip in which the integral(3.1)is well de fined.We denote it by〈α,β〉and call it a fundamental strip,or simply a strip. We shall be using the following result,which is also of independent interest,and which gives a relation between the q-integral and(p,q)-integral: Proof and we are done. By using Lemma 3.3,it can be proved that the q-Mellin transform and the(p,q)-Mellin transform are related.Indeed,the following can be proved: We now prove Proposition 3.5 Proof The next theorem provides some of the basic properties of the(p,q)-Mellin transform.The proof can be obtained in view of the de finition of the(p,q)-Mellin transform,Lemmas 3.3 and 3.4,and Proposition C. Theorem 3.6 (b)For s∈〈−β,−α〉,we have that (c)For s∈〈1−β,1−α〉,we have that (d)For any a∈R,s∈〈α−a,β−a〉,we have that (e)For s∈〈α,β〉,we have that (f)For s∈〈α+1,β+1〉,we have that (g)For s∈〈α+1,β+1〉,we have that (h)For s∈〈α−1,β−1〉,we have that (i)Given ρ>0 and s∈〈ρα,ρβ〉,we have that (j)Let{µ}be a sequence in R,let{λ}be a sequence in C and let f be a suitable function.Then we have that provided that the sum converges. (k)For a,b∈R and s∈〈α,β〉∩〈α,β〉,we have that Remark 3.7 (a)For second order derivative,it holds that for s∈〈α+2,β+2〉,we have and therefore,proceeding as in(a)above,we get that For general n∈N,we conjecture that for s∈〈α+n,β+n〉,the following holds: (ii)Similarly,the expression(3.3)can be obtained for higher order derivatives as well.The following can be proved: Again,for general n∈N,we conjecture that for s∈〈α+n,β+n〉,the following holds: Theorem 4.1 The above series converges uniformly with respect to s,so that we can change the order of integration and summation.Therefore,by using Lemma D with q replaced by q/p,and making a variable substitution,we get and the assertion follows. Next,we de fine the appropriate convolution for the(p,q)-Mellin transform. De finition 4.2 provided that the(p,q)-integral exists. We now prove some of the properties of the convolution de fined above. Next,we prove the Parseval type relation for the(p,q)-Mellin transform. Proposition 4.4 Proof Proposition 4.5 Proof Now the assertion follows by taking x=1 in the last equality and by applying the de finition of convolution. In this section we will solve a(p,q)-integral equation with the help of the(p,q)-Mellin transform.We begin with the following lemma: Now,applying the inversion formula,we have that and it follows,in view of Propositin 4.4,that(5.5)is a solution of(5.4). Moreover,if(5.6)is satis fied,then L=K,and we are done. Along similar lines,by using Lemma 5.1(ii),we can immediately obtain the following: Theorem 5.3 then the integral equation has a solution Finally,we prove a result which is the(p,q)-analogue of the Titchmarsh Theorem[19]. Proof then(5.7)takes the form Applying Lemma 5.1 to both of these equations,we have that Changing s into 1−s in one of these equations and multiplying with the other,we get the desired result. In this paper,we have introduced and studied the(p,q)-Mellin transform,which generalizes the known notion of q-Mellin transform.In this regard,the corresponding convolution has been de fined and the inversion formula has been derived.In terms of applications of the(p,q)-Mellin transform,we have solved some integral equations.Moreover,a(p,q)-analogue of the Titchmarsh theorem has also been derived.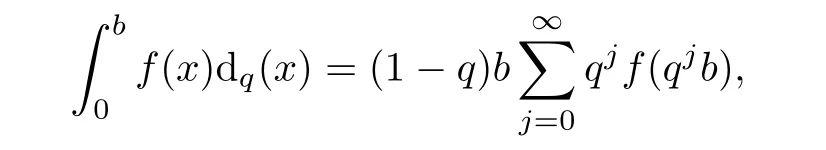
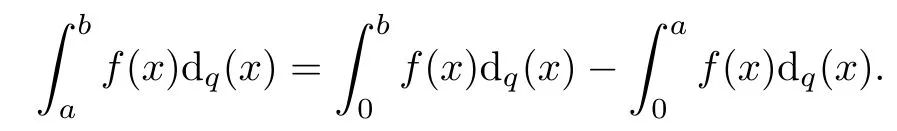
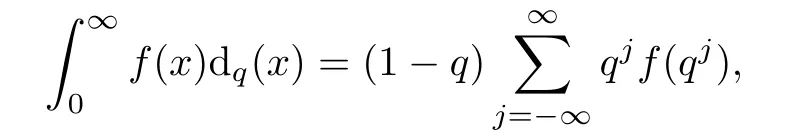
2.2 (p,q)-Calculus
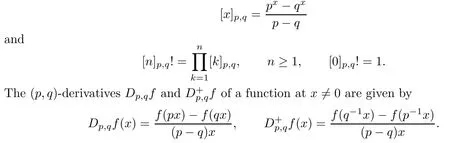
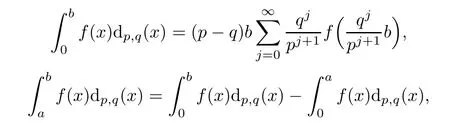
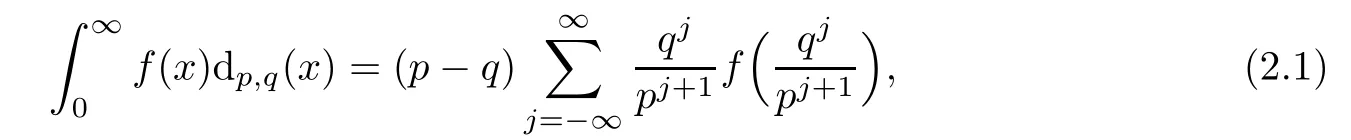

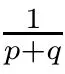
2.3 q-Mellin Transform
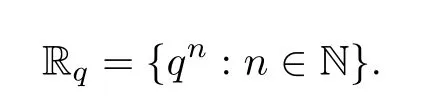
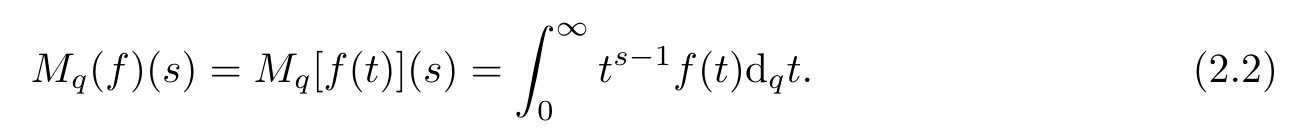

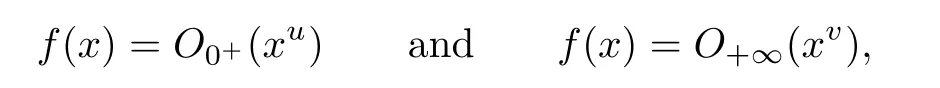
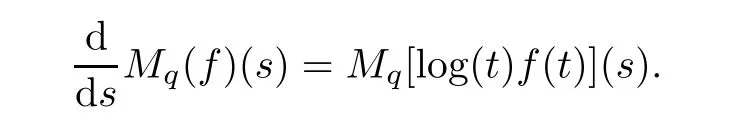

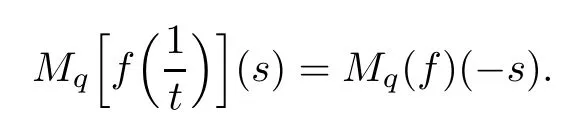
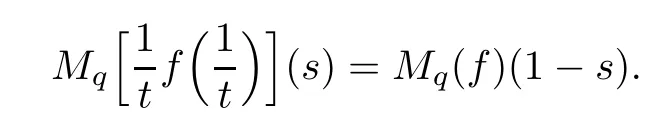

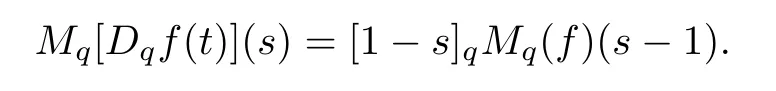
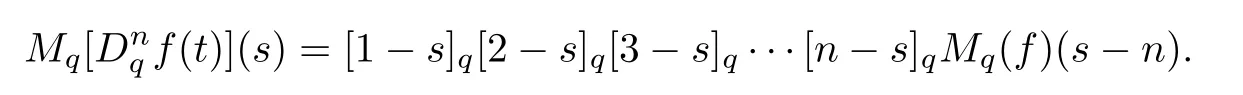
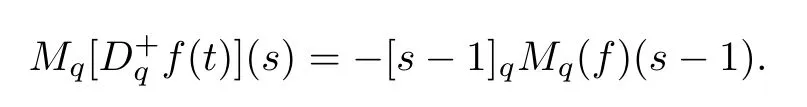
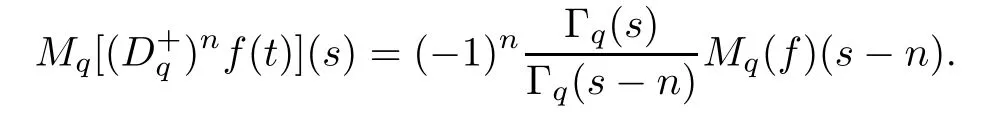
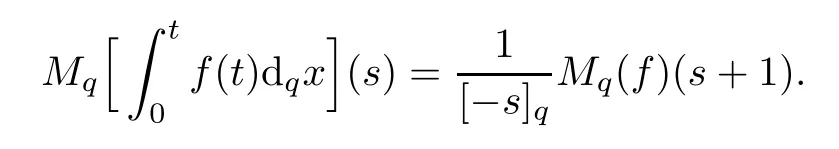
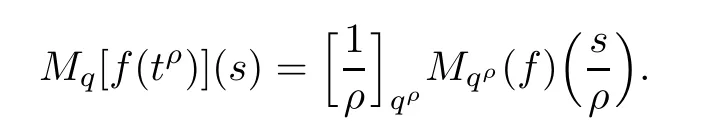
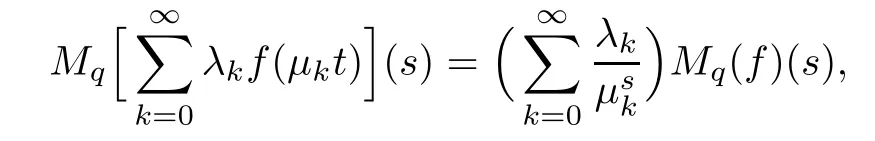
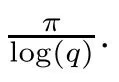
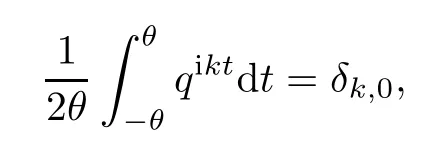

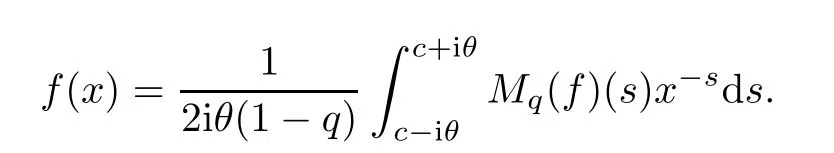
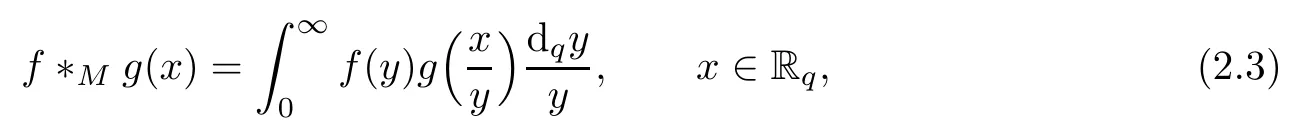

3 The(p,q)-Mellin Transform

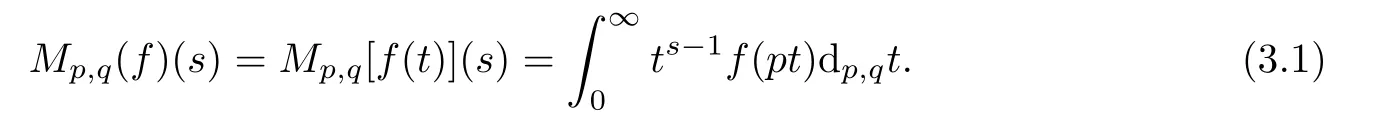
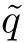
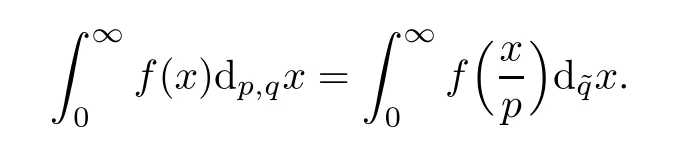
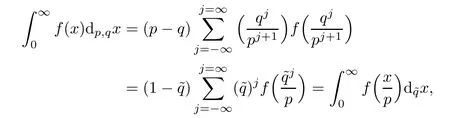
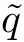
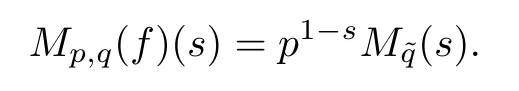
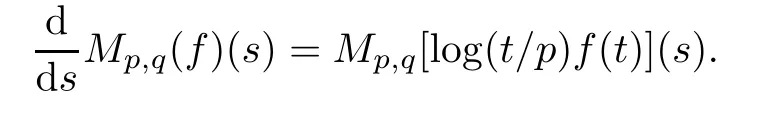

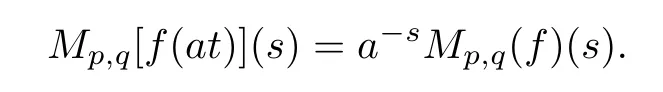
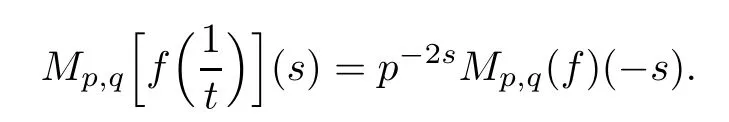
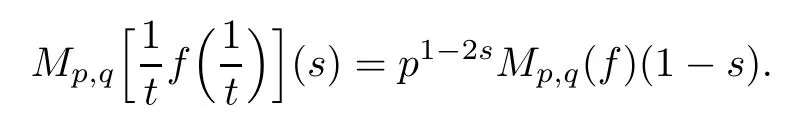
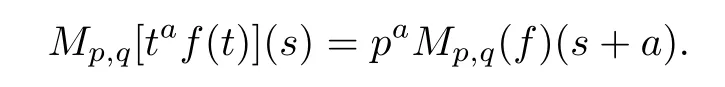
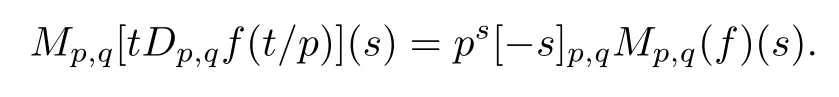
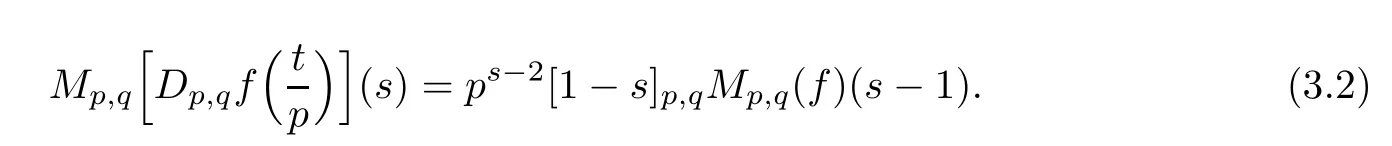
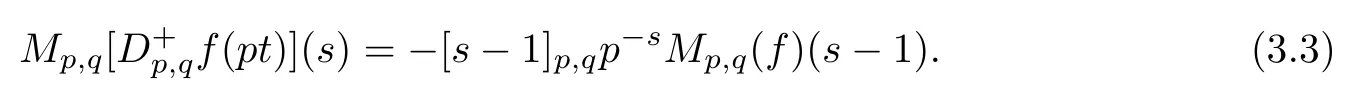
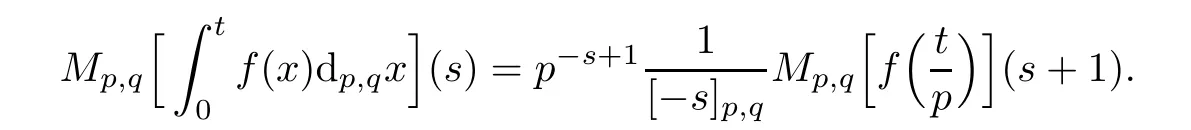
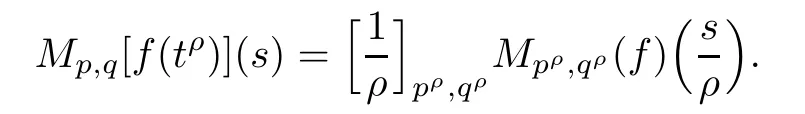
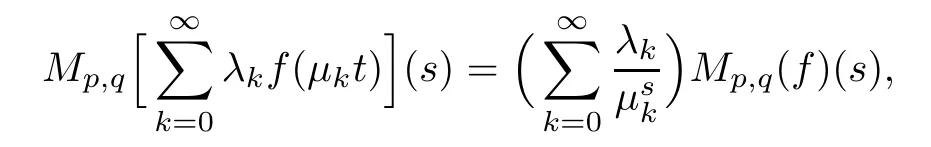
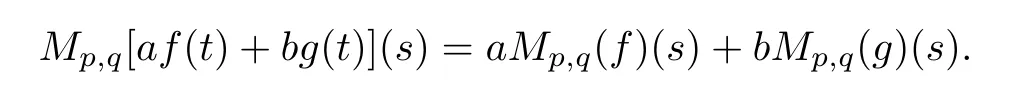

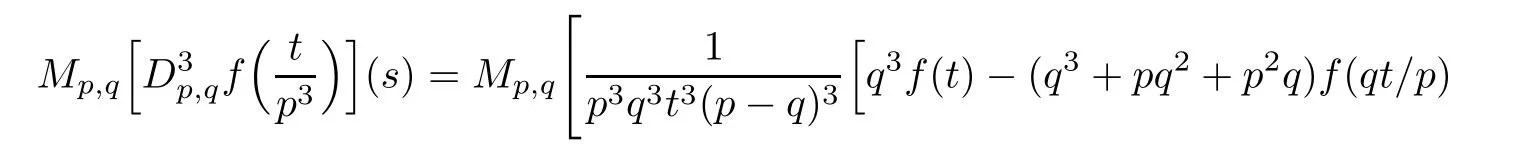

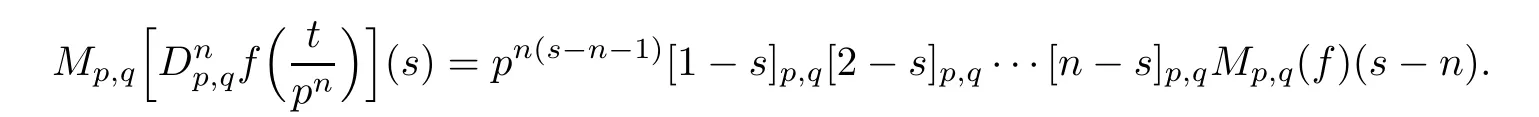
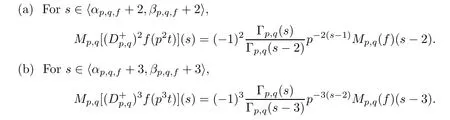
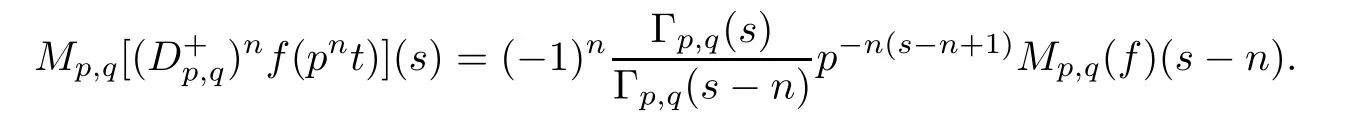
4 Inversion Formula and Convolution
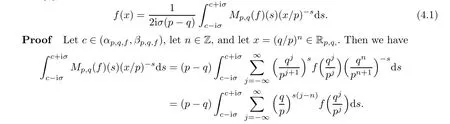
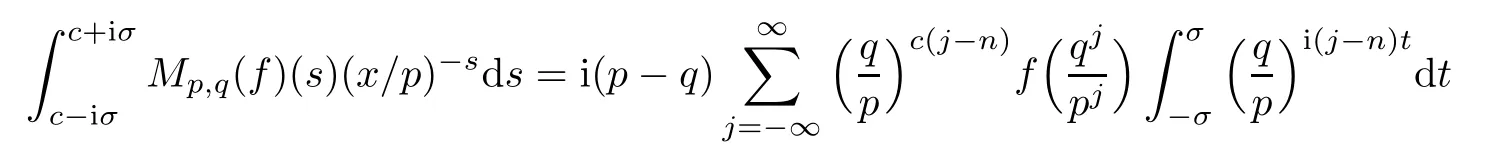

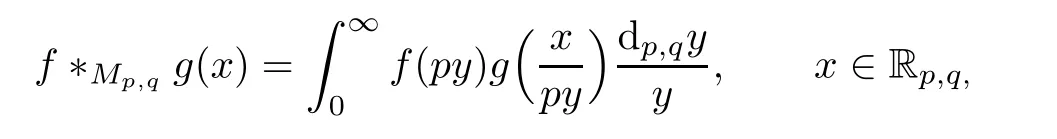

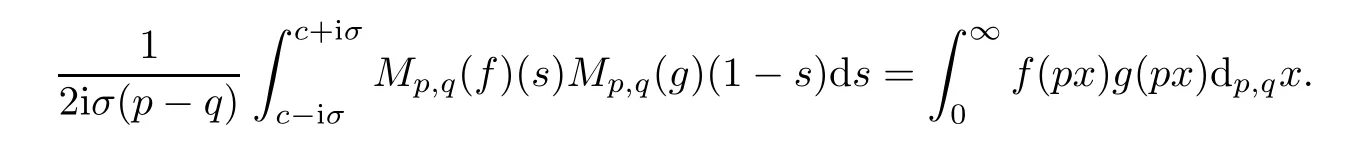
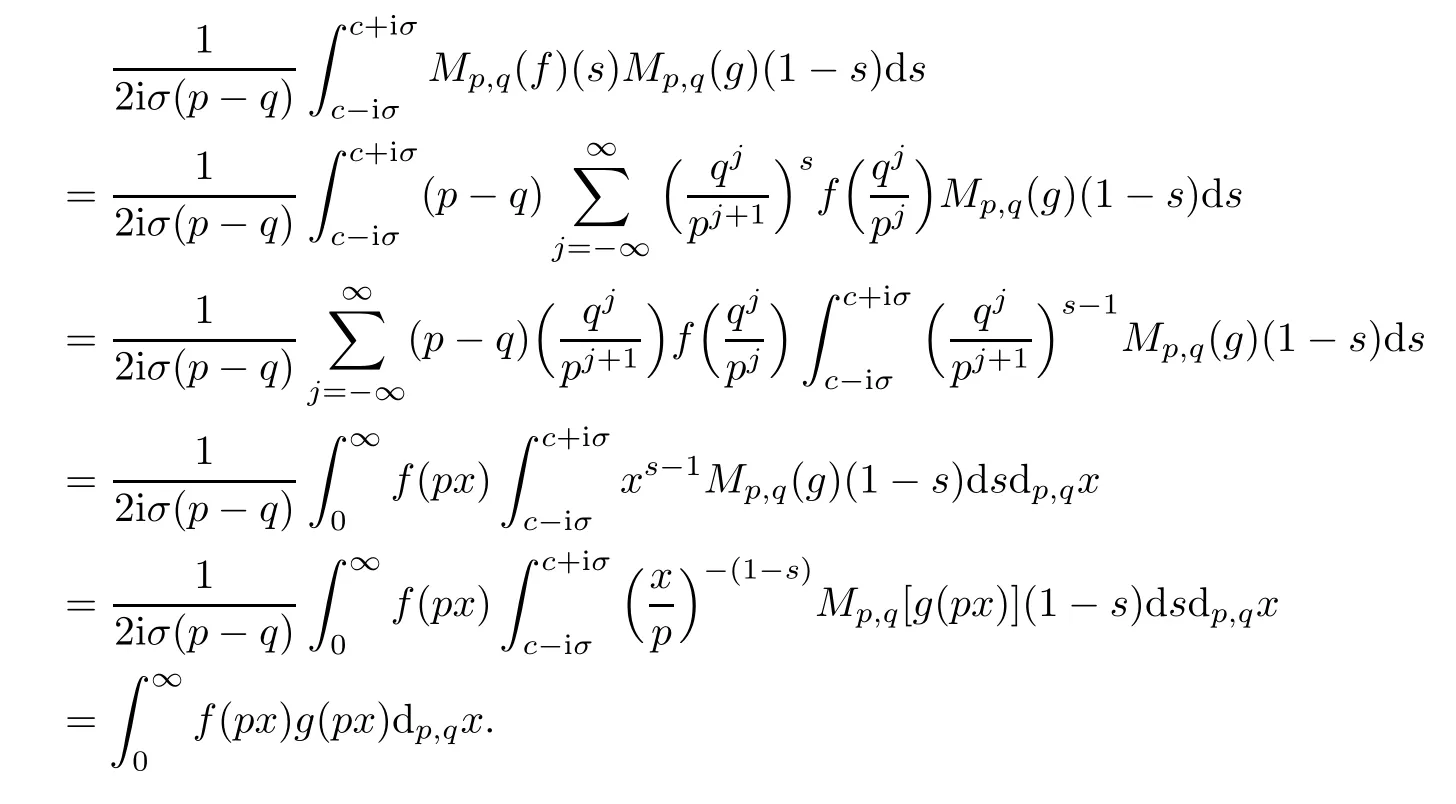
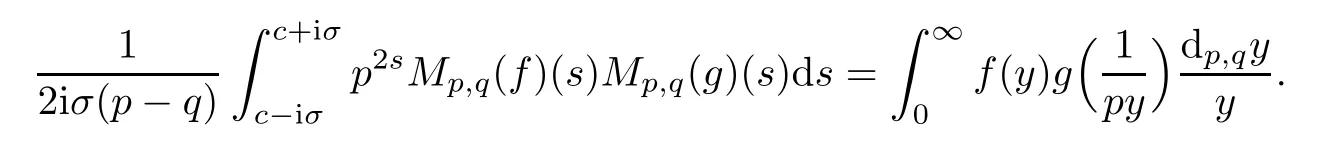
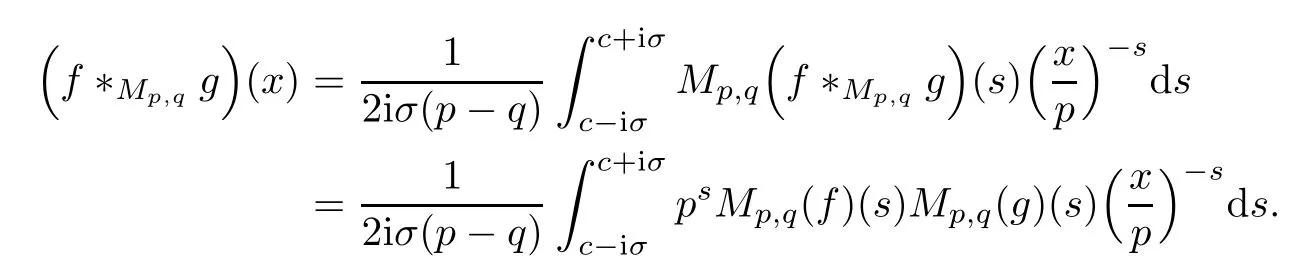
5 Applications
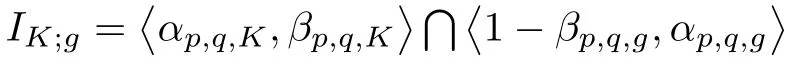


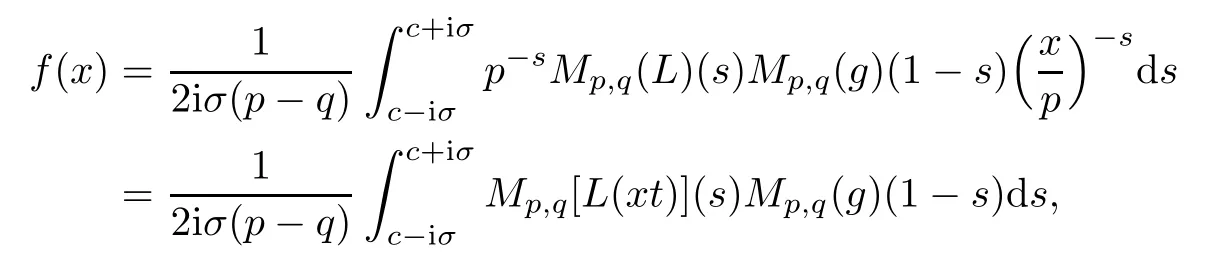
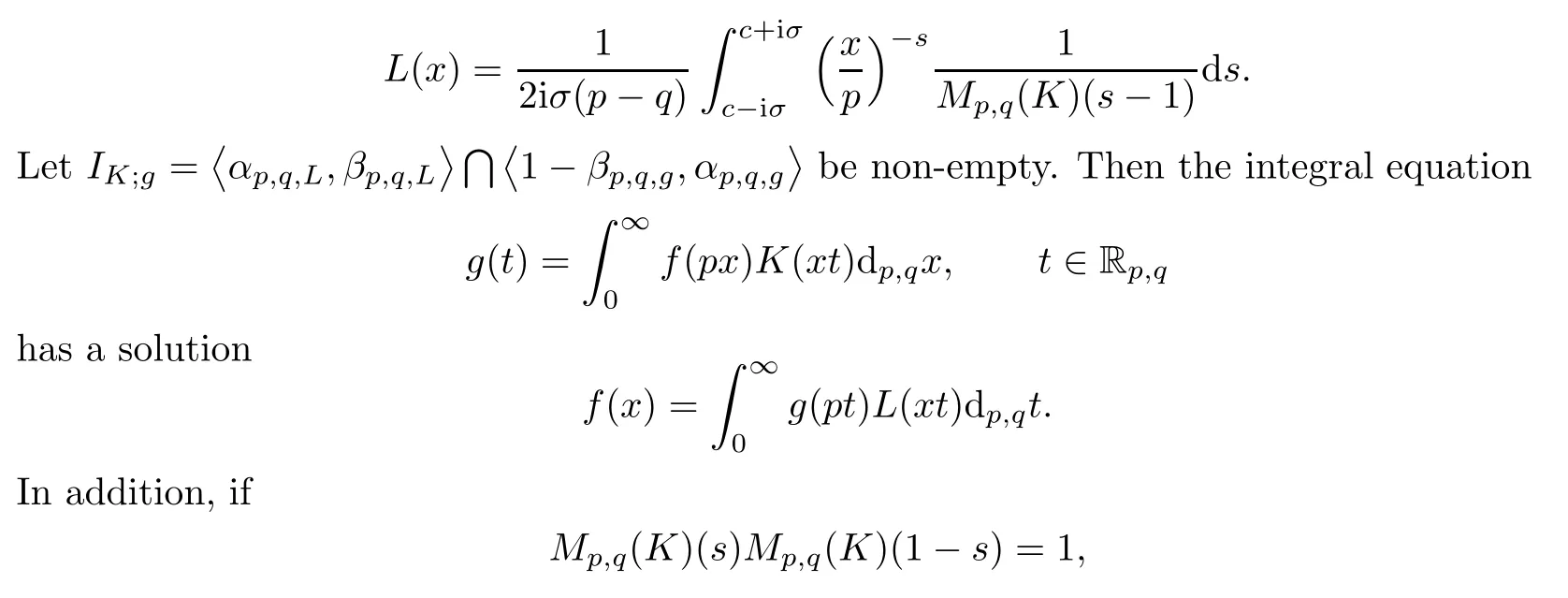
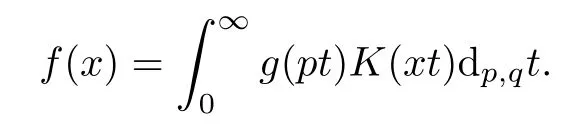
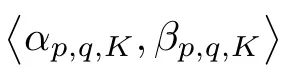
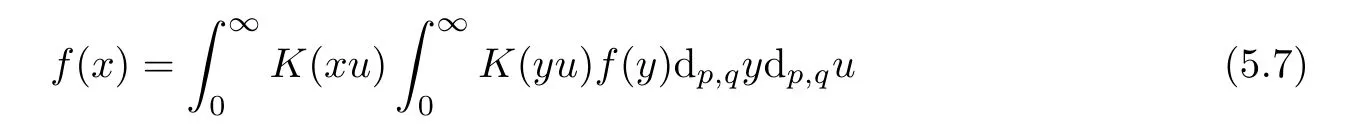
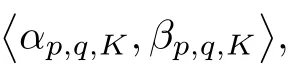
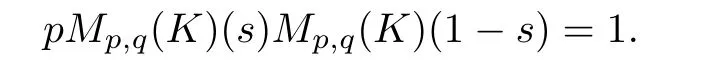
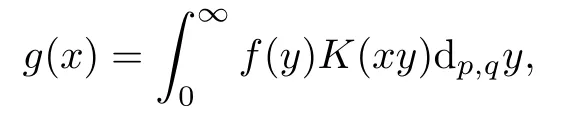
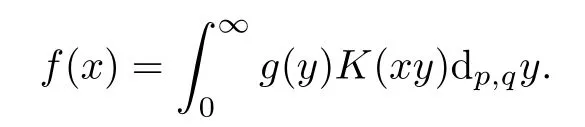
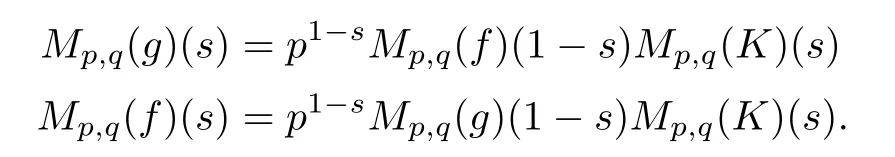
6 Conclusion
 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
