ADDITIVE MAPPINGS PRESERVING FREDHOLM OPERATORS WITH FIXED NULLITY OR DEFECT∗
Ruihan ZHANG(张芮涵)Weijuan SHI(史维娟) Guoxing JI(吉国兴)
School of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710119,China
E-mail:ruihan@snnu.edu.cn;shiweijuan1016@163.com;gxji@snnu.edu.cn
Abstract Let X be an in finite-dimensional real or complex Banach space,and B(X)the Banach algebra of all bounded linear operators on X.In this paper,given any non-negative integer n,we characterize the surjective additive maps on B(X)preserving Fredholm operators with fixed nullity or defect equal to n in both directions,and describe completely the structure of these maps.
Key words Fredholm operator;additive preserver;nullity;defect
1 Introduction
Linear or additive preserver problems aim to characterize linear or non-linear maps on operator algebras preserving certain properties,subsets or relations.For excellent expositions on these problems,we refer the interested reader to[1–10]and the references therein.One of the most famous problems in this direction is Kaplansky’s problem[11],which asks whether every surjective unital invertibility preserving linear map between two semi-simple Banach algebras is a Jordan homomorphism.This problem was solved in some special cases of semi-simple Banach algebras.Several authors have studied linear maps which preserve the class of semi-Fredholm operators,Fredholm operators and the related operators in both directions([8,9,12–15]).It has been shown that such maps preserve the ideal of compact operators in both directions,and that the maps induced by them on the Calkin algebra are Jordan automorphisms.In[13],the authors characterized additive maps on B(X)preserving Drazin invertible operators of index n.It was shown in[14]that given an interger n≥1,if the surjective additive map Φ:B(X)→B(X)preserves the set of semi-Fredholm operators on X of non-positive index and a dimension of the kernel less than n,then Φ(T)=UTV for all T or Φ(T)=UTV for all T,where U and V are two bijective bounded linear,or conjugate linear,mappings between suitable spaces.On the other hand,it is known that the nullity and defect of an operator are fundamental and key aspects of the Fredholm theory.In this paper,combining Fredholm operators with the nullity and defect,we consider surjective additive maps that preserve the class of Fredholm operators with fixed nullity or defect,and give a complete description of these maps.
Throughout this paper,X(resp.Y)denotes an in finite-dimensional Banach space over K=R or C.Let B(X)be the algebra of all bounded linear operators acting on X,and let Xbe the dual space of X.For an operator T,we denote the kernel and range of T by ker(T)and ran(T),respectively.We write Tfor its adjoint on the topological dual space X.Recall that an operator T is called semi-Fredholm if ran(T)is closed and either dimker(T)or codim ran(T)is finite.For such an operator T,if ran(T)is closed and dimker(T)<∞as well as codim ran(T)<∞,then T is said to be Fredholm.For a Fredholm operator T,the dimension of its kernel is said to be the nullity of T,and the codimension of its range is said to be the defect of T.
Given any integer n≥0,we introduce the class of Fredholm operators with fixed nullity or defect:

Denote by S(X)(resp.S(Y)),or S without any confusion,any one of the sets A(X)(resp.A(Y))or Q(X)(resp.Q(Y)).We shall say that a surjective map ϕ:B(X)→B(Y)preserves S in both directions if ϕ(T)∈S(Y)⇔T∈S(X).
In this paper,we will provide a detailed characterization of a surjective additive map ϕ on B(X)preserving A(X)(resp.Q(X))in both directions.
2 Main Results
In this section,let S(X)be any one of the sets A(X)or Q(X).As usual,let x∈X and f∈Xbe nonzero.We denote by x⊗f the bounded linear rank one operator de fined by(x⊗f)z=f(z)x for all z∈X.Now,we give our main results.
Theorem 2.1
Let ϕ:B(X)→B(Y)be a surjective additive map and let n be a nonnegative integer.Then ϕ preserves S in both directions if and only if one of the following assertions holds:(i)there exist two bijective bounded linear or conjugate linear mappings A:X→Y and B:Y→X such that ϕ(T)=ATB for all T∈B(X);
(ii)there exist two bijective bounded linear or conjugate linear mappings C:X→Y and D:Y→Xsuch that ϕ(T)=CTD for all T∈B(X).In this case,X and Y are re flexive,and every Fredholm operator on X has index 0.
Note that the second case may occur.For example,Argyros and Haydon[16]have shown that there exists an in finite-dimensional Banach space X such that every operator T∈B(X)can be written as λI+K where λ is a scalar and K is a compact operator.Clearly,in such spaces,the additive map ϕ(T)=CTD preserves S in both directions.
The proof of this theorem requires some auxiliary results which will be given at the end of this section.We establish these useful results as follows:
Proposition 2.2
Let T∈S(X)and F be a rank one operator such that T+F∈S(X).Then either T+2F∈S(X)or T−2F∈S(X).Proof
Note that T is Fredholm,since T∈S(X);as such,so are T+F,T+2F and T−2F.(i)Suppose that T∈A(X).Note that F is a rank one operator.We know,by[17,Lemma 5],that the map λ→dimker(T+λF)is constant on Q minus at most one point.Since
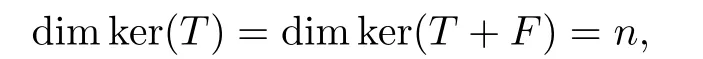
we obtain that

It follows that either T+F∈A(X)or T+2F∈A(X).
(ii)Suppose that T∈Q(X).We have,again by[17,Lemma 5],that the map λ→codim ran(T+λF)is constant on Q minus at most one point.Since
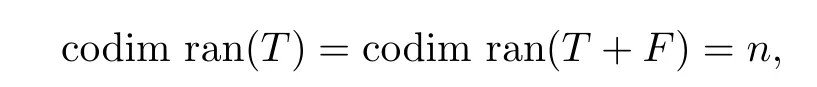
we obtain
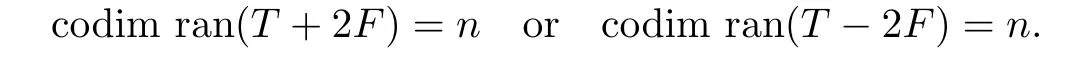
Hence,T+2F∈Q(X)or T−2F∈Q(X).
Recall that an operator is said to be Weyl if it is Fredholm of index zero.The following proposition can help us to establish that every surjective additive map ϕ preserving S in both directions is bijective and preserves rank one operators in both directions:
Proposition 2.3
Let T∈B(X)be a non-zero operator.Then the following assertions hold:(i)there exists a Weyl operator S∈S(X)such that S+2T/∈S(X);
(ii)if dim ran(T)≥2,then there exists a Weyl operator S∈S(X)such that S+T∈S(X),S+2T/∈S(X)and S−2T/∈S(X).
Proof
First,suppose that ran(T)is in finite dimensional.Then codimker(T)=∞.Let x(1≤i≤2n)and y(1≤k≤2n+2)be linearly independent vectors such that the subspace generated by these vectors has trivial intersection with ker(T).It follows that the vectors Tx(1≤i≤2n)and Ty(1≤k≤2n+2)are linearly independent.Take two closed subspaces H and K of X such that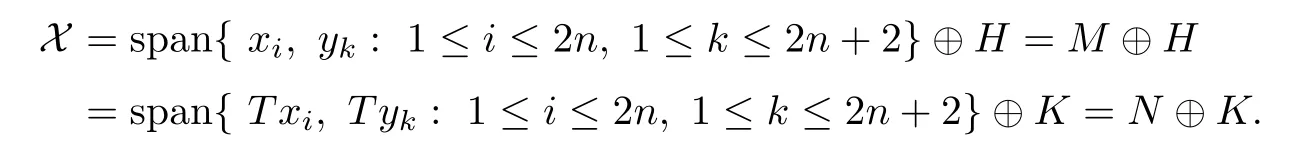
Under the above space decomposition,the operator T can be expressed as
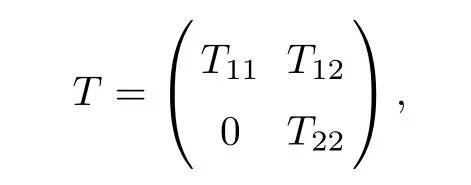
where T∈B(M,N),T∈B(H,N)and T∈B(H,K).Since dimM=dimN<∞,it follows that there exists a bounded linear invertible operator U∈B(K,H).In fact,let L=span{x,Tx,y,Ty:1≤i≤2n,1≤k≤2n+2}and select E⊂X so that X=L⊕E.The subspace L may in turn be written as L=M⊕Mand L=N⊕N.Since L is finite-dimensional with M and N having the same dimension,it follows that the two finite-dimensional subspaces Mand Nalso have the same dimension.Then there must exist an invertible map Umapping Nonto M.Note that the subspaces K and H can be written as K=N⊕E and H=M⊕E.With respect to this decomposition,we de fine an invertible operator U:K→H as follows:
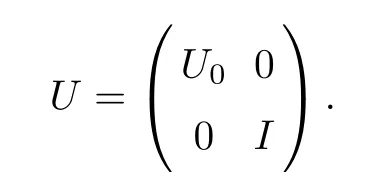
Thus UT∈B(H).Take a λ∈C such that both λI+UTand λI±2UTare invertible.We have that both λU+Tand λU±2Tare invertible.Consider an operator S∈B(X)represented as
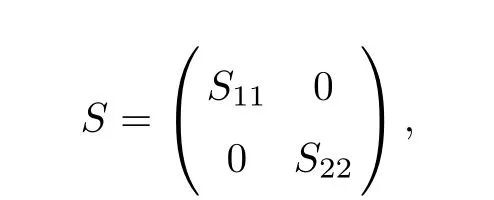
where

and S=λU.Note that Sis of finite rank and dimker(S)=codim ran(S)=n.Combining this with the invertibility of S,we get that S is Fredholm and dimker(S)=codim ran(S)=n.It follows that S is a Weyl operator and that S∈A(X)∩Q(X).Note that
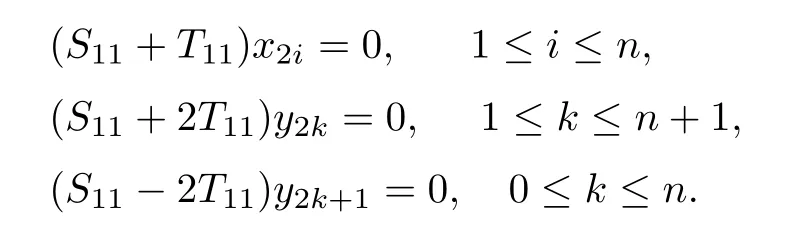
Because of the invertibility of λU+Tand λU±2T,it is known that dimker(S+T)=dimker(S+T)=n and dimker(S±2T)=dimker(S±2T)=n+1.Since
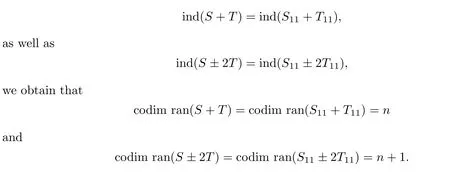
These mean that S+T∈S and S±2T/∈S.
Now,suppose that T is of finite rank and put
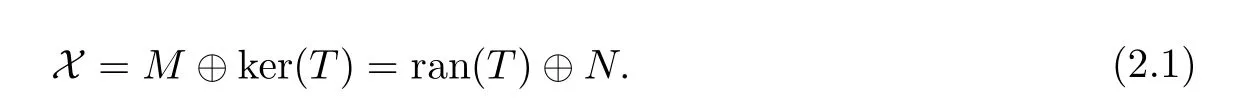
If dim ran(T)≥2,then dimM≥2.Note that the two finite-dimensional subspaces M and dim ran(T)have the same dimension.Let M=span{x,x,···,x}.It follows that ran(T)=span{Tx,Tx,···,Tx}.With respect to the above space decomposition,the operator T is expressed in the following form:
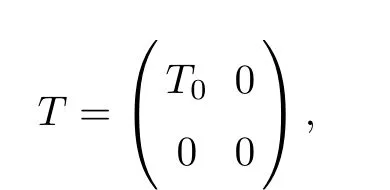
where Tx=Tx,1≤i≤k.
Put
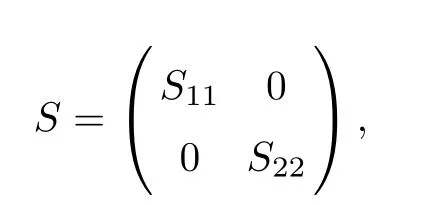
where Sx=2Tx,Sx=−2Tx,Sx=Tx,3≤i≤k if k>2;S:ker(T)→N is Fredholm with dimker(S)=codim ran(S)=n.Note that the subspaces ker(T)and N can be written as ker(T)= J⊕Jand N= Q⊕Q,where the subspaces J and Q are n-dimensional subspaces,respectively.Using a similar argument as to that for the existence of the invertible operators U,we obtain invertible operators U:J→Q.According to the above decomposition,we de fine an invertible operator S:ker(T)→N as follows:

Therefore dim ker(S)=codim ran(S)=n.It follows that S is a Weyl operator and S∈A(X)∩Q(X)again.Note that(S+2T)x=0 and(S−2T)x=0.We have that x∈ker(S+2T),x∈ker(S−2T)and S+Tis invertible.Hence,

Finally,we can get that S+T∈S and S±2T/∈S.This completes the proof of(ii).
If dimran(T)=1,then codimker(T)=1.Under the space decomposition(2.1),we have dimM=1.Thus we can find an invertible operator S:M→ran(T)the same as before.T is similarly expressed in the following form:
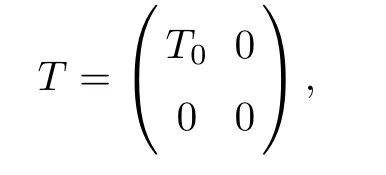
where Tx=Tx,x∈M.
We again de fine an operator S as
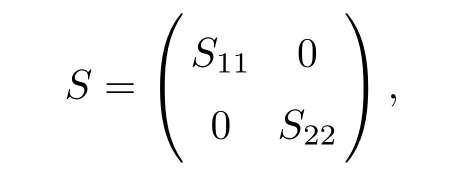
where Sx=−2Txand S:ker(T)→N is a Fredholm operator and

Therefore,dimker(S)=codim ran(S)=n.This also implies that S is a Weyl operator and S∈A(X)∩Q(X).Note that x∈ker(S+2T).Then
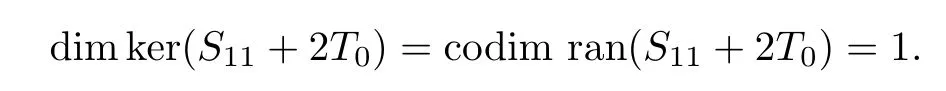
Hence,
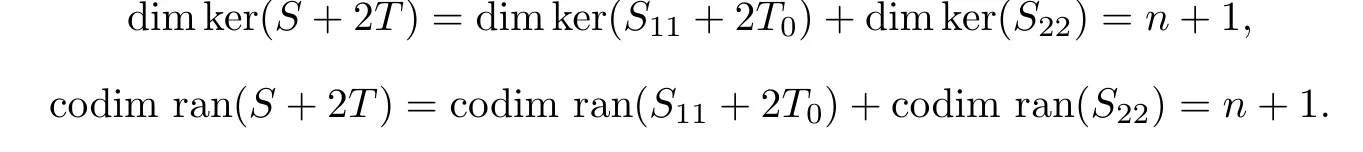
Therefore,S+2T/∈S.This completes the proof of(i).
Proposition 2.4
Let ϕ:B(X)→B(Y)be a surjective additive map that preserves S in both directions.Then(i)ϕ is injective;
(ii)ϕ preserves the set of rank one operators in both directions.
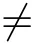
(ii)Let T∈B(X)with dim ran(T)≥2.Then it follows again by Proposition 2.3 that there exists an operator S∈S such that
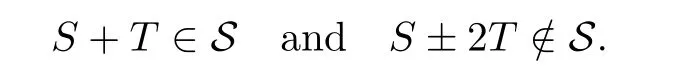
Thus
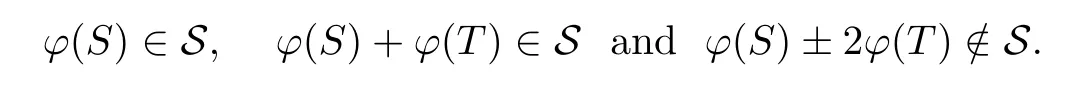
Therefore,we obtain by Proposition 2.2 that dim ran(ϕ(T))≥2.Since ϕ is bijective and ϕsatis fies the same properties as ϕ,we obtain that ϕ preserves the set of rank one operators in both directions.
Let τ be a ring automorphism of K.An additive map A:X→Y is said to be τ-quasilinear if A(λx)=τ(λ)Ax for all λ∈K and x∈X.Notice that in the real case,all the quasilinear maps are linear because the identity is the only ring automorphism of R,while in the complex case,the continuous ring automorphisms are the identity and the complex conjugation.
The following corollary is a straightforward consequence of Proposition 2.4(ii)and[18,Theorems 3.1 and 3.3]:
Corollary 2.5
Let ϕ:B(X)→B(Y)be a surjective additive map which preserves S in both directions.Then there exist a ring automorphism τ and either τ-quasilinear bijective mappings W:X→Y and G:X→Ysuch that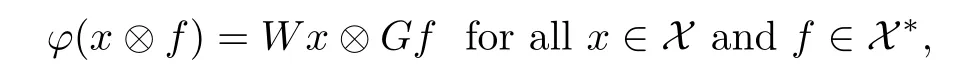
or τ-quasilinear bijective mappings W:X→Yand G:X→Y such that
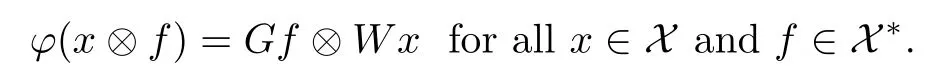
Before giving the proof of the next proposition,we shall first denote by F(X)the set of all operators F∈B(X)with dim ran(F) Proposition 2.6 Proof we get that S+F=ϕ(I+K)/∈A(X).Because I+K is Fredholm and we similarly obtain that S+F=ϕ(I+K)/∈Q(X).Thus S+F/∈S. Next we prove that S is Fredholm.Firstly note that for every rank n idempotent operator P,I−P is Fredholm and It follows,by Corollary 2.5,that I−P∈S and that ϕ(P)is still a rank n operator.Thus S−ϕ(P)=ϕ(I−P)∈S.This implies that S−ϕ(P)is Fredholm.Note that a finite rank perturbation of Fredholm operator is again a Fredholm operator.Then S is Fredholm. Suppose that S is A(X).If ϕ preserves A(X)in both directions,we show that S is invertible.Now,we claim that S is injective.Suppose,to the contrary,that S is not injective.We shall discuss three cases. Case 1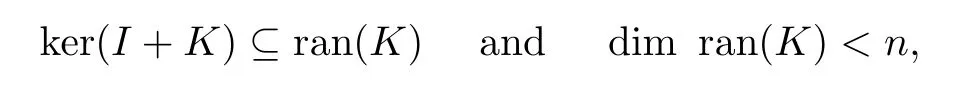

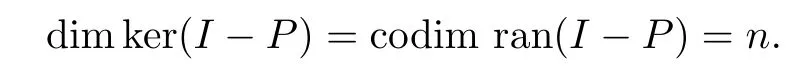
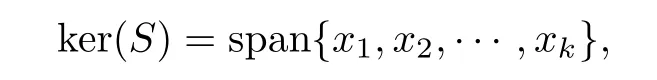
where k We de fine an operator F∈B(X)by Clearly,F∈F(X).We also have dimker(S+F)=n.Because S is a Fredholm operator,it follows that S+F is Fredholm.Therefore S+F∈A(X),which is a contradiction. Case 2 For every rank n idempotent operator P,we have that ϕ(P)is a rank n operator and dimker(S−ϕ(P))=n.For every rank one operator x⊗f,x∈X and f∈X,by Corollary 2.5,there exist a ring automorphism τ and either τ-quasilinear bijective mappings W:X→Y and G:X→Ysuch that ϕ(x⊗f)=Wx⊗Gf or τ-quasilinear bijective mappings W:X→Yand G:X→Y such that ϕ(x⊗f)=Gf⊗Wx. Suppose that ϕ(x⊗f)=Wx⊗Gf.Since S is Fredholm,we have dimker(S)<∞.Denote where W:X→Y,G:X→Yare τ-quasilinear bijective mappings,and ran ϕ(P)=span{Wx,Wx,···,Wx}.Clearly,ϕ(P)|=0.Then,for every y∈ker(S),we have(S−ϕ(P))y=0.Note that dimker(S)>n.Then dimker(S−ϕ(P))>n,which is the desired contradiction. Suppose that ϕ(x⊗f)=Gf⊗Wx.Then,using a similar argument,we again get a contradiction. Case 3 This means that S∈A(X),whence I∈A(X),which is a contradiction. Therefore,S is injective.Next we will prove that S is surjective. Now suppose that S is Q(X).If ϕ preserves Q(X)in both directions,since S is Fredholm,we have that Sis Fredholm.Noting that codim ran(S−ϕ(P))=dimker(S−ϕ(P)),it follows that dimker(S−ϕ(P))=n for every rank n idempotent operator P.From a similar discussion to that in the above case,we get the invertibility of the operator S.That is to say,S is invertible. Therefore,ϕ(I)is invertible. Proof of Theorem 2.1 Case 1 Case 2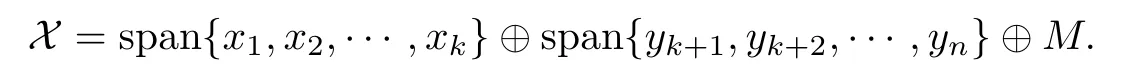
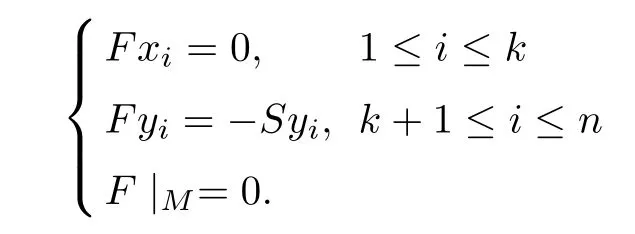
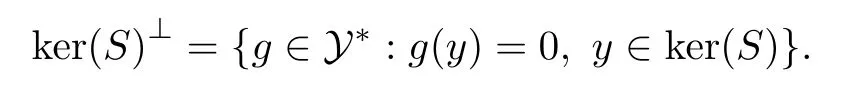
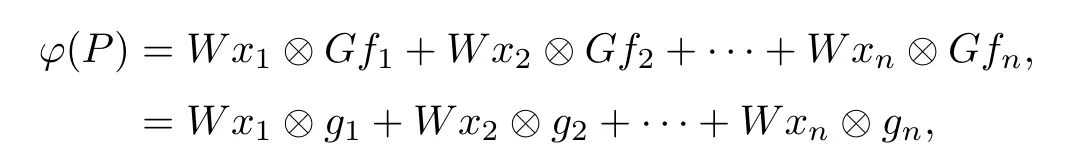
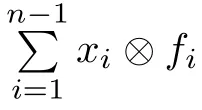
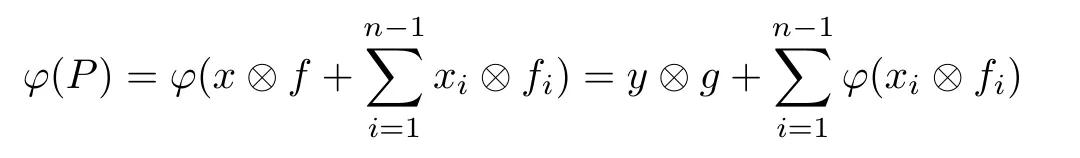
 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
- Acta Mathematica Scientia(English Series)的其它文章
- RIGIDITY RESULTS FOR SELF-SHRINKING SURFACES IN R4∗
- GLOBAL STRONG SOLUTION AND EXPONENTIAL DECAY OF 3D NONHOMOGENEOUS ASYMMETRIC FLUID EQUATIONS WITH VACUUM∗
- CONTINUOUS TIME MIXED STATE BRANCHING PROCESSES AND STOCHASTIC EQUATIONS∗
- SOME OSCILLATION CRITERIA FOR A CLASS OF HIGHER ORDER NONLINEAR DYNAMIC EQUATIONS WITH A DELAY ARGUMENT ON TIME SCALES∗
- COARSE ISOMETRIES BETWEEN FINITE DIMENSIONAL BANACH SPACES∗
- ZERO KINEMATIC VISCOSITY-MAGNETIC DIFFUSION LIMIT OF THE INCOMPRESSIBLE VISCOUS MAGNETOHYDRODYNAMIC EQUATIONS WITH NAVIER BOUNDARY CONDITIONS∗
