ZERO DISSIPATION LIMIT TO RAREFACTION WAVES FOR THE ONE-DIMENSIONAL COMPRESSIBLE NAVIER-STOKES EQUATIONS WITH SELECTED DENSITY-DEPENDENT VISCOSITY∗
Yifan SU(苏奕帆)Zhenhua GUO(郭真华)
School of Mathematics,CNS,Northwest University,Xi’an 710127,China
E-mail:mayifansu@163.com;zhguo@nwu.edu.cn
Abstract This paper is devoted to studying the zero dissipation limit problem for the onedimensional compressible Navier-Stokes equations with selected density-dependent viscosity.In particular,we focus our attention on the viscosity taking the formµ(ρ)=ρ∊(∊>0).For the selected density-dependent viscosity,it is proved that the solutions of the one-dimensional compressible Navier-Stokes equations with centered rarefaction wave initial data exist for all time,and converge to the centered rarefaction waves as the viscosity vanishes,uniformly away from the initial discontinuities.New and subtle analysis is developed to overcome difficulties due to the selected density-dependent viscosity to derive energy estimates,in addition to the scaling argument and elementary energy analysis.Moreover,our results extend the studies in[Xin Z P.Comm Pure Appl Math,1993,46(5):621-665].
Key words compressible Navier-Stokes equations;density-dependent viscosity;rarefaction wave;zero dissipation limit
1 Introduction
The compressible Navier-Stokes equations with density-dependent viscosity coefficients without external force can be written as
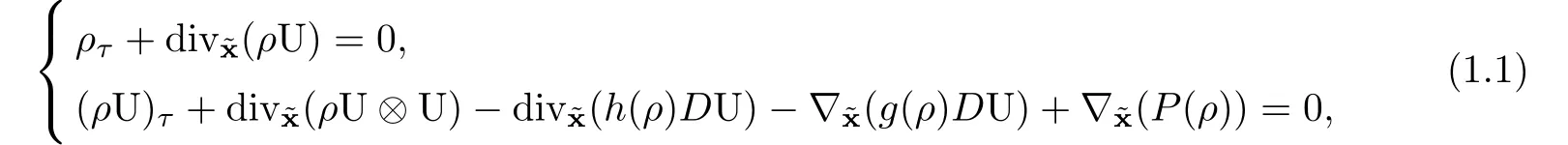
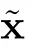
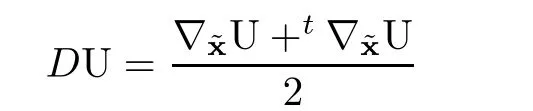
In particular,(1.1)in one-dimensional space can be read as

Let us assume that h(ρ)and g(ρ)are two C(0,∞)functions in(1.2)satisfying

and take

One can find that

In this paper,we intend to study the vanishing viscosity limit of the solution to the onedimensional compressible Navier-Stokes equations(1.2)with(1.5).For convenience,the problem that we investigate is,in the Lagrangian coordinates,the asymptotic behavior of the solutions to the one-dimensional compressible isentropic Navier-Stokes equations with densitydependent viscosity

with the initial conditions
where uand v>0 are given constants,and the pressure p is assumed to be a smooth function of v>0 satisfying

For the Navier-Stokes equations(1.6),formally,as∊tends to zero,the limit system is the following compressible Euler equations:

Note that the condition(1.8)assures that system(1.9)is strictly hyperbolic with two characteristic speeds
and both characteristic fields are genuinely nonlinear.Therefore,there are rarefaction wave solutions to the Euler equations(1.9)which connect a given state(u,v)to a state(u,v)(at least locally).Our main purpose is to show that rarefaction wave solutions to the Euler equations(1.9)are strong limits of solutions to(1.6)in an appropriate sense as viscosity vanishes.
The study of the limiting process of viscous flows when the viscosity tends to zero is one of the important problems in the theory of compressible fluids.When the solution of the inviscid flow is smooth,the zero dissipation limit problem can be solved by the classical scaling method.However,the inviscid compressible flow contains discontinuities,such as shock waves,in general.Therefore,how to justify the zero dissipation limit to the Euler equations with basic wave patterns is a natural and difficult problem.
Let us now review some related previous works.There are,in fact,many results on the vanishing viscosity limit for a compressible fluid.Hoff-Liu[14] first proved the vanishing viscosity limit for a piecewise constant shock even with an initial layer.Goodman-Xin[15] first verifi ed the viscous limit for piecewise smooth solutions separated by non-interacting shock waves using a matched asymptotic expansion method.Later Xin[16]obtained the zero dissipation limit for rarefaction waves without vacuum for both rarefaction wave data and well-prepared smooth data.Then Wang[17]generalized the result of Goodman-Xin[15]to the isentropic Navier-Stokes equations(1.2).Chen-Perepelitsa[18]proved the vanishing viscosity to the compressible Euler equations for the isentropic compressible Navier-Stokes equations with constant viscosity by a compensated compactness method in the case in which the far field of the initial values of the Euler system has no vacuums.For the full Navier-Stokes equations with constant viscosity,there are also many results on the zero dissipation limit to the corresponding full Euler system with basic wave patterns without a vacuum.We refer to Jiang-Ni-Sun[19]and Xin-Zeng[20]for the rarefaction wave,Wang[21]for the shock wave,Ma[22]for the contact discontinuity,Huang-Wang-Yang[23]and Huang-Jiang-Wang[24]for the superposition of two rarefaction waves and a contact discontinuity,Huang-Wang-Yang[25]for the superposition of one shock and one rarefaction wave and Zhang-Pan-Wang-Tan[26]for the superposition of two shock waves with the initial layer,and one can also refer to[27–29].Moreover,Huang-Wang-Wang-Yang[30]succeeded in justifying the vanishing viscosity limit of full compressible Navier-Stokes equations in the setting of Riemannian solutions for the superposition of shock wave,rarefaction wave and contact discontinuity.
This paper is strongly motivated by the work[16],and also deals with the case in which the underlying inviscid flow is a centered rarefaction wave.We prove that the solution of system(1.6)with weak centered rarefaction data exists for all time and converges to the inviscid centered rarefaction wave as the viscosity tends to zero,uniformly away from the initial discontinuity.
Now,we give precise statements of our main theorems.There are two families of rarefaction wavesfor the Euler equations(1.9);the 1-rarefactionwavesare described here.The 1-rarefaction waves are characterized by the fact that the 1-Riemann invariant is constant in(x,t)and the 1-characteristic speed is increasing in x.If the end states(u,v)in(1.7)satisfy
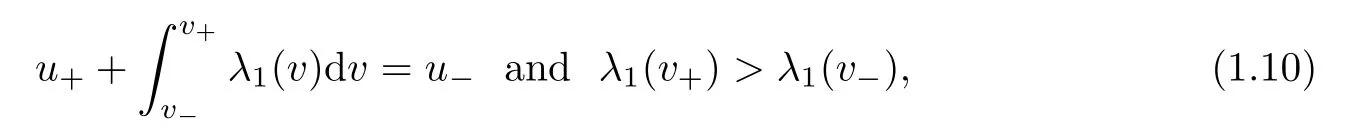
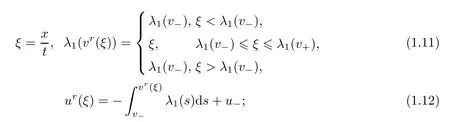
this is uniquely determined by the system(1.9)and the initial rarefaction wave data
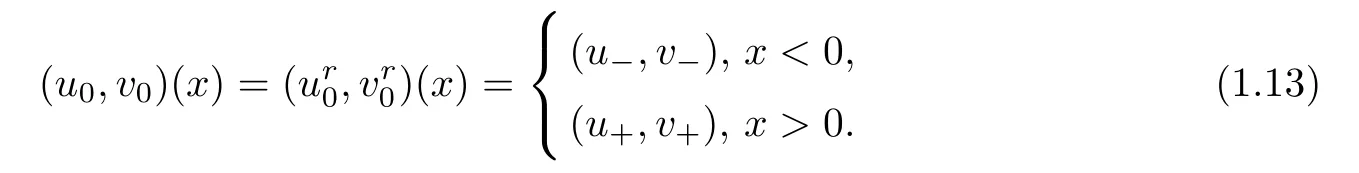
In fact,a centered rarefaction wave is only Lipschitz continuous away from its center.We focus on the compressible Navier-Stokes equations(1.6)with the fixed rarefaction wave initial data
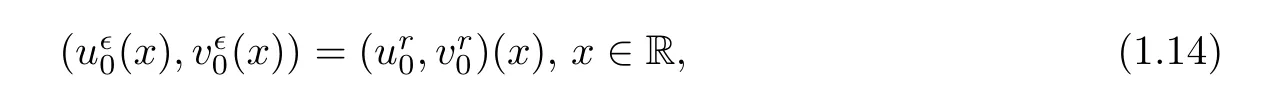
and both the existence and the asymptotic behavior of the solution are studied.
Compared with the previous work[16]on the isentropic Naiver-Stokes equations with constant viscosity,some new difficulties occur for the Navier-Stokes equations(1.6)with densitydependent viscosity considered in the present paper.Dealing with the terms for the densitydependent viscosities becomes subtle.In fact,the derivative estimates of the perturbation of the speci fic volume v depend on the second-order derivative estimates of velocity,which is quite different from the constant viscosity case in[16].
Theorem 1.1
Let the constant states(u,v)with(v>0)be connected by a centered 1-rarefaction wave de fined by(1.11)and(1.12)above,with suitably small strength.Then the compressible Navier-Stokes equations(1.6)with the rarefaction wave initial data(1.14)have a unique,global,piecewise smooth solution(u,v)(x,t).Moreover,the smooth solution(u,v)(x,t)has the following properties:
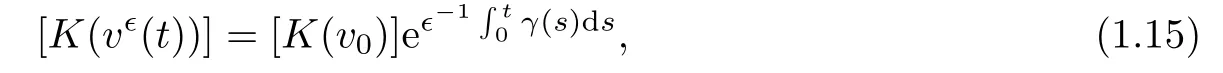
where
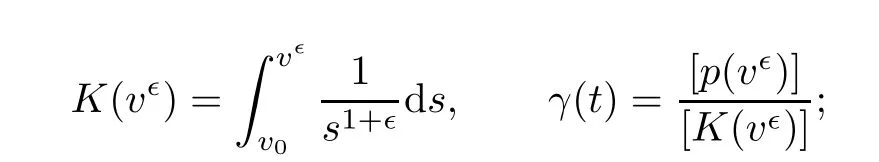
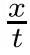
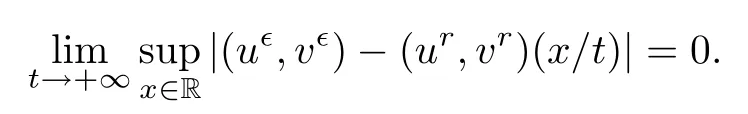
For the Navier-Stokes equation(1.6),the initial discontinuities in the speci fic volume v propagate along the particle paths,but the discontinuities will decay exponentially fast([31,32]).In fact,Theorem 1.1 depends on an interesting part of local existence theory,which concerns the evolution in time of the jump discontinuity.The local existence theory is given in the Appendix.

Theorem 1.2
Let(u,v)(x/t)be the centered 1-rarefaction wave de fined by(1.11)and(1.12),which connects two constant states(u,v)satisfying(1.10)with v>0.Then there exists a positive constant∊such that for each∊∈(0,∊),one can construct a global smooth solution(u,v)(x,t)to(1.6)satisfying
This solution also satis fies the following:(u,v)(x,t)convergesto(u,v)(x/t)pointwise except for at the original point(0,0)as∊→0.Furthermore,for any h>0,there is a constant c(h)>0,independent of∊,such that
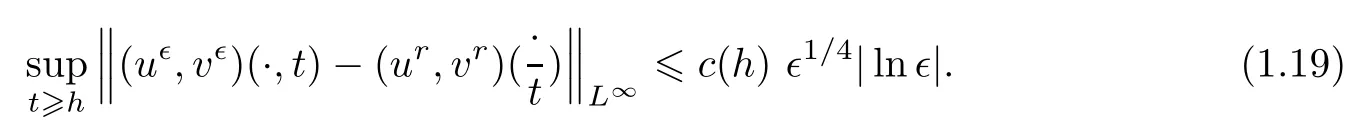
Notations
Throughout this paper,several positive generic constants are denoted by C unless they need to be distinguished,and we de fine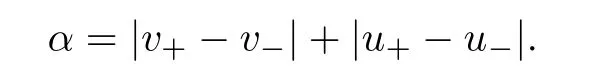
For function spaces,L=L(R)and W=W(R)denote the usual Lebesgue space and k-th order Sobolev space on the whole space R with norms‖·‖and‖·‖,respectively.In particular,H=W(R)with norm‖·‖.[A(τ)]denotes the jump A(0+,τ)−A(0−,τ)in a given quantity A.Moreover,
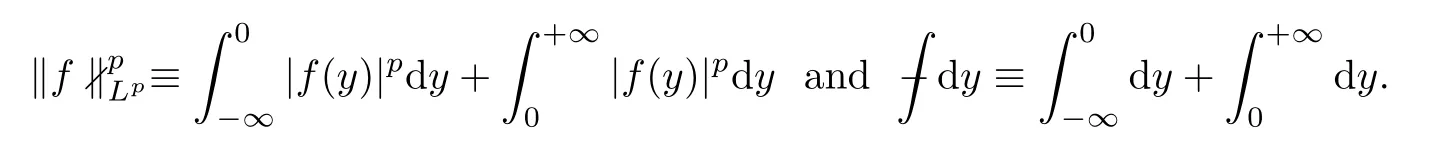
2 Rarefaction Waves
Consider the Riemann problem for the typical Burgers’equation
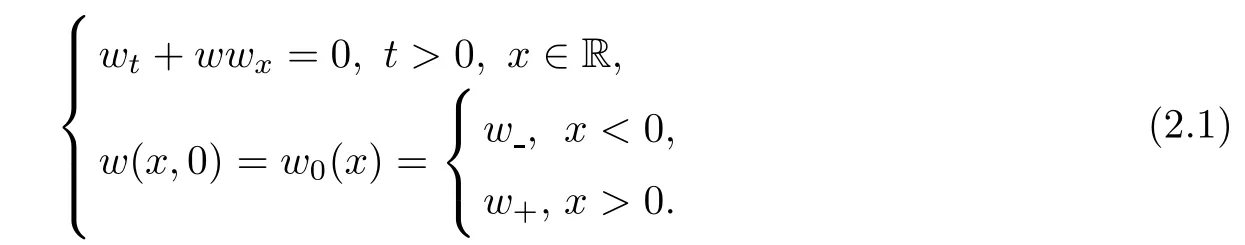

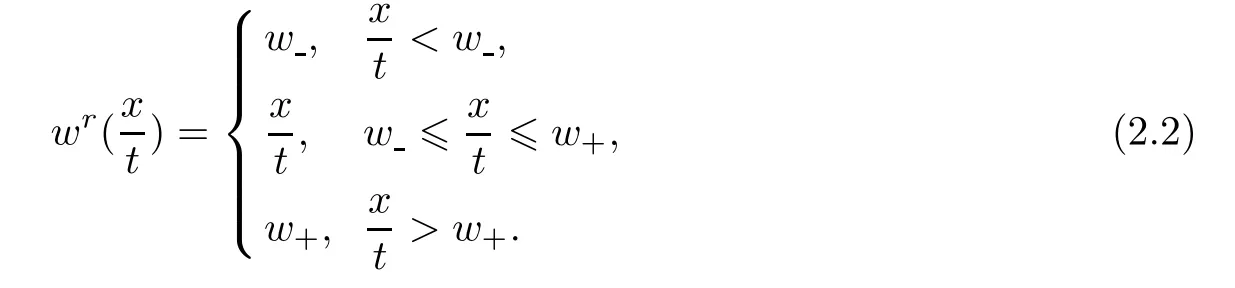
As in[16],the approximate rarefaction wave w(x,t)to(1.6)can be constructed by the solution of the Burgers’equation
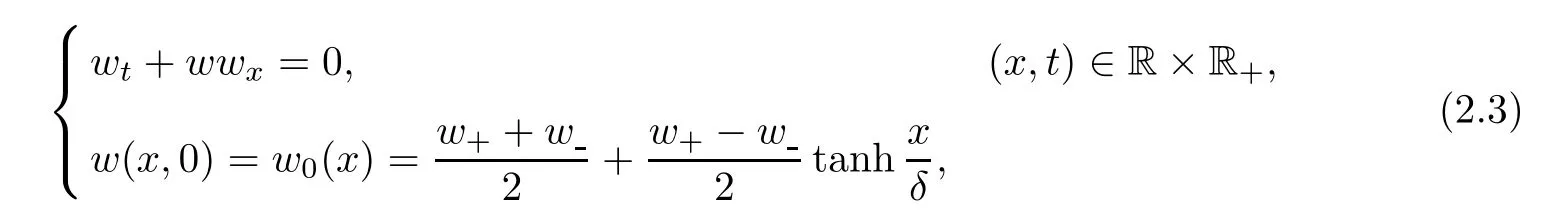
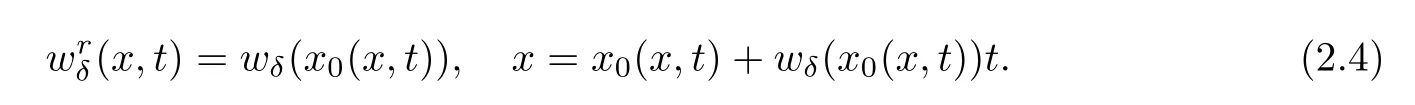
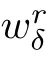
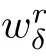
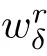
(2)The following estimates hold for all t>0,δ>0 and p∈[1,+∞]:
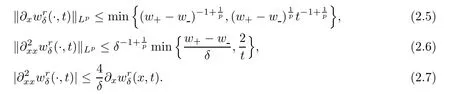
(3)There exists a constant δ∈(0,1)such that δ∈(0,δ],t>0,

From now on,we describe the rarefaction waves for the Euler equations(1.9).Assuming that the constant states(u,v)are fixed,(u,v)lies on the 1-rarefaction wave curve through(u,v).Setting w=λ(v)and w=λ(v)in(2.1)–(2.3),one can check that the unique solution(u,v)(x,t)to the Riemann problem(1.9)and(1.13)is given by
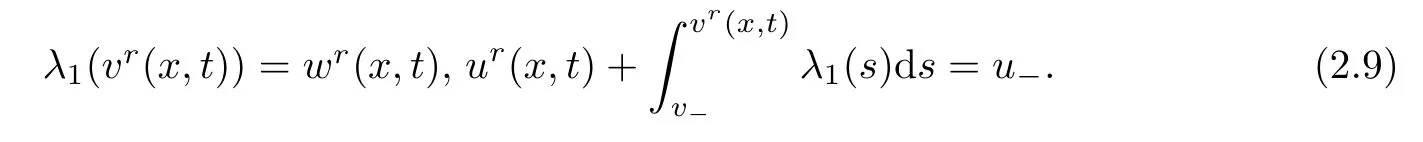

3 Proof of Theorem 1.1
In order to prove Theorem 1.1,we introduce the perturbation around the smooth rarefaction wave

and the scaled variables
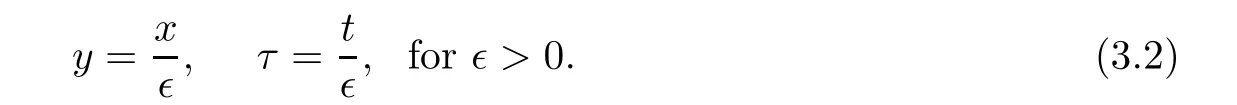
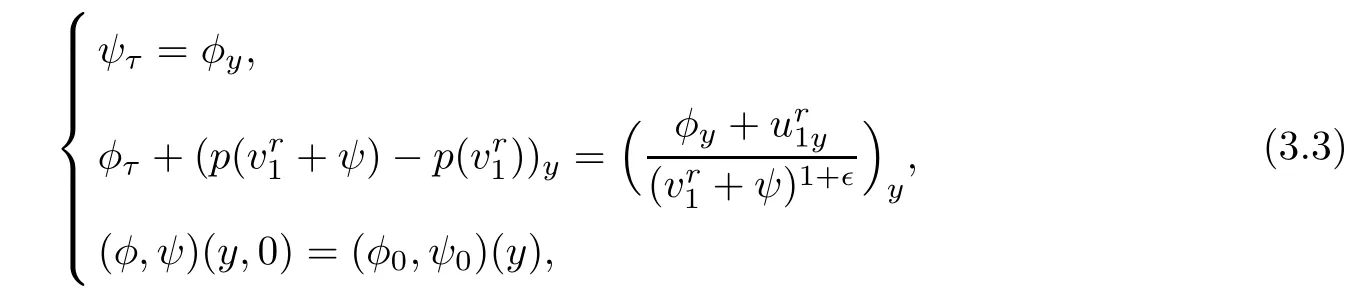
where(φ,ψ)(y)and its derivatives are sufficiently smooth away from y=0 but up to y=0 and
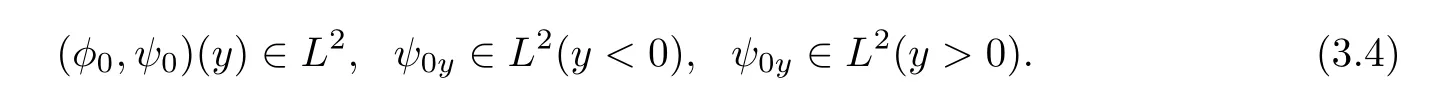
Proposition 3.1
Suppose that there exists a positive constant ηsuch that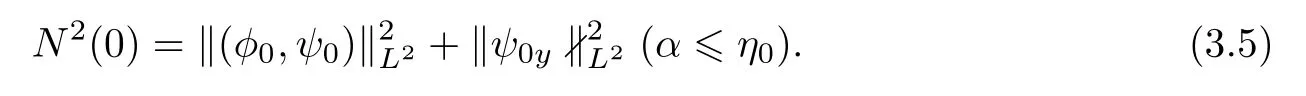
Then the Cauchy problem(3.3)–(3.4)has a unique global solution(ψ,φ)(y,τ)satisfying the following statements:
(1)The regularity assertions for(ψ,φ)(y,τ)are the same as those for(v,u)(x,t)of Theorem 1.1.
(2)There exists a positive constant C such that

(3)For any τ>0,there exists a constant c(τ)>0 such that
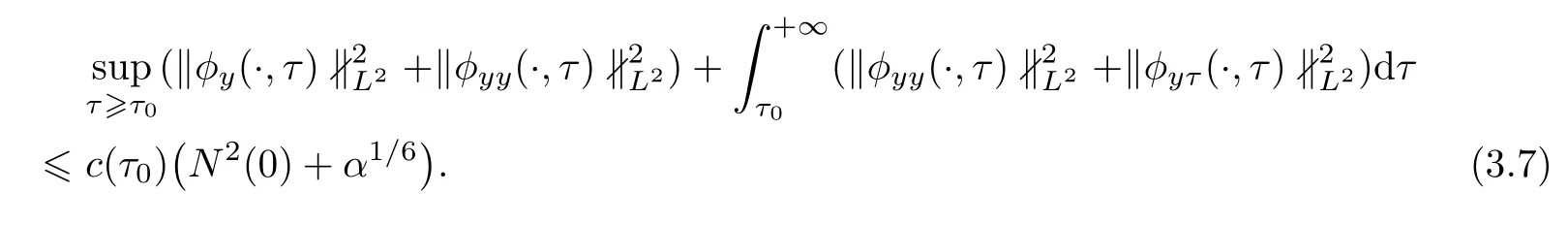
Theorem 1.1 follows directly from Proposition 3.1.As for the proof of Proposition 3.1,with the corresponding local existence theory stated in the Appendix to hand,it is sufficient to obtain the following a priori estimates:
Lemma 3.2
Let the assumptions in Proposition 3.1 hold.Suppose that the Cauchy problem(3.3)–(3.4)has a solution(ψ,φ)(y,τ)on R×[0,τ]for some τwith regularity as asserted in the local existence theory in Appendix.Set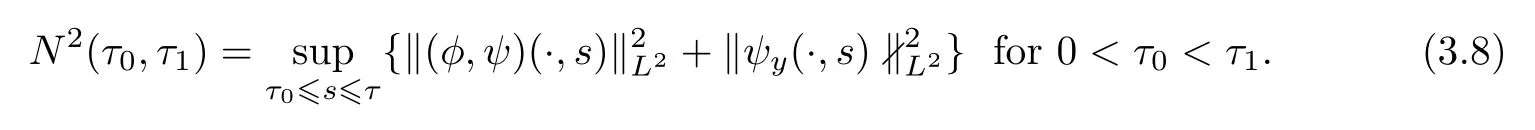
Then there exist positive constants η(≤η)and c independent of τsuch that,for each fixed τ>0,if

by Sobolev’s inequality.
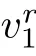







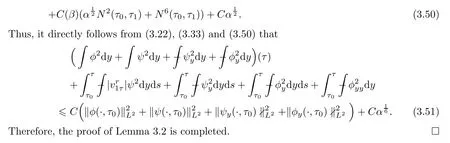
4 Proof of Theorem 1.2

where(u,v)(x,t)is assumed to be the solution to the problems(1.6)and(4.1).Substituting(4.2)and(4.3)into(1.6)and(4.1),one has that
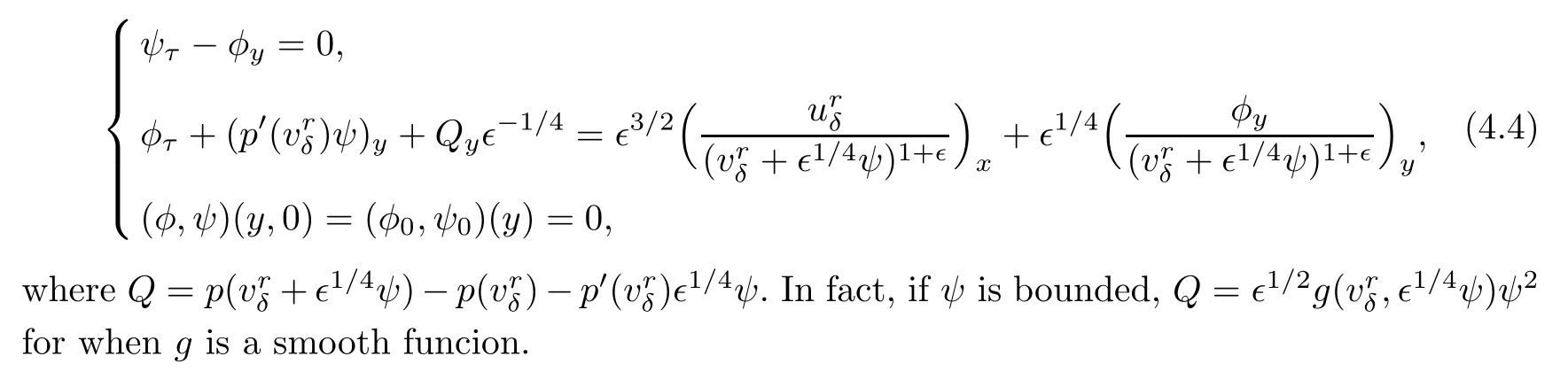
We seek a global-in-time solution(φ,ψ)to the reformulated problem(4.4).To this end,the solution space for(4.4)is de fined by

with 0<τ≤+∞.Then,we have the following result:
Proposition 4.1
There exist positive constants∊,δ,kand c which are independent of∊,or δ,such that for each∊∈(0,∊)and δ∈(0,δ),if
then the initial value problem(4.4)admits a unique global solution(φ,ψ)∈X(0,+∞)satisfying
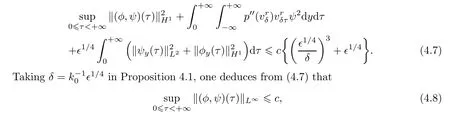
where c is a positive constant independent of∊.Moreover,a global smooth solution(u,v)(x,t)of(1.6)exists,satisfying(1.16)–(1.18)stated in Theorem 1.2 and
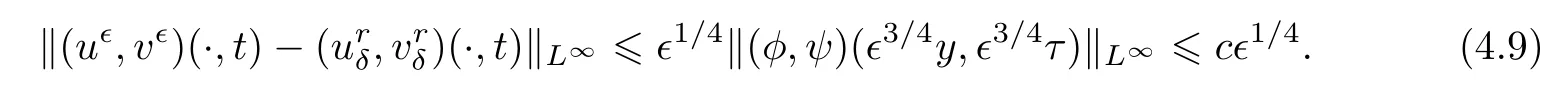
The inequality(2.12)in Lemma 2.2 implies that
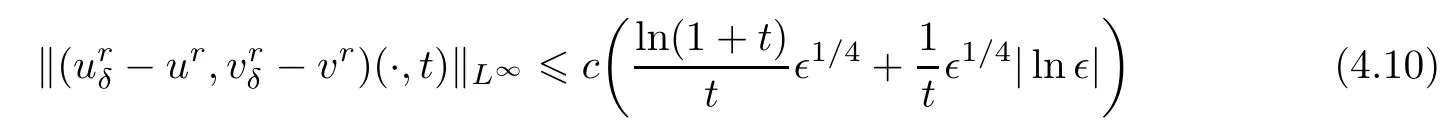
holds for all t>0.Thus,one can combine(4.9)and(4.10)to get the desired result of(1.19),and the proof of Theorem 1.2 is completed.
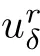
Proposition 4.2
(A priori estimate) Let(φ,ψ)∈X(0,τ)be a solution to the problem(4.4)for some τ>0.Then there exist positive constants∊,δ,k,and c,independent of∊,δ and τ,such that if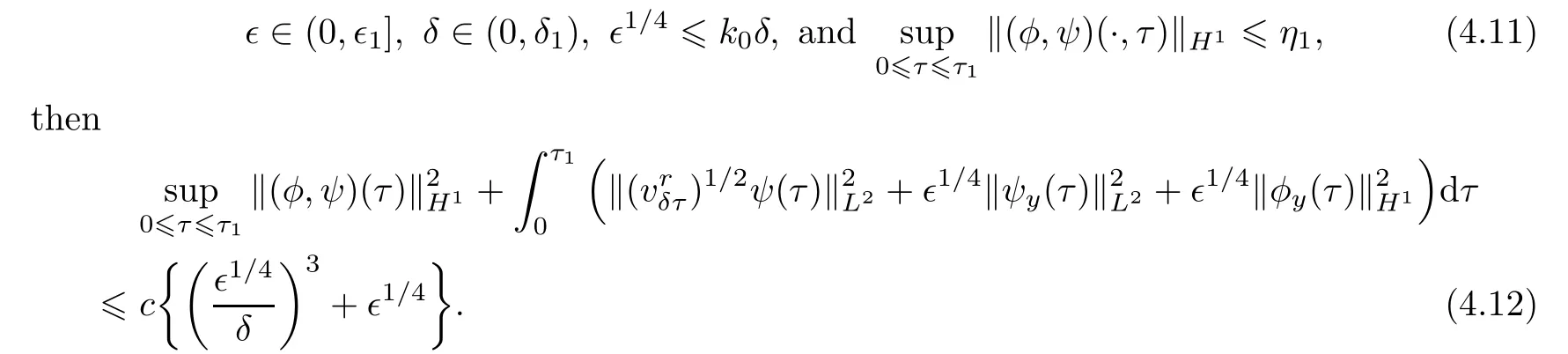
Based on the results in Lemma 2.2,we derive the a priori estimate(4.12)on two time levels,corresponding to 0≤t≤T≤1 and 1≤T≤t<+∞.This implies the framework for the rest of this section.In what follows,we always assume that a priori assumption(4.11)ensures that

Set

for τ<τ.
4.1 Finite time estimate
In this part,we study the behavior of(φ,ψ)(∊x,∊t)in the finite time interval 0≤t≤T≤1.

One can deduce from(4.20)and Lemma 2.2 that,for τ∈[0,τ],
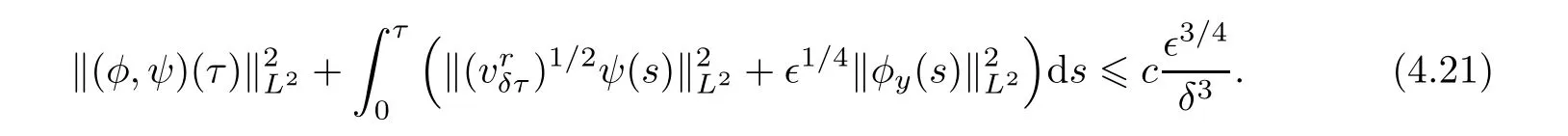
Step 2
Differentiating(4.4),multiplying by φ,and integrating the resulting equation over R,after integration by parts,we have that
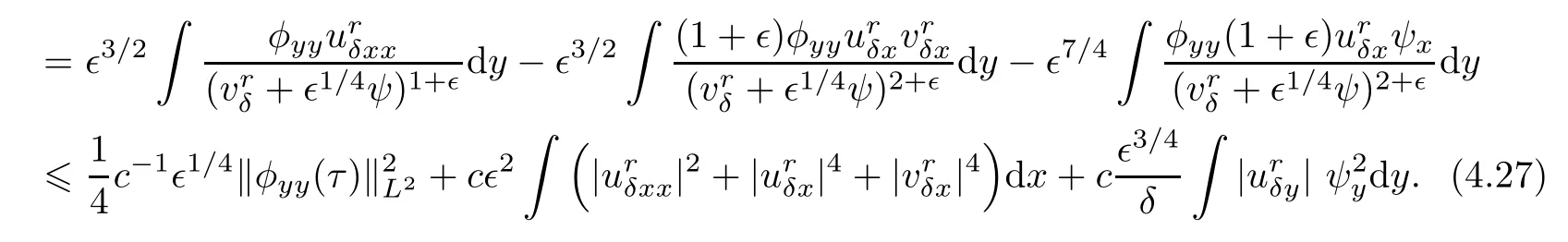
Thus,substituting(4.23)–(4.27)into(4.22)and integrating the resulting inequality with respect to τ,one has that
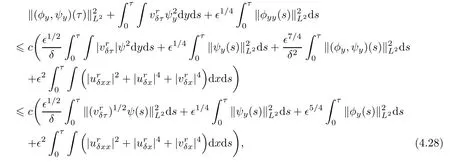
under the condition that∊/δ≤kby(4.11).
Step 3
Multiplying(4.4)by ψand integrating the resulting equation with respect to y,one has that
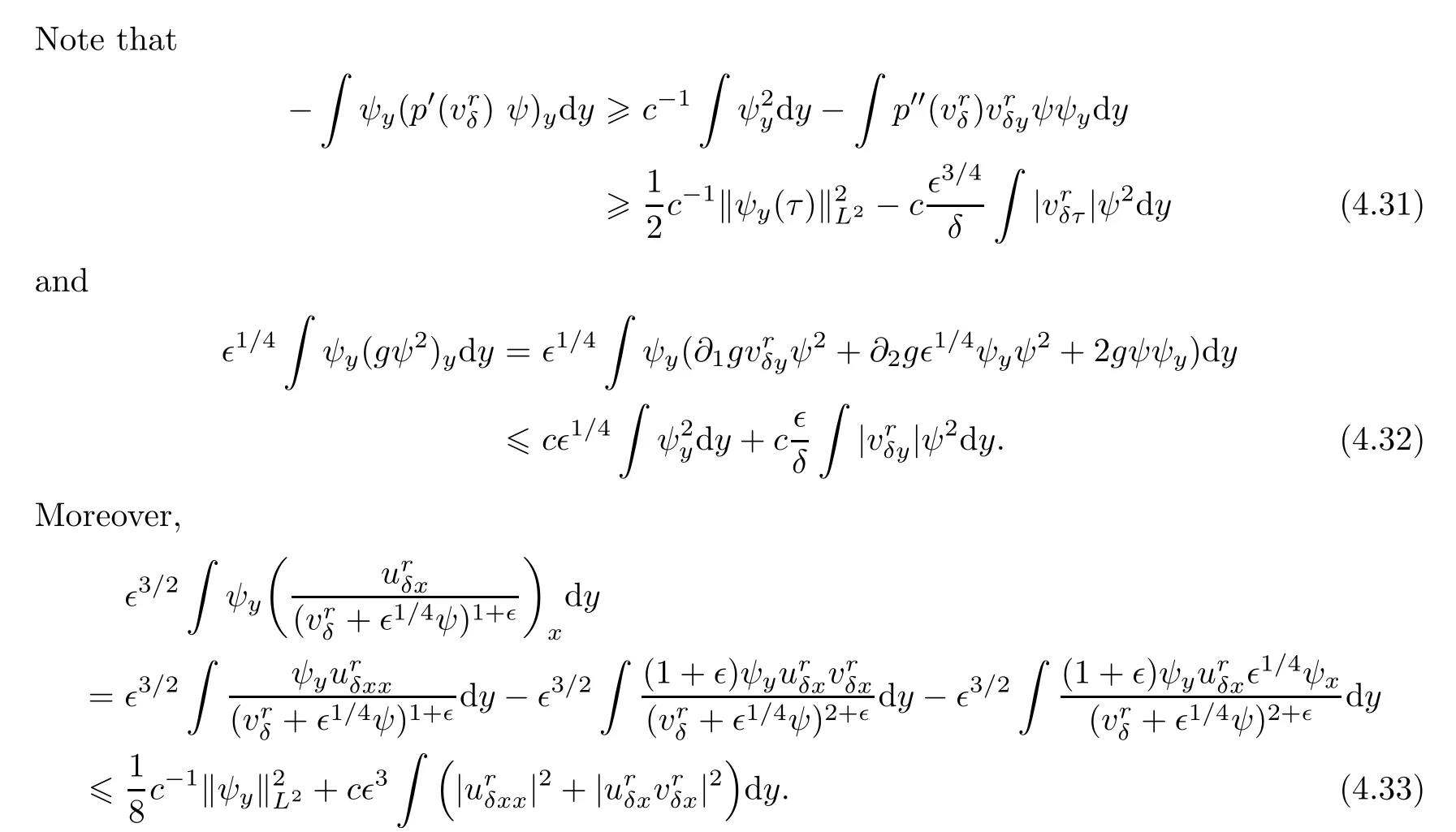
Inserting(4.30)–(4.33)into(4.29)and integrating the resulting inequality with respect to τ,one has that
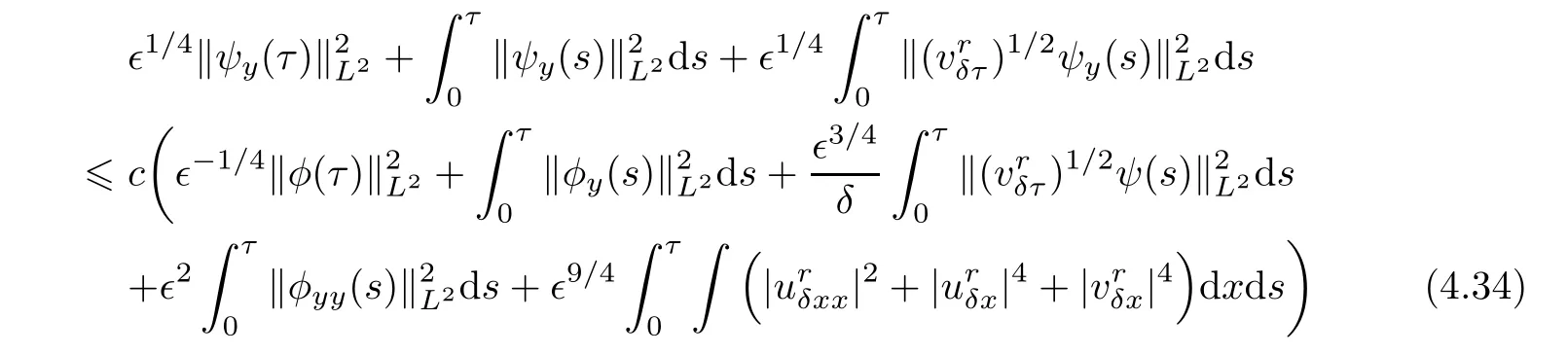
for τ∈[0,τ].
Step 4
Now,one combines(4.28)and(4.34)to get that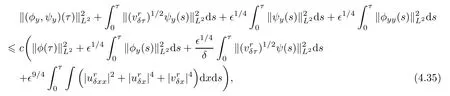
and the desired estimate(4.15)follows immediately.
4.2 Large time estimate
Now,we study the behavior of(φ,ψ)(∊x,∊t)for large time.In fact,one has the following result(once we have proved Lemma 4.4,Proposition 4.2 follows from Lemma 4.3 and Lemma 4.4 by taking T=T=1):
Lemma 4.4
Let Tbe in[1,+∞).Set τ=∊T,and suppose that τ≥τ.Then,for τ∈[τ,τ],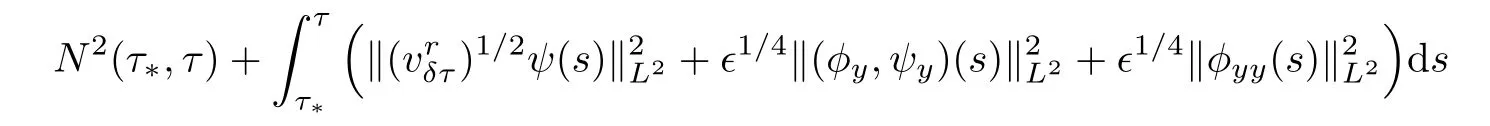

Proof
The right-hand term of(4.16)can be estimated as
With this bound,one can finish the proof by applying a similar argument as to that in[16];thus,we omit the details here.
Appendix
First,we give a heuristic description of the evolution in time of the jump discontinuity,which is crucial in corresponding energy estimates.It follows from the initial discontinuity and the Rankine-Hugoniot condition applied to(1.6)that
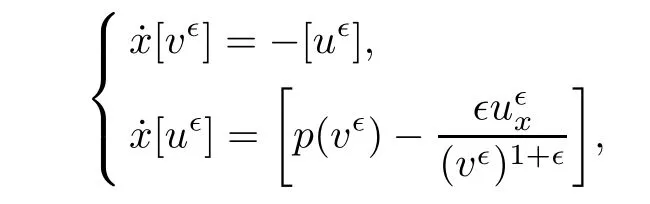
and then the jump condition

must hold.De fining
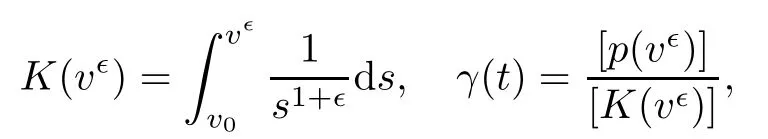
one can obtain that γ(t)is negative by(1.8)and

Then,the local(in time)existence and regularity results can be stated as follows(the proof is similar to[14,31]and omitted here):
Theorem A.5
For given(v,u)and(v,u)with v>0 and the initial data(v,u)satisfying 0
where α=|v−v|+|u−u|,and T and C depend only on(v,u),p(v),∊κ(v)and on upper bounds for α,E(0),F(0).Furthermore,if the solution exists up to any given time and satis fies

for some positive v and¯v,then the following statements hold:
(1)The regularity assertions in(1)of Theorem 1.1 hold with the additional assumption that vis separately H¨older continuous in the sets{x<0}and{x>0}.
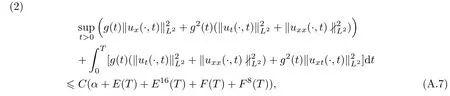

 Acta Mathematica Scientia(English Series)2021年5期
Acta Mathematica Scientia(English Series)2021年5期
- Acta Mathematica Scientia(English Series)的其它文章
- RIGIDITY RESULTS FOR SELF-SHRINKING SURFACES IN R4∗
- GLOBAL STRONG SOLUTION AND EXPONENTIAL DECAY OF 3D NONHOMOGENEOUS ASYMMETRIC FLUID EQUATIONS WITH VACUUM∗
- CONTINUOUS TIME MIXED STATE BRANCHING PROCESSES AND STOCHASTIC EQUATIONS∗
- SOME OSCILLATION CRITERIA FOR A CLASS OF HIGHER ORDER NONLINEAR DYNAMIC EQUATIONS WITH A DELAY ARGUMENT ON TIME SCALES∗
- COARSE ISOMETRIES BETWEEN FINITE DIMENSIONAL BANACH SPACES∗
- ZERO KINEMATIC VISCOSITY-MAGNETIC DIFFUSION LIMIT OF THE INCOMPRESSIBLE VISCOUS MAGNETOHYDRODYNAMIC EQUATIONS WITH NAVIER BOUNDARY CONDITIONS∗
