浮子阀型气液分离器的设计与研究

张 硕，张安妮

（1.西安石油大学，陕西 西安 710065；2.西安北方惠安化学工业有限公司，陕西 西安710302）

1 浮子阀型气液分离器的总体设计方案

1.1 结构设计

该系统由分离器外壳、浮子及其他零部件组成。浮子阀由筒体、阀芯、阀座组成，筒体顶部有气体加速口，下面排布有液体进口；阀芯由浮子筒、上下锥阀体、上下柔性导向杆、浮力调节子组成，上下锥阀体连接于浮子筒两侧，柔性导向杆采用万向节连接于锥阀体上，保证浮子筒可垂直运动；浮力调节子螺纹连接于浮子筒上，实现浮子阀的浮力可调；法兰将上、下阀座分别连接到筒体上下两端，阀座是与锥阀体相匹配的锥形孔[1-2]。系统结构图如图1所示，浮子阀结构图如图2所示。

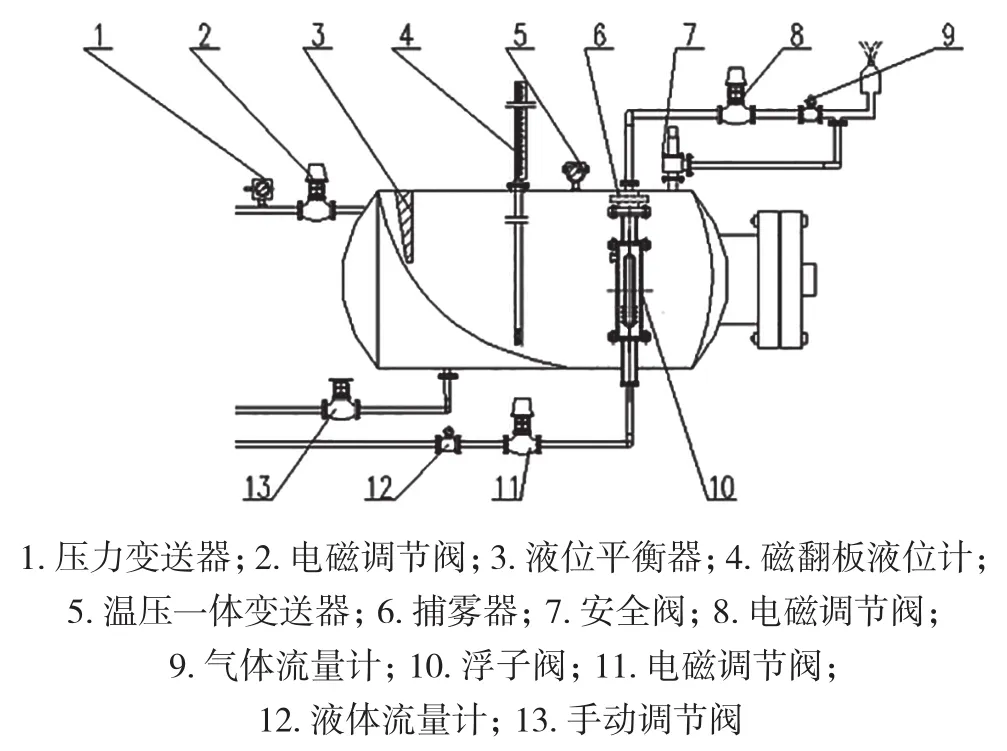
图1 浮子阀型气液分离器结构图

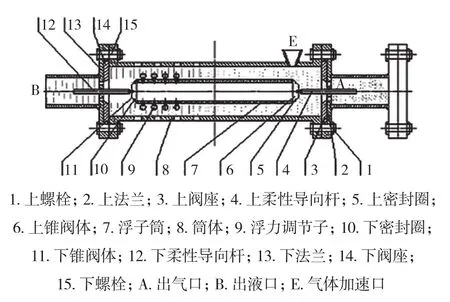
图2 浮子阀结构图

1.2 工作原理

气液两相流体在上部进入气液分离器后，对其进行初步分离，在气液分离器上部通过重力沉降后，进入浮子阀进行再次分离，分离器内的浮子阀悬浮在浮子筒内。分离后，气体上升穿过气体加速口进入筒体，经过捕雾器时，除去伴随的小液滴，最后从出气口出去。液体在下面经进液口再次回到筒体内，再从出液口流出。随着液体量不断减少，浮子筒被不断向下运动，通过柔性导向杆的作用，将下锥阀体压向下阀座的第二锥孔，当气体接近出液口时，出液口关闭，阻止气体从出液口流出。反之，随着液体量增多，液体界面上升，浮子筒上升，通过柔性导向杆的作用，将上锥阀体压向上阀座的第一锥孔，液体接近出气口时，出气口关闭，阻止液体从出气口流出，从而成功解决了出液口出气与出气口出液的问题。

2 浮子阀型气液分离器的结构设计

该系统设计的核心是浮子阀的结构设计。浮子阀由筒体、阀芯、阀座组成，通过法兰与外部管路连接[3]。具体结构参数包括：筒体内径d1、长度L1，浮子筒内径d2、长度L2，锥阀体锥度φ，柔性导向杆直径 d3、长度 L3，浮力调节子直径 d4、厚度 r。

利用伯努利方程对浮子阀内部混合流体的湍流流动问题进行分析。

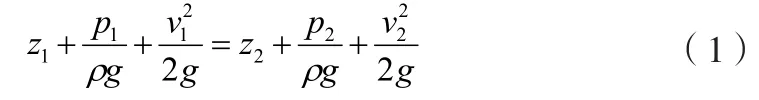
混合流体从进口流入，流动过程中浮子阀内的阀芯受到重力与浮力的作用，使得出气口和出液口的开启度随气液比的不同而发生变化。浮子的重力和浮力相等时，得到以下计算公式：

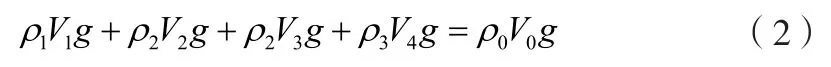
式中，ρ1为有机玻璃的密度值，1.18g·cm-3；V1为柔性导向杆总体积；ρ2为尼龙66的密度值，1.15g·cm-3；V2为锥阀体总体积；V3为浮子筒的体积；ρ3为聚甲醛POM塑料的密度值，1.42g·cm-3；V4为浮力调节子的总体积；ρ0为液体的密度值，1g·cm-3；V0为力平衡时液体漫过浮子筒的总体积。

由式(2)计算得到V0后，再计算筒内的液体到达浮子筒的高度，得到h=115.7mm，转换后，可得下方应有16个浮力调节子。

3 浮子阀型气液分离器的内部流场分析

采用FLUENT软件，对该新型气液分离器的内部流场进行仿真分析。将划分好的网格储存为MASH格式文件，然后导入到FLUENT软件，由于浮子阀内为两相流模型，选择欧拉模型和k-ε两方程模型，依次查看液相速度、气相速度和体积分数等的分布情况[4-5]。

在模拟过程中，进出口的边界条件依据实际工况条件得出的参数确定。该分离器的进口设定为速度入口边界，出口设定为压力出口边界，分别表示为Velocity-inlet和 Pressure-outlet。

在进行仿真计算时，将残差数量级定为万分之一，迭代的次数设置为2000次。观察残差曲线的整体趋势将要达到水平时，则计算接近收敛，流场的计算也就相对稳定，流场内部的各项参数基本不会发生变化，就可以停止仿真计算。下面对该新型气液分离器中的浮子阀部分进行模拟分析，得到内部阀芯在运动过程中，浮子阀内气液两相的体积和压力的分布情况，以及内部速度场的变化情况。

3.1 含气量占80%的两相流体的流场数值模拟分析

当浮子阀在出液口上方20mm时，由计算可知，此时两相流体中气体的含量占80%。图3和图4是浮子阀在出液口上方20mm时，两相液体的体积分布情况；图5~图7分别是浮子阀在出液口上方20mm时，z=0时截面两相液体的压力和体积分布情况；图8和图9是浮子阀在出液口上方20mm时，出气口位置处的气液两相的体积分布情况；图10和图11是浮子阀在出液口上方20mm时，出液口位置处气液两相的体积分布情况。

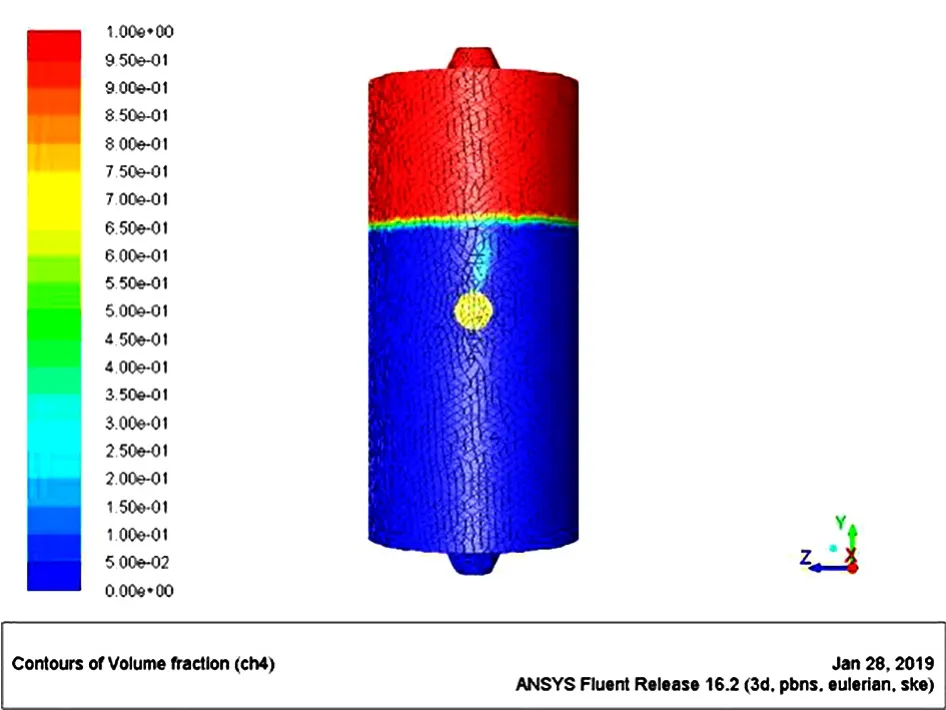
图3 气相体积分布云图

图4 水相体积分布云图

图5 水相体积分布云图

图7 混合流体压力分布图

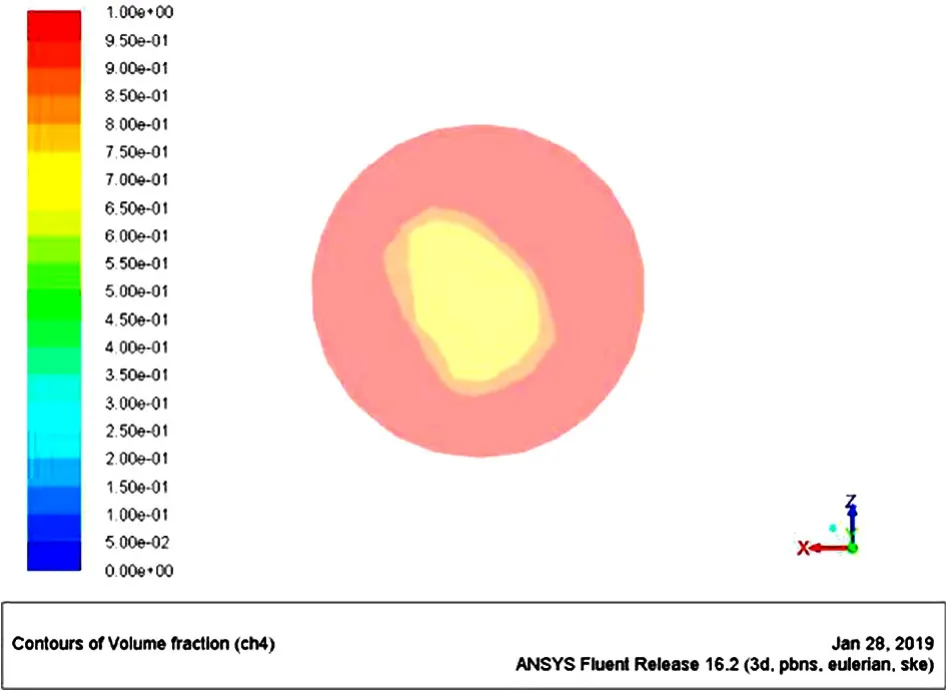
图8 出气口气体体积

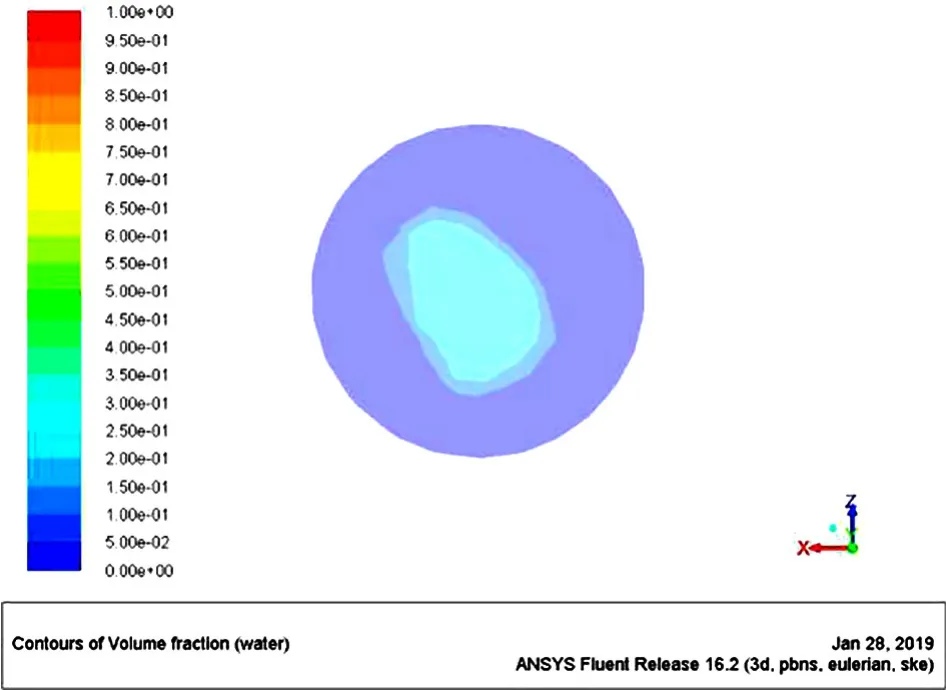
图9 出气口液体体积

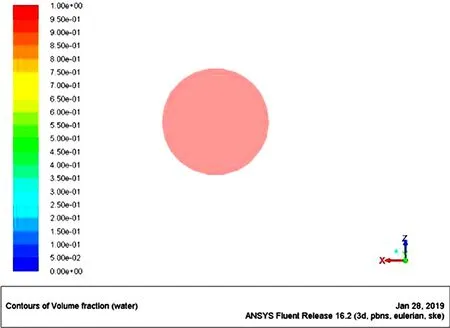
图10 出液口液体体积

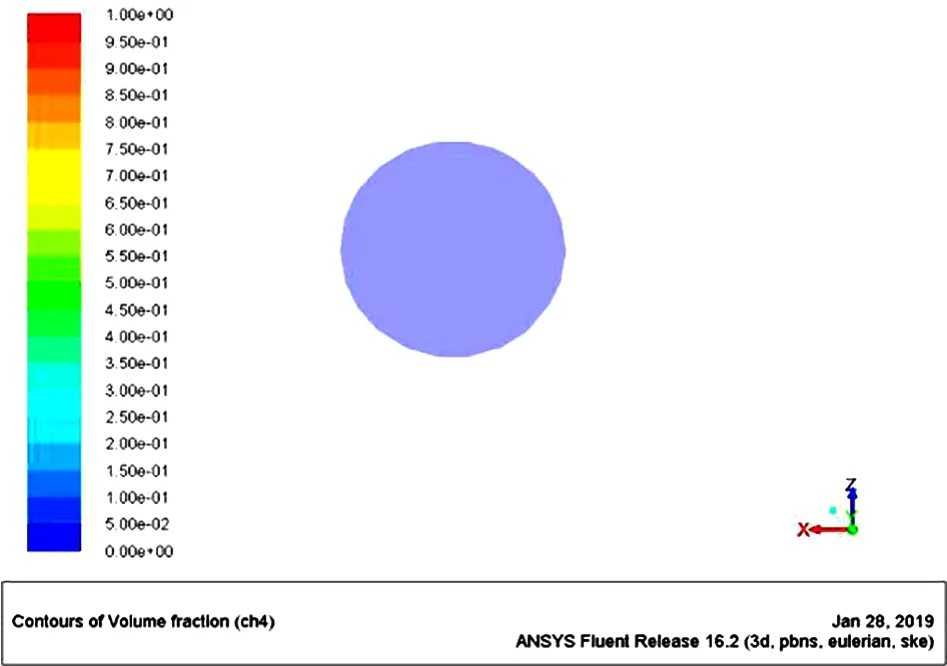
图11 出液口气体体积

观察图3~图6可知，当两相流体中的气体含量占80%时，浮子阀在出液口上方20mm位置处，气液两相有十分明显的分层现象，气体在上层分布，液体分布在下面。

图6 气相体积分布云图

由图7可以观察到，在出气口和出液口两个位置处，混合流体所受到的压力较大。由此，将对出气口与出液口位置处的体积云图作进一步分析。

由图8、图9可以看出在出气口位置处，气液两相流体的体积分布情况。贴近出气口内壁位置气相所占最多，约为0.8~1，在中心位置的气相所占分数最低，约为0.7~0.75。在出气口位置液相的分布情况刚好与气相相反。

由图10、图11可以看出在出液口位置处气液两相的体积分布情况。水相在出液口底部所占比例最高，约为0.89~1，在出液口位置气相的分布情况，刚好与液相相反，约占0~0.11。

从图3~图11可知，进入浮子筒的气液两相流体，当阀芯重力大于液体的浮力时，阀芯不断向下直到阀门关闭。浮子阀在出液口上方20mm位置处，水相从出液口流出，气相被阻挡，不能从出液口流出，避免出液口出气。可以看出此结构对气体含量大的两相流体能够实现较好的分离。

3.2 含气量占50%两相流体的流场数值模拟分析

当浮子阀在出气口下方20mm时，由计算可知，此时两相流体中气体的含量占50%。图12和图13是浮子阀在出气口下方20mm时，两相液体的体积分布情况；图14~图16是浮子阀在出气口下方20mm时，z=0截面两相流体的压力和体积分布情况；图17和图18是浮子阀在出气口下方20mm时，出液口位置处的气液两相的体积分布情况；图19和图20是浮子阀在出气口下方20mm时，出气口处气液两相的体积分布情况。

图12 三维气相体积分布云图

图13 三维水相体积分布云图

图14 气相体积分布云图

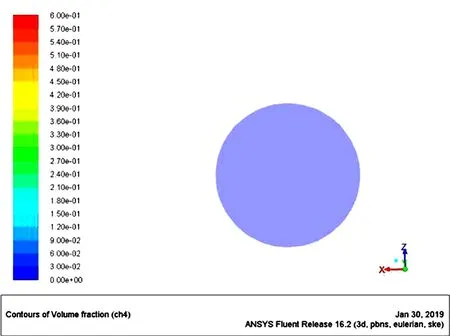
图17 出液口气相体积

图18 出液口水相体积

观察图12~图15可知，两相流体中的气体含量占50%时，浮子阀在出气口下方20mm位置处，气液两相有十分明显的分层现象，气体在上层分布，液体分布在下面。

由图16可以观察到，由于阀芯距离出气口较近，出气口所受压力较大，因此对出气口与出液口位置处的体积云图作进一步分析。

图16 混合流体压力分布图

由图17、图18可以看出在出液口位置处，气液两相流体的体积分布情况，水相体积分数为0.80~1，气相所占较少，约为0~0.11。

由图19、图20可以看出在出气口位置处的气液两相体积分数，气相体积分数约为0.80~1，水相约为0~0.11。

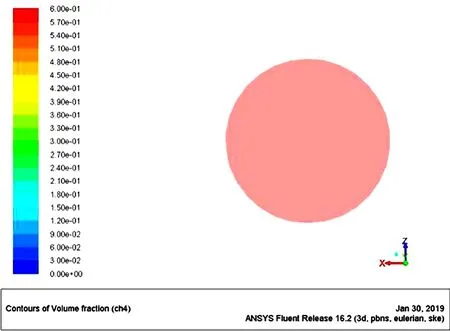
图19 出气口气相体积

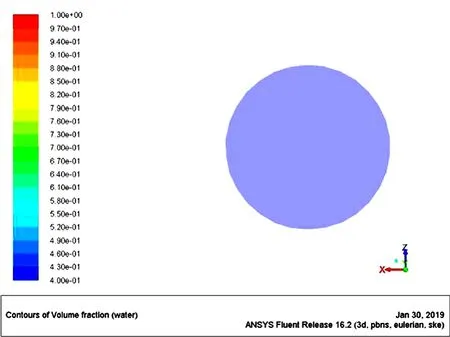
图20 出气口水相体积

进入浮子筒后的气液两相流体，当阀芯重力等于液体的浮力时，阀芯不断向上直到阀门关闭。浮子阀在出气口下方20mm位置处，气相从出气口跑出，液相被阻挡，不能从出气口出去，避免出气口出液。可以看出此结构对液体含量大的两相流体能够实现较好的分离。

3.3 浮子阀内的速度场研究

气液分离器内部流体的流速对分离效果的影响很大。如果进口速度较大，将会导致两相流体在分离器内停留的时间缩短，那么气液分离就不彻底，导致液体掺杂着气体一起流出。设置该模型中两相流体在浮子阀处的入口速度为0.3m·s-1，对浮子阀内的速度进行模拟分析，同样选取z=0截面、出气口及出液口这3个位置处进行研究，结果如图21~图23所示。

由图21可以看出，在出液口贴近内壁处，流体的流速偏大，约为1.6m·s-1。由图22可以看出，在出气口内壁处几乎没有流体经过，而在中心位置处的流速较大，约为1.3m·s-1。由图23可以看出，阀芯上部的速度比下部快，上部速度约为1.67m·s-1。

图21 出液口流体速度

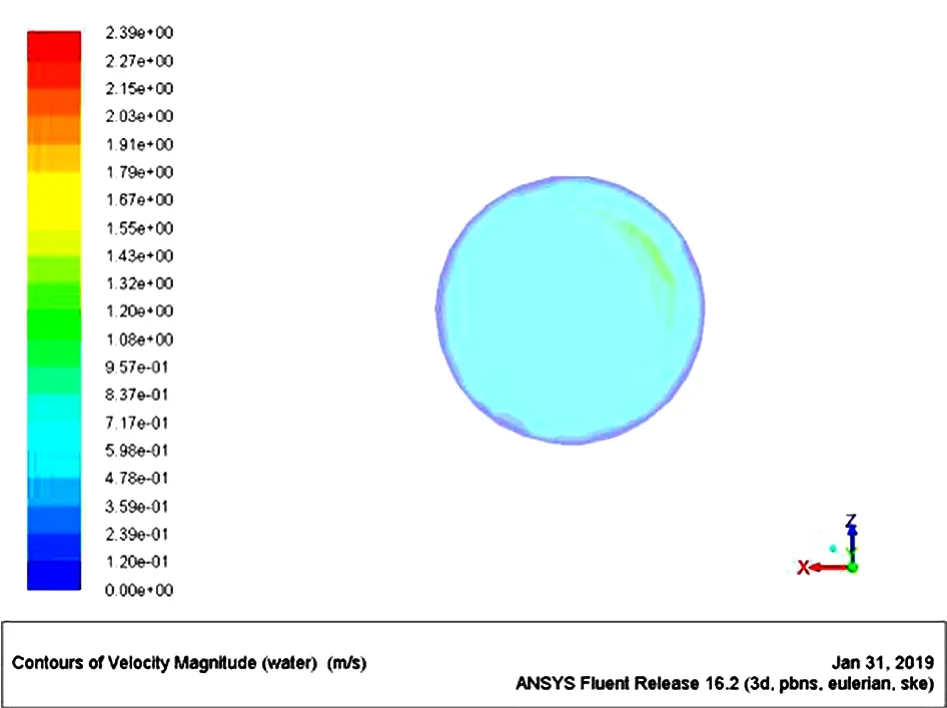
图22 出气口流体速度

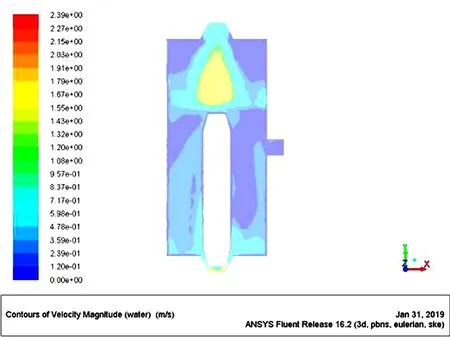
图23 z=0截面的速度云图

通过对内部速度场的模拟，可知在浮子阀结构中，阀芯所在位置附近的流体速度较快，但在出气口、出液口和容器上端壁面附近位置的流体速度都很慢。分析可知，该浮子阀内的两相流体有充足的停留时间，可达到分离条件，实现更好分离。

4 结论

本文针对设计的浮子阀型气液分离器进行研究，依据伯努利方程，建立了新型气液分离器相关结构参数的数学模型，并构建了三维模型。利用FLUENT软件对其内部流场进行了分析，验证了浮子阀型气液分离器可以基本解决“出气口出液，出液口出气”的实际工程难题。同时，流体在浮子阀内有充分的停留时间进行分离，能够更好地满足分离要求。