面向积水推测的机会式感知轨迹选择

张伟杰，於志勇，黄昉菀，朱伟平

(福州大学 数学与计算机科学学院 福建 福州 350108)

0 引言

随着感知技术和计算环境的成熟，大数据的应用领域越来越广泛，城市计算[1]就是运用这类数据来解决城市中的各类问题，促进智慧城市[2]的发展。城市积水影响着城市居民的日常出行，阻碍了灾害天气下城市的正常运作。近年来，虽然政府加强城市排水系统的建设与优化[3-4]，但是由于城市环境极其复杂，城市积水问题在全国各个城市尚未解决。城市积水如果未被及时发现并处理，就有可能损害城市排水系统，导致城市内涝甚至发生城市洪涝灾害。因此，为了保障城市居民的日常出行不受影响，和维护灾害天气下城市的正常运作，及时发现城市何处积水尤为关键。

以往的城市积水监测多是通过摄像头观测、人为反馈等方式，这种方式耗时耗力、覆盖范围小，且在灾害天气下风险性较高，又容易失效。但随着传感器、无线通讯技术的发展以及移动设备的普及，出现了一种新型的数据采集模型——群智感知[5]，可通过大量移动节点来收集数据并上传，在感知平台分析后得到大范围的城市数据。群智感知因其成本低、部署灵活等优势，在空气质量推测[6-7]、公共事件信息收集[7]等方面有了重要应用。但是在现实应用过程中，由于移动节点时空分布不均、设备故障等原因，移动节点可能会无法正常上传数据，导致一些区域无法准确收集到信息。因此，如何通过已感知到的数据来推测出缺失的数据，是一个有价值且需要深入探讨的问题。

目前城市积水问题的相关研究大多是基于灾害天气下进行的，而缺少针对非灾害天气下的城市积水推测。然而，非灾害天气下的城市积水推测与灾害性天气下的城市积水推测有较大差异。本文基于深圳市真实积水数据在不同天气情况下的分析，并且考虑到目前城市都已经具备一定的排涝能力，且在非灾害天气下降雨量较低、日晒促使城市积水自然蒸发等因素，认为非灾害天气下城市积水的发生概率较低，可视为异常事件处理。而在灾害天气下，城市积水发生概率较高。

为了研究非灾害性天气下的积水推测问题，本文考虑了降雨以及历史积水状态，对积水监测站点的积水状态进行推测，同时为了进一步提高积水推测的准确度，引入了启发式策略选择公交车轨迹。本文的主要工作可以概括为：

1)阐述了在非灾害天气下的城市积水推测问题，并提出了一种结合选择感知轨迹来实现城市积水推测的方式；

2)通过历史积水数据，根据滑动雨量以及历史积水状态，采用孤立森林方法推测城市各个积水监测站点的积水状态；

3)采用了两种轨迹选择方式：随机选择和贪心选择。在贪心选择中，本文优先选择经过剩余积水监测站点数量最多的轨迹。为了进一步提升推测精度，根据轨迹得到的真实记录对孤立森林的推测结果进行修正。并在选择轨迹后，根据轨迹得到的真实记录使用压缩感知实现积水推测；

4)为了验证本文提出算法的有效性，采用了深圳市水务局积涝点水位数据、深圳市滑动雨量数据、深圳市公交线路轨迹数据进行验证。实验结果表明：与孤立森林算法来推测城市各处积水状态相比，结合群智感知思想，选取公交车感知轨迹生成感知数据的方法能进一步提升推测准确度。

1 相关工作

随着更多的城市积水相关数据被采集利用，城市积水问题的研究也越来越丰富。徐艺扬等[8]基于历史数据及GIS空间分析，综合研究了上海市的降雨、城市建设用地扩张、人口集聚分布、城市数字高程、基础设施排水能力等因素对中心城区暴雨内涝发生的影响。Chen等[9]提出了一种低成本、实时的雷达方法，利用大规模的车辆轨迹数据和异构的道路环境感知数据来识别涵盖了城市积水的道路障碍物。王慧军等[10]提出了一种基于城市区域网格划分的暴雨积水预警模型，采用了一种非结构化的网格划分方法来建立城市积水预警模型。魏军等[11]利用石家庄市高精度城市地理信息等基础数据，将城市河网、路网、管网和社区的计算网格分层划分，形成分区、分层和立体多重的内涝计算模式,构建了石家庄市暴雨内涝数学模型。

近年来孤立森林在异常监测领域应用广泛，Yao等[12]基于孤立森林的思想提出了一种新的异常检测算法dForest(分布森林)。该方法将孤立森林中随机生成的子树改进为建立一组特殊的二叉树，称为分发树。Puggini等[13]将孤立森林结合一种降维变量选择方法应用于检测发射光谱数据的异常检测系统。Hou等[14]结合了Hadoop分布式存储系统与孤立森林，将检测模型构建和异常评价过程并行化，提高了检测效率，扩大了应用范围。

2 问题定义

为了更好地定义面向积水推测的机会式感知轨迹选择问题，本文预先定义了一些符号。位置集合P={p1,p2,…,pk}，其中pk代表第k个网格的位置。时间集合D={d1,d2,…,di}，H={h1,h2,…,hj,…,h24}，dihj表示第i天的第j小时。公交车集合C={c1,c2,…,cq}，公交车线路轨迹集合M={m1,m2,…,mq}，mq为公交车q的轨迹，是由若干个位置组成的集合，mq⊆P。所选公交车感知到的若干个位置的积水数据Z={z1,z2,…,zq}。

每小时各个位置都存在三种数据状态：感知结果为1，有积水；感知结果为0，无积水；感知结果为-1，即未被感知。公交车每小时都经过若干个位置，即公交车轨迹，下一小时也按相同顺序经过同样的位置。不同的公交车的轨迹不一样，位置序列的长度也可能不一样。同一辆公交车在不同小时的轨迹是一样的。公交车在每小时开始发车时，决定是否开启其感知设备参与感知任务。如果开启，则该公交车该小时内经过的每一个有积水监测站点的位置都被感知，返回结果1或0。如果未打开，则即使经过，位置仍然未被感知。本文实验基于以下假设进行：各积水监测站点的积水状态在一小时内不会改变；公交车一小时内能经过该公交车线路上的所有位置；若公交车开启感知设备，则只要经过积水监测站点，所在网格就能采集到该积水监测站点的积水状态。由于F1score同时兼顾了分类模型的精确率和召回率，是模型精确率和召回率的调和平均，且最大值为1，最小值为0，因此本文采用F1score作为模型性能的度量。

F1score=2·(precision·recall)/(precision+recall)。

问题：在dihj开始时，给定公交车集合C，公交车线路轨迹集合M，在一定预算下选取N辆公交车来参与感知任务，得到感知数据Z，目标是在dihj结束时，根据dihj数据及历史数据推测dihj所有未被感知位置的积水状态，并根据感知数据Z提升推测准确度。

3 方法

3.1 积水推测

本文采用了孤立森林算法和压缩感知作为推测积水的方法。孤立森林多应用于连续数据的无监督异常检测，与其他异常检测算法不同的是，孤立森林将异常点孤立出来而不是描写刻画正常点。孤立森林由多棵孤立树构成，孤立树是一种随机二叉树，且孤立树除了叶子节点外的所有节点都是有两个孩子的内部节点[15]。孤立树由以下算法构成。

算法1iTree(U,e,l)。

输入：U为输入数据，e为树当前高度，l为树限制高度。

输出：一棵孤立树。

步骤1 从U中随机选取一个子集u′作为构建孤立树的训练集。

步骤2 在所有特征中选取一个特征作为孤立树的根节点，再从该特征的取值范围中随机选取一个值。

步骤3 根据选出的值对u′中的所有数据进行分类，将小于该值的数据放入左子节点，大于等于该值的数据放入右子节点。

步骤4 递归执行步骤2、3，直到构成的节点都为叶子节点或者达到限制的树深度，又或者节点上所有数据的特征值都是相等的。

步骤5 返回构建的孤立树。

孤立树检测异常的依据为：异常的样本需要被划分的次数较正常样本来说比较少，即异常样本能够更快地被划分到叶子节点，路径较短；特征具有可区别(如极值)的样本在分割过程中更容易被划分。

在构建完t棵孤立树后，让每个样本点xi遍历所有孤立树，可以计算得到在森林中的平均高度h(xi)，对所有样本点的平均高度进行归一化处理。异常值分数s的计算公式为

s(x,k)=2-E(h(x))/c(k)，c(k)=2H(k-1)-2(k-1)/k。

其中：E(h(x))是孤立森林的路径长度h(x)的均值；H(k)=lnk+γ，γ是欧拉常数。

可以看出当E(h(x))趋近于0时，异常分数s越趋近于1，则样本被判定为异常。当E(h(x))趋近于n-1时，异常分数s越趋近于0，则样本被判定为正常。

非灾害天气下的城市积水问题可视为异常检测问题进行处理，本文通过构建积水监测站点的滑动雨量、dihj-1时刻的积水状态、dihj-2至dihj-24各个时刻的积水状态这25个特征。将148个积水监测站点，在dihj时刻之前的积水数据作为训练集训练孤立森林，将dihj时刻所有站点的积水数据作为测试集，推测结果由孤立森林给出的异常值分数来确定。本文分别尝试选择1至10条轨迹，将对应生成的感知数据加入训练集，但是模型的效果相较于未加入感知数据的模型更差，所以最终未将感知数据加入训练集。

3.2 压缩感知

压缩感知[16]在恢复稀疏的时空数据中具有广泛的应用。根据对2019年深圳市真实积水数据的分析，91.2%记录的积水状态为无积水，且存在部分时刻所有站点的积水状态与相邻时刻相同，因此依据积水数据构建出的真实矩阵可视为低秩矩阵，可通过压缩感知进行压缩和重构。但也由于非灾害天气下的城市积水发生较少，可能出现感知到的位置积水状态都为无积水，即收集矩阵为零矩阵，在这种情况下压缩感知效果会比较差。压缩感知的具体步骤如下。

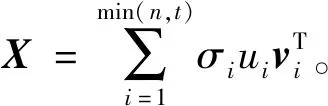
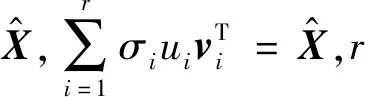
进一步可以转化为

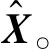
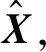
算法2Greedy(W,N)。

输入：W为各轨迹经过含积水监测站点的网格编号集，N为选择的轨迹条数。

输出：选择的轨迹集T。

步骤1 初始化各轨迹经过含积水监测站点的网格数量集K，W包含Len条轨迹。

步骤2 找到经过含积水监测站点的网格数量最多的轨迹t。

步骤3 将该条轨迹加入T。

步骤4 删除集合W中包含轨迹t经过的网格；更新K。

步骤5 循环执行步骤2～4N次，返回选择的轨迹集T。

3.3 轨迹选择

考虑到选择公交轨迹参与感知任务生成感知数据需要花费成本，因此在一定成本的限制下，为了提升选择的轨迹对积水推测的效果，本文希望选择的轨迹能够覆盖更多的积水监测站点，以提供更充足的真实数据，结合孤立森林算法、压缩感知算法，提升积水推测的准确度。在感知轨迹选择阶段，本文采用了随机选择和贪心选择两种方式。具体来说，在数据预处理阶段，我们将公交线路轨迹及积水监测站点等数据都映射至网格，并算出各条轨迹经过的积水监测站点的数量；在通过贪心选择算法选择感知轨迹时，本文优先选择经过含积水监测站点的网格数量最多的轨迹。

4 实验

4.1 数据集描述

本文实验数据来自深圳市政府数据开放平台及深圳市气象局。深圳市水务局积涝点水位原始数据字段包含水位编号、测站编码、时间、水位；深圳市水务局积涝点水位数据共1 332 577条记录，时间为2019年1月1日06:00到2020年2月22日16:00。深圳市水务局积涝点测站数据原始数据字段包含测站编码、测站名称、站点经度、站点维度；深圳市水务局积涝点测站数据共有170条记录，即有170个积水监测站点，站点的经纬度区间分别为[113.778 554,114.578 076]、[22.477 575,22.806 801]。深圳市公交线路轨迹数据原始数据字段包含记录编号、创建时间、修改时间、纬度、轨迹编号、经度、组成顺序；深圳市公交线路轨迹数据共有3 634条轨迹，4 057 364条记录。由于深圳市滑动雨量数据为手动爬取，该数据集由时间为行、滑动雨量监测站点ID为列的矩阵构成。深圳市滑动雨量监测站点数据字段包含站点编号、站点名称、区域编号、区域名称、站点经度、站点纬度、站点高度、站点地址；深圳市滑动雨量监测站点数据共205个降雨监测站点，共8 450条记录，经纬度区间分别为[113.767,115.129 021]、[22.4,22.97]。时间为2019年5月8日00:00到2020年5月31日23:00。

4.2 实验数据预处理

本文选取了时间区间为2019年5月8日00：00到2020年5月31日23：00的数据进行实验，并删除了该时间区间内18个无数据或数据缺失过多的积水监测站点数据。首先，由于深圳市水务局积涝点水位数据、深圳市滑动雨量数据都有一定程度的缺失，所以本文首先通过线性插值对数据集进行补全。线性插值通过一条穿过已知两点的直线来近似表示原函数，因此给定两点(xi,yi)，(xi+1,yi+1)，x在这两点之间，y(x)的计算公式为

y(x)=yi+((yi+1-yi)/(xi+1-xi))*(x-xi)，

在通过线性插值补全后，深圳市水务局积涝点水位数据、深圳市滑动雨量数据中所有站点在任意时隙dihj都有对应数据。其次，由于深圳市水务局积涝点水位数据中各站点的记录频率不定，且本文实验基于各积水监测站点的积水状态在一小时内不变的假设下实现。所以进行以下处理：以一小时作为一个时段，若站点在单个时段内有多条记录，则保留记录时间最晚的真实积水数值作为该时段的积水状态；若单个时段内只有一条记录，则该记录的积水数值为该时段的积水状态。如表1所示，由于5:00至6:00时段内有5:57、6:00时刻的记录，且两条记录都为真实值，所以仅保留6:00记录。6:00至7:00时段内有6:07、6:17、6:27、6:32、7:00这5条记录，且7:00时刻的记录值是线性插值得到的估计值，6:32时刻为该时段内记录时间最晚的真实记录，因此将6:32时刻的积水数值赋值给7:00时刻，然后删除7:00时刻以外的记录。7:00至8:00时段、8:00至9:00时段内都仅有一条记录，因此该条记录即为该时段的积水状态。接而，由于本文研究非灾害天气下的城市何处积水问题，所以将积水数据数值化为0、1，即0代表该站点的积水状态为无积水，1代表该站点的积水状态为有积水。

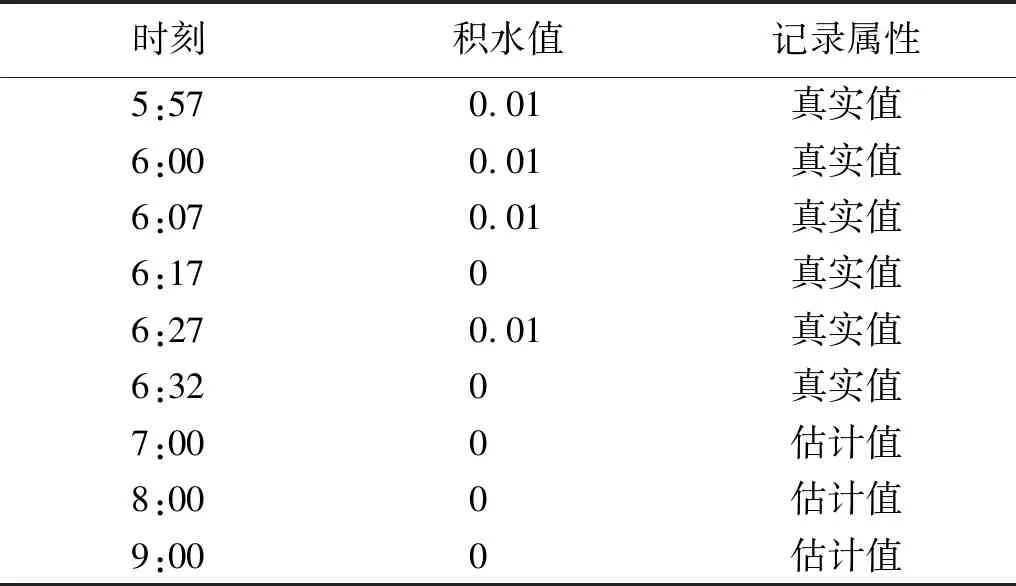
表1 2019年5月27日5时至9时积水监测站点48积水记录Table 1 Water accumulation records of 48 water accumulation monitoring sites from 5 to 9 on May 27,2019

同时，本文对经纬度分别在[113.778 554,114.578 076]、[22.477 575，22.806 801]的深圳市区域进行划分，将该区域划分为3 200个网格，每个网格大小为1 km *1 km。将积水监测站点根据经纬度映射至网格中。同一网格中有多个站点时，保留出现积水次数较多的站点。经过这一步的处理，共有148个网格中有积水监测站点被保留。接着，将滑动雨量监测站点根据经纬度映射至网格。当积水监测站点所在网格有滑动雨量监测站点时，将同网格滑动雨量监测站点的滑动雨量作为该积水监测站点的滑动雨量。对没有同网格滑动雨量监测站点与之匹配的积水监测站点，本文考虑到降雨的区域性，将与积水监测站点距离不超过3.5 km且相距最近的滑动雨量监测站点的滑动雨量作为该积水监测站点的滑动雨量。最后将由若干个经纬度点组成的公交线路轨迹也映射至网格。

4.3 实验结果及分析

4.3.1孤立森林 本文为了验证所提算法的有效性，分析了孤立森林、孤立森林结合随机选择、孤立森林结合贪心选择实现积水推测的实验结果。图1展示了三种方法的实验结果，其中横坐标为0处对应孤立森林实现积水推测，其余部分对应两种轨迹选择方式与孤立森林结合实现积水推测。从图1中箱形图部分可以看出，孤立森林实现推测的三种方式的所有结果的上四分位数、上限都为重合且数值为1.0；随着贪心选择轨迹条数的增多，下限逐步提高，异常点个数逐步减少，且异常点减少的个数明显优于随机选择；图1折线部分是对2019年5月9日至31日内每小时分别进行积水推测得到的F1score取均值的结果。从图1中折线部分可以得到，不论是结合随机选择或贪心选择实现积水推测的结果都优于单独使用孤立森林。随着选择轨迹条数的增多，推测的F1score也随之提高，且贪心选择对应的F1score的提升程度大于随机选择。综上所述，孤立森林结合随机选择、孤立森林结合贪心选择实现积水推测的效果优于单独使用孤立森林，且随着选择轨迹条数的增多，贪心选择相较于随机选择更能提升积水推测的准确度。

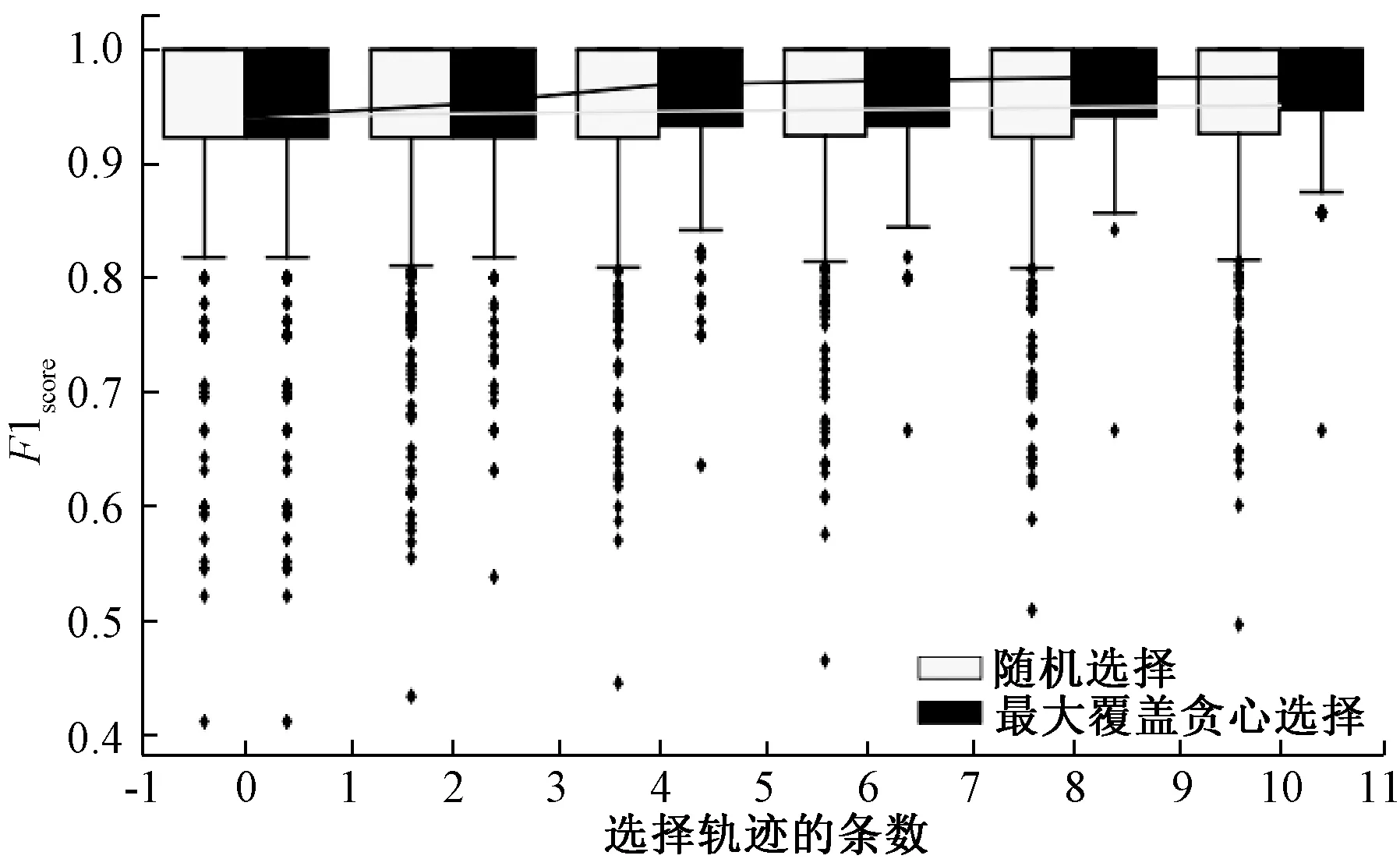
图1 孤立森林结合不同选择方式实现积水推测Figure 1 Isolation forest combined with different options to realize urban ponding water estimation

4.3.2压缩感知 本文为了验证所提算法的有效性，分析了压缩感知结合随机选择、压缩感知结合贪心选择进行实验。图2展示了两种方法的实验结果。从图2箱形图部分可以看出，贪心选择2条轨迹对应的箱形图的上四分位数、下四分位数、中位数、上限、下限都重合。随着选择轨迹条数的增多，贪心选择对应的箱型图的上限不断提升。图2折线部分是对2019年5月9日至31日内每小时分别进行积水推测得到的F1score取均值的结果，可以看出，随着选择轨迹条数的增多，贪心选择和随机选择的F1score不断提升，且贪心选择的F1score提升效果优于随机选择。贪心选择4条轨迹的F1score明显高于贪心选择2条时，但在选择条数继续增多时，F1score提升不明显，根据结果及数据分析，是由于在选择轨迹条数增多时，由于未覆盖的站点越来越少，贪心选择的轨迹覆盖的站点数也在减少，因此导致提升不明显。综上所述，基于压缩感知实现积水推测时，贪心选择对推测准确度的提升效果优于随机选择，且随着选择轨迹条数的增多，准确度也随之提升。

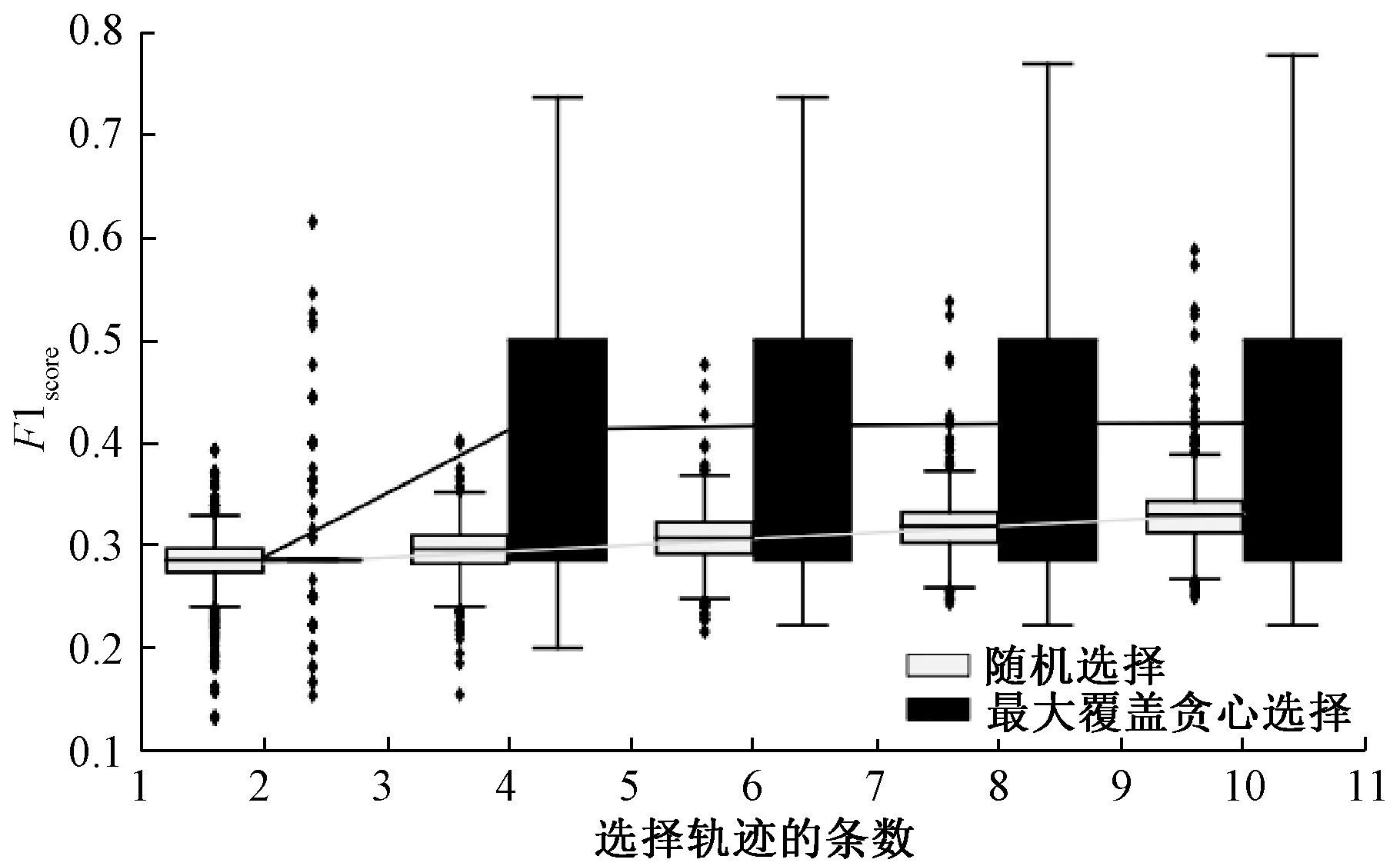
图2 压缩感知结合不同选择方式实现积水推测Figure 2 Compressed sensing combined with different options to realize urban ponding water estimation

5 总结

本文通过网格化深圳市部分区域，并将积水监测站点、滑动雨量监测站点映射至网格来融合深圳市滑动雨量数据、深圳市水务局积涝水位数据。使用孤立森林算法，对深圳市148个积水监测站点从2019年5月9日至31日每小时的积水状态进行预推测。最后，结合群智感知思想选取公交车感知轨迹生成感知数据，以此提升了推测准确度。本文采用F1score作为模型的评价指标，实验结果表明通过孤立森林算法推测城市积水是可行的，而贪心选择公交车感知轨迹生成感知数据能够提升推测准确度，且效果优于随机选择。

在将来的工作中，本文计划加入数字高程模型、不透水地面指数等特征来优化模型。同时，也计划在感知轨迹选择阶段采用主动学习方法，推测阶段考虑用深度学习[17]的方法提升选择轨迹生成的感知数据对推测准确度的作用。