基于耐震时程法的进水塔结构抗震性能分析
赵 杰, 杨 杰, 李晓娜
(西安理工大学 西北旱区生态水利国家重点实验室, 陕西 西安 710048)
0 引言
进水塔在地震作用下的正常运行和自身抗震性能对整个水利工程至关重要。针对进水塔的动力学研究已有部分成果[1-5],张汉云等[6-7]研究分析了地震持续时间和频率对进水塔抗震性能的影响,并研究了进水塔中TMD系统对地震能量的分散作用。Mohammad Alembagheri[8]对大坝进水塔-库水-地基的动力特性进行了数值模拟研究。增量动力分析(Incremental Dynamic Analysis,IDA)是一种常用的抗震分析方法[9-11],以大量时程分析为基础,但用于复杂结构时其计算速度缓慢且结果比较离散。在追求计算效率与精度的要求下,一种新型抗震评估方法——耐震时程法(Endurance Time Method,ETM)提出并得到发展[12]。耐震时程法的核心是合成一种能随时间不断增大的加速度曲线,一次耐震时程分析可以得到结构从稳定至失稳的全过程信息。近年来耐震时程法在钢框架结构[13]、支撑框架结构[14]等方面取得了较快发展。
本研究结合耐震时程的基本概念,合成3条符合我国水工抗震设计规范的耐震时程曲线,建立进水塔模型,对比研究10条天然地震动作用下结构进水塔的塔顶位移、基底剪力分布及结构的损伤历程。研究结果表明,耐震时程法可以有效预测不同动力强度作用下的结构响应,且其计算效率高、精度好,可为进水塔结构的抗震性能分析提供一种新的手段。
1 耐震时程曲线的合成
耐震时程法作为一种新兴的地震评估方法[15],其最大特点在于可以形成一条随时间加速度幅值不断增大的时程曲线,且在持续时间内加速度反应谱大小与地震持续时间t成线性关系:
(1)
式中:tTarget为目标时间;t为任意时间点;T为结构的自振周期;SaC(T)为预先制定的反应谱;SaT(T,t)为时刻t的目标加速度反应谱。
根据位移反应谱与加速反应谱的关系可知位移与加速度相关,从而得出相应时刻的位移反应谱:
(2)
式中:SuT(T,t)为时刻t的目标位移反应谱。
在任意t时刻同时满足加速度反应谱和位移反应谱比较困难,但在一定精度允许下是可以获得的,从而可以将其转化为无约束优化问题:

α[Su(T,t)-SuT(T,t)]}dtdT
(3)
式中:SaT(T,t)为时刻t的目标加速度反应谱;ag为需要生成的耐震时程曲线;α为位移反应谱的权重系数。
根据我国水工建筑抗震设计标准(GB 51247—2018)[16]中的反应谱,利用Matlab非线性最小二乘算法lsqnonlin求解式(3)的无约束优化方程[17]。取目标时间点tTarget为10 s,a=0,目标规范反应谱的特征周期Tk=0.35,合成3条持续时长20 s的耐震时程曲线。图1(a)为耐震时程曲线,图1(b)显示了耐震时程曲线在不同时间长度(0~5 s、0~10 s、0~15 s、0~20 s)下的反应谱与目标规范谱的比较,从图中可以看出二者吻合较好。
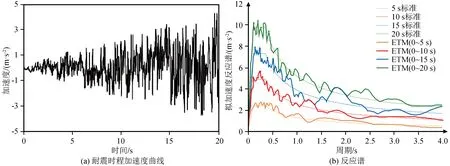
图1 耐震时程曲线及反应谱Fig.1 Endurance time curves and response spectra
2 进水塔结构有限元模型
2.1 计算模型
为研究耐震时程法在进水塔结构中的应用,以四川省汶川县沙牌水电站引水洞进水塔作为研究对象。该进水塔顺水流方向底宽为13.87 m,顶宽为25.87 m,垂直水流方向宽度为8.4 m,垂直水面方向高度为52.5 m。结构的抗震设防烈度为Ⅷ度(0.2g),场地类别为Ⅲ类。取塔前后、塔底方向1倍塔高、塔体左右0.5倍塔高范围内地基作为计算对象,建立模型如图2所示。地基底部采用固定约束,四周采用法向约束,地震动于地基底部水平顺河流向输入。
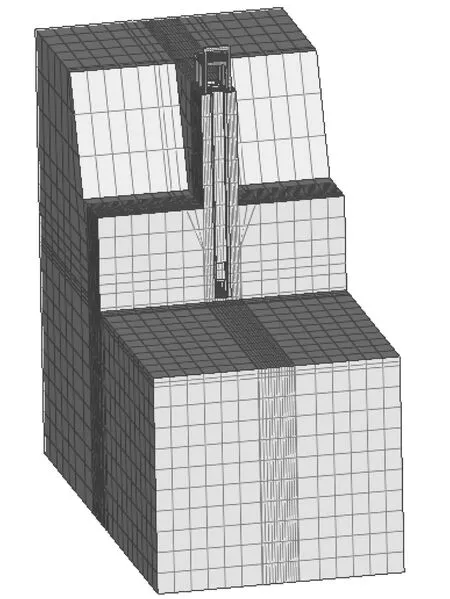
图2 进水塔结构模型Fig.2 Structure model of water intake tower
2.2 计算参数
在有限元计算中,进水塔结构主体材料为C20混凝土,材料基本参数列于表1。为简化计算,结构分析时仅考虑结构水平单向地震作用,取瑞利阻尼系数α为0,β为0.019 87。本构关系采用ABAQUS混凝土塑性损伤本构模型。取C20混凝土的膨胀角为30°,偏心率为0.1,极限强度比fb0/fc0为1.16,不变量应力比Kc为0.667,黏滞系数为0,动态抗压强度10.1 MPa,动态抗拉强度1.01 MPa。

表1 材料基本参数
2.3 地震动选取
为分析结构在不同地震水平下的抗震性能,从PEER(Pacific Earthquake Engineering Research Center)地震动数据库中选取10条天然地震动记录用于分析(表2)。采用特征周期T1对应的谱加速度Sa(T1)值等比例调幅10次,使天然地震动反应谱平均分布于0.1g~1.0g。
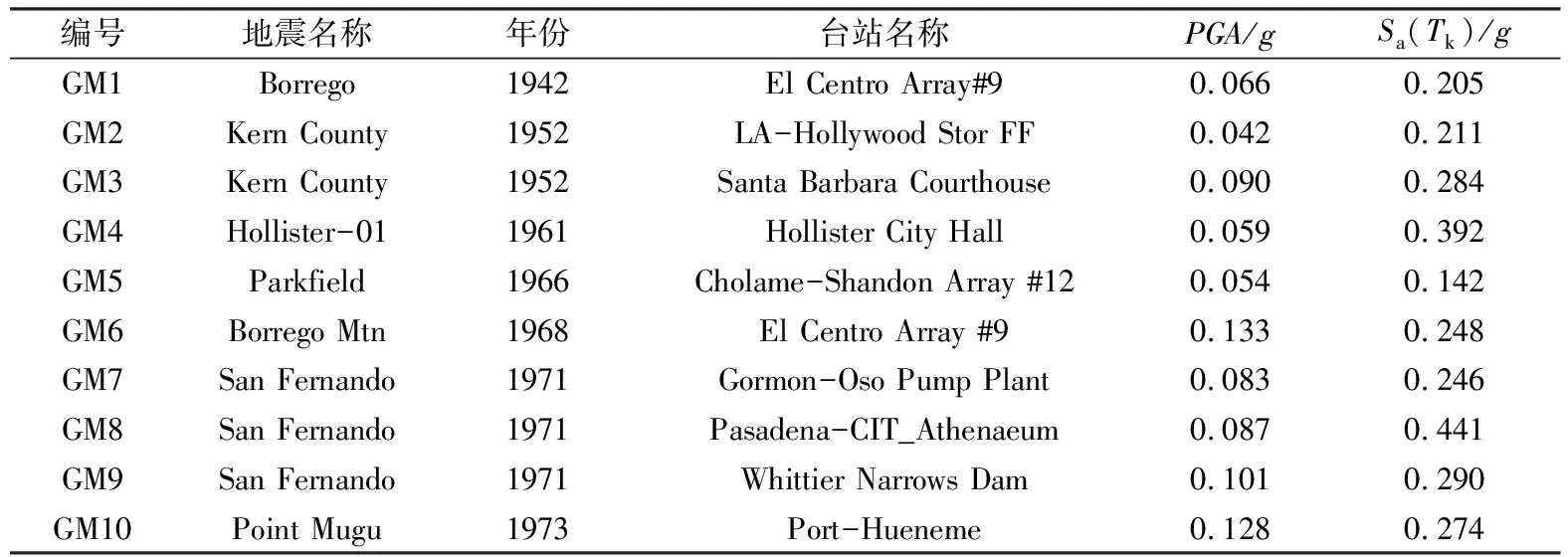
表2 10条天然地震动信息
3 基于ETM的进水塔结构抗震分析
3.1 耐震时程分析的结果表述
耐震时程法的结果可按下式确定[18]:
f(t)EDP=max(Abs(f(τ),τ∈[0,t]))
(4)
式中:f(t)EDP为时刻t的工程性能参数(Engineering Demand Parameters,EDP);f(τ)为时段[0,t]内的结构响应,对f(τ)取绝对最大值即可得到f(t)EDP。
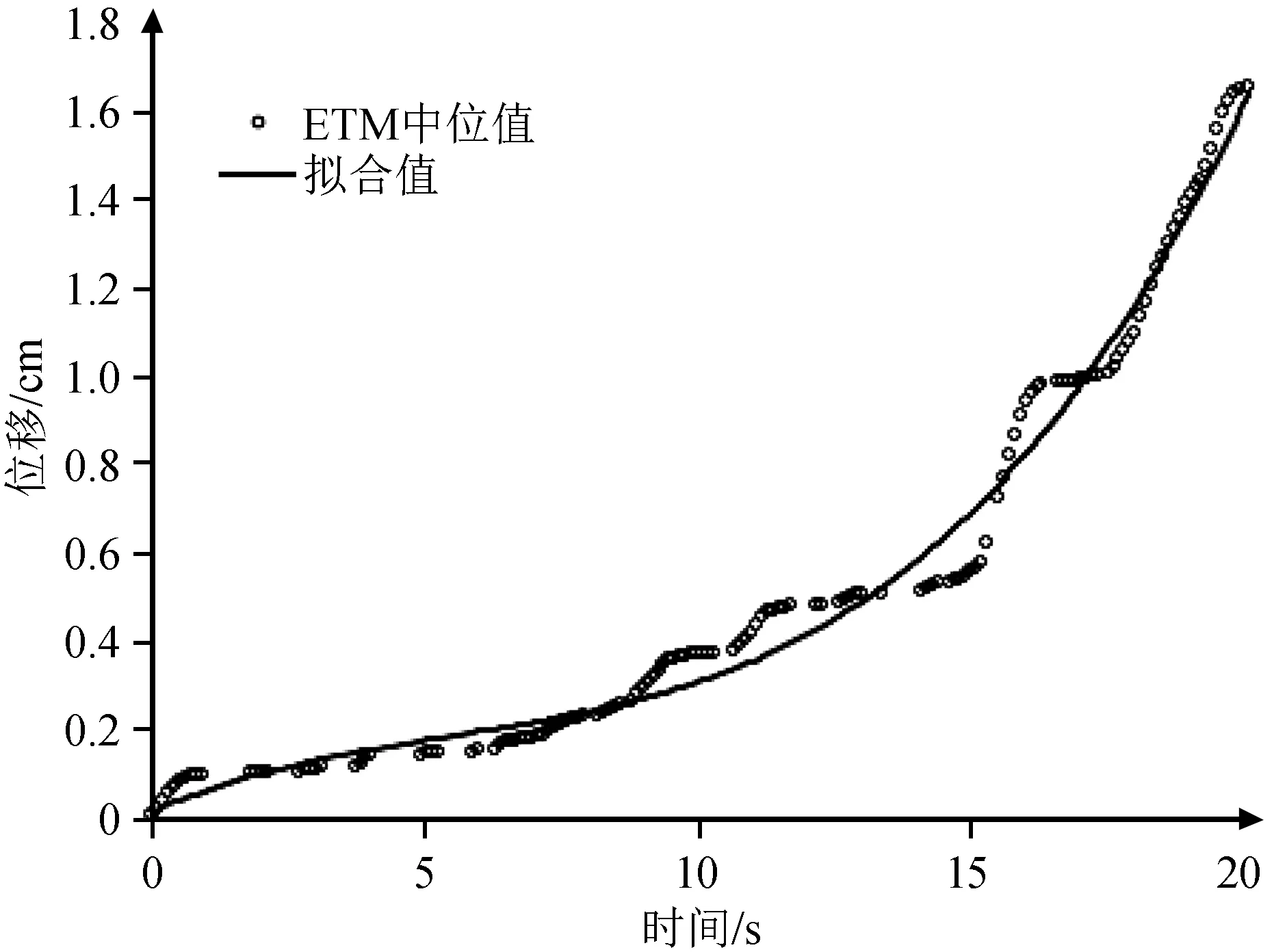
根据式(4)可以获得结构在3条耐震时程曲线分析结果下的最大塔顶位移(图3)。从图3中可知,耐震时程分析结果呈阶梯式上升,为使结果具有连续性,需将耐震时程结果的中位值进行拟合。考虑结构在微震时处于弹性状态,损伤积累较小,结构位移增长缓慢并处于一个较小值。当处于强震范围时,结构损伤累计加大,材料强度降低,结构位移响应急剧增长。因此选择三次多项式进行损伤模式下耐震时程分析结果中位值的拟合:

图3 ETM分析顶点位移及其中位值Fig.3 Vertex displacements from ETM analysis and the median value

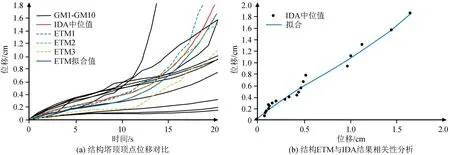
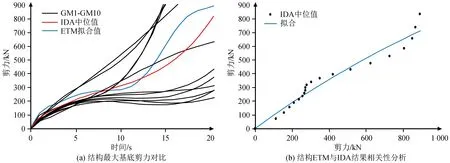
(0 (5) (6) 图4所示的光滑曲线为耐震时程结果中位值的拟合结果,拟合相关系数R2=0.984 2。从图中可以看出,拟合后的塔顶位移曲线连续、光滑,并随时间的推移其响应值不断变大,从而摆脱了由于阶梯状使得响应值在部分时间段内固定不变的缺点。 图4 ETM结果拟合Fig.4 Fitting of ETM results 耐震时程分析结果所代表的是结构在不同动力强度(耐震时间)下的抗震响应,而天然地震动的分析结果仅针对某个特定动力强度下的结构抗震响应。为进行对比分析,需要将不同动力强度的天然地震动进行耐震时间转化。等效耐震时间可按下式计算: (7) 式中:tET为单条天然地震动在不同动力强度下的等效耐震时间;γ为单条天然地震动的调幅系数;Sas(T1)为T1时对应的单条天然地震动反应谱值;Sac(T1)为T1时对应的规范反应谱值。 塔顶位移是结构抗震分析中的重要参数,是反映结构性能曲线的主要物理量。图5给出了10条天然地震动下结构的IDA结果和耐震时程分析结果。从图5(a)可以看出,在整个耐震时程持时范围内,耐震时程结果与天然地震动下的IDA结果中位值较为接近,且3条耐震时程结果均在IDA分析结果的包络线内,与IDA分析结果基本符合。为合理比较耐震时程结果与IDA分析结果,对两种分析结果进行相关性分析。在全长20 s的耐震时间内每间隔1 s取一点,得到共20点耐震时程结果与IDA结果,如图5(b)所示。针对进水塔结构,ETM结果与IDA分析结果较为接近,其相关系数为0.983 3,这表明耐震时程分析可以很好地预测结构在不同强度下的位移响应,且耐震时程分析只需要较少的结构非线性分析(3次结构分析),在一定程度上降低了计算成本。 图5 结构塔顶顶点位移对比及相关性分析Fig.5 Comparison between vertex displacements of the structure and correlation analysis 基底剪力反映了结构的抗震侧向力,是结构抗震评价的重要参数。图6给出了两种计算方法对结构最大基底剪力的分析结果。从图6(a)中可以看出,耐震时程分析结果在部分耐震时间段内会低估结构的最大基底剪力,这是由于IDA分析所采用的个别地震动强度持时较长,从而导致结构基底剪力偏大,但耐震时程结果趋势与IDA分析结果一致。从图6(b)也可以看出,IDA分析结果与耐震时程分析结果呈二次相关,其拟合相关系数R2=0.95。总体来说,耐震时程法能以较小的误差预测结构的基底剪力。 图6 结构最大基底剪力对比及相关性分析Fig.6 Comparison between the maximum base shear of the structure and correlation analysis 通过ABAQUS软件非线性时程分析得到结构在不同动力强度下的响应(图7)。由于损伤区域集中于进水塔底部区域,为更好地观察损伤的发展状态,图7给出了两种分析方法在部分时刻的局部等值线损伤分布图。图7(a)、(b)、(c)分别显示了进水塔结构初次损伤、进一步损伤及整个耐震时程作用结束时的损伤,图7(d)、(e)、(f)分别显示了调幅后的地震动GM7致使结构出现首次损伤、损伤发展及对应耐震时刻20 s时的损伤分布。从图7(a)~(c)可以看出:在6.3 s前,耐震时程结果显示结构基本处于未损伤状态;6.3 s后,结构损伤集中于进水塔前端底部区域,受到耐震时程逐渐加大的水平向动力作用,损伤逐步向进水塔后端发展,直至整个耐震时程作用结束,结构底部大部分区域损伤值已达0.9,塔身进水段墙壁已全部出现损伤。对比图7(d)~(f)可知,天然地震动下的初始损伤仅代表结构在不断调幅后初次出现的损伤,而非结构在地震作用下的初次损伤,且无法表达结构出现初次损伤的具体调幅值,在这一点上耐震时程法极大节约了计算时间,并能有效表达结构的初次损伤分布情况。对比图7(b)与(e)可知,由于受到不同天然地震的作用,结构损伤发展的分布存在一定差异性。对比图7(c)与(f)可知,结构最终损伤的分布情况接近一致,这是由于二者均已达到结构所能承受地震作用的极限。对比二者的计算成本,增量动力分析法需要经过多次调幅才能表达结构在间断动力强度作用下的损伤历程,且计算耗时较长,而耐震时程法仅用3次分析即可表达结构在不同动力强度作用下的连续损伤发展状况,一定程度上解决了由于调幅导致的间断动力强度作用间的损伤状况不明问题。 图7 结构损伤等值线分布对比分析Fig.7 Comparative analysis of isoline distribution of structural damage 本研究合成了3条耐震时程加速度曲线,采用ABAQUS软件建立进水塔模型,选取10条天然地震波进行IDA分析,并与耐震时程分析结果进行对比,得到如下结论: (1) 耐震时程分析结果与天然地震动结果存在一定差异,但结果中位值误差较小,具备较好的相关性。 (2) 耐震时程法可以很好地预测到结构在不同动力强度下的整体响应,如最大塔顶位移、基底剪力等,还能较好地分析材料经过逐步增强的动力作用后在某一特定强度下的损伤分布。 (3) 耐震时程法可以利用较少的非线性分析次数得到结构整体的抗震响应,提高结构分析的效率,对于复杂结构具有较大优势。 综上所述,耐震时程法作为一种新型的结构抗震分析方法,在结构响应预测和结构抗震性能评价方面具有较大优势,为水利工程进水塔抗震设计提供了一种新方法。由于耐震时程法是一种新兴的结构抗震分析方法,如何在进水塔混合结构的抗震设计中进行应用,仍需进一步探讨与研究。

3.2 进水塔塔顶位移分析对比
3.3 结构最大基底剪力分析对比
3.4 结构损伤分布

4 结论

