汶川地震频次场异常特征分析

马禾青, 杨明芝, 罗国富

(1. 宁夏回族自治区地震局, 宁夏 银川 750001; 2. 宁夏土木工程防震减灾技术中心, 宁夏 银川 750021)

0 引言

在各种变量中,表征地震活动的物理状态和物理性质最重要的两个变量是地震频次和地震能量。针对地震能量场问题已经开展过许多工作:杨明芝等[1-2]引用随机场概念,通过自然正交展开方法研究了宁夏及邻近地区地震活动能量场问题;并在此基础上,通过大量震例研究了大地震前区域能量场的时间因子异常特征,取得了有意义的结果。马禾青等[3-4]分析了2010年4月14日青海玉树7.1级地震前震中周围和沿玉树断裂带区域地震能量场的时间变化特征,以及在一定条件下地震活动能量场和频次场的统计特征及地震活动场的平稳性问题。罗国富等[5-7]分别讨论了甘东南至陕甘宁交界中强震危险区、2013年岷县—漳县6.6级地震前震中区域以及2014年景谷6.6级地震震中区域地震活动能量场的时空特征。其他方面的工作有杨明芝等[8]以地震应变场作为地震活动的变量,通过自然正交函数展开方法计算了中国大陆6级以上强震前的地震应变场,提取出震前时间因子的异常变化。MA等[9]则针对地震活动场的几个普遍问题展开了讨论。

针对2008年5月12日汶川8.0级地震能量场开展的工作有:杨明芝等[10]采用自然正交函数展开方法讨论了汶川8.0级地震前沿龙门山断裂带地震活动能量场的时间变化,发现地震前沿龙门山断裂带能量场几个主要特征值对应典型场的时间因子出现非常明显的短期上升变化,可能是该次地震的短期异常信息。罗国富等[11]研究了汶川8.0级地震前地震活动能量场中短期异常。随后杨明芝等[12]研究了汶川8.0级地震前沿龙门山断裂带能量场的变化。

本文将在上述研究的基础上,详细讨论2008年汶川8.0级地震前地震活动频次场问题。

1 地震频次

某个区域单位时间内发生的大于一定震级地震的次数N(或地震发生率v)称为地震活动频次。地震活动频次是衡量一个地区地震活动状态的重要标志,通常具有如下特点:

(1) 地震的发生因地区而异。从震中分布图可以看出有些地区地震分布密集,有些地区分布稀疏。显然,同样的时间段内分布密集的地区地震发生频繁,分布稀疏的地区地震发生较少。图1(a)是1980—2000年汶川8.0级地震震中周围地区的地震次数分布。从图中能够看出地震发生次数等值线分布的大体轮廓,龙门山断裂带西北以及东南一带等值线密集分布,而在区域东部的四川盆地则几乎没有地震分布。地震密集的区域频次高,相反,地震分布少的区域频次低。地震频次分布与空间位置关系密切,特别是与区域的地震构造密切相关。

(2) 地震发生频次随时间变化。一个地区发生的地震有时候频繁,有时候相对平静。图1(b)绘制了汶川8.0级地震震中周围地区时间单位取3个月的地震频次-时间曲线。地震频次在平均值28.0附近波动变化。

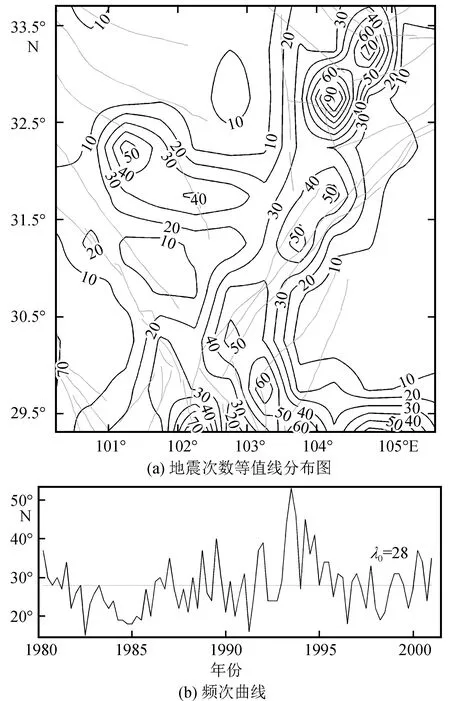
图1 汶川8.0级地震震中周围地区1980—2000年 地震次数分布和频次曲线(ML≥ 2.5)Fig.1 Earthquake frequency distribution and frequency curve in epicenter area of the Wenchuan MS8.0 earthquake from 1980 to 2000 (ML≥ 2.5)

地震频次是地震活动的本质要素之一,在一定程度上反映了区域的平均应力水平和地震构造强度的性质。事实上,如果一个地区处于应力场的作用下,可以定义由加载在区域边界上的外力所控制的平均应力σ0和平均强度S0,该地区地震发生的频次即决定于这个区域的σ0和S0。但区域内部不同部位所承受的局部应力σ和强度S并不相同,而是以随机的方式变化,因此决定了区域内不同部位地震的发生频次存在差异性和随机性。区域内不同尺度的断块交界处是应力易于集中的部位,特别是断裂构造附近,但同时也是强度相对薄弱的部位,因此是地震易发生的部位。而在应力水平相对较低的部位,或破裂强度较高的部位,地震的发生频次相对较低。

从时间上说,区域内应力随时间发生变化。由于加载在区域边界上的外加应力发生变化,或由于块体之间的相互牵引等因素,再加上地震孕育过程的影响,造成地震频次随时间发生变化。因此,一个地区的地震活动频次及其变化反映了区域的一种物理状态特征。

一次破坏性大地震绝对不是突然之间爆发的,它需要在相当大的空间范围内逐渐积累起弹性能量,再经历较长时间的孕育过程,从缓慢的量变直至突变。在未来可能发生强烈地震的区域及其周边较大范围,地震活动频次将出现反常变化,这就是研究地震活动频次场的出发点。

2 地震频次场

地震频次是随机变量,是空间以及时间的函数,称为地震活动频次场f或地震频次场。

为了描述地震频次场,采用能量场的方法[1],先将区域网格化,按网格统计地震频次场f的值,并表示为矩阵形式:

(1)

式中:fij(i=1,2,…,m,j=1,2,…,n)是第i个时段、第j网格的地震频次观测值。

将式(1)表示的频次场f进行自然正交函数展开,求解相关矩阵(协方差矩阵)R=f′f的特征值和特征向量。根据特征向量的权重系数矩阵求得时间因子序列,进而分析典型场时间因子的时间变化特征,寻找与大地震的关系[2]。地震频次场是描述地震发生频次时空特征的一种数学方法。

以下研究2008年汶川8.0级地震频次场自然正交函数展开的异常变化特征。

3 汶川8.0级地震频次场分析

选择汶川8.0级地震震中附近区域(30.0°～33.0°N、101.5°～105.5°E)为研究区,区域内1998年1月—2008年3月平均每3个月发生的地震次数为λ0=12.2。图2是该时段研究区地震频次曲线,反映了区域地震频次随时间的变化情况。可以看到,地震频次在均值线附近波动,2000年出现过1次高值,2004年底至2006年的频次较高,汶川8.0级地震前似有升高现象。

图2 1998年1月—2008年3月地震频次曲线 (2.5≤ML≤5.5) Fig.2 Earthquake frequency curve from January 1998 to March 2008 (2.5≤ML≤5.5)

3.1 自然正交函数展开结果

应用自然正交函数展开方法对研究区地震观测资料进行处理。考虑到地震频次场展开时级数收敛较慢,根据实际经验,区域按照1.0°×1.0°进行网格化,共划分为n=12个网格。地震震级范围取2.5≤ML≤5.5,并删除余震。资料时段取1998年1月—2008年3月,采样时间间隔取3个月,时间点数m=41。

需要特别说明的是,在研究地震频次场时,选择合适的震级上下限十分重要。震级下限一般由研究区域的地震监测能力决定;而震级上限则考虑区域内处于正常地震活动水平时所发生的上限地震震级,因此这里震级范围取2.5≤ML≤5.5。采样时间间隔取3个月是因为考虑了区域地震活动的平均状态,即该区域1998年以来平均每3个月发生的地震次数为12.2,这样选择能够保证应用自然正交函数展开方法对该区域地震观测资料进行处理时拥有足够的样本量。

计算出区域12个网格41个时间段观测到的地震次数、平均值和距平值,以矩阵(1)的形式按顺序给出频次场f,得到一个41×12阶矩阵。求解协方差矩阵R=f′f,得到12个特征值λk(k=1,2,…,12)和相应的特征向量(典型场)Xk(k=1,2,…,12),然后计算求得典型场的时间因子Tk。

表1列出了地震频次场自然正交函数展开的前4个特征值和相应典型场的贡献率。由于典型场是按照对应的特征值由大到小的顺序排列,较大的特征值所对应的典型场在频次场中所占比重就较大,可以看到相应的典型场对总场的贡献率依次减小。

表1 汶川8.0级地震频次场特征值及贡献率

3.2 频次场的典型场

汶川8.0级地震周围区域频次场自然正交函数展开为由12个典型场所叠加的级数和形式。每一个典型场又分别是由12个分量组成的向量,均代表地震频次的一种空间分布类型。表2列出前4个特征值所对应典型场的分量值,图3是这4个典型场的等值线图。可以看到,频次场典型场与能量场的典型场[1-3]有很大区别,前者的分量中找不到一个占绝对优势的分量值,等值线分布也不如能量场那样集中,很难说哪个典型场能够占到绝对优势,但也并未显示出平均分布。如第1分量为第3典型场占优势,第2分量为第4典型场占优势,第3分量为第1典型场占优势,第8分量为第2典型场占优势。

表2 汶川8.0级地震频次场前4个典型场的分量值

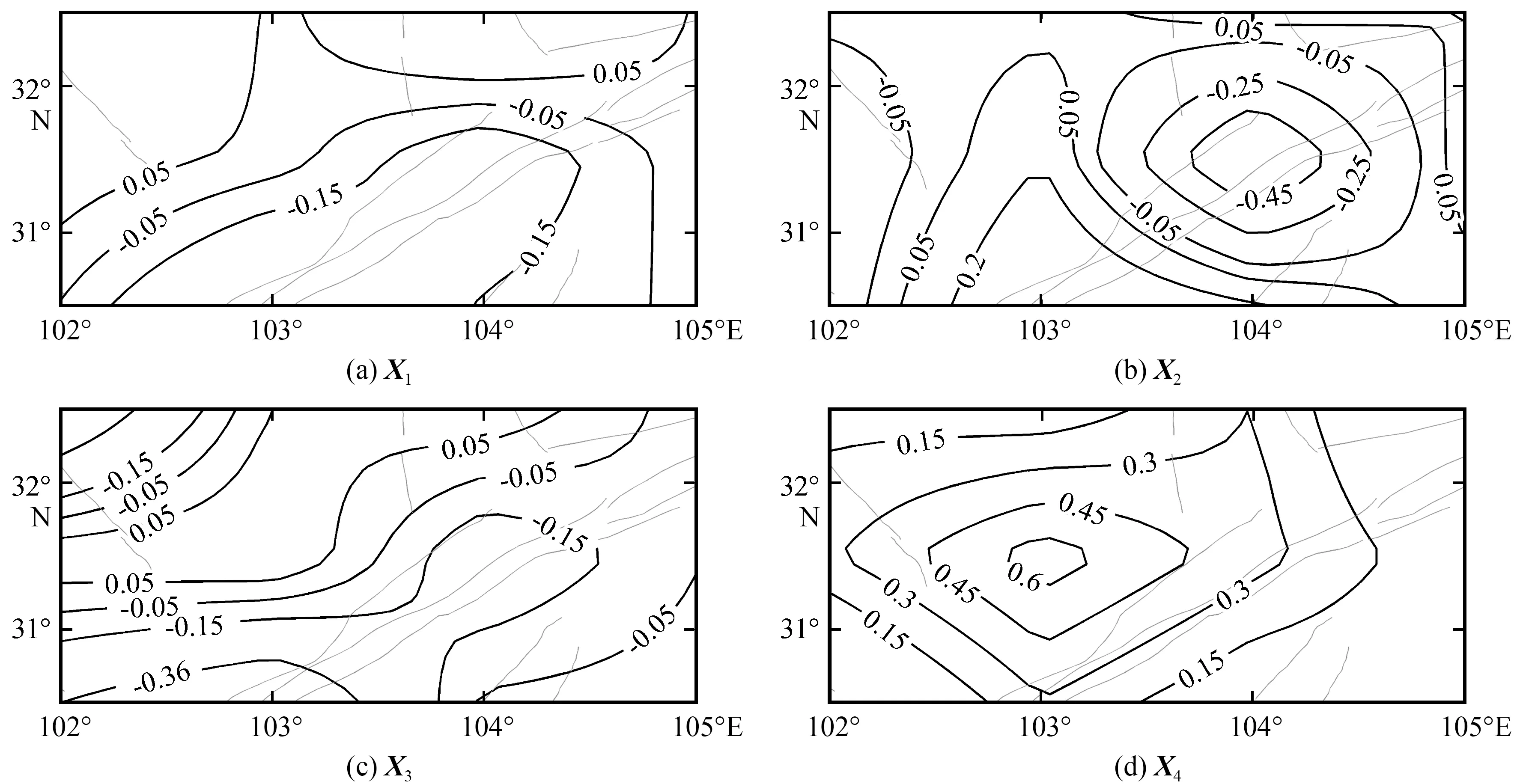
图3 汶川8.0级地震频次场前4个典型场的等值线分布Fig.3 Isoline distribution of the first four typical fields of Wenchuan MS8.0 earthquake

3.3 频次场时间因子异常分析

通过自然正交函数的展开计算,求得典型场的时间因子Tk(k=1,2,…,12)。表3列出了前4个特征值对应典型场的时间因子序列。图4是震前区域地震频次场前4个典型场的时间因子曲线。图中红线表示均方差,均方差高值和低值即为判定是否出现异常的标准,如震前3年曲线超过红线可以认为出现了异常。从图4中可以看出,汶川8.0级地震频次场前3个典型场的时间因子大约从2005年前后开始出现异常。第1典型场从2004年9月起波动变化,相继出现3个超出均方差的高值点和2个低值点;第2典型场于2005年6月出现1个低值点后波动上升,震前达到最高值3.227 8;第3典型场在2004年12月掉至最低点-3.480 3,然后逐渐恢复到正常水平。此外,在汶川8.0级地震发生前的1个多月,第2典型场出现大大超过均方差的高值,表现出短临异常的特征。前4个典型场中只有第4典型场无异常显示。前4个典型场占总场比重为0.661 2,其中异常典型场所占比重为0.548 3。

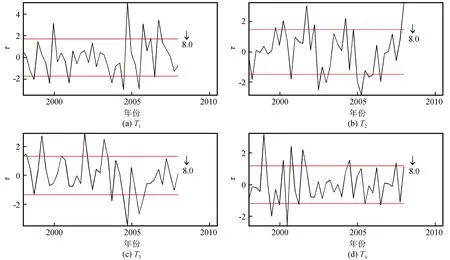
图4 2008年汶川8.0级地震频次场前4个典型场时间因子曲线Fig.4 Time factor curves of the first four typical fields of frequency fields of Wenchuan MS8.0 earthquake, 2008

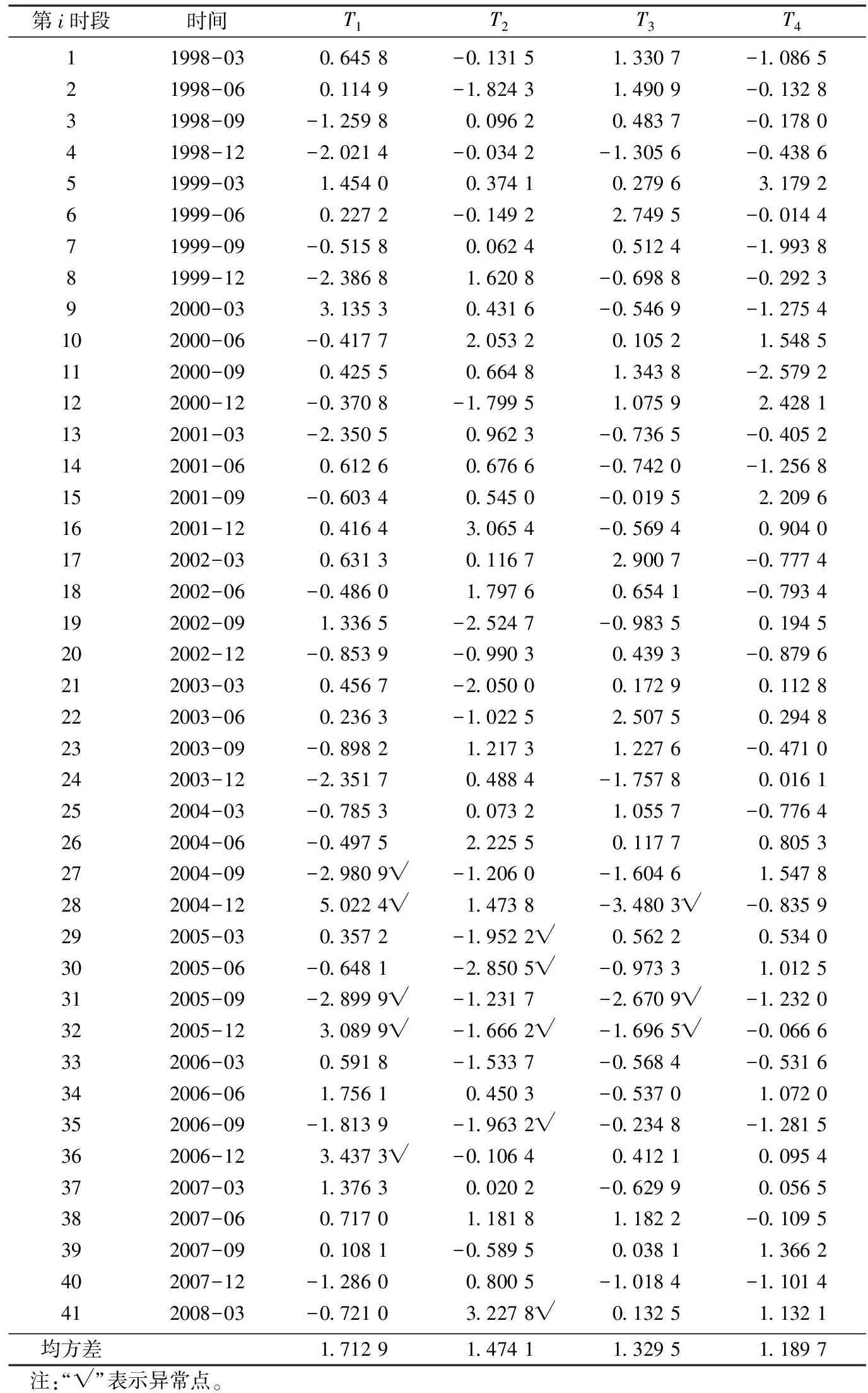
表3 汶川8.0级地震频次场前4个典型场的时间因子

为了进一步分析频次场反映的异常,图5给出了汶川8.0级地震频次场第5至第8典型场的时间因子曲线,其中第5、第7和第8典型场出现了超出均方差的异常变化,且第5和第8典型场显示的异常具有短临异常的特点。

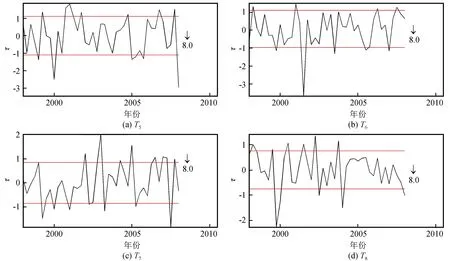
图5 2008年汶川8.0级地震频次场第5至第8典型场时间因子曲线Fig.5 Time factor curves of the 5th-8th typical fields of frequency fields of Wenchuan MS8.0 earthquake, 2008

由于地震频次场受较小震级地震的影响较大,各个网格的频次不如能量场那样差别较大,展开的收敛速度较慢,大地震前的异常也不同于能量场那样集中在前3～4个典型场,而是体现在更多的典型场中。汶川8.0级地震频次场前4个典型场的拟合精度只有0.661 2,当取前8个典型场时,拟合精度达到0.936 8。这8个典型场中有6个典型场显示出异常变化,异常典型场占总场的比重为0.691 1。

汶川8.0级地震能量场前4个典型场的拟合精度为0.994 5[3],而频次场前8个典型场的拟合精度为0.936 8,可见频次场较能量场的级数收敛要慢得多。

4 计算参数改变的影响

4.1 起始震级较大时的频次场及分析

可以看到,图4～5中的曲线起伏波动较大。我们知道,区域地震活动包含正常的背景活动和大地震孕育作用下的异常活动,中小地震在频次场中发挥了较为重要的作用。但是较小的2～3级地震应当主要反映区域的背景活动,起始震级偏低的话可能会导致背景活动掩盖异常活动,使得异常显示不够清晰。较大的地震则更多受到孕震机制的控制,能够更好地反映地震孕育过程中的异常活动。因此将计算频次场时的震级下限提高至ML4.0,得到汶川8.0级地震频次场前4个典型场的时间因子曲线(图6)。从图6中可以看到,频次场时间因子的异常形态更加完美、清晰,短期的上升或下降异常的变化幅度更为突出。前4个典型场的拟合精度为0.851 2,较震级下限为ML2.5时有了显著提升,表明汶川8.0级地震前的异常活动主要体现在ML4.0以上的地震活动上。但是由于ML4.0以上地震发生得较少,自然正交展开结果绝大部分时间都在均值附近波动变化,因此建议在较低震级下限的计算基础上加以分析。

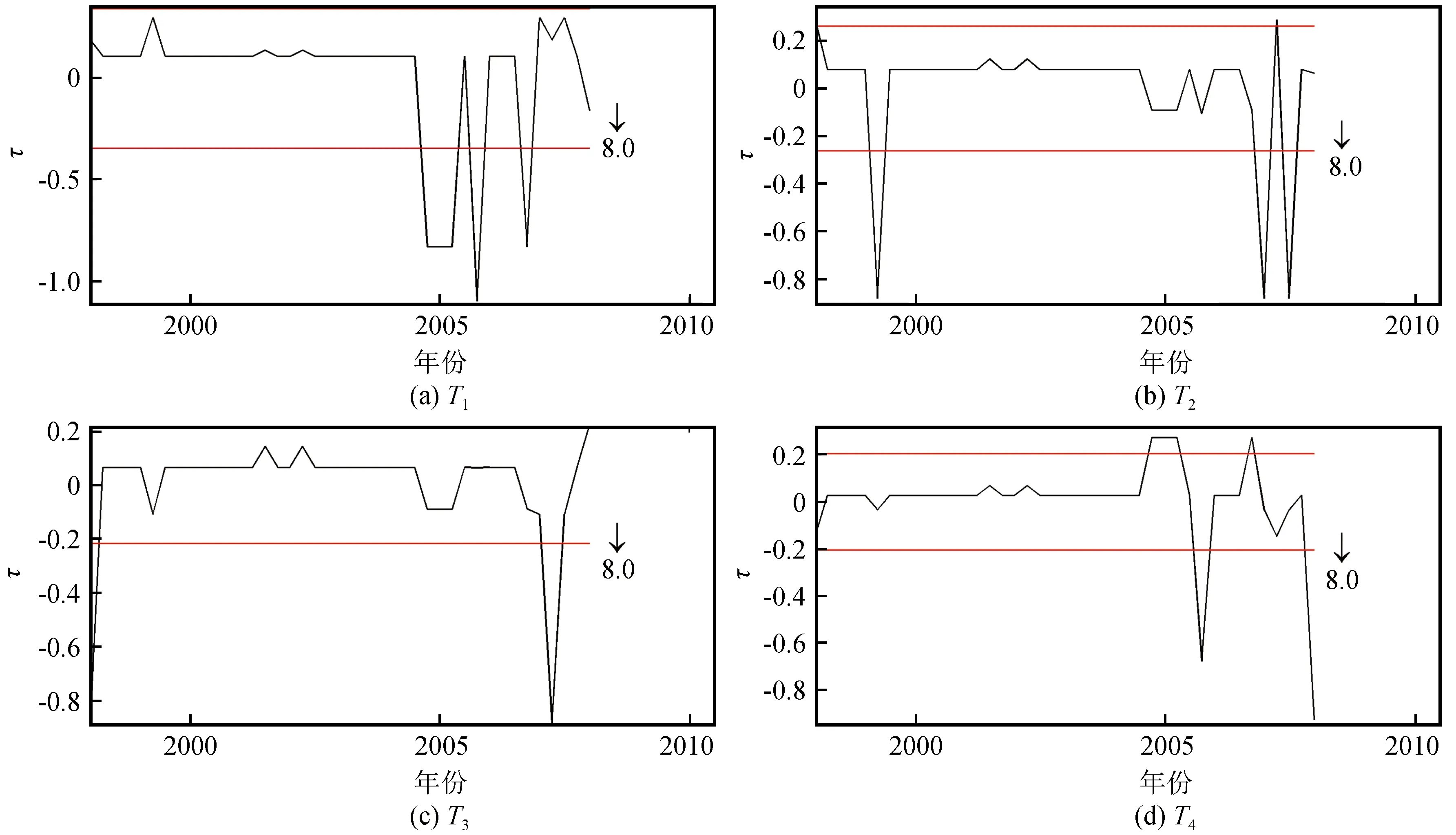
图6 起始震级较大时汶川8.0级地震频次场前4个典型场时间因子曲线Fig.6 Time factor curves of the first four typical fields of Wenchuan MS8.0 earthquake with larger initial magnitude

4.2 网格划分问题

在计算汶川8.0级地震的能量场问题时[1-3],区域是按照0.5°×0.5°的尺度进行网格化的。如果按照同样的网格化尺度来计算汶川8.0级地震的频次场,展开的级数会收敛得非常慢。前8个典型场的拟合精度仅为0.574 2,取到前21个典型场时才能达到0.903 3的拟合精度,而汶川8.0级地震能量场前4个典型场的拟合精度就已高达0.999 6。可见按0.5°×0.5°的尺度进行网格化,地震频次场展开的收敛速度相较能量场要慢得多。事实上,由于地震频次主要受到小地震的控制,而地震能量主要受到大地震的影响,地震频次与能量在时空分布上往往并不十分一致。统计网格过小会使得频次的空间差异变小,不利于突出场的变率差别。

5 讨论

张致伟等[13]在研究汶川8.0级地震前龙门山断裂带的地震活动性特征时,得到有小震监测资料以来,龙门山断裂带地震活动持续平稳发生,汶川地震前该地区地震活动增强或平静异常现象不明显。李永莉等[14]在分析汶川8.0级地震前的地震活动频次时,得到2002—2008年龙门山断裂带及附近地区出现了6年的区域性中小地震活动增强现象。陈学忠等[15]利用统计参数,发现汶川8.0级地震前龙门山断裂带ML≥ 3.0地震活动半年频度分布表现出明显的异常变化,在汶川地震前ML≥ 2.0地震活动月频度分布出现异常变化。可见,识别汶川地震前地震活动的增强或平静异常较为困难。从李永莉等[14]在分析频次中得到的震前6年的区域性中小地震活动增强到陈学忠等[15]利用统计参数得到的ML≥3.0地震活动半年频度分布以及ML≥2.0地震活动月频度分布异常变化无疑已经前进了一大步,利用地震活动频次场方法得到的结果似乎更为乐观。

本文的研究表明,通过自然正交展开方法研究汶川8.0级地震的地震活动频次场问题是可行的。当取前8个特征值对应的典型场时,有6个典型场显示出异常变化,异常典型场占总场的比重为0.691 1;异常最早出现在2004年9月,即震前3年7个月,之后陆续出现,最迟的在震前1个多月出现,表现出从中期趋势背景异常到短期趋势异常,再到临震异常的特征。由于研究区涵盖了汶川8.0级地震的发震构造,不妨认为其覆盖了汶川8.0级地震的孕震区。汶川8.0级地震前以自然正交方法分析得出的地震频次场的种种异常变化皆是孕震过程中出现的异常,因此利用自然正交方法能够更为清晰地提取汶川8.0级地震前地震活动频次出现的异常。