再入航天器周围等离子体分布特征研究

吴祥东， 车学科， 狄 辉， 韦洋红

（航天工程大学 宇航科学与技术系， 北京 101416）

0 引言

在距地面20～100km 的空域， 航天器再入过程中表面会产生等离子体鞘套。 等离子体鞘套使入射电磁波能量发生衰减，当这种衰减达到一定程度时，电磁波将无法通过等离子体鞘套，这种现象称之为黑障[1-7]。减弱黑障对航天器的飞行安全具有重要现实意义。

掌握航天器周围等离子体分布特征是研究电磁波在等离子体鞘套中传输的基础。 对其进行计算仿真会牵涉到很多方面。

在控制方程方面，主要包括粘性流动的纳维-斯托克斯（Navier-Stokes，N-S）方程，以及无粘流动的欧拉（Euler）方程。 目前常用的控制方程多为N-S 方程。

最常用的化学反应模型包括：Gupta 化学反应模型[8]（11 组分），Park 化学反应模型[9]（7 组分）和Dunn-Kang 化学反应模型[10]。

激波计算方法主要包括激波装配法和激波捕捉法。实际应用中较多的使用激波捕捉法。

Kim[11]等使用计算流体力学方法计算航天器周围的流场分布及等离子体密度分布。 美国针对洲际导弹通信需求，开发了等离子体流场模拟程序[12]。Takahashi[13-14]等人使用计算流体力学工具计算等离子体分布， 然后使用具有修正介电常数的时域有限差分解算器计算等离子体的存在。Starkey[15]使用一维有限体积无粘解算器估算了高超声速航天器沿其轨迹的等离子体密度。

黄华[16]等采用11 组分化学反应模型和双温模型计算FIRE II 飞船的热化学非平衡流场参数分布。 董维中[17]等利用计算流体力学代码求解N-S 方程， 对半球模型和球锥模型的流场分布进行数值计算， 并将结果与参考文献进行对比，结果良好。

本文的主要内容如下： ①对再入航天器周围等离子体分布进行建模和仿真，得到等离子体电子数密度分布；②与文献中的仿真结果和飞行试验结果进行比较， 验证模型的有效性； ③分析不同飞行高度下等离子体参数的变化； ④分析不同参数对航天器头部等离子体厚度及峰值电子数密度的影响。

1 计算模型与仿真校验

1.1 高超声速流体模型

守恒形式N-S 方程用于模拟多种反应可压缩流。 公式（1）～（3）分别为流体质量、动量和总能量的守恒方程。方程（3）中的总能量是流体的内能、动能和化学能的总和。 公式（4）和公式（7）中求和的上限是系统中组分的总数。流体假设为牛顿流体，并遵循体积粘度为零的斯托克斯假设。 此外，对于状态方程，流体遵循理想气体定律：

式（7）右边项分别为内能、动能和化学能；γ—气体比热比；H—生成焓；cp—恒压下的比热。

1.2 等离子体组分模型

式（9）表示对于每种组分，分别满足整体流体中单个组分的质量守恒。速度u→与整体流体的速度相同。式（9）的右边项表示由于化学反应引起的组分密度的变化率。 在给定的化学反应中， 组分密度变化率由正向和反向反应速率以及反应物和产物的现有密度数获得。 所有反应中组分i 的变化率相加得到si：

1.3 组分属性

利用式（14）～式（16）可以从气体动力学理论中获得单个组分的粘度、热导率和比热。 式（13）～式（16）中的流体热导率k 和粘度μ 由摩尔分数平均法获得， 定压比热cp由质量分数平均法获得， 气体常数R 由摩尔分数换算分子量计算得到：

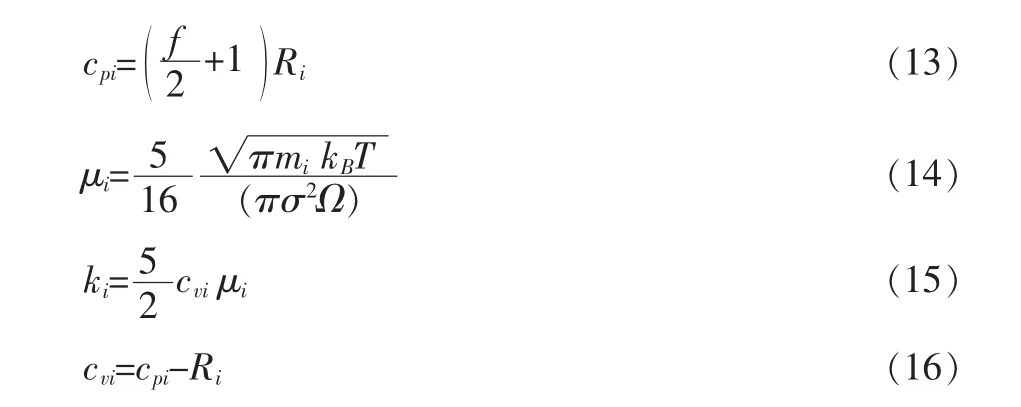
其中f—自由度数；kB—玻尔兹曼常数；σ—碰撞直径；Ω—碰撞积分；cv—定容比热。

1.4 仿真校验

对RAM CII 航天器高速再入大气层的过程进行仿真， 计算域如图1 所示：L1=0.205m，L2=1.295m，L3=0.8524m，L4=1.1m，R=0.1524m，δ=9°。RAM CII 航天器的外形数据取自文献[18]，忽略安装在表面上的探头。 航天器的高度在61km 左右，速度7650m/s，约23.9 马赫。 用于模拟的网格如图2 所示。

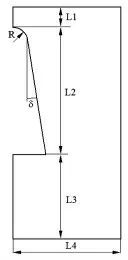
图1 仿真区域Fig.1 Simulation area

考虑七组分化学反应模型，组分分别为N2、O2、N、O、NO、NO+和e-，不考虑烧蚀。 反应速率参照文献[19]。 来流从图2 的顶部流入。

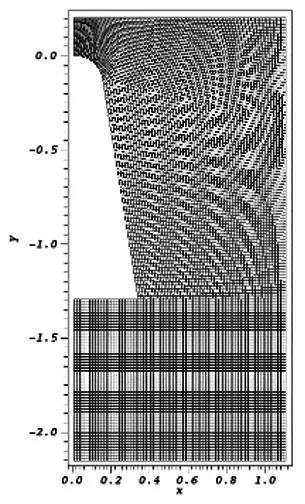
图2 网格划分Fig.2 Meshing

连续方程用标准的MUSCL 格式求解，采用激波捕捉法处理间断，采用Runge-Kutta 格式进行时间积分。

图3 为流场中的电子数密度分布仿真结果， 图4 为文献[20]中电子数密度分布。全流场的分布结果对比较为一致，最高电子数密度分别为1.14×1020m-3、1.2×1020m-3，误差为5%，都存在于航天器头部区域。

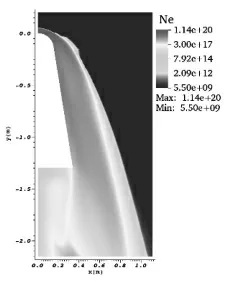
图3 电子数密度分布Fig.3 Electron number density distribution

图4 文献[20]中电子数密度分布Fig.4 Electron number density distribution in [20]

图5 显示了航天器表面不同位置处等离子体峰值电子数密度仿真结果与文献[18]中微波反射计测量值的比较。测量值是由15 个不同频率的微波反射计测量的电子数密度得到的时间平均值，这些反射计位于航天器表面三个位置，沿着y 轴距航天器头部顶端的距离分别为0.23m、0.7m、1.04m。 图中实心正方形表示试验测得的结果，实心圆表示仿真结果，实线表示两组数据点的曲线拟合。

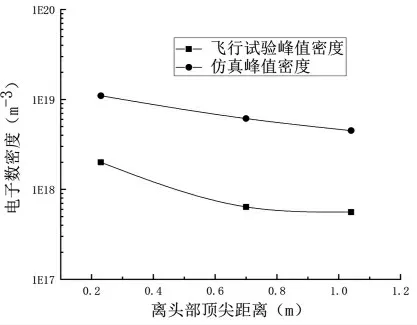
图5 峰值电子数密度比较Fig.5 Comparison of peak electron number density

飞行试验测量结果比仿真结果小约一个数量级，这可能与飞行试验流场中由于烧蚀产生的碱性物质降低了电子数密度有关， 而仿真考虑的是洁净空气。 从趋势来看，比较显示了良好的一致性；从设计的角度来看，就安全系数而言，这种程度上模拟的值是可以接受的。由此可以认为此种模型及数值方法用于计算再入航天器周围等离子体分布是可行的。

2 参数对等离子体分布影响分析

用于仿真的飞船模型为钟型结构，最大直径2.5m，高2.5m，计算区域为对称轴的一边，网格划分如图6 所示。

图6 飞船网格划分Fig.6 Spacecraft grid division

2.1 飞行高度

分别选取飞行高度71.6km、61km、45.7km、29km、21.3km对飞船周围等离子体分布进行仿真，得到峰值压强、峰值温度和峰值电子数密度随飞行高度的变化，如图7 所示。

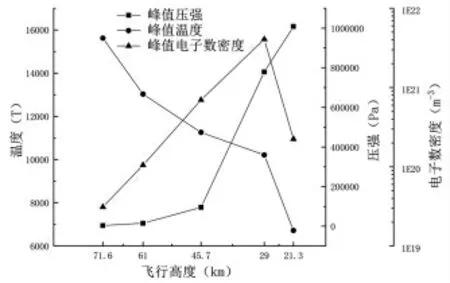
图7 峰值压强、温度、电子数密度随高度变化Fig.7 Peak pressure，temperature，electron number density vary with height

由图可知，在71.6～21.3km 的高度范围内，峰值压强随高度的减小而增大，这时航天器的速度虽然有所改变，但是空气本身的压强随着高度的减小而增大， 这是峰值压强随高度变化的主导因素。

峰值温度随高度的减小而减小， 这主要是因为航天器飞行高度减小时，航天器的飞行速度减小，导致激波后的流体温度减小。

峰值电子数密度随高度的减小先增大后减小， 且在高度29km 处取得极大值。

2.2 飞行速度

分 别 选 取 飞 行 速 度 6232m/s、5500m/s、4500m/s、3000m/s 对飞船周围等离子体分布进行仿真，得到电子数密度云图，如图8 所示。头部等离子体鞘套厚度及峰值电子数密度随飞行速度变化如图9 所示。

分析图8 和图9 可知， 飞行速度对航天器头部等离子体鞘套厚度及峰值电子数密度有明显影响效果。 四种速度对应的头部等离子体鞘套厚度分别为0.67m、0.69m、0.72m、0.82m。 飞行速度越小，鞘套厚度越大。

图8 不同飞行速度时电子数密度分布Fig.8 The electron number density distribution at different flight speeds

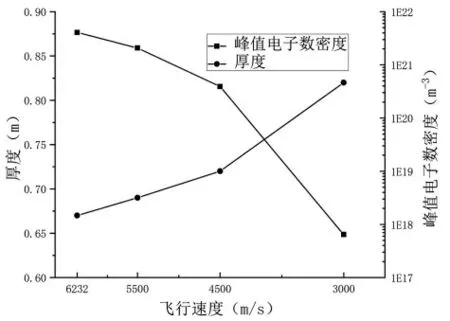
图9 厚度及峰值电子数密度随速度变化Fig.9 Thickness and peak electron density change with speed

四种速度对应的峰值电子数密度分别为4.07E21m-3、2.07E21m-3、3.91E20m-3、6.44E17m-3。 飞行速度越小，峰值电子数密度越小，全流场的电子数密度也越小。在飞行速度3000m/s 时， 航天器周围等离子体中几乎不存在足以影响到通信质量的等离子体密度。

在四种飞行速度下，电子数密度总是在航天器头部区域最大，随着身部往后逐渐变小，尾部会出现一小部分密度非常小的区域。

2.3 来流压强

分别选取来流压强139.04Pa，1390.4Pa 和13904Pa对飞船周围等离子体分布进行仿真， 得到电子数密度云图，如图10 所示。 头部等离子体鞘套厚度及峰值电子数密度随来流压强变化如图11 所示。

分析图10 和图11 可知， 来流压强对航天器头部等离子体鞘套厚度及峰值电子数密度有明显影响效果。 三种来流压强对应的头部等离子体鞘套厚度分别为0.59m、0.67m、0.74m。 来流压强越大，鞘套厚度越大。

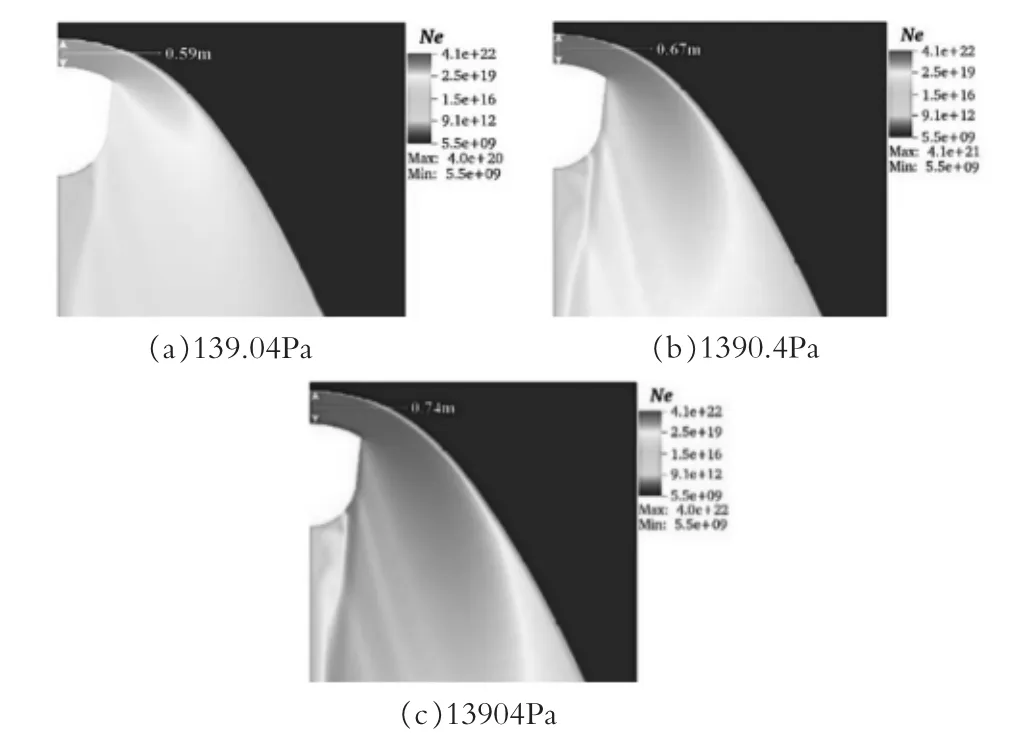
图10 不同来流压强时电子数密度分布Fig.10 The electron number density distribution at different incoming pressures

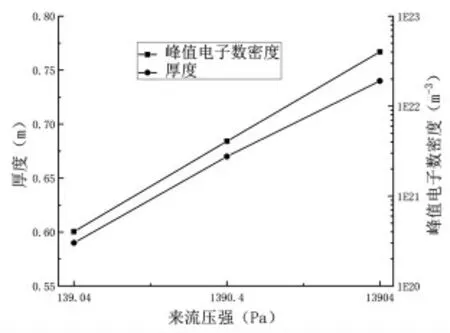
图11 厚度及峰值电子数密度随来流压强变化Fig.11 Thickness and peak electron density change with pressure

三种来流压强对应的峰值电子数密度分 别 为 4.02E20m-3、4.07E21m-3、4.01E22m-3。来流压强越大，峰值电子数密度越大，全流场的电子数密度也越大。

2.4 航天器构型

航天器构型分别为飞船、航天飞机和乘波体。其中飞船头部半径为1.25m，航天飞机头部半径为0.1m，乘波体头部半径趋近于零。

航天飞机和乘波体的网格划分如图12 所示。

图12 航天飞机和乘波体网格划分Fig.12 Grid division of space shuttle and waverider

对三种航天器周围等离子体分布进行仿真， 分别得到电子数密度云图，如图13 所示。 头部等离子体鞘套厚度及峰值电子数密度随航天器构型变化如图14 所示。

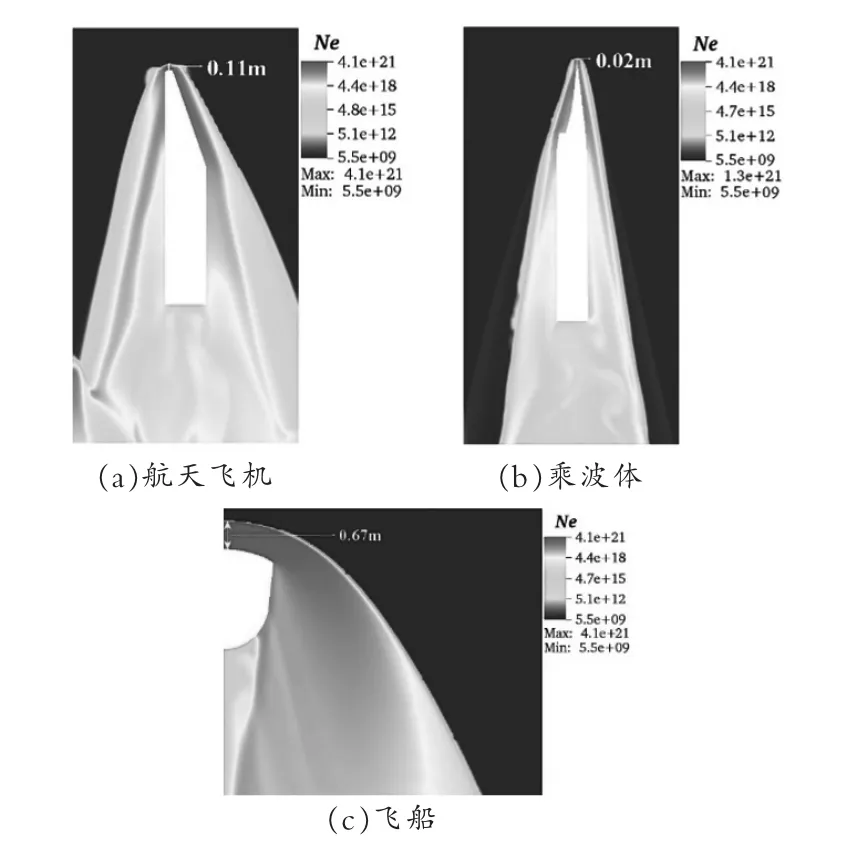
图13 不同航天器构型时电子数密度分布Fig.13 The electron number density distribution for different aircraft configurations

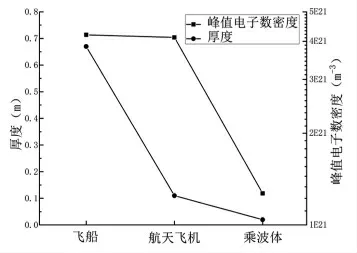
图14 厚度及峰值电子数密度随航天器构型变化Fig.14 Thickness and peak electron density change with aircraft configuration

分析图13 和图14 可知，航天器构型对航天器头部等离子体鞘套厚度及峰值电子数密度有明显影响效果。 三种构型对应的头部等离子体鞘套厚度分别为0.67m、0.11m、0.02m。 航天器头部半径越小，鞘套厚度越小。

三种构型对应的峰值电子数密度分别为4.14E21m-3、4.06E21m-3、1.27E21m-3。 航天器头部半径越小，峰值电子数密度越小，全流场的电子数密度也越小。

构型对航天器周围的等离子体电子数密度分布的影响效果具体有以下几点：

（1）对于飞船这样的钝锥构型，在头部区域电子数密度很大，且范围很广。往后部的过渡中，电子数密度衰减梯度较小，降低约1～2 个量级。

（2）对于航天飞机和乘波体这样的尖锐构型，在头部区域电子数密度很大，但范围很小。 往后部的过渡中，电子数密度衰减梯度较大，降低约3～4 个量级。

3 结论

通过对再入航天器周围等离子体分布进行建模和仿真，得到等离子体电子数密度分布。分析了不同飞行高度对等离子体压强、温度和电子数密度的影响，不同飞行速度、 来流压强和航天器构型对航天器头部等离子体鞘套厚度及峰值电子数密度有明显影响效果。

（1）在71.6～21.3km 的高度范围内，峰值压强随高度的减小而增大。峰值温度随高度的减小而减小。峰值电子数密度随高度的减小先增大后减小，且在高度29km 处取得极大值。

（2）飞行速度越小，鞘套厚度越大，峰值电子数密度越小，全流场的电子数密度也越小。

（3）来流压强越大，鞘套厚度越大，峰值电子数密度越大，全流场的电子数密度也越大。

（4）航天器头部半径越小，鞘套厚度越小，峰值电子数密度越小，全流场的电子数密度也越小。