基于BP神经网络数字识别技术的研究

王永亮

(山西大同大学浑源师范分校，山西 浑源 037400)

0 引言

阿拉伯数字作为唯一一种世界各国的通用符号，为每个国家每个地区的研究人员提供了发挥智慧的平台，使他们在数据的搜集以及处理等方面更加方便快捷，促进各国合作，进行更深刻的理论研究。并且，它在许多方面都有着广泛的实践作用，例如：统计数据的报告，金融方面的报表，对信封上邮编的识别，对车牌号码的精确识别等方面[1-3]。先前不少学者已经对神经网络做了大量的研讨，BP神经网络也因此而备受青睐。人们调查其系统实时性，研究其识别效果，更改其初始的权值以加快其收敛速度，探索最佳隐层节点数以提高网络，利用BP网络的优势正确地识别数字[4-8]。

论文主要分析的是BP(Back Propagation)神经网络运用于数字识别中处理问题的能力效果。研究其训练网络所用参数，进行分析比对，选用最合适、效果最好的参数进行最终测试，通过MATLAB这个强大的实验平台，对实验过程进行真实仿造和还原，从而验证BP网络运用于数字识别的可行性与有效性。

1 BP神经网络在数字识别中的应用

1.1 数字识别

数字识别是字符识别的一种，这里主要是运用BP神经网络对0，1，2，3，4，5，6，7，8，9这十个阿拉伯数字进行精确的识别。

数字识别通常都会分为好几个过程，以便按部就班地进行，减少差错和失误，而数字识别在神经网络中的进程大致分为数字输入、预处理、特征提取、模式匹配、判决、识别6个过程。

1.2 问题描述

设计一个适当的BP神经网络，要求可以正确识别10个阿拉伯数字，当它们在受到一定的噪声干扰影响时，也可以较好地进行识别。

1.3 模型建立

1.3.1 BP神经网络的创建

利用newff函数生成BP神经网络，此函数存在新旧两个版本，这里采用的是新版本，若直接使用会导致识别率偏低，并且与旧版本所得效果相差较大。造成此问题的原因是因为新版本中的神经网络函数把训练集分成了3份，即训练集train set,验证集validation set和测试集test set，默认比例为6∶2∶2。

针对本次实验中BP网络构建，由于训练数据少，训练集必须要完全保留进行训练，否则训练的效果会出现很大的偏差。所以我们通过将网络的divideFcn属性置空，达到高精度实验效果。

1) 构建网络传输函数的选用

三层网络结构，只涉及隐含层与输出层的传输函数。一般的，隐含层选用tansig和logsig函数，输出层选用tansig和purelin函数，此处比较时训练函数选用默认函数。不同传递函数对识别效果的影响如表1所示。

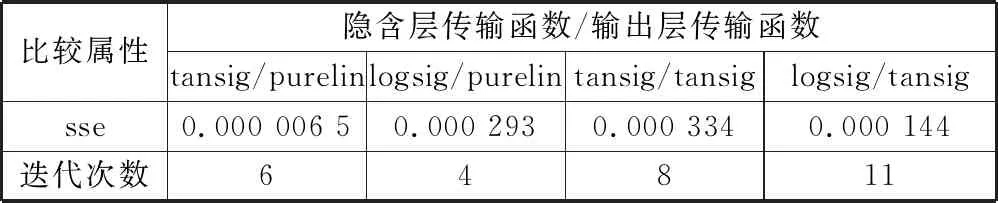
表1 隐含层与输出层不同函数比较

经比较得出，隐含层使用tansig函数，输出层使用purelin函数可以得到较好效果。

2) 构建网络训练函数的选用

训练函数通常包含以下几种：动态自适应学习率下降函数(traingda)，L_M训练函数(trainlm)，动量反传和动态自适应梯度下降训练函数(traindx)，梯度下降训练函数(traingd)，动量反传梯度下降函数(traingdm)。不同训练函数对识别效果的影响如表2所示。

表2 不同训练函数对误差识别率的影响比较

经过比较得出结论：使用traingda训练函数可以得到最佳结果。

1.3.2 BP神经网络的训练和仿真

BP神经网络构建完成之后，接下来要用样本数据对其进行训练，在此要注意所用的样本数据必须是合理的。最好使用理想样本和加噪样本相结合的数据。一般情况下，使用train函数来实施训练，使用sim函数进行仿真。

1.3.3 总体设计步骤

设计BP人工神经网络共分五步。

1) 输入输出设计——设计数字点阵(0～9)

以数字9为例，剩余数字不再一一列举。

{1 1 1 1 1

1 0 0 0 1

1 0 0 0 1

1 1 1 1 1

0 0 0 0 1

0 0 0 0 1

1 1 1 1 1}

2) 创建BP网络

确定好网络结构，设定好满足要求的网络输入、输出，就可运用MATLAB自带的神经网络工具箱中的函数创建训练网络。

3) 产生带噪声的数字点阵

在原有数字点阵的基础上，使用随机函数对数字点阵加噪。

4) 数字识别测试

当含有指定噪声的数字点阵进入到之前已经训练好的BP人工神经网络中时，页面会显示出它的识别结果，由于网络之前经过了训练，所以往往误差极小。

5) 结果分析

对最终测试的结果进行比较分析，从而验证BP网络用于数字识别的可行性与有效性。

2 在MATLAB环境下实现数字识别

以BP神经网络理论为基础，通过使用MATLAB神经网络工具箱中提供的函数，实现数字识别。

2.1 实验中使用的MATLAB函数

2.1.1 BP神经网络建立网络对象函数

net=newff(P,T,S,{TF1,...,TFN},BTF)

其相关参数的含义如表3所示。

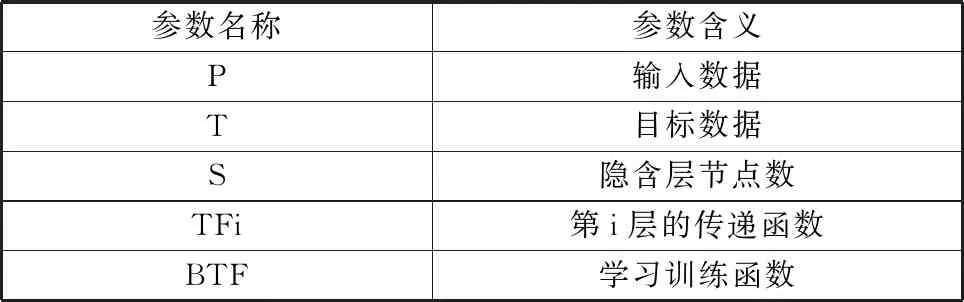
表3 BP神经网络建立网络对象函数相关参数

2.1.2 神经网络的训练函数

[net,train]=train(net,P,T)

其相关参数的含义如表4所示。

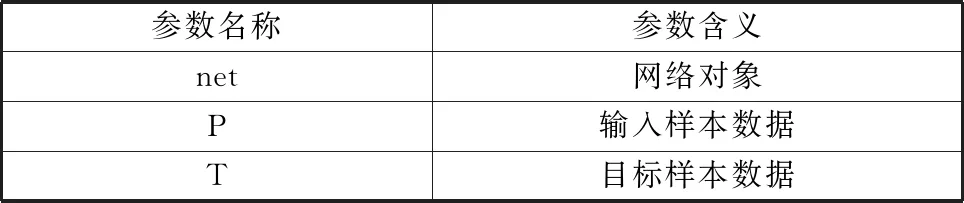
表4 神经网络的训练函数相关参数

2.1.3 神经网络的仿真函数

Y=sin(net,P)

其相关参数的含义如表5所示。

表5 神经网络的仿真函数相关参数

2.2 建立网络

在确定输入样本以及函数基本参数后利用newff函数训练建立神经网络。

2.3 产生带噪声的数字点阵

为了使结果不具有偶然性，这里采用产生随机数的方法来更改点阵进行加噪。例如对3和9进行加噪，这其中，噪声强弱是可变的。其余数字方法类似在此不做列举。

2.4 数字识别性能测试

使用上百个具有不同强度噪声的数字点阵测试网络的可靠性，通过plot函数直观呈现网络识别效果，从而验证识别网络系统的识别性能。

2.5 结果分析

利用工具箱中的函数，让带有噪声的数字点阵作为输入进入到构建好的网络中，之后对其进行识别和分析。这里用数字3和9举例说明，其他数字方法与此相类似，用BP学习算法进行训练，经过多次迭代计算后得到趋于精度值的预测曲线，得出误识率与噪声方差的关系，然后对数字进行识别。

经过训练后的BP神经网络误差曲线如图1所示。

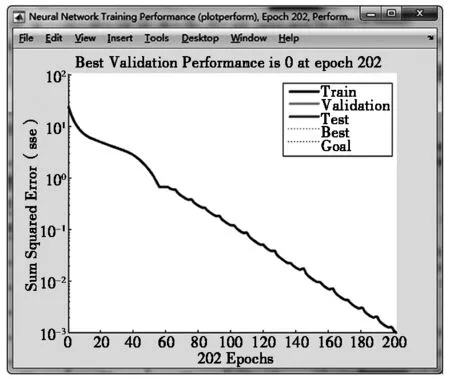
图1 训练误差曲线图

图1可以看出，采用BP学习算法所获得的训练误差曲线中，在经过202次迭代计算后，训练曲线逐渐趋于预期的精度值0.001。

噪声的均值为0，和方差则是从0到0.5以0.05的间隔，采用这样的模型来进行系统仿真。

现在对已设计好的网络输入任意加有不同强度噪声的数字点阵，在原有理想训练样本的基础上，产生100组含有该类型的样本，之后进行仿真实验。根据仿真结果计算出这100组样本的误识率，得到网络误识率与噪声强度的变化曲线如图2所示。

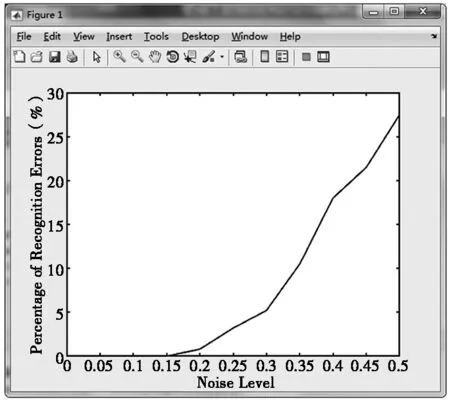
图2 误识率与噪声强度的变化关系图

图2中，实线所代表的是经过了理想样本训练的网络对数字识别的误识率的变化。根据图2我们可以看出，随着噪声和方差的逐步变大，网络的误识率呈现出一步步上升的趋势，噪声方差低于0.15时误识率为零，可以完全正确识别。在噪声方差低于0.3之前，网络误识率是很小的，基本可以实现数字的正确识别。

用已设计好的神经网络对含有噪声的数字9进行识别。含有噪声的数字9的点阵如图3所示，经过神经网络识别过后数字9的识别结果如图4所示。

从图3和图4分析可以看出，对网络进行生成与训练、仿真后，训练后的神经网络正确地识别出了数字9。

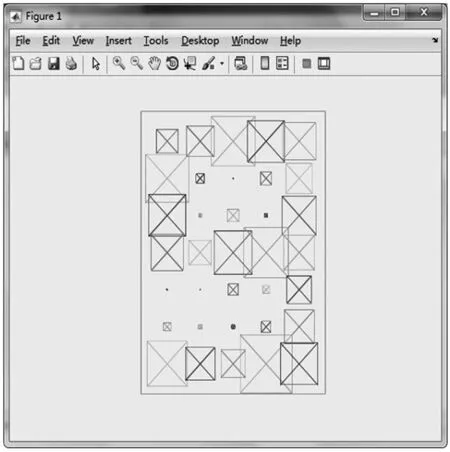
图3 含有噪声的数字9的位图

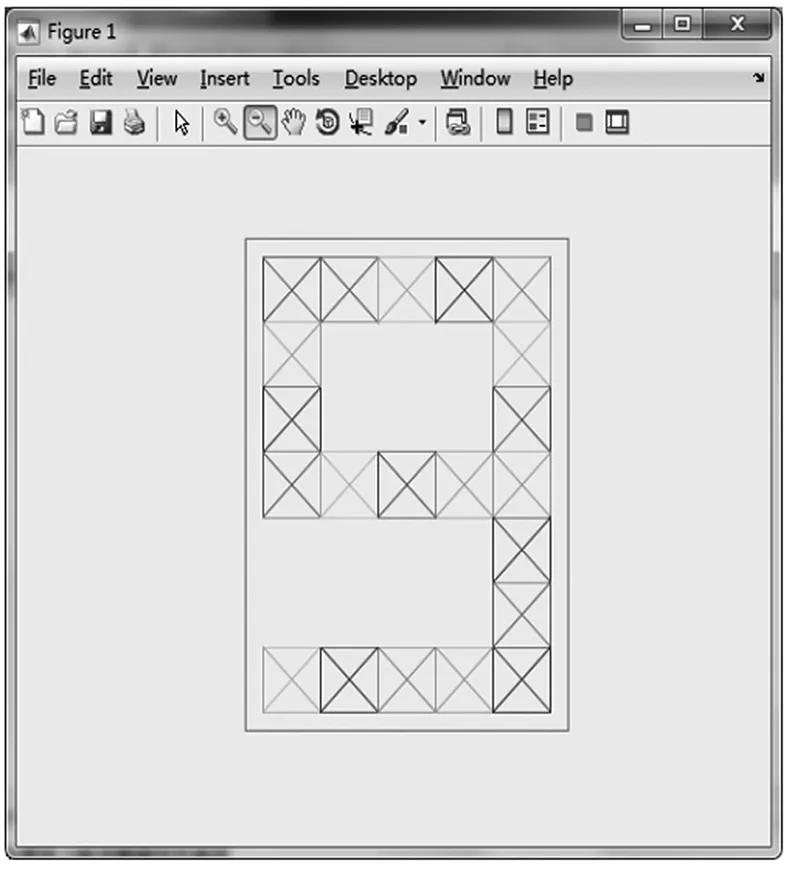
图4 识别结果

3 结束语

利用BP神经网络的识别能力，将BP神经网络运用到一个实例中，识别了包含不同噪声的数字0到9，并且针对不同噪声强度的样本进行仿真。之后的仿真结果充分表明，BP神经网络在噪声强度小于0.3的时候是可以正确地识别出数字的，另外只要不断地调整仿真的迭代步数是能够有效提高网络的容错能力的。