基于模型预测控制的逻辑动态管理策略*

范艺凡，杨惺幸，董守鸿，潘天泽

(河南科技大学信息工程学院，河南 洛阳 471009)

0 引言

混合动力汽车最关键的技术就是整车控制策略，不同的方式对整车动力性能和节能性有不同影响。为了提高设计质量，缩短研制周期，在设计阶段就需要根据有关设计参数，对汽车动力性和燃料经济性进行预测[1]。

本文针对一种并联混合动力新能源汽车，基于贝叶斯推论对未来可能加载与车轮的功率需求进行了预测，进而基于模型预测控制设计了控制策略，优化计算出使得燃油消耗最小情况下驱动车辆的电机转矩控制变量。

1 并联混动汽车工作模式分析

并联新能源传动系统主要包括：发动机，发电机，动力耦合机构和变速机构。

该并联新能源汽车具有六种驱动方式。离合器的状态与驱动模式状况如表1所示。

表1 驱动模式与离合器状态

2 功率需求预测

为了预先获取驱动车辆的目标需求功率，采用离线实验对油门开度、某一负载下发动机转速等输入变量进行数据统计，构建输入范围内需求功率的概率数据查找表对未来的目标需求功率进行预测。

选取转速ω,未来需求功率Preq和油门开度α构成控制变量ui，把ui中的变量在最大值和最小值之间进行离散化得Ψhj，通过实验测得ui的取值集合Φ(k)，就可以通过贝叶斯概率推论计算需求功率集合Ψ1j下的后验概率[2-4]。

功率预测的方法如图1所示。

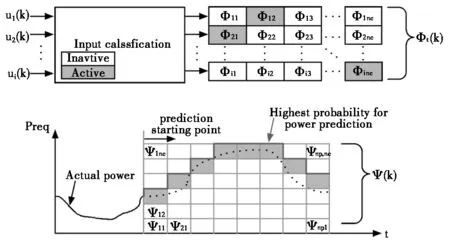
图1 需求功率预测方法

训练数据记录5个小时内的车轮加载，输入变量选取为：λi=[α ω Preq]，为保证精度，这里α的离散为5个级别：30%，40%，50%，60%，70%，ω离散为5个级别(300rpm-2 300rpm)，Preq离散的数值nc=25。测得的需求功率转矩和预测的功率转矩记录如图2所示。由图2可见，基本贝叶斯后验概率的功率预测方法具有较高预测精度。

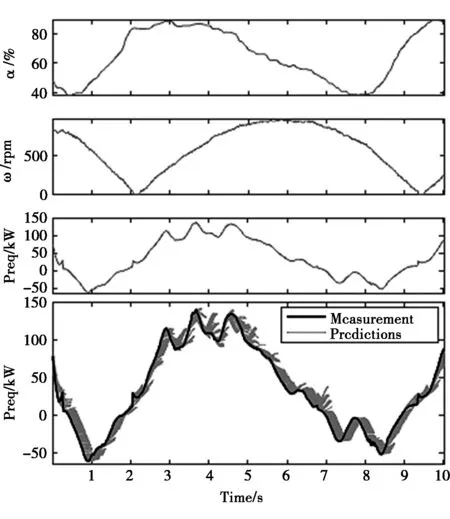
图2 功率需求预测结果

3 模型预测控制策略

目标需求转矩通过功率需求预测获得，模型预测控制取电机输出转矩u(k)作为控制变量，取SOC作为状态变量。优化控制变量序列u(k)通过预测模型控制策略求解最小燃油消耗获得，序列中的第一个值用来进行当前时刻混动汽车的控制。

4 模型的优化方式

4.1 MPC优化模型

通过对并联新能源车辆的驱动模式分析，设计基于驱动模式切换的MPC模型预测控制策略。状态变量的转换和燃油消耗如公式(1)所描述：

(1)

式中，x(k)是时刻k时的SOC值；y(k)是时刻k时的总燃油消耗；δ(k)是时刻k时驱动模式矩阵；u(k)代表电机输出转矩Tm(k)的控制变量。根据实际的驱动模式，A为一个1×6的矩阵：

A=[μi(k)ηbat(k)/Qc0μi(k)ηbat(k)/Qcμi(k)ηbat(k)/Qcμi(k)ηbat(k)/Qc0].

同样B1和B2也分别是1×6的矩阵，用来计算总的等效燃油消耗：

B1=[0a1(k)(Treq(k))+a0(k)a1(k)(Treq(k))+a0(k)a1(k)(Treq(k))+a0(k) 0 0]

a0和a1是发动机燃油消耗拟合系数。混动汽车每一时刻只能以六种驱动模式中的一种运行，为了在模型预测控制中体现驱动模式，定义δ(k)为：δ(k)=[δ1δ2δ3δ4δ5δ6]T，矩阵中的每一项在时刻k只可能有一项是1，而其它值都是0。如果δ1是1，其余都为0，意味着车辆工作在发动机单独驱动模式。对公式(1)进行滚动优化，优化模型描述为：

(2)

公式中，N为预测时域区间；xmin(k)和xmax(k)是SOC的上下限值；C1,C2,C3和C4是从公式中得到的优化参数。

4.2 MPC模型求解

模型预测控制采用Matlab中的Gurobi优化工具处理。在时刻k，控制变量序列u(k)在预测区间(k-k+N)进行计算，每次只有控制序列的第一个值被模型预测控制策略用来分配电机转矩，利用前述优化方法重复上述步骤，会得到k+1时刻的控制序列。为了降低模型预测控制策略的计算复杂度，提高模型预测控制的实时效率，驱动模式切换过程中需要进行电机转矩的判定规则。目标需求转矩Treq可以用来判定车辆是否是制动或是停止，当Treq小于或等于0时，意味着车辆处于再生制动状态或是静止状态，电机输出转矩可以直接确定，当Treq大于发动机的最大输出功率时，车辆工作在混动模式，除此之外，车辆应在其它四种驱动模式之间切换，电机输出转矩可通过优化目标函数得以确定。

5 仿真实验及结果分析

驱动系统主要包含一台57 kW的发动机和一台50 kW，最大输出扭矩为272 N·m的电机,车辆最大需求目标转矩为650 N·m，车辆其它参数如表2所示。

表2 混动汽车参数

ADVISOR用来进行仿真，SOC的初始值设为0.7，上限值设为0.8，下限值设为0.3，预测区间时长设为15 s，采样间隔设为1 s。循环工况如图3(a)所示，模型预测控制和CD-CS控制下的SOC结果对比如图3(b)所示，燃油消耗的对比如图3(c)所示。

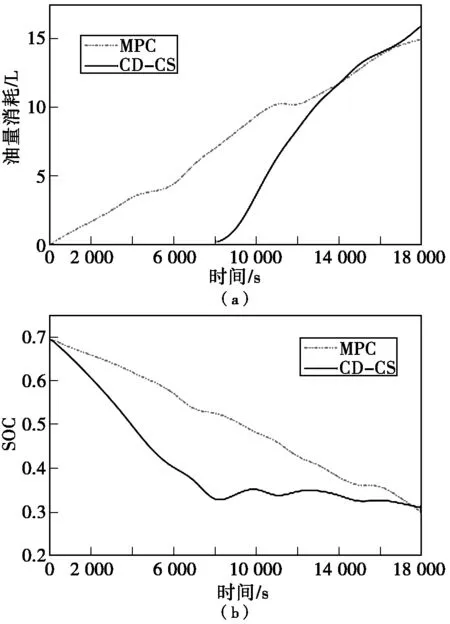
图3 循环工况SOC和燃油消耗的比较

由图3(b)可以看出，CD-CS控制时,在8 000 s的时候，电池的SOC会降到0.3左右，而后电池的SOC就维持在0.3左右。在MPC控制时，电池能量是逐步消耗的，至工况结束时，电池的SOC值为0.347。由图3(c)可以看到，CD-CS在开始的8 000 s，是基本上采用电池驱动，而后燃油的消耗迅速增加，整个过程中燃油的消耗量为14.75 L，而MPC的燃油消耗是逐步上升的，整个过程中的燃油消耗为13.04 L。由此可见，相比于CD-CS控制，MPC更有效合理的使用了电池的能量，燃油的消耗可以降低13%左右。

并联式混合动力汽车改善汽车经济性的核心就是改善发动机的工作点[5]。两种控制策略下发动机的工作点如图4、图5所示。可以看到，CD-CS控制下，发动机的工作点分布分散，而MPC控制下发动机的工作点分布相对集中。意味着MPC控制下，发动机更有效的工作在高效区域，这也是有效提高燃油经济性的原因。

图4 CD-CS控制下的发动机的工作点

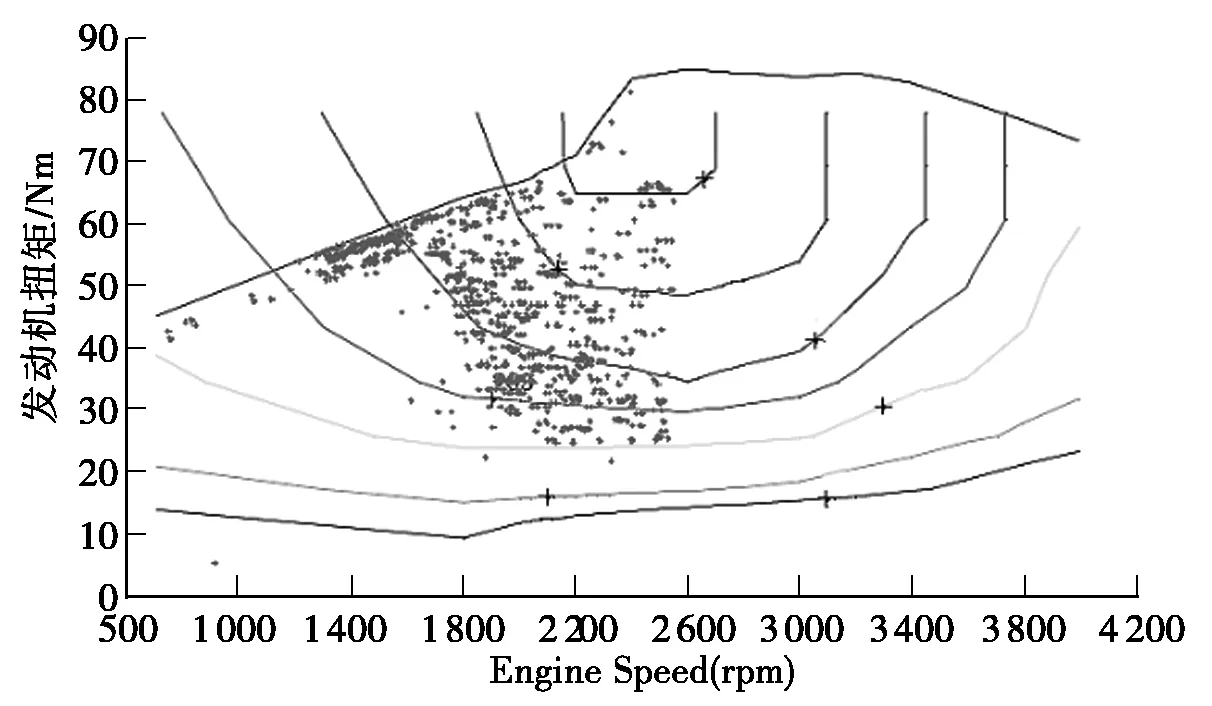
图5 MPC控制下发动机的工作点

为了进一步验证MPC在提高燃油经济性上的性能，选择另外两种工况循环(NEDC和NYCC)加以验证。CD-CS控制下和MPC控制下的燃油消耗进行比较。NEDC工况下，MPC控制时的燃油经济性提高了10.07%，NYCC工况下MPC控制时的燃油经济性提高了13.07%。NYCC工况下的燃油经济性好于NEDC的原因是,NEDC工况下车辆速度相对于NYCC的变化较少。

6 结论

本文提出了一种基于模型动态预测控制的逻辑动态并联混动汽车管理策略。基于贝叶斯推论，设计了系统燃油经济性最优的模型预测控制策略。仿真结果表明，该模型预测控制策略能够实时进行燃油经济性最优控制并能通过查找表的方式实时运算，避免电池的过度使用，有效的提高系统的燃油经济性。