基于非线性自回归模型的矿井粉尘浓度预测

周旭，王艺博，朱毅，秦思佳

(1.华北理工大学 理学院，河北 唐山 063210；2.华北理工大学 以升创新教育基地，河北 唐山 063210)

引言

煤炭在我国能源结构中占有着绝对重要的地位，在工业化建设初期曾占到能源结构总量的90%。随着近几十年来对油田的开采，煤炭在能源结构中的占比才有了一定程度的下降，但仍在能源结构中占有主要地位。可以预见，煤炭工业在国家能源结构以及国民基础经济中的地位是不可代替的，具有长期性和稳固性。随着煤矿机械化水平的提高，矿井粉尘不断增加。在矿井事故中，大多数事故都与矿井中的粉尘浓度有关。矿井粉尘不仅会危害地下工人的身体，而且当粉尘达到一定浓度时会引起爆炸，甚至会造成更严重的地下灾害[1]。因此，矿井防尘工作越来越重要，准确预测矿尘浓度对矿井安全生产具有重要意义。

相关文献表明，学者们主要采用神经网络模型对粉尘浓度进行预测，如：改进的神经网络模型[2]、BP神经网络模型[3]、熵权法RBF神经网络[4]。王永斌等[5]建立的灰色-广义回归神经网络组合模型以及基于费舍尔得分和支持顺序前向搜索算法[6]的支持向量积模型，研究该模型对尘肺病预测的准确性。上述模型虽然在传统的拟合预测领域中表现出了较高的拟合度与准确性，但由于模型中存在的遗忘机制，导致其对具有时序特征数据的预测会有一定的偏差。因此，结合神经网络模型的预测能力，以及时间序列模型对时序型数据的处理能力，构建模型对矿井粉尘浓度进行预测无疑是一种有效的预测方法。但传统的神经网络模型，在数据量较小，且样本数据受到多方面因素影响时，很难展现出良好的性能。而传统的时间序列模型，虽然对时间变量作为自变量的数据样本具有良好的拟合效果，但是在进行预测时，只能做到短期的预测，且误差急速增长。

为了解决这些问题，该项研究融合时间序列与神经网络的模型，提出一种非线性自回归的矿井粉尘浓度预测模型，多重考虑了变量时间因素以及模型输出结果对模型本身的影响。

1模型理论基础

1.1 时间序列

时间序列的建模及预测在学术界和实际应用领域极为普遍，如城市交通量、人口增长量、股市价格、国民收入、太阳黑子数等预测问题[7]。自1970年问世以来，逐渐形成了一整套时间序列识别、估计、建模、预测及控制的理论和方法。以Box-Jenkins为代表的现代时间序列预测方法建立在随机过程理论基础上，具有结构简单、建模速度快、预测精度高等优点，并且解决了非平稳序列时间序列的处理问题，非常适合现实生活中各类随机性强的时间序列的分析和预测[7]。

一般来说，建立ARIMA模型有3个阶段，分别是模型识别和定阶、参数估计和模型检验。其中模型识别指在绘出时序图后，判断所需差分阶数，并由ACF与PACF图判断 与 的取值，其原始时间序列模型为：

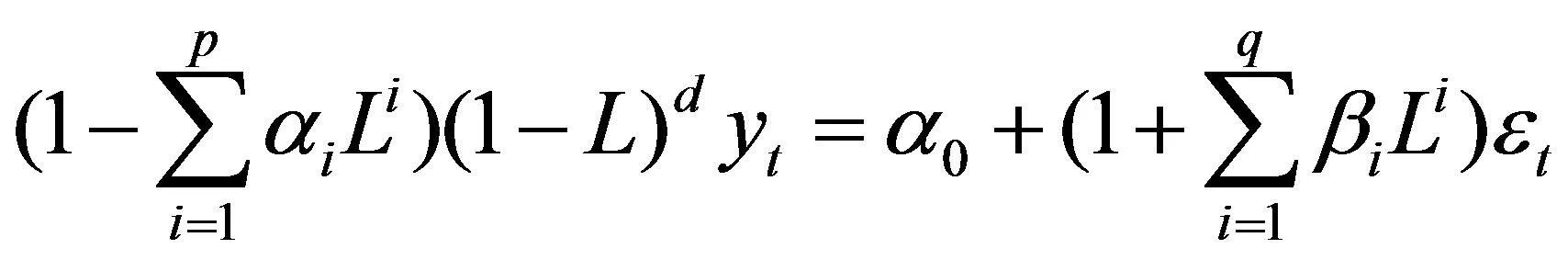
(1)

其中L为y的滞后算子，其满足：

(2)

模型检验指根据所计算得到的模型残差值对其进行检验，判断模型反应序列变化的完整性。

1.2 神经网络理论基础

神经网络法的学习和训练过程包括正向传播和反向传播2个阶段。在正向传播过程中，样本数据通过隐藏层的传递函数从输入层传递到输出层[8]。如果输出层没有得到所需的输出，则进入反向传播过程，沿原正向传播路径返回误差信号，采用均方误差和梯度下降法修改网络连接权重，调整网络实际输出与引导学习信号之间的均方误差值。重复此过程，直到达到指定的错误要求或达到最大培训次数为止。图1所示为神经网络模型的基本原理。

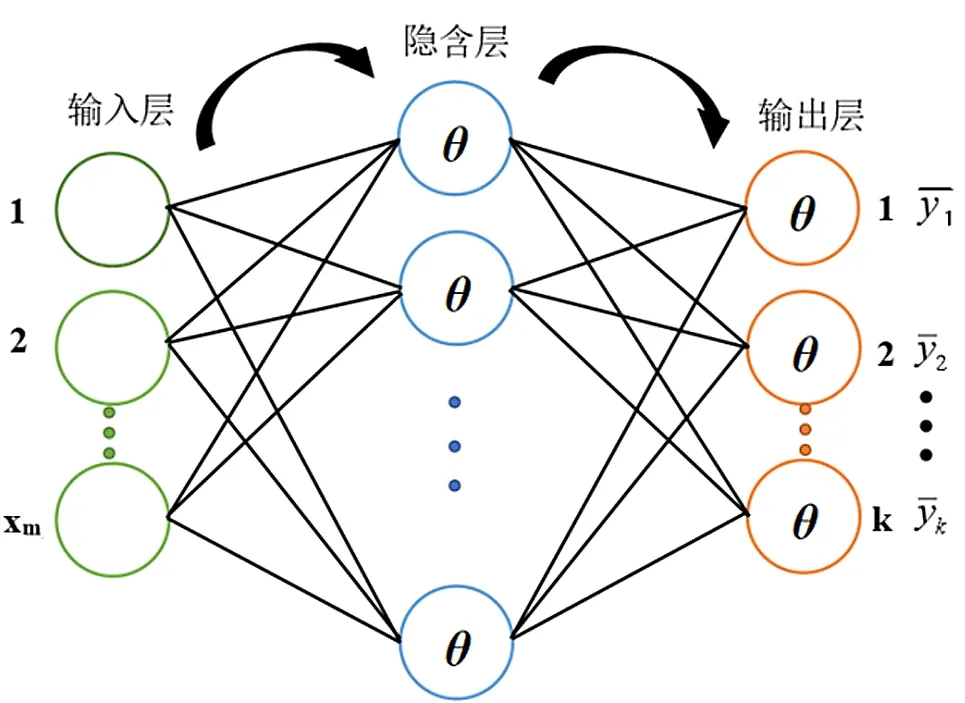
图1 神经网络原理图

考虑到变量与样本在训练过程中所受到的综合影响因素，输入集数据不单会受到观测值变量的影响，还会在一定程度上受到输出数据的影响，因此需要在输入与输出数据之间建立影响选用外因(外部)输入非线性自回归NARX模型对数据集进行处理。

2基于时间序列神经网络模型对矿井中粉尘浓度的预测

2.1 原始数据准备与处理

以某矿5424工作面粉尘浓度为原始数据来源[9]，通过采集筛选时间在某日9:31～10:17之间的47组数据，建立合适的时间序列神经网络模型，在模型检验通过后，将其用于预测10:18至10:21这4个时间点的粉尘浓度，进而验证模型的适用性。表1所示为工作面在筛选时间内的对应粉尘浓度。

表1 原始数据

将表1中的时间与其所对应的粉尘浓度导入SPSS后，将其对应时间的变量进行初始化，得到定义出的时间变量并将其绘制成如图2所示时序图：

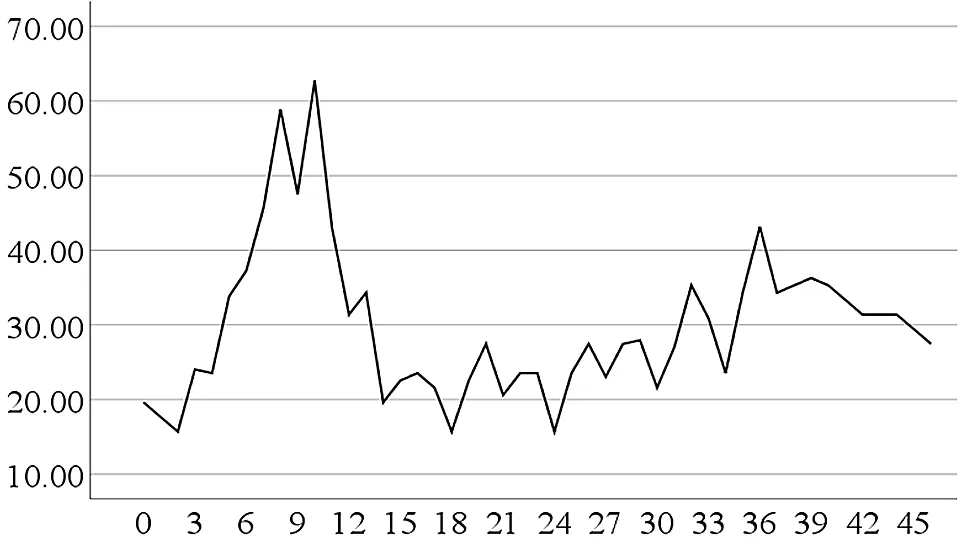
图2 粉尘浓度时序图

从图2中所反映的粉尘浓度变化趋势来看，时间因素在粉尘浓度变化的影响因素中占有极大的权重，且其浓度变化趋势与时间变量的关系并非简单的线性关系，因此采用神经网络模型对此变量进行预测。

2.2 时间序列神经网络模型的建立

(1)隐藏层层数的确定

隐藏层负责处理输入特征的信息，具有一个隐含层的网络可被称之为单隐含层网络，具有两个及以上隐藏层的网络可被称之为多隐含层网络，用于解决复杂问题。网络层数增多，会提升运算的精度[10]。但模型的复杂程度也随之提升，且过拟合风险也会变大。若为简单问题，一般选取单隐含层网络，对于复杂问题一般可设置多层网络。考虑到实际数据样本量较少，不易发生过拟合的现象，并为了提高模型预测结果的拟合度，该项研究选择10层网络以及2个延时来构建模型。

(2)激活函数的选择

由于神经网络能够不断学习的本质就是在接收不断训练误差的反馈中，来优化自身的模型参数。其中，当前层的误差大小与激活函数的选择有着密切关系[11]。由于sigmoid 函数与tanh函数的导数值均不大于1，在迭代的过程中必然会出现梯度消失的情况，导致训练提前终止。而ReLU函数则可以很好地避免这一现象的发生，只要采用其导数值为1的神经元进行学习，就能有效地规避梯度消失的问题，因此选用ReLU函数作为该研究模型的激活函数。

(3)训练算法的选取

在神经网络训练的过程中，选用Levenberg-Marquardt、贝叶斯正则化和量化共轭梯度3种算法进行训练。对于大多数问题，推荐使用Levenberg-Marquardt，对于一些含噪声小的问题，贝叶斯正则化虽然需要更长的时间，但能获得更好的解。对于数据量比较大的问题，选取量化共轭梯度。因为它使用的梯度计算比其他2种算法使用的Jacobian矩阵计算更节省内存。由于该项目所使用的数据样本较少，不易出现过拟合的现象，同时也不会花费过多的训练时间。因此，为了追求更高的拟合度，该研究使用的是贝叶斯正则化的训练方式。

2.3 模型检验

2.3.1误差自相关检验

误差自相关是对误差(观测值与预测值的差值)进行自相关计算，通过观察误差自相关曲线可以判断预测模型是否能够准确预测结果的趋势性、季节性、随机性。误差自相关是一个检测性的指标，需要在预测模型构建并计算出预测值后计算来对其进行评估。对于完美模型，自相关函数只有一个非零值，并在零滞后时出现。如果预测误差中存在显著相关关系，则需对预测结果进行改进，误差自相关系数的计算公式如下：

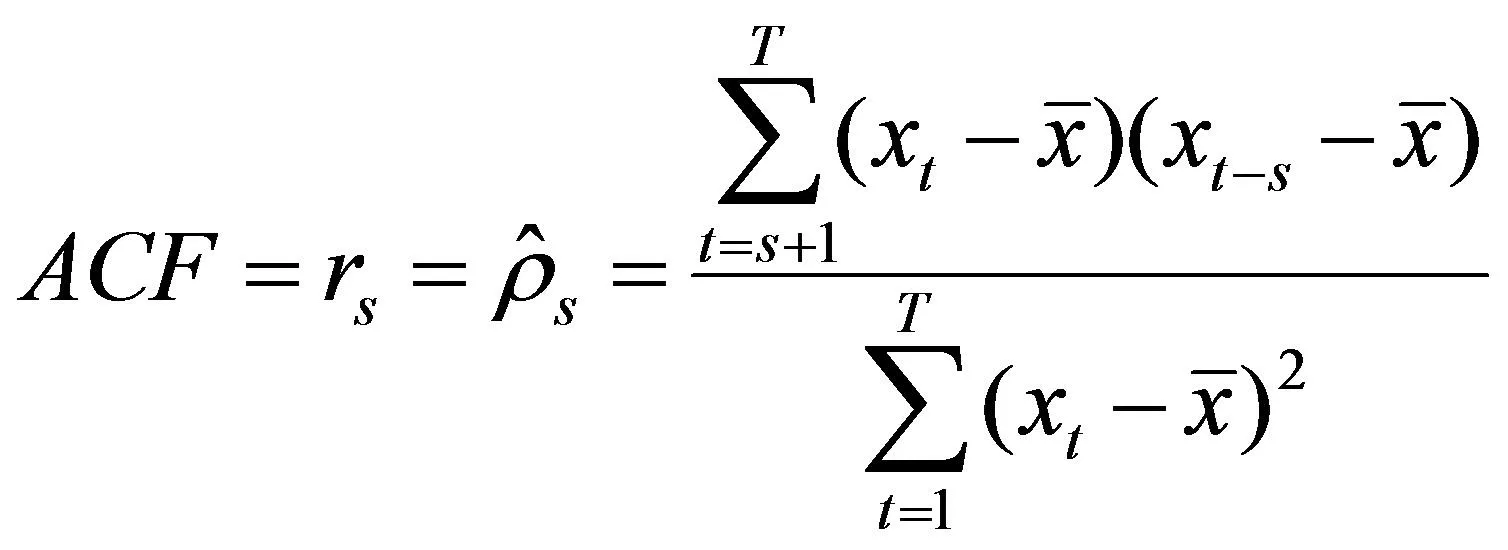
(3)

图3是该项研究模型成果所表现出来的误差自相关系数：

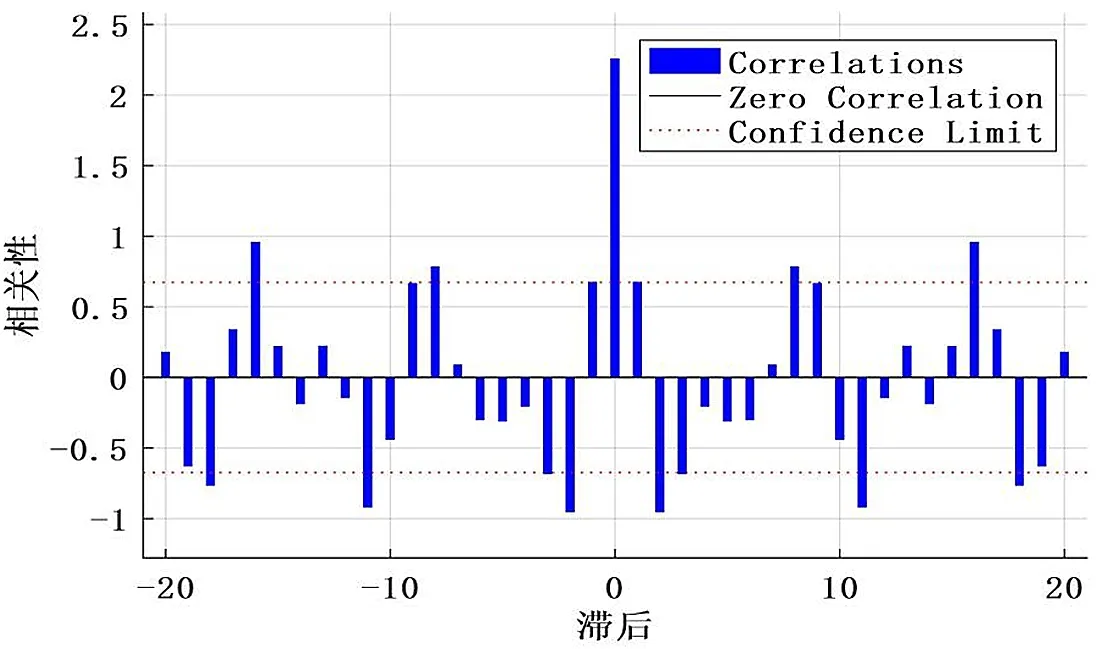
图3 误差自相关

由图3所示的误差自相关系数可以看出，除了零滞后时的1以外，其余区间的模型置信度均在置信区间内，因此模型看上去是足够的。

2.3.2输入-误差互相关函数

输入-误差互相关函数说明误差如何与输入序列 相关。对于完美的预测模型，所有相关性都应为零。如果输入与误差相关，则应该可以改进预测，这可以通过增加抽头延迟线中的延迟数量来实现。在这种情况下，所有相关性都在零附近的置信边界范围内。图4是该项研究模型成果所表现出来的输入-误差互相关函数。

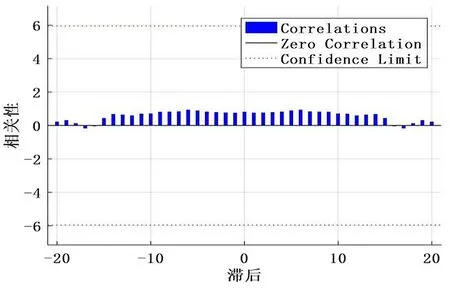
图4 输入-误差互相关函数

由图4可以看出，该项研究的模型结果中的输入-误差互相关函数的相关性，均在极大程度上收敛于零附近的置信边界范围内，因此可以证明该项研究的预测模型具有良好的预测效果。

2.3.3综合检验指标分析

图5所示为模型在迭代过程中，预测结果与真实结果间均化误差的变化。

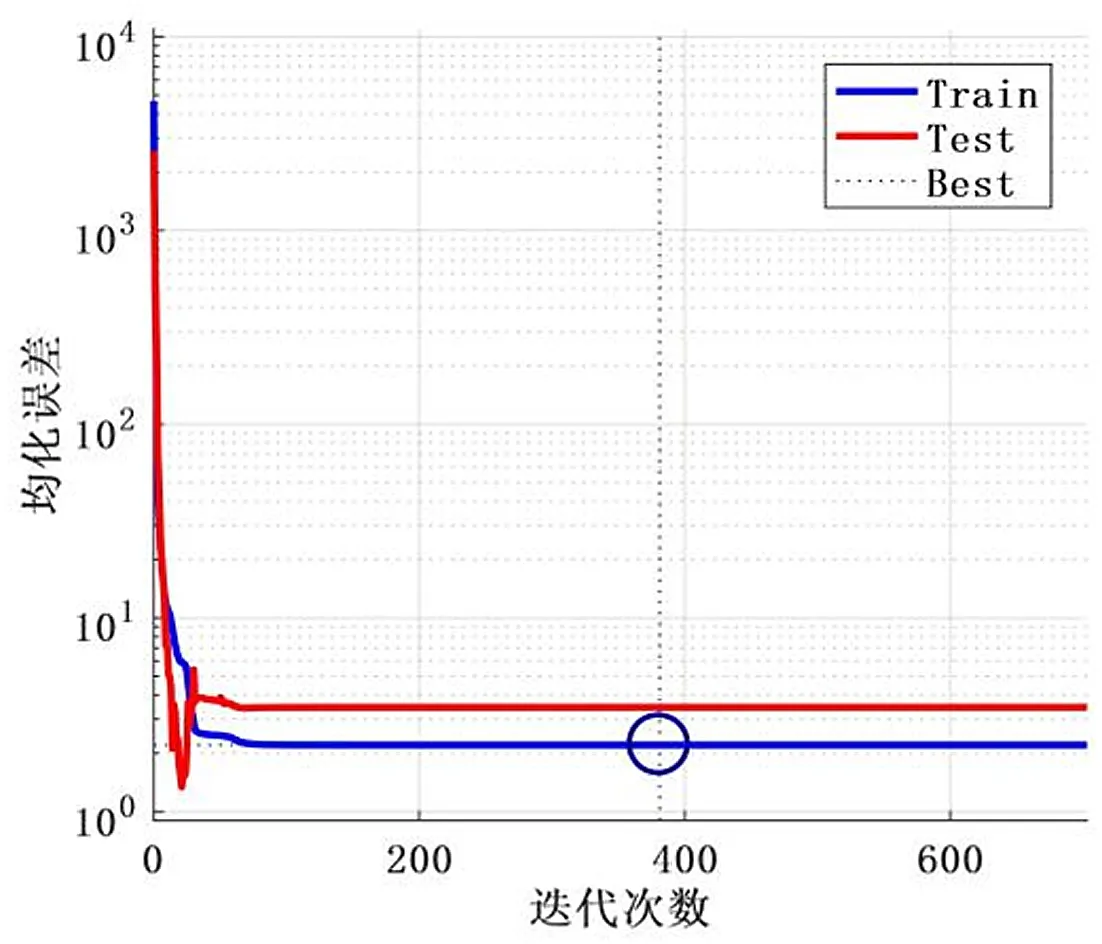
图5 模型均化误差

均化误差是指拟合结果的总误差值与拟合样本数的比值，代表的是预测结果的整体误差偏移；平稳R方指的是模型能解释因变量变化的百分比例，它表示的是预测模型与原数据样本的拟合程度[12]。由图中数据可知，所得到的预测函数，其均化误差达到了2.204 6的程度，等同于模型的误差在10%以内，同时不论是训练集还是测试集函数的平稳R方均在0.9以上，神经网络模型集和采用数据集的回归结果都在拟合曲线上，这表明该模型具有很好的拟合性。

2.4 模型预测

图6 所示为实际粉尘浓度以及TN预测模型对粉尘浓度的预测结果。

图6 拟合图像

利用模型对9:31至10:17期间的粉尘浓度进行拟合后，对10:18至10:21这3个时间点的粉尘浓度进行预测，预测结果如表2所示。

表2 模型预测结果

由表2可知，建立的时间序列神经网络模型对10:18至10:21的粉尘浓度预测结果呈下降趋势，这与所测得的实际值相符。同时，在之后的预测结果中，预测结果的误差值波动较小，因此该模型对粉尘浓度的长期预测具有一定可行性。

3模型对比

由于该模型是基于时间序列模型和神经网络模型所衍生出来的复合模型，因此在得出模型结果时，需对传统的模型预测结果进行比对分析，以确定复合模型是否具有良好的拟合性能和泛化性能[13]。图7所示为3种不同模型与原数据的拟合图像对比图。

图7 拟合图像对比图

其中，3个模型拟合综合结果的评价如表3所示。

表3 3个模型拟合结果的比对

由表3中的对比结果可以看出，外因输入非线性自回归模型(NARX模型)无论是在误差率还是预测函数的拟合效果上都要优于传统的2个模型。因此，相较于传统的2个模型，NARX模型能够更好地拟合样本数据的变化。

4结论

(1)由于影响矿井中粉尘浓度的因素较多，且实际情况更为复杂，因此仅时间变量作为单变量来对粉尘浓度进行预测，虽然预测结果的置信度符合要求，但预测结果仅具有参考性。

(2)在使用普通的BP神经网络对粉尘浓度进行预测时，由于其前馈的参量只有误差，很难反映输出结果对输入数据本身的影响。因此采用外因(外部)输入非线性自回归模型来对粉尘浓度进行预测，其预测误差率降至3.8%。

(3)外因输入非线性自回归模型(NARX模型)在对矿井内粉尘浓度的预测上，同时继承了时间序列模型对原数据的良好拟合度，以及神经网络模型较好的预测能力，并在原有基础上降低了一定预测时间内的整体误差，具有优越的拟合预测效果与泛化性能。