岭估计在似大地水准面精化中的应用

杨燕燕，王晓红

(华北理工大学 矿业工程学院，河北 唐山 063210)

GPS定位技术由于具有较高精度、成本低且作业便捷的特点，故在测绘领域得到广泛应用，并且随着GPS技术逐渐成熟，利用GPS定位技术与高精度似大地水准面模型，可以测定正常高[1]，实现对似大地水准面的精化。在实际工程测量中，采用GPS技术能够准确测定地物点的坐标，但其测定的高程为大地高，在实际工作中无法直接利用，需通过采用一定的方法将其转换成具有实际意义的正常高。因此，将大地高转换为实际所需的正常高是数据处理的关键，且高程异常拟合的精度直接影响坐标转换精度[2]。常用的GPS转换方法有高程拟合法，它是将GPS水准点获得的高程异常近似看作各点坐标的曲面函数，通过此拟合函数来计算其他地方的GPS点的高程异常，从而得到正常高[3]，高程拟合法只需要GPS测量数据和相应的水准测量数据，并选择合适的拟合模型和计算方法，简单、快捷，因此成为区域似大地水准面精化常用的一种方法[4]。

在实际测量工作中，由于大地水准面的复杂性，在进行多项式拟合时，往往需要较多的拟合系数，这就会使得拟合系数之间存在严重的多重共线性，即设计矩阵的病态性[5]。如果多项式曲面拟合模型出现病态性问题，将很难求解出准确的参数，根据该模型得到的高程异常值也会有较大误差。采用岭估计的有偏估计方法可以很好地解决此类方程病态性问题。

1区域似大地水准面精化

似大地水准面是指从地面点沿正常重力线量取正常高所得端点构成的封闭曲面，与地球椭球体、大地水准面一样，是获取地理空间信息的重要高程基准面之一[6]。大地高系统、正高系统和正常高系统分别以地球椭球面、大地水准面和似大地水准面为常用的参考基准面。某点的大地高是该点沿参考椭球面的法线到参考椭球面的距离；正高是地面点沿通过该点的铅垂线至大地水准面的距离；正常高是地面点沿通过该点的垂线方向到似大地水准面的距离[7]。在实际测量工程中，我国采用以似大地水准面为基准的正常高作为我国的高程系统，将正常高与大地高之间的差值称作高程异常值[8]。

精化似大地水准面常用的方法有重力法、GPS水准拟合法等。在不考虑地球重力场模型和重力等数据影响的情况下，在某小区域范围内，利用高精度的GPS大地高和精密几何水准数据通过最小二乘方法来拟合区域似大地水准面能得到良好的效果[9]。GPS水准法即高程拟合法，在实际应用中，大多采用多项式拟合的方法。

多项式曲面拟合法是将小范围GPS网内的似大地水准面视作不规则曲面，根据GPS实际测得的大地高和水准点求出其高程异常值[10]，通过相应的数学模型对测区的似大地水准面进行拟合，建立与该不规则曲面最接近的多项式曲面模型，根据此模型求解出待定点的高程异常值，然后利用GPS测得的大地高减去得到的高程异常值，即可求出待求点的正常高[11]。该项目以二次多项式拟合为例，介绍此数学模型以及理论基础。

二次多项式曲面拟合法数学模型为：

F(x,y)=a0+a1x+a2y+a3x2+a4y2+a5xy

(1)

其中，F(x,y)表示函数模型；(x，y)为观测点坐标；a0-a5为拟合系数。在进行二次多项式拟合时，拟合系数有6个，因此观测点的个数应不少于6个。其中，当观测点个数大于6时，可根据最小二乘法则vTpv=min求解拟合系数，假设观测点个数为n，由(1)式可列误差方程：

(2)

总误差方程式为：

V=BX-L

(3)

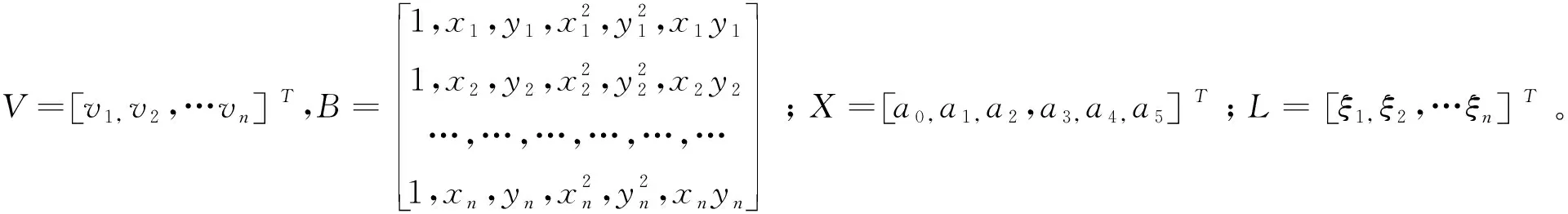
X=(BTB)-1BTL

(4)

得到系数矩阵后，将其带入公式(1)即可得到高程异常值。多项式函数理论上可以任意确定次数，理论上多项式的次数越高，拟合模型越接近真实曲面，但是在实际应用中，次数不断增高的同时，会造成法方程系数阵呈病态性，即拟合系数之间也出现多重共线性的情况，且系数越高，多重共线性越严重，从而使得高程拟合结果不准确。目前，采用岭估计的有偏估计方法可以很好地解决法方程病态性的问题。

3岭估计

岭估计方法是根据最小二乘估计提出的一种改进的有偏估计，它主要是通过确定一个很小岭参数k来使法方程系数阵N的一小部分特征根非常接近于零，从而打破系数阵的严重复共线性，进而消除或减弱数据呈病态性对参数估计的影响[12]。岭估计参数模型如式(5)：

XOR=(BTPB+kI)-1BTPL

(5)

由岭估计的性质可知岭估计是在最小二乘估计的基础上进行的改进，而其最重要的特点就是通过加入了岭参数k，以此来打破系数阵B的严重复共线性，所以使用岭估计最重要的就是确定岭参数k，因此众多学者做了大量的工作来进行探索，提出了很多方法来确定k值，但目前为止还没有一种公认的好方法[13]。目前，比较常用的2种方法就是岭迹法和双h法。

3.1 岭迹法

所谓岭迹法，就是以岭估计XOR的分量Xi(k)=(i=1,2,…t)作为岭参数k的函数，将t条岭迹画出函数图像，当t条岭迹都大体处于稳定且没有不合理的符号时，这个状态下的值即可作为k值[14]。利用岭迹法选择k值的优点是应用方便，但具有随意性，容易造成较大误差。

3.2 双h法

由于岭迹法选取k值时具有较强的主观性，误差较大，还可根据双h法确定岭参数k。双h法如式(6)：

(6)

因为该公式中有2个可供选择的参数h1和h2，故称为双h法，当取G=I,h1=t,h2=0，上式就变为：

(7)

4案例分析

以唐山市华北理工大学曹妃甸校区实测数据为例。华北理工大学曹妃甸校区的高程系统为1984国家高程基准。测区实验点分布图如图1所示。

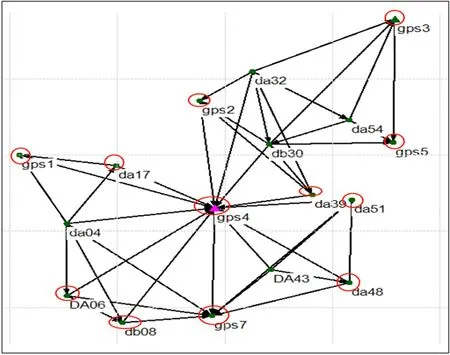
图1 测区实验点点位分布图

为减小实验误差，选取测区内gps1、gps2、gps3、gps4、gps5、gps7、da17、da06、da08、da48、da51、da39这12个GPS水准点作为已知点进行多项式拟合，其余da04、da30、da32、da43、da54这5个作为检核点。由于数据保密需要，对数据进行处理，部分实验数据如表1所示。

表1 测区实验点点位数据

考虑到不同多项式对曲面拟合的影响，利用matlab软件进行程序设计时，将已知点数据分别进行二次多项式拟合和三次多项式拟合。在进行精度评价时，采用最多的是内符合精度和外符合精度。内符合精度一般用μ表示，是根据参与拟合计算的已知点的高程异常值与实际得到的拟合值的差值V，以及拟合点的个数n，由公式(8)计算得到[15]。

(8)

外符合精度一般用M表示，是根据检核点的实测高程异常值与拟合得到的高程异常值的差值，以及检核点的个数m，由公式(9)计算得到。根据内符合精度和外符合精度可以评价模型的优劣[16]。

(9)

实验中，选取分布合理的12个点作为已知点来拟合似大地水准面模型，剩余5个点作为检核点。其中，二次多项式拟合和三次多项式拟合的条件数分别为6.231 4 e+21和6.232 3 e+21，说明法方程系数阵呈严重病态性，则采用岭估计的方法对其进行优化，不同拟合方法的精度如表2所示。

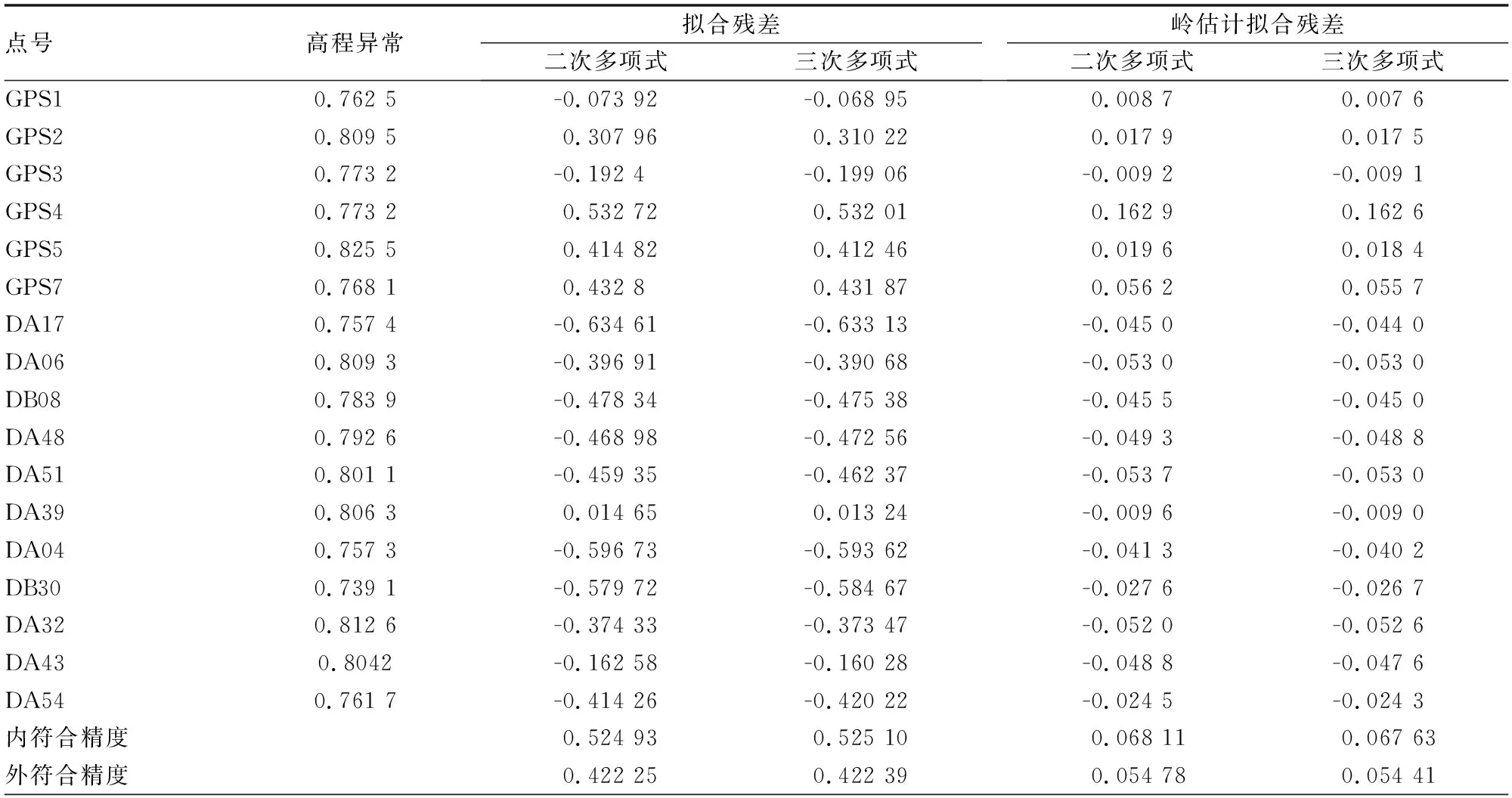
表2 不同拟合方法精度分析/m

由表2可以看出，采用二次多项式拟合得到的残差最大值为-0.634 61 m，最小残差为0.014 65 m；三次多项式拟合的残差最大值为-0.633 13 m，最小残差值为0.013 24 m；岭估计二次拟合中，最大残差值为0.162 9 m，最小残差值为0.008 7 m；采用岭估计三次拟合方法，得到的最大残差值为0.162 6 m，最小残差值为0.007 6 m。多项式曲面拟合方法由于方法简单，其模型应用最广，但其精度偏低，无论是二次多项式拟合还是三次多项式拟合，其拟合效果并不理想。其中，二次多项式内外符合精度分别为0.524 93 m和0.422 25 m，三次多项式拟合的内外符合精度分别为0.525 10 m和0.422 39 m。采用岭估计的方法进行高程拟合，精度明显得到了改善，其中岭估计二次拟合内外符合精度分别为0.068 11 m和0.054 78 m，岭估计三次拟合内外符合精度分别为0.067 63 m和0.054 41 m。

5结论

(1)在实例计算中，虽然测区内的实测点数量有限，但选取实验点位相对合理，在此基础上进行多项式拟合和岭估计可减少实验点位选取不合理带来的误差，但由于高程异常受多种因素影响，再加上实验数据有限，模型误差不可避免。

(2)由实验结果可以看出，多项式拟合模型简单，应用方便，但其系数矩阵的复共线性较强，无论是二次多项式拟合还是三次多项式拟合，其拟合精度并不能达到实际水准测量的要求。

(3)利用双h法选取岭参数k进行岭估计运算，能够很好改善最小二乘法下的多项式拟合，并且可以提高模型的内外符合精度，且效果显著，可达到实际测量要求的精度，实现对似大地水准面的精化。