葡萄酒差异性评价和可信度问题研究分析

周雪婷 刘禹辰

摘要：葡萄酒的之间的差异性有很多判别方法，本文比较两组评酒员的评价结果有无显著性差异，并建立合理的评价模型来判断两组结果在可信度方面的优劣。选取适用于小样本的Shapiro-wilk检验、直方图、正态Q-Q图进行正态分布验证，发现四组全部符合正态分布;采用T检验，检查两组评分均值是否存在显著性差异，通过比较p值与标准差，来评定可信度高的组别。

关键词：Shapiro-wilk检验;T检验;多元统计分析;葡萄酒;差异评价

一、数据预处理

由于给出的数据是自行测得的，可能会存在操作失误进而测错或者漏测、少测的情况发生。经过对数据的浏览分析，发现有些数据存在缺失，并且部分数据存在异常。因此，需要进行异常数据的修正和缺失数据的增添，这样才能确保实验数据和实验结果的正确性。

评酒员7对样品3口感持久性评分的数据，相较于相邻各评酒员的评分发生了明显的突变现象。这种数据异常可能对数据分析的结果产生不利影响。因此，采用求取平均值的方法进行修补。

同时，观察各组红葡萄酒各样品得分数据散点图，可以直觀的看到评酒员4对样品20的评分数据中，没有色调特征的数据，所以存在数据缺失情况。这种数据缺失可能会对后续模型建立、问题分析产生不利影响。因此，采用求取平均值的方法进行修补。

修改后的数据，可以很好的满足后续实验的需求，极大增高实验结果的稳定性。

二、评分的正态分布检验

对两组评酒员评分的差异性评价分析要求样本数据满足正态分布。因此，我们首先对样本数据的正态分布进行检验。此处我们对两组评分的均值数据进行检验，查看是否符合正态分布。

主要步骤如下所示：

Step1：统计每个酒样品评酒员的评分均值

首先，计算每一个酒样品的10名评酒员的评分均值，均值的公式如下所示：

（1）

其中，为缺失值，m为酒样品的组号。

Step2：进行Shapiro-wilk检验

由题意得，第一组红葡萄酒、第一组白葡萄酒、第二组红葡萄和第二组白葡萄样品的酒样品数目分别为27、28、27、28。所以，采用适用于小范围的Shapiro-wilk检验对样本进行检验，并绘制Q-Q图。

假设H0表示该组均值服从正态分布，H1表示该组均值不服从正态分布。

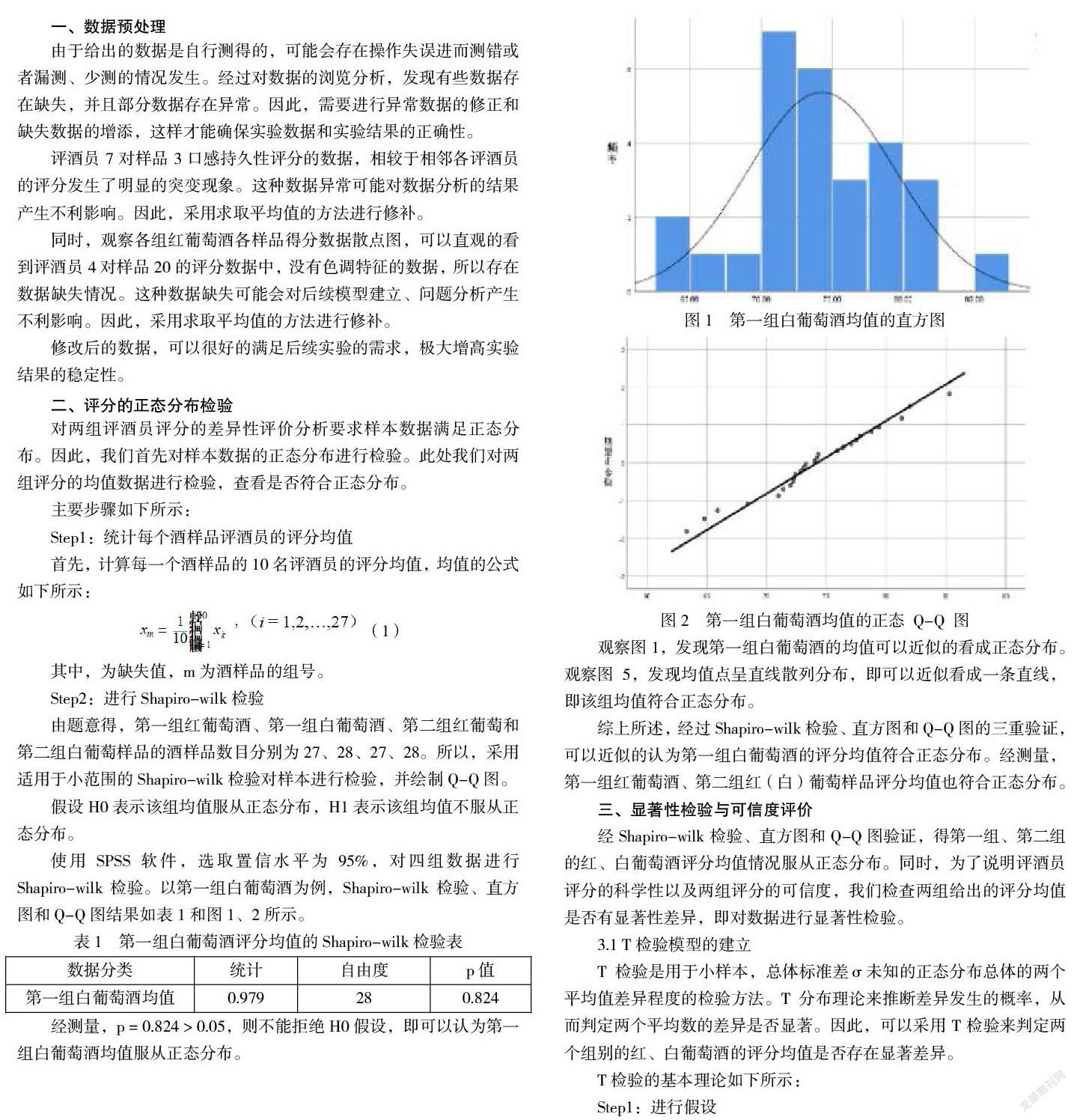
使用SPSS软件，选取置信水平为95%，对四组数据进行Shapiro-wilk检验。以第一组白葡萄酒为例，Shapiro-wilk检验、直方图和Q-Q图结果如表1和图1、2所示。

经测量，p = 0.824 > 0.05，则不能拒绝H0假设，即可以认为第一组白葡萄酒均值服从正态分布。

观察图1，发现第一组白葡萄酒的均值可以近似的看成正态分布。观察图5，发现均值点呈直线散列分布，即可以近似看成一条直线，即该组均值符合正态分布。

综上所述，经过Shapiro-wilk检验、直方图和Q-Q图的三重验证，可以近似的认为第一组白葡萄酒的评分均值符合正态分布。经测量，第一组红葡萄酒、第二组红（白）葡萄样品评分均值也符合正态分布。

三、显著性检验与可信度评价

经Shapiro-wilk检验、直方图和Q-Q图验证，得第一组、第二组的红、白葡萄酒评分均值情况服从正态分布。同时，为了说明评酒员评分的科学性以及两组评分的可信度，我们检查两组给出的评分均值是否有显著性差异，即对数据进行显著性检验。

3.1 T检验模型的建立

T检验是用于小样本，总体标准差σ未知的正态分布总体的两个平均值差异程度的检验方法。T分布理论来推断差异发生的概率，从而判定两个平均数的差异是否显著。因此，可以采用T检验来判定两个组别的红、白葡萄酒的评分均值是否存在显著差异。

T检验的基本理论如下所示：

Step1：进行假设

设 X1，X2，…，Xn1是来自总体N（ μ1，σ12 ） 的第一组酒样品评分均值，Y1，Y2，…，Yn2是来自总体 N（μ2，σ22） 的第二组酒样品评分均值，且两组酒样品的评分均值相互独立。为检验两个总体的均值是否有显著差异，给出假设：

3.2 T检验的进行

3.2.1 红葡萄可信度的评定

使用SPSS软件进行独立样本的T检验，得到T检验分析结果如表2、表3所示：

分析表2、表3可知：

莱文方差等同性检验结果为 F = 2.245，显著性概率为0.140>5%，因此，接收假设H0，认为两组评酒员对酒样品的评价结果无显著性关系。

第一组数据的标准差6.76255>第二组的标准差3.97799，标准误差平均值第一组1.30145>第二组0.76556，因此，第二组的评分更加稳定，数据的波动小。

因此，针对红葡萄酒而言，可认为第二组的评价结果更可信。

3.2.2 白葡萄可信度的评定

使用SPSS软件进行独立样本的T检验，得到的T检验分析结果如表4、表5所示：

分析表4、表5可知：

莱文方差等同性检验结果为 F = 5.044，显著性概率为 0.044 <5%，因此，接收假设H1，认为两组评酒员对酒样品的评价结果有显著性关系。

可以看出第一组数据的标准差5.20123>第二组的标准差3.17094，标准误差平均值第一组0.98294>第二组0.59925，因此，第二组的评分更加稳定，数据的波动小。

因此，针对白葡萄酒而言，可认为第二组的评价结果更可信。

综上，两组评酒员对于红葡萄酒评价没有显著差异，对白葡萄酒评价有显著差异，第二组的结果更可信。

四、综合评价

葡萄酒的之间的差异性有很多判别方法，本文比较两组评酒员的评价结果有无显著性差异，并建立合理的评价模型来判断两组结果在可信度方面的优劣。首先，进行数据预处理，完成异常数据的修改和缺失数据的增添;然后，选取适用于小样本的Shapiro-wilk检验、直方图、正态Q-Q图进行正态分布验证，发现四组全部符合正态分布;最后，采用T检验，检查两组评分均值是否存在显著性差异，通过比较p值与标准差，来评定可信度高的组别。实验发现两组评酒员对于红葡萄酒的评价没有显著性差异，对白葡萄酒的评价存在显著性差异，可第二组的标准差及标准误差平均值均小于第一组，因此，认为第二组更加可信。

参考文献：

[1]李猛.红葡萄酒品质特点及鉴别方法分析[J].中国果菜，2020，40（09）：65-68.

[2]田伟业，杨和财，张军翔，李甲贵，房玉林，陶永胜.中外葡萄酒产品等级分级评价及启示[J].中国酿造，2020，39（10）：220-224.

[3]陈虹瑶，杨易，季俊霖，徐绍荣，杨晓杰，潘立臣.基于AHP的葡萄酒产业发展影响因素评价[J].酿酒科技，2020（07）：124-128.

第一作者：周雪婷 女 汉 共青团员 本科 河南省郑州人  河南大学金融数学专业 方向：用数学方法与思维解决经济问题。

第二作者：作者简介：刘禹辰（2001—），女，汉，河南省郑州市人，学生，工学本科，河南师范大学计算机与信息工程学院，研究方向：数据分析和数据挖掘。